2.5: Polígonos de frecuencia
- Page ID
- 152186
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Crear e interpretar polígonos de frecuencia
- Crear e interpretar polígonos de frecuencia acumulativos
- Crear e interpretar polígonos de frecuencia superpuestos
Los polígonos de frecuencia son un dispositivo gráfico para comprender las formas de las distribuciones. Sirven para el mismo propósito que los histogramas, pero son especialmente útiles para comparar conjuntos de datos. Los polígonos de frecuencia también son una buena opción para mostrar distribuciones de frecuencia acumulativas.
Para crear un polígono de frecuencia, comience igual que para los histogramas, eligiendo un intervalo de clase. Luego dibuja un\(X\)-axis representing the values of the scores in your data. Mark the middle of each class interval with a tick mark, and label it with the middle value represented by the class. Draw the \(Y\)-axis to indicate the frequency of each class. Place a point in the middle of each class interval at the height corresponding to its frequency. Finally, connect the points. You should include one class interval below the lowest value in your data and one above the highest value. The graph will then touch the \(X\)-axis on both sides.
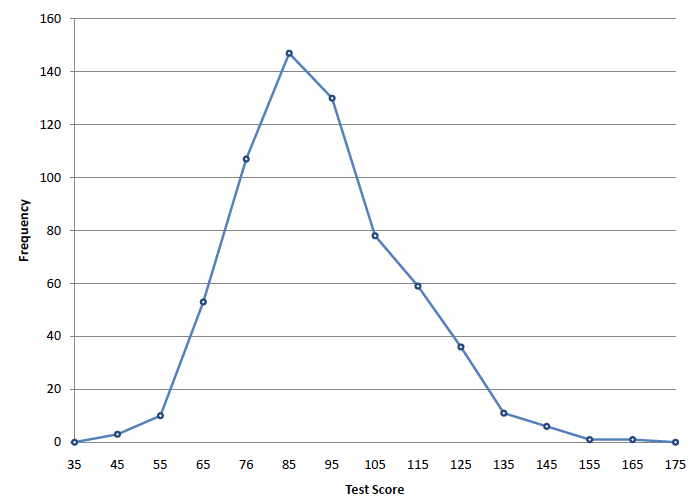
Se construyó un polígono de frecuencia para las puntuaciones de las pruebas de\(642\) psicología mostradas en la Figura\(\PageIndex{1}\) a partir de la tabla de frecuencias que se muestra en\(\PageIndex{1}\)
| Límite Inferior | Límite superior | Contar | Recuento Acumulado |
|---|---|---|---|
| 29.5 | 39.5 | 0 | 0 |
| 39.5 | 49.5 | 3 | 3 |
| 49.5 | 59.5 | 10 | 13 |
| 59.5 | 69.5 | 53 | 66 |
| 69.5 | 79.5 | 107 | 173 |
| 79.5 | 89.5 | 147 | 320 |
| 89.5 | 99.5 | 130 | 450 |
| 99.5 | 109.5 | 78 | 528 |
| 109.5 | 119.5 | 59 | 587 |
| 119.5 | 129.5 | 36 | 623 |
| 129.5 | 139.5 | 11 | 634 |
| 139.5 | 149.5 | 6 | 640 |
| 149.5 | 159.5 | 1 | 641 |
| 159.5 | 169.5 | 1 | 642 |
| 169.5 | 179.5 | 0 | 642 |
La primera etiqueta en el\(X\) eje es\(35\). Esto representa un intervalo que se extiende de\(29.5\) a\(39.5\). Dado que la puntuación más baja de la prueba es\(46\), este intervalo tiene una frecuencia de\(0\). El punto etiquetado\(45\) representa el intervalo de\(39.5\) a\(49.5\). Hay tres puntuaciones en este intervalo. Hay\(147\) puntuaciones en el intervalo que rodea\(85\).
Se puede discernir fácilmente la forma de la distribución a partir de Figura\(\PageIndex{1}\). La mayoría de los puntajes están entre\(65\) y\(115\). Es claro que la distribución no es simétrica en la medida en que las buenas puntuaciones (a la derecha) se desfilan más gradualmente que las malas puntuaciones (a la izquierda). En la terminología del Capítulo 3 (donde estudiaremos formas de distribuciones de manera más sistemática), la distribución es sesgada.
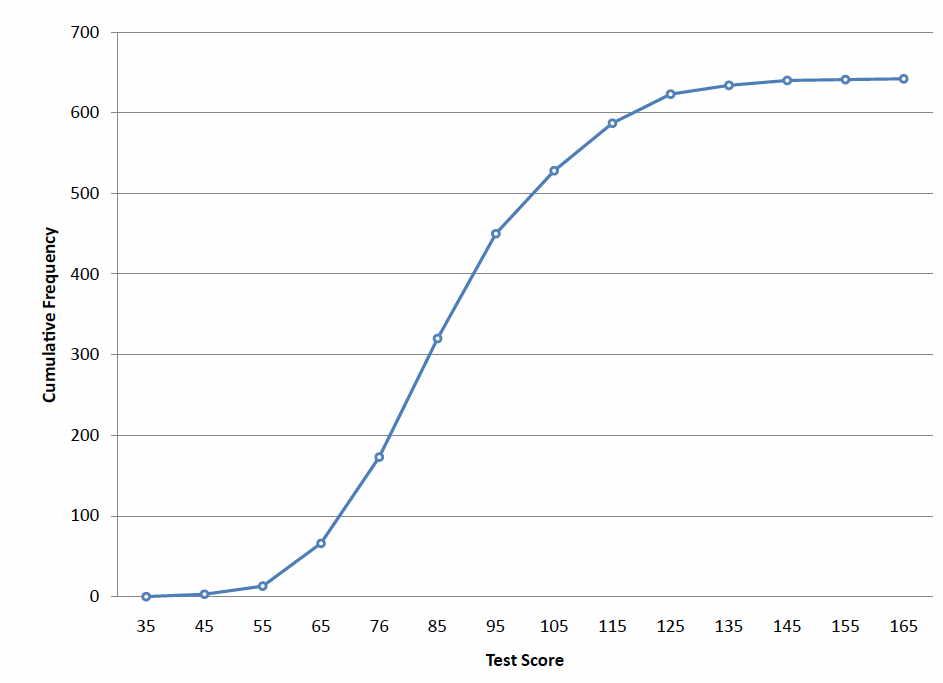
En la Figura se muestra un polígono de frecuencia acumulativa para las mismas puntuaciones de prueba\(\PageIndex{2}\). La gráfica es la misma que antes excepto que el\(Y\) valor para cada punto es el número de alumnos en el intervalo de clase correspondiente más todos los números en intervalos inferiores. Por ejemplo, no hay puntuaciones en el intervalo etiquetado\(35\), tres en el intervalo\(45\) y\(10\) en el intervalo\(55\). Por lo tanto, el\(Y\) valor correspondiente a "\(55\)" es\(13\). Desde que\(642\) los estudiantes tomaron la prueba, la frecuencia acumulada para el último intervalo es\(642\).
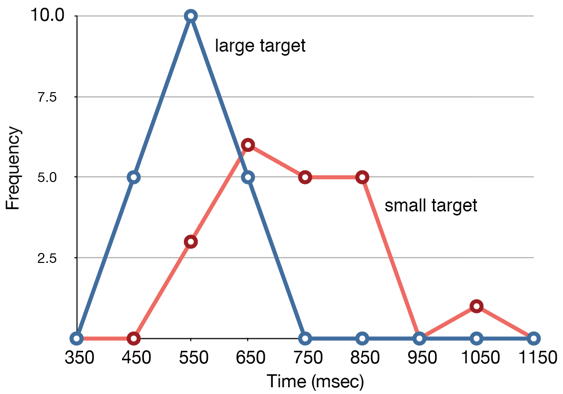
Los polígonos de frecuencia son útiles para comparar distribuciones. Esto se logra superponiendo los polígonos de frecuencia dibujados para diferentes conjuntos de datos. La figura\(\PageIndex{3}\) proporciona un ejemplo. Los datos provienen de una tarea en la que el objetivo es mover un cursor de computadora a un objetivo en la pantalla lo más rápido posible. En\(20\) de los ensayos, el objetivo era un rectángulo pequeño; en el otro\(20\), el objetivo era un rectángulo grande. En cada ensayo se registró el tiempo para alcanzar el objetivo. Las dos distribuciones (una para cada objetivo) se trazan juntas en la Figura\(\PageIndex{3}\). La figura muestra que, aunque hay cierta superposición en los tiempos, generalmente tardó más tiempo en mover el cursor al objetivo pequeño que al grande.
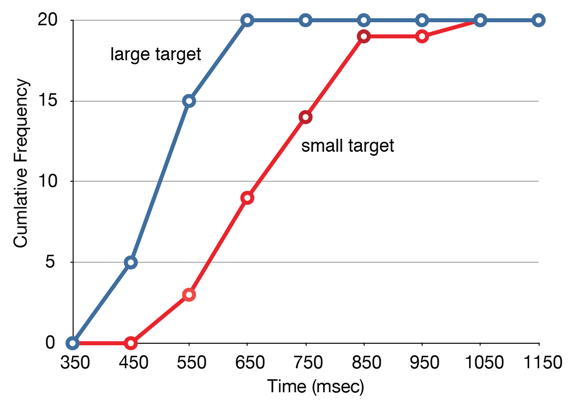
También es posible trazar dos distribuciones de frecuencia acumuladas en una misma gráfica. Esto se ilustra en la Figura\(\PageIndex{4}\) usando los mismos datos de la tarea del cursor. La diferencia en las distribuciones para los dos objetivos vuelve a ser evidente.


