6.2: La distribución muestral de la media muestral
- Page ID
- 151183
Objetivos de aprendizaje
- Conocer cuál\(\overline{X}\) es la distribución muestral cuando el tamaño de la muestra es grande.
- Conocer cuál\(\overline{X}\) es la distribución muestral cuando la población es normal.
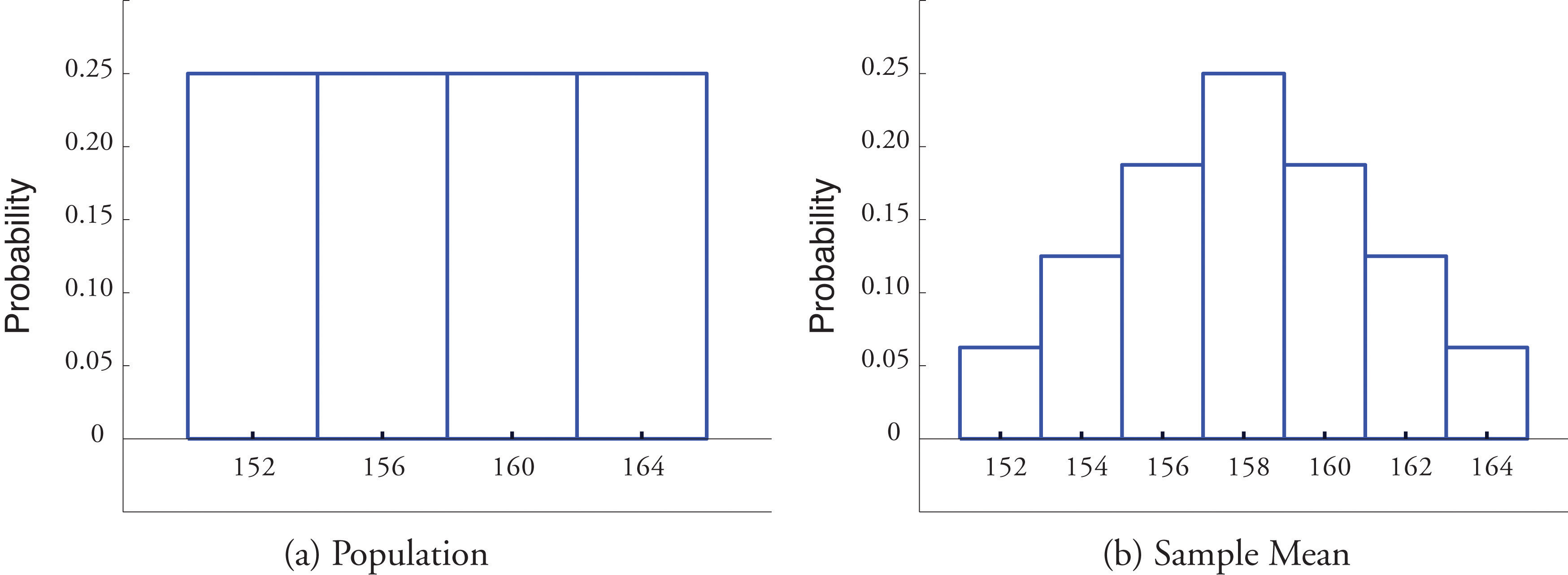
En el Ejemplo 6.1.1, se construyó la distribución de probabilidad de la media muestral para muestras de tamaño dos extraídas de la población de cuatro remeros. La distribución de probabilidad es:
\[\begin{array}{c|c c c c c c c} \bar{x} & 152 & 154 & 156 & 158 & 160 & 162 & 164\\ \hline P(\bar{x}) &\dfrac{1}{16} &\dfrac{2}{16} &\dfrac{3}{16} &\dfrac{4}{16} &\dfrac{3}{16} &\dfrac{2}{16} &\dfrac{1}{16}\\ \end{array}\]
La figura\(\PageIndex{1}\) muestra una comparación lado a lado de un histograma para la población original y un histograma para esta distribución. Mientras que la distribución de la población es uniforme, la distribución muestral de la media tiene una forma que se aproxima a la forma de la curva de campana familiar. Este fenómeno de la distribución muestral de la media tomando forma de campana a pesar de que la distribución poblacional no es en forma de campana ocurre en general. Aquí hay un ejemplo algo más realista.
Supongamos que tomamos muestras de tamaño\(1\)\(5\),\(10\), o\(20\) de una población que consiste enteramente en los números\(0\) y\(1\), la mitad de la población\(0\), la mitad\(1\), para que la media poblacional sea\(0.5\). Las distribuciones de muestreo son:
\(n = 1\):
\[\begin{array}{c|c c } \bar{x} & 0 & 1 \\ \hline P(\bar{x}) &0.5 &0.5 \\ \end{array} \nonumber\]
\(n = 5\):
\[\begin{array}{c|c c c c c c} \bar{x} & 0 & 0.2 & 0.4 & 0.6 & 0.8 & 1 \\ \hline P(\bar{x}) &0.03 &0.16 &0.31 &0.31 &0.16 &0.03 \\ \end{array} \nonumber\]
\(n = 10\):
\[\begin{array}{c|c c c c c c c c c c c} \bar{x} & 0 & 0.1 & 0.2 & 0.3 & 0.4 & 0.5 & 0.6 & 0.7 & 0.8 & 0.9 & 1 \\ \hline P(\bar{x}) &0.00 &0.01 &0.04 &0.12 &0.21 &0.25 &0.21 &0.12 &0.04 &0.01 &0.00 \\ \end{array} \nonumber\]
\(n = 20\):
\[\begin{array}{c|c c c c c c c c c c c} \bar{x} & 0 & 0.05 & 0.10 & 0.15 & 0.20 & 0.25 & 0.30 & 0.35 & 0.40 & 0.45 & 0.50 \\ \hline P(\bar{x}) &0.00 &0.00 &0.00 &0.00 &0.00 &0.01 &0.04 &0.07 &0.12 &0.16 &0.18 \\ \end{array} \nonumber\]
y
\[\begin{array}{c|c c c c c c c c c c } \bar{x} & 0.55 & 0.60 & 0.65 & 0.70 & 0.75 & 0.80 & 0.85 & 0.90 & 0.95 & 1 \\ \hline P(\bar{x}) &0.16 &0.12 &0.07 &0.04 &0.01 &0.00 &0.00 &0.00 &0.00 &0.00 \\ \end{array} \nonumber\]
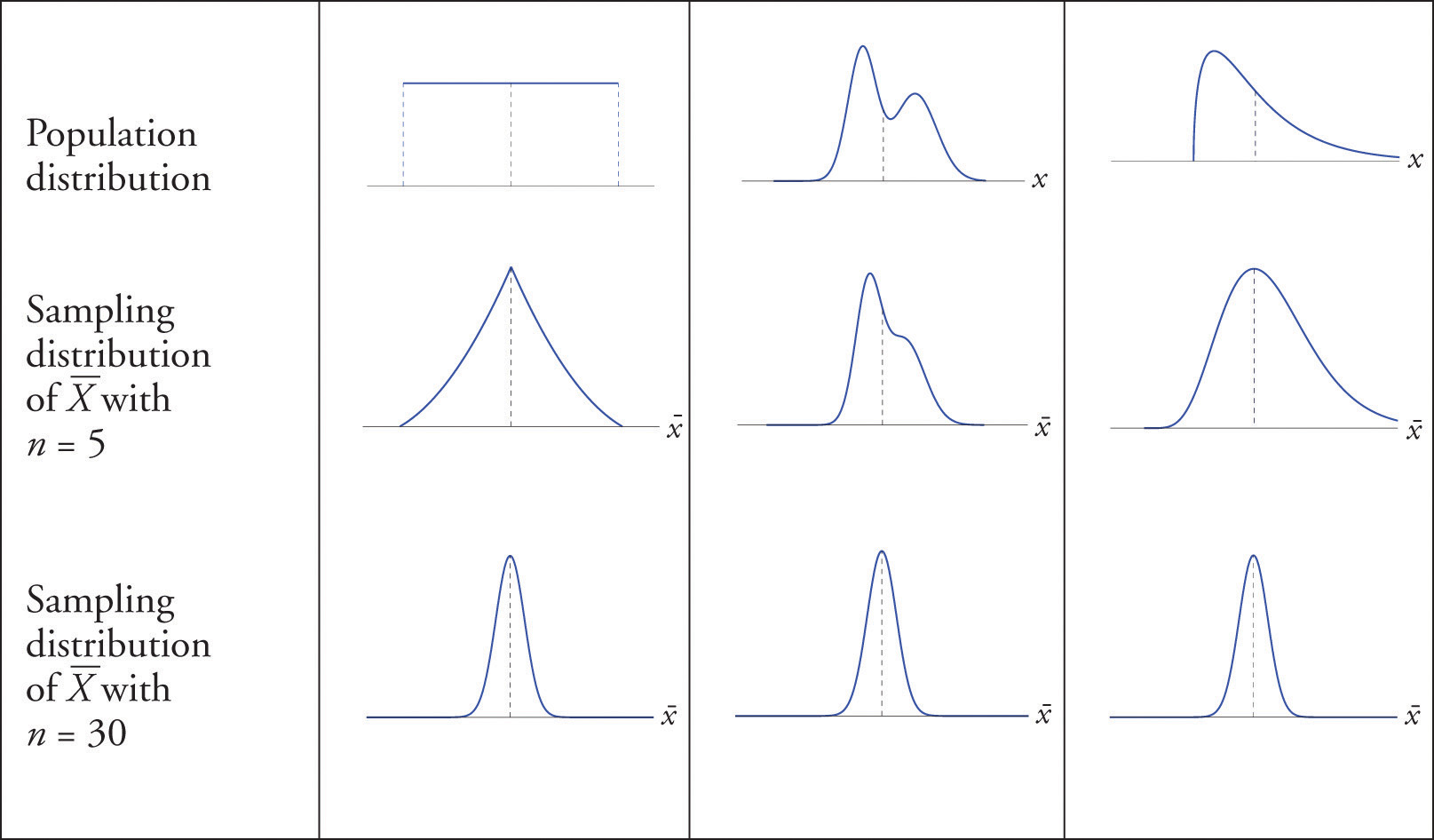
Los histogramas que ilustran estas distribuciones se muestran en la Figura\(\PageIndex{2}\).

A\(n\) medida que aumenta la distribución muestral de\(\overline{X}\) evoluciones de una manera interesante: las probabilidades en los extremos inferior y superior se contraen y las probabilidades en el medio se hacen mayores en relación con ellas. Si continuáramos aumentando\(n\) entonces la forma de la distribución del muestreo se volvería más suave y en forma de campana.
Lo que estamos viendo en estos ejemplos no depende de las distribuciones poblacionales particulares involucradas. En general, se puede comenzar con cualquier distribución y la distribución de muestreo de la media muestral se asemejará cada vez más a la curva normal en forma de campana a medida que aumenta el tamaño de la muestra. Este es el contenido del Teorema del Límite Central.
El Teorema del Límite Central
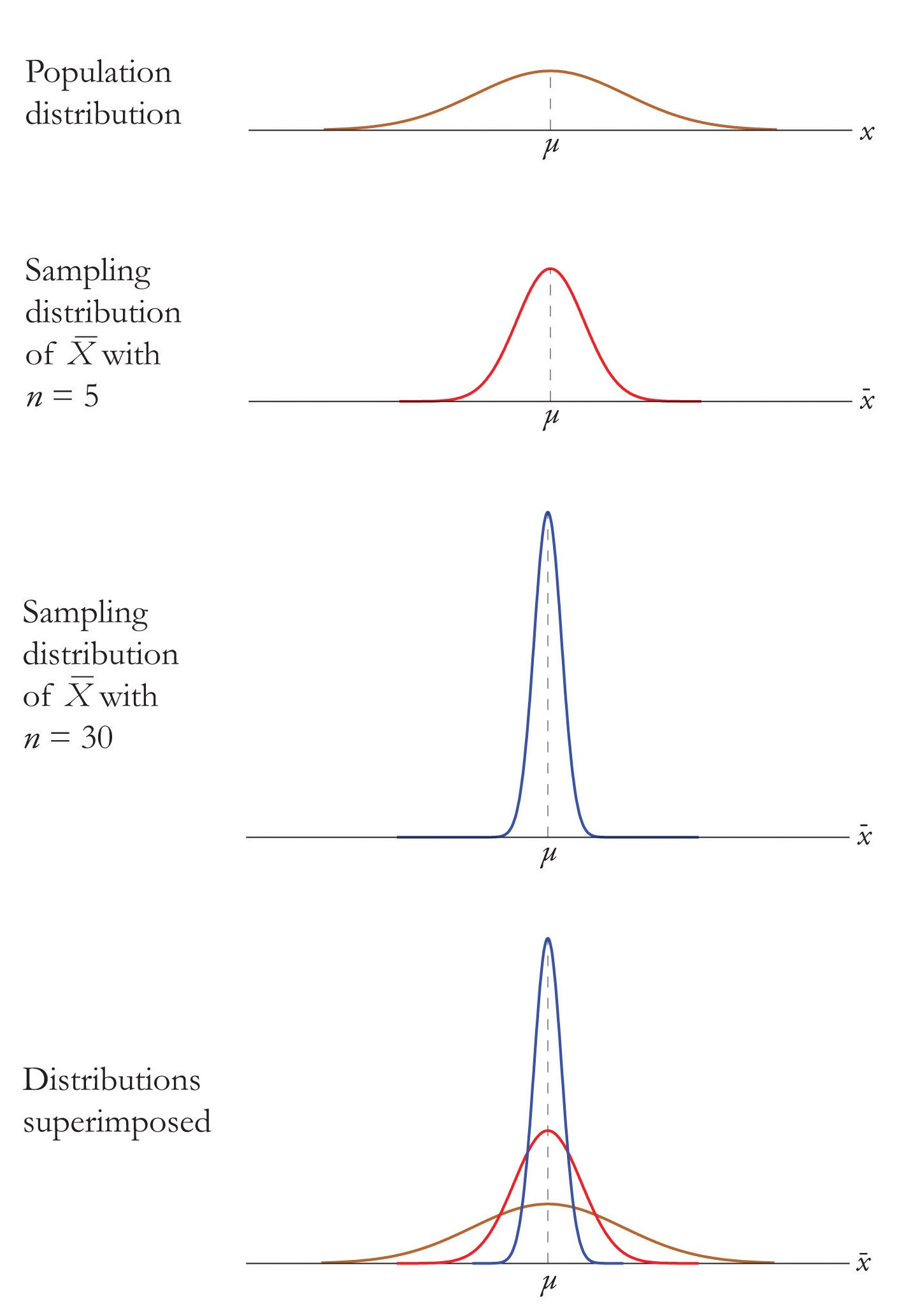
Para muestras de tamaño\(30\) o más, la media de la muestra se distribuye aproximadamente normalmente, con media\(\mu _{\overline{X}}=\mu\) y desviación estándar\(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}\), donde\(n\) está el tamaño de la muestra. Cuanto mayor sea el tamaño de la muestra, mejor será la aproximación. El Teorema del Límite Central se ilustra para varias distribuciones poblacionales comunes en la Figura\(\PageIndex{3}\).
Las líneas verticales discontinuas en las figuras localizan la media poblacional. Independientemente de la distribución de la población, a medida que aumenta el tamaño de la muestra, la forma de la distribución muestral de la media muestral se vuelve cada vez más en forma de campana, centrada en la media poblacional. Típicamente para cuando el tamaño de la muestra es\(30\) la distribución de la media de la muestra es prácticamente la misma que una distribución normal.
La importancia del Teorema del Límite Central es que nos permite hacer declaraciones de probabilidad sobre la media muestral, específicamente en relación a su valor en comparación con la media poblacional, como veremos en los ejemplos. Pero para usar correctamente el resultado primero debemos darnos cuenta de que hay dos variables aleatorias separadas (y por lo tanto dos distribuciones de probabilidad) en juego:
- \(X\), la medición de un solo elemento seleccionado al azar de la población; la distribución de\(X\) es la distribución de la población, con media la media de la población\(\mu\) y desviación estándar la desviación estándar de la población\(\sigma\);
- \(\overline{X}\), la media de las mediciones en una muestra de tamaño\(n\); la distribución de\(\overline{X}\) es su distribución muestral, con media\(\mu _{\overline{X}}=\mu\) y desviación estándar\(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}\).
Ejemplo\(\PageIndex{1}\)
\(\overline{X}\)Sea la media de una muestra aleatoria de tamaño\(50\) extraída de una población con media\(112\) y desviación estándar\(40\).
- Encuentra la media y desviación estándar de\(\overline{X}\).
- Encuentra la probabilidad que\(\overline{X}\) asume un valor entre\(110\) y\(114\).
- Encuentra la probabilidad de que\(\overline{X}\) asuma un valor mayor que\(113\).
Solución:
- Por las fórmulas de la sección anterior\[\mu _{\overline{X}}=\mu=112 \nonumber\] y\[ \sigma_{\overline{X}}=\dfrac{\sigma}{\sqrt{n}}=\dfrac{40} {\sqrt{50}}=5.65685 \nonumber\]
- Dado que el tamaño de la muestra es al menos\(30\), se aplica el Teorema del Límite Central:\(\overline{X}\) se distribuye aproximadamente normalmente. Calculamos probabilidades usando la Figura 5.3.1 de la manera habitual, solo teniendo cuidado de usar\(\sigma _{\overline{X}}\) y no\(\sigma\) cuando estandarizamos:
\[\begin{align*} P(110<\overline{X}<114)&= P\left ( \dfrac{110-\mu _{\overline{X}}}{\sigma _{\overline{X}}} <Z<\dfrac{114-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( \dfrac{110-112}{5.65685} <Z<\dfrac{114-112}{5.65685}\right )\\[4pt] &= P(-0.35<Z<0.35)\\[4pt] &= 0.6368-0.3632\\[4pt] &= 0.2736 \end{align*}\]
- Del mismo modo
\[\begin{align*} P(\overline{X}> 113)&= P\left ( Z>\dfrac{113-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z>\dfrac{113-112}{5.65685}\right )\\[4pt] &= P(Z>0.18)\\[4pt] &= 1-P(Z<0.18)\\[4pt] &= 1-0.5714\\[4pt] &= 0.4286 \end{align*}\]
Obsérvese que si en el ejemplo anterior nos hubieran pedido calcular la probabilidad de que el valor de un solo elemento seleccionado aleatoriamente de la población supere\(113\), es decir\(P(X>113)\), para calcular el número, no hubiéramos podido hacerlo, ya que no conocemos la distribución de\(X\), sino sólo que su media es\(112\) y su desviación estándar es\(40\). Por el contrario, podríamos calcular\(P(\overline{X}>113)\) incluso sin un conocimiento completo de la distribución de\(X\) porque el Teorema del Límite Central garantiza que\(\overline{X}\) es aproximadamente normal.
Ejemplo\(\PageIndex{2}\)
La población numérica de promedios de grado en una universidad tiene media\(2.61\) y desviación estándar\(0.5\). Si\(100\) se toma una muestra aleatoria de tamaño de la población, ¿cuál es la probabilidad de que la media de la muestra esté entre\(2.51\) y\(2.71\)?
Solución:
La media muestral\(\overline{X}\) tiene media\(\mu _{\overline{X}}=\mu =2.61\) y desviación estándar\(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{0.5}{10}=0.05\), por lo que
\[\begin{align*} P(2.51<\overline{X}<2.71)&= P\left ( \dfrac{2.51-\mu _{\overline{X}}}{\sigma _{\overline{X}}} <Z<\dfrac{2.71-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( \dfrac{2.51-2.61}{0.05} <Z<\dfrac{2.71-2.61}{0.05}\right )\\[4pt] &= P(-2<Z<2)\\[4pt] &= P(Z<2)-P(Z<-2)\\[4pt] &= 0.9772-0.0228\\[4pt] &= 0.9544 \end{align*}\]
Poblaciones normalmente distribuidas
El Teorema del Límite Central dice que no importa cuál sea la distribución de la población, siempre y cuando la muestra sea “grande”, significado de tamaño\(30\) o más, la media de la muestra se distribuye aproximadamente normalmente. Si la población es normal para empezar entonces la media muestral también tiene una distribución normal, independientemente del tamaño de la muestra.
Para muestras de cualquier tamaño extraídas de una población normalmente distribuida, la media muestral se distribuye normalmente, con media\(μ_X=μ\) y desviación estándar\(σ_X =σ/\sqrt{n}\), donde\(n\) está el tamaño de la muestra.
El efecto de aumentar el tamaño de la muestra se muestra en la Figura\(\PageIndex{4}\).
Ejemplo\(\PageIndex{3}\)
Un prototipo de neumático automotriz tiene una vida útil de diseño de\(38,500\) millas con una desviación estándar de\(2,500\) millas. Cinco de esas llantas son fabricadas y probadas. En el supuesto de que la media poblacional real es\(38,500\) millas y la desviación estándar de la población real es\(2,500\) millas, encuentre la probabilidad de que la media de la muestra sea menor que\(36,000\) millas. Supongamos que la distribución de los tiempos de vida de dichas llantas es normal.
Solución:
Para simplificar utilizamos unidades de miles de millas. Entonces la media muestral\(\overline{X}\) tiene media\(\mu _{\overline{X}}=\mu =38.5\) y desviación estándar\(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{2.5}{\sqrt{5}}=1.11803\). Dado que la población está normalmente distribuida, así es\(\overline{X}\), de ahí
\[\begin{align*} P(\overline{X}<36)&= P\left ( Z<\dfrac{36-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z<\dfrac{36-38.5}{1.11803}\right )\\[4pt] &= P(Z<-2.24)\\[4pt] &= 0.0125 \end{align*}\]
Es decir, si las llantas funcionan como están diseñadas, solo hay una\(1.25\%\) posibilidad de que el promedio de una muestra de este tamaño sea tan bajo.
Ejemplo\(\PageIndex{4}\)
Un fabricante de baterías para automóviles afirma que su batería de grado medio tiene una vida media de\(50\) meses con una desviación estándar de\(6\) meses. Supongamos que la distribución de la duración de las baterías de esta marca en particular es aproximadamente normal
- En el supuesto de que las afirmaciones del fabricante son ciertas, encuentre la probabilidad de que una batería seleccionada al azar de este tipo dure menos de\(48\) meses.
- En el mismo supuesto, encontrar la probabilidad de que la media de una muestra aleatoria de\(36\) tales baterías sea menor que\(48\) meses.
Solución:
- Dado que se sabe que la población tiene una distribución normal
\[\begin{align*} P(X<48)&= P\left ( Z<\dfrac{48-\mu }{\sigma }\right )\\[4pt] &= P\left ( Z<\dfrac{48-50}{6}\right )\\[4pt] &= P(Z<-0.33)\\[4pt] &= 0.3707 \end{align*}\]
- La media muestral tiene media\(\mu _{\overline{X}}=\mu =50\) y desviación estándar\(\sigma _{\overline{X}}=\dfrac{\sigma }{\sqrt{n}}=\dfrac{6}{\sqrt{36}}=1\). Así
\[\begin{align*} P(\overline{X}<48)&= P\left ( Z<\dfrac{48-\mu _{\overline{X}}}{\sigma _{\overline{X}}}\right )\\[4pt] &= P\left ( Z<\dfrac{48-50}{1}\right )\\[4pt] &= P(Z<-2)\\[4pt] &= 0.0228 \end{align*}\]
Llave para llevar
- Cuando el tamaño de la muestra es al menos\(30\) la media de la muestra se distribuye normalmente.
- Cuando la población es normal, la media muestral se distribuye normalmente independientemente del tamaño de la muestra.

