2.6: Óptica Geométrica Gaussiana
- Page ID
- 129990
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Hemos visto anteriormente que mediante el uso de lentes o espejos que tienen superficies que son secciones cónicas podemos imaginar perfectamente un cierto par de puntos, pero para otros puntos la imagen en general no es perfecta. Las imperfecciones son causadas por rayos que hacen ángulos mayores con el eje óptico, es decir, con el eje de simetría del sistema. Los rayos para los que estos ángulos son pequeños se denominan rayos paraxiales. Debido a que para los rayos paraxiales los ángulos de incidencia y transmisión en las superficies de las lentes son pequeños, el seno de los ángulos en la Ley de Snell se sustituye por los propios ángulos:
\[n_{i}θ_{i}=n_{t}θ_{t}. \tag{paraxial space rays space only} \]
Esta aproximación simplifica enormemente los cálculos. Cuando solo se consideran los rayos paraxiales, se puede reemplazar cualquier superficie refractaria por una esfera con la misma curvatura en su vértice. Para los rayos paraxiales, los errores causados al reemplazar la superficie general por una esfera son de segundo orden y por lo tanto insignificantes. Las superficies esféricas no sólo son más simples en las derivaciones sino que también son mucho más fáciles de fabricar. De ahí que en la industria óptica se utilicen mucho las superficies esféricas. Para reducir los errores de imagen causados por rayos no paraxiales se aplican dos estrategias:
- añadir más superficies esféricas
- reemplazando una de las superficies esféricas (típicamente la última antes del espacio de imagen) por una no-esfera.
En la óptica geométrica gaussiana solo se consideran los rayos paraxiales y las superficies esféricas. En la óptica geométrica gaussiana cada punto tiene una imagen perfecta.
2.5.1 Imágenes gaussianas por una sola superficie esférica
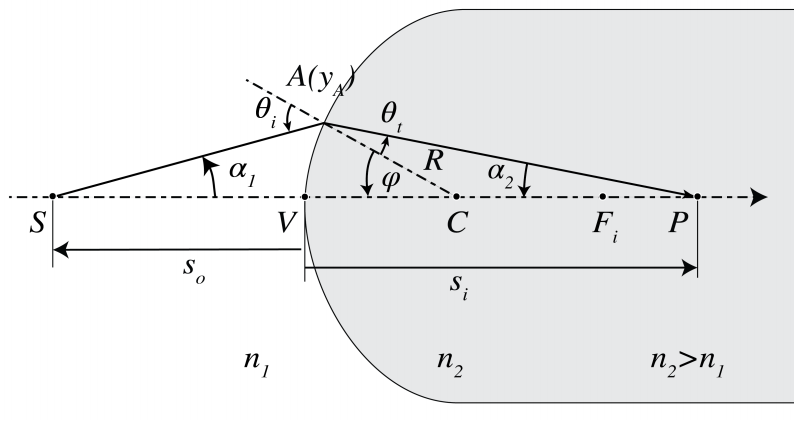
Primero mostraremos que dentro de la óptica gaussiana una sola superficie esférica entre dos medios con índices de refracción n 1 < n 2 imagina todos los puntos perfectamente (Figura\(\PageIndex{1}\)). La esfera tiene radio R y centro C que está dentro del medio 2. Consideramos un objeto puntual S a la izquierda de la superficie. Dibujamos un rayo desde S perpendicular a la superficie. El punto de intersección es V. Dado que para este rayo el ángulo de incidencia con la normal local en la superficie desaparece, el rayo continúa hacia el segundo medio sin refracción y pasa por el centro C de la esfera. A continuación dibujamos un rayo que golpea la superficie esférica en algún punto A y dibujamos el rayo refractado en el medio 2 usando la ley de Snell en la forma paraxial (\(\PageIndex{1}\)) (nótese que los ángulos de incidencia y transmisión deben medirse con respecto a la normal local en A, es decir, con respecto a CA). Suponemos que este rayo cruza el primer rayo en el punto P. Mostraremos que dentro de la aproximación de la óptica geométrica gaussiana, todos los rayos de S pasan a través de P. Además, con respecto a un sistema de coordenadas (y, z) con origen en V, el eje z apuntando de V a C y el eje y positivo hacia arriba como que se muestra en la Figura\(\PageIndex{1}\), tenemos:
\[-\dfrac{n_{1}}{s_{0}}+\dfrac{n_{2}}{s_{i}}=\dfrac{n_{2}-n_{1}}{R}. \nonumber \]
donde s 0 y s i son las coordenadas z- de S y P, respectivamente (de ahí s 0 0 < 0 and si > en la Figura\(\PageIndex{1}\)).
Prueba.
(Nota: el comprobante no forma parte del examen). Baste con mostrar que P es independiente del rayo, es decir de A. Esto lo haremos expresando s i en s o y mostrando que el resultado es independiente de A. Sea α 1 y α 2 los ángulos de los rayos SA y AP con el eje z como se muestra en la Figura\(\PageIndex{1}\). Sea θ i el ángulo de incidencia del rayo SA con la CA normal local en la superficie y θ t sea el ángulo de refracción. Al considerar los ángulos en ∆SCA encontramos
\[θ_{i}=α_{1}+ϕ. \nonumber \]
De igual manera, a partir de ∆CPA encontramos
\[θ_{t}=-α_{2}+ϕ. \nonumber \]
Por sustitución en la versión paraxial de la Ley de Snell (\(\PageIndex{1}\)), obtenemos
\[n_{1}α_{1}+n_{2}α_{2}=(n_{2}-n_{1})ϕ. \nonumber \]
Que y A y z A sean las coordenadas del punto A. Desde s o < 0 y s i > 0 tenemos
\[α_{1}≈tan(α_{1})=\dfrac{y_{A}}{z_{A}-s_{o}},α_{2}≈tan(α_{2})=\dfrac{y_{A}}{s_{i}-z_{A}}. \nonumber \]
Además,
\[ϕ≈\sin ϕ≈\dfrac{y_{A}}{R}. \nonumber \]
que es pequeño para los rayos paraxiales. Por lo tanto,
\[z_{A}=R-R\cos ϕ=R-R(1-\dfrac{ϕ^2}{2})=\dfrac{R}{2}ϕ^2≈0, \nonumber \]
porque es de segundo orden en y A y por lo tanto se descuida en la aproximación paraxial. Entonces, (\(\PageIndex{6}\)se convierte en
\[α_{1}=-\dfrac{y_{A}}{s_{o}},α_{2}=\dfrac{y_{A}}{s_{i}}. \nonumber \]
Al sustituir (\(\PageIndex{9}\)y (\(\PageIndex{7}\)en (\(\PageIndex{5}\)encontramos − (n 1 /s o) y A + (n 2 /z i) y A = [(n 2 − n 1) /R] y A, o −n 1 /s o +n 2 /z i =( n 2 − n 1) /R, que es la Ec. (\(\PageIndex{2}\). Implica que\(s_i\), y por lo tanto\(P\), es independiente de y A, es decir, del rayo elegido. Por lo tanto, P es una imagen perfecta dentro de la aproximación de la óptica geométrica gaussiana.
Cuando s i → ∞, el rayo después de la refracción es paralelo al eje z y obtenemos así → −n 1 R/ (n 2 − n 1). El punto objeto para el cual los rayos en el medio 2 son paralelos al eje z se denomina el primer punto focal o punto focal objeto F o, Su coordenada z es:
\[f_{o}=- \dfrac{ n_{1}R }{ n_{2} -n_{1} }. \nonumber \]
A pesar de que se trata de una coordenada y por lo tanto tiene un signo, también se le llama distancia focal frontal o distancia focal del objeto.
Cuando s o → −∞, el rayo incidente es paralelo al eje z en el medio 1 y el punto de imagen correspondiente Fi se denomina segundo punto focal o punto focal de imagen. Su coordenada z viene dada por:
\[f_{i}=\dfrac{ n_{2}R }{ n_{2} -n_{1} }, \nonumber \]
y también se le conoce como la segunda distancia focal o distancia focal de la imagen. Con (\(\PageIndex{11}\)) y (\(\PageIndex{10}\)), (\(\PageIndex{2}\)) se puede reescribir como:
\[- \dfrac{ n_{1}}{ s_{o} }+ \dfrac{ n_{2}}{ s_{i} } = \dfrac{ n_{2}}{ f_{i} } = -\dfrac{ n_{1}}{ f_{o} }. \nonumber \]
Al adoptar la convención de signos que figura en la Tabla\(\PageIndex{1}\) siguiente, resulta que (\(\PageIndex{2}\)) sostiene en general. Por ejemplo, cuando el punto S está entre el punto focal frontal y el vértice V de manera que f o < s o < 0, los rayos de S son tan fuertemente divergentes que la refracción es insuficiente para obtener un punto de imagen en medio 2. En cambio hay un haz de rayos divergentes en el medio 2 que para un observador en medio 2 parece provenir de un punto P en el medio 1 con la coordenada z si, de ahí si < 0, de acuerdo con el hecho de que P está ahora a la izquierda de V. El punto P se llama imagen virtual porque no corresponde a una concentración real de energía lumínica en el espacio. Cuando s i > 0 hay una concentración de energía luminosa en P que por lo tanto se denomina entonces imagen real.
| cantidad | positivo | negativo |
|---|---|---|
| s o, f o, s i, f i | el punto correspondiente está a la derecha del vértice | el punto correspondiente está a la izquierda del vértice |
| R | centro de curvatura a la derecha del vértice | centro de curvatura a la izquierda del vértice |
| α (ángulo de rayos astuto) | si la rotación en sentido antihorario sobre α hace que el rayo sea paralelo al eje z | si la rotación en sentido horario sobre α hace que el rayo sea paralelo al eje z |
| Índice refr. n medio ambiente del espejo | antes de la reflexión | después de la reflexión |
Si\(n_1 > n_2\) o\(R < 0\) (es decir, la superficie es cóncava cuando se ve desde la izquierda del vértice), el lado derecho de (\(\PageIndex{2}\)) es negativo:
\[\dfrac{n_{2}-n_{1}}{R}<0. \nonumber \]
Los rayos de luz que inciden desde la izquierda se refractan luego lejos del eje z y los rayos incidentes que son paralelos al eje z se refractan de tal manera que nunca se cruzan con el eje z en el medio 2. En cambio, parecen ser emitidos por un punto en medio 1. Como se ilustra en la Figura\(\PageIndex{2}\), el segundo punto focal es por lo tanto virtual con una distancia focal negativa dada por:
\[f_{i}=\dfrac{n_{2}R}{n_{2}-n_{1}}<0. \nonumber \]
Además, f o > 0 y un rayo incidente que después de la refracción es paralelo al eje z en el medio 2 parece que un observador en el medio 1 converja a un punto en el medio 2. De ahí que el primer punto focal también sea virtual: f o > 0. Cuando (\(\PageIndex{12}\)) se mantiene, para todos los puntos de objeto S delante de la lente (s o < 0), el punto de imagen es siempre virtual. De hecho, si dado por (\(\PageIndex{2}\)) es entonces siempre negativo.
2.5.2 Vectores de rayos y matrices de rayos
En óptica geométrica es conveniente utilizar vectores de rayos y matrices de rayos. En cualquier plano perpendicular al eje z, un rayo está determinado por la coordenada y del punto de intersección del rayo con el plano y el ángulo agudo α del rayo con el eje z. Aquí y > 0 cuando el punto de intersección está por encima del eje z e y < 0 en caso contrario. Definimos el vector de rayos
\[\dbinom{nα}{y}, \nonumber \]
donde n es el índice de refracción local. La definición con el índice de refracción como factor en el primer elemento del vector de rayos resulta conveniente. El ángulo agudo α tiene signo de acuerdo a la convención en la Tabla\(\PageIndex{1}\).
Los vectores de rayos de un rayo en dos planos cualesquiera z = z 1, z = z 2, con z 2 > z 1, están relacionados por una llamada matriz de rayos:
\[\dbinom{n_{2}α_{2}}{y_{2}}=M\dbinom{n_{1}α_{1}}{y_{1}}. \nonumber \]
donde
\[M=\begin{pmatrix} A & B \\ C & D \end{pmatrix}. \nonumber \]
Los elementos de la matriz M dependen de los componentes ópticos y materiales entre los planos z = z 1 y z = z 2.
Como ejemplo, considere la matriz de rayos que relaciona un vector de rayos en el plano inmediatamente anterior\(\PageIndex{2}\) a la superficie esférica en la Figura con el vector de rayos correspondiente en el plano inmediatamente detrás de esa superficie. Usando (\(\PageIndex{5}\)) y (\(\PageIndex{7}\)) sigue
\[n_{1}α_{1}-n_{2}α_{2}=\dfrac{(n_{2}-n_{1})y_{1}}{R}, \nonumber \]
donde hemos reemplazado α 2 por −α 2 in (\(\PageIndex{5}\)), porque de acuerdo con la convención de signos, el ángulo α 2 en la Figura\(\PageIndex{1}\) debe tomarse negativo. Porque además y 2 = y 1, concluimos
\[\dbinom{n_{2}α_{2}}{y_{2}}=\dbinom{n_{1}α_{1}-\dfrac{(n_{2}-n_{1})y_{1}}{R}}{y_{1}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space surface, \nonumber \]
donde
\[P=\dfrac{n_{2}-n_{1}}{R}, \nonumber \]
se llama el poder de la superficie.
Para un espejo esférico con radio de curvatura R, vemos que
\[α_{1}=θ_{i} − ϕ, \nonumber \]
\[α_{2}=-θ_{r} − ϕ, \nonumber \]
donde tomamos en cuenta la convención de signos para los ángulos. Porque θ r = θ i encontramos
\[α_{2}=-α_{1}+2ϕ=-α_{1}+2\dfrac{y_{1}}{R}, \nonumber \]
donde usamos (\(\PageIndex{7}\)) con y A = y 1. Como se menciona en la Tabla\(\PageIndex{1}\), el índice de refracción después de la reflexión debe elegirse negativo. Esto significa que para los rayos que se propagan de derecha a izquierda, el índice de refracción en el vector de rayos debe elegirse negativo. Por lo tanto,
\[n_{2}α_{2}=-n_{1}α_{2}= n_{1}α_{1} -2n_{1}\dfrac{y_{1}}{R}. \nonumber \]
Entonces
\[\dbinom{n_{2}α_{2}}{y_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space reflector, \nonumber \]
donde
\[P=\dfrac{2n_{1}}{R} \nonumber \]
es el poder del espejo. Concluimos que la matriz de rayos para la reflexión por un espejo esférico es la misma que la de la refracción por una superficie esférica, siempre que n 2 sea reemplazada por −n 1. Cuando un rayo se propaga de derecha a izquierda, el índice de refracción de todos los medios e interfaces a través de los cuales se propaga el rayo, y en el que se refracta, debe tener un índice de refracción negativo. Después de que el rayo haya sido reflejado por segunda vez, debido a lo cual se propaga nuevamente de izquierda a derecha, todos los índices de refracción deberían volver a ser positivos. De esta manera, el método de matriz se puede aplicar a sistemas ópticos que consisten tanto en elementos refractantes, como lentes, como por elementos reflectantes.
Finalmente consideramos el caso de que entre los dos planos hay material homogéneo con índice de refracción n. En ese caso α 2 = α 1 e y 2 = y 1 + α 1 (z 2 − z 1), de ahí
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z_{2}-z_{1}}{n} & 1 \end{pmatrix},homogeneous\space space. \nonumber \]
Para dos planos entre los que hay una serie de componentes ópticos, posiblemente separados por regiones con material homogéneo (por ejemplo, aire), la matriz de rayos se puede obtener multiplicando las matrices de los componentes individuales y de las regiones homogéneas. El orden de multiplicación de las matrices es tal que la matriz más a la derecha corresponde al primer componente que se encuentra mientras se propaga, y así sucesivamente.
Cabe destacar que los rayos considerados en el enfoque de matriz de rayos permanecen en el mismo plano, es decir, el plano a través del rayo y el eje z. Estos rayos se llaman rayos meridionales. Al considerar solo los rayos meridionales, la imagen por sistemas ópticos se restringe a dos dimensiones. Los rayos no meridionales se llaman rayos sesgados. Los rayos sesgados no pasan por el eje óptico y no son considerados en la teoría paraxial.
2.5.3 La matriz de lentes
Aplicamos matrices de rayos a una lente. La figura\(\PageIndex{4}\) muestra una lente con dos superficies esféricas. El índice de refracción de la lente es n l y el del medio ambiente es n m y la distancia entre los vértices es d. Primero derivaremos la matriz que mapea el vector de rayos en el plano inmediatamente frente a la lente con el del plano inmediatamente detrás de la lente. Let
\[\dbinom{n_{m}α_{1}}{y_{1}}and\dbinom{n_{m}α_{2}}{y_{2}} \nonumber \]
ser dos vectores en los dos planos que corresponden al mismo rayo. El rayo es refractado primero por la superficie esférica con radio R1 y centro C1. Usando (\(\PageIndex{25}\)) y (\(\PageIndex{20}\)) se deduce que la matriz entre los vectores de rayos justo antes y justo detrás de la superficie esférica con radio R1 y centro C1 viene dada por
\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{l} - n_{m} }{R_{1}} \\ 0 & 1 \end{pmatrix} \nonumber \]
El rayo se propaga entonces sobre la distancia d a través del material del que está hecha la lente. La matriz que mapea vectores de rayos desde el plano dentro de la lente inmediatamente detrás de la superficie esférica izquierda a un vector de rayos en el plano inmediatamente anterior a la superficie esférica derecha sigue de (\(\PageIndex{27}\)):
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{d}{n_{l}} & 1 \end{pmatrix}. \nonumber \]
Finalmente, la matriz que mapea vectores de rayos desde el plano en la lente inmediatamente antes de la segunda superficie esférica a vectores en el plano inmediatamente detrás de ella es
\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{m} - n_{l} }{R_{2}} \\ 0 & 1 \end{pmatrix}. \nonumber \]
De ahí que la matriz que mapea vectores de rayos en el plano inmediatamente anterior a la lente a los vectores de rayos en el plano inmediatamente detrás de la lente viene dada por el producto de la matriz:
\[M=M_{3}M_{2}M_{1}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P_{1}-P_{2}+\dfrac{d}{n_{l}}P_{1}P_{2} \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},lens, \nonumber \]
donde
\[P_{1}=\dfrac{ n_{l} - n_{m} }{R_{1}},P_{2}=\dfrac{ n_{m} - n_{l} }{R_{2}}. \nonumber \]
La cantidad
\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2} \nonumber \]
se llama el poder de la lente. Tiene dimensión 1/longitud y se da en dioptrías (D), donde 1 D = m −1. El poder puede ser positivo y negativo. El eje z es el eje de simetría y se denomina eje óptico. El espacio a la izquierda de la lente se llama el espacio del objeto y ese a la derecha de la lente se llama el espacio de la imagen.
2.5.4 Enfoque con una lente delgada
Para una lente delgada los vértices V 1 y V 2 coinciden y d = 0, de ahí que (\(\PageIndex{34}\)) se convierte en
\[M=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix},thin\space lens, \nonumber \]
donde P = P 1 + P 2, con P 1 y P 2 dados por (\(\PageIndex{35}\)). El origen del sistema de coordenadas se elige en el vértice común V 1 = V 2. Para un rayo que emerge en el espacio de la imagen a la altura y 2 y paralelo al eje óptico: α 2 = 0, tenemos y 1 = y 2 y
\[n_{m} α _{1}=P_{y}. \nonumber \]
Si la potencia es positiva: P > 0, el ángulo α1 tiene el mismo signo que y 1, lo que implica que el rayo en el espacio del objeto ha intersectado el eje óptico en un punto F o con la coordenada z: z = f o satisfaciendo
\[\dfrac{1}{f_{o}}=\dfrac{α _{1}}{y _{1}} = \dfrac{n_{m}}{P}=\dfrac{n_{l}-n_{m}}{n_{m}}(\dfrac{1}{R_{1}}-\dfrac{1}{R_{2}}). \nonumber \]
El punto Fo se llama el primer punto focal o punto focal del objeto.
De igual manera, al considerar un rayo en medio 1 el cual es paralelo al eje óptico (α 1 = 0) y a la altura y 1, obtenemos n m α 2 = −P y 1 e y 2 = y 1. De ahí que cuando P > 0, el ángulo α 2 del rayo tiene signo opuesto a y 2 y por lo tanto el rayo en el espacio de la imagen se dobla de nuevo al eje óptico, dando como resultado un segundo punto focal o punto focal de imagen F i. Su coordenada z f i satisface:
\[\dfrac{1}{f_{i}}=-\dfrac{α _{2}}{y _{2}} = -\dfrac{n_{m}}{P}=-\dfrac{1}{f_{o}}. \nonumber \]
Cuando la potencia P de la lente es positiva, f i = −f o > 0, lo que significa que el primer y segundo puntos focales están en el espacio del objeto y de la imagen, respectivamente. Una lente con potencia positiva se llama convergente o positiva.
Una lente con potencia negativa se llama divergente y tiene f i = −f o < 0. Luego, los rayos incidentes paralelos al eje óptico se refractan lejos del eje óptico y parecen provenir de un punto frente a la lente con la coordenada z f i < 0. De ahí que el segundo punto focal no corresponda a una ubicación donde exista concentración real de intensidad lumínica y de ahí que sea virtual. El primer punto focal es un punto de objeto virtual, ya que sólo para un haz de rayos incidentes que están convergiendo a cierto punto detrás de la lente, la refracción negativa puede dar un haz de rayos que son todos paralelos al eje óptico.
Con los resultados obtenidos para las coordenadas focales podemos reescribir la matriz de lente de una lente delgada alternativamente como
\[M=\begin{pmatrix} 1 & -\dfrac{n_{m}}{f_{i}} \\ 0 & 1 \end{pmatrix},thin\space lens. \nonumber \]
2.5.5 Imágenes con una lente delgada
Primero consideramos la matriz general de rayos (\(\PageIndex{16}\)), (\(\PageIndex{17}\)) entre dos planos z = z 1 y z = z 2 y hacemos la siguiente pregunta: ¿cuáles son las propiedades de la matriz de rayos de manera que los dos planos son imágenes el uno del otro, o (como también se le llama a esto) son el conjugado del otro ? Claramente para que estos planos sean la imagen del otro, debemos tener que por cada coordenada de punto y 1 en el plano z = z 1, hay un punto con la coordenada y 2 en el plano z = z 2 tal que cualquier rayo a través (y 1, z 1) (dentro de algunos cono de rayos) pasará por punto (y 2, z 2). De ahí que para cualquier ángulo α 1 (en algún intervalo de ángulos) hay un ángulo α 2 tal que (\(\PageIndex{16}\)) es válido. Esto significa que para cualquier y 1 hay un y 2 tal que para todos los ángulos α 1:
\[y _{2}=Cn_{1}α _{1}+Dy _{1}, \nonumber \]
Esto requiere que
\[C = 0, condition\space for\space imaging. \nonumber \]
La relación de y 2 e y 1 da el aumento. De ahí
\[\dfrac{y _{2}}{y _{1}}=D, \nonumber \]
es el aumento de la imagen (esta cantidad tiene signo).
Para determinar la imagen de un punto mediante una lente delgada derivamos primero la matriz de rayos entre los planos z = z 1 < 0 y z = z 2 > 0 con una lente delgada en el medio con vértice en el origen. Esta matriz es el producto de la matriz para propagarse desde z = z 1 hasta el plano inmediatamente delante de la lente, la matriz de la lente delgada y la matriz para propagación desde el plano inmediatamente detrás de la lente hasta el plano z = z 2:
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z _{2}}{n _{m}} & 1 \end{pmatrix}\begin{pmatrix} 1 & -\dfrac{n _{m}}{f_{i}} \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -\dfrac{z _{1}}{n _{m}} & 1 \end{pmatrix}=\begin{pmatrix} 1+\dfrac{z _{1}}{f_{i}} & -\dfrac{n _{m}}{f_{i}} \\ -\dfrac{z _{1}}{n _{m}}+\dfrac{z _{2}}{n _{m}}+\dfrac{z _{1}z _{2}}{n _{m}f_{i}} & 1-\dfrac{z _{2}}{f _{i}} \end{pmatrix} \nonumber \]
La condición de imagen (\(\PageIndex{41}\)) implica:
\[-\dfrac{1}{s _{o}}+\dfrac{1}{s _{i}}=\dfrac{1}{f _{i}},Lensmaker's\space Formula. \nonumber \]
donde hemos escrito s o = z 1 y s i = z 2 para las coordenadas z del objeto y la imagen. Porque para la matriz de lente delgada (\(\PageIndex{43}\)): D = 1− z 2 /f i, se deduce usando (\(\PageIndex{44}\)) que la ampliación (\(\PageIndex{42}\)) viene dada por
\[M=\dfrac{y _{i}}{y _{o}}=1-\dfrac{s _{i}}{f _{i}}=\dfrac{s _{i}}{s _{o}}, \nonumber \]
donde hemos escrito ahora y o e y i en lugar de y 1 e y 2, respectivamente.
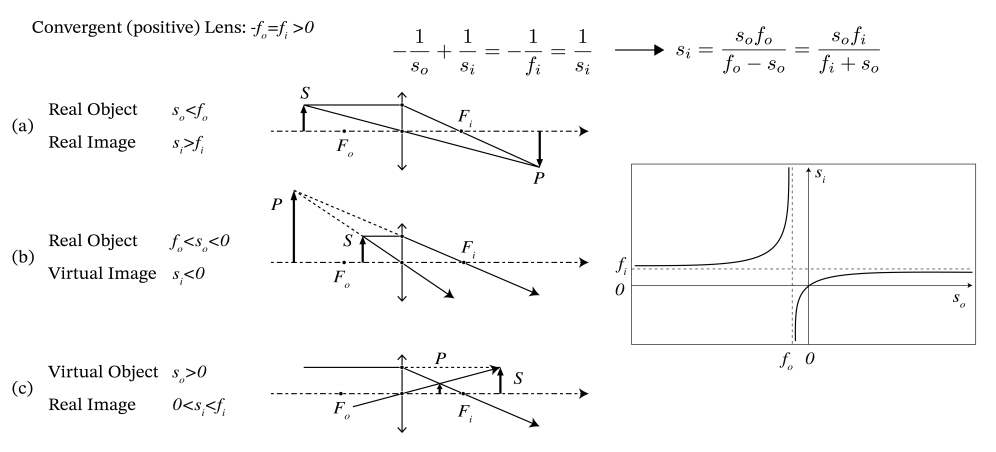
Para una lente positiva: f i > 0 y por lo tanto (\(\PageIndex{44}\)) implica que s i > 0 proporcionó |s o | < f i = |f o |, lo que significa que la imagen por una lente convergente es real si el objeto está más lejos de la lente que el primer punto focal F o. El caso s o > 0 corresponde a un objeto virtual, es decir, al caso de un haz convergente de rayos incidentes, que para un observador en el espacio del objeto parece converger a un punto a distancia tan detrás de la lente. Una lente convergente (f i > 0) hará entonces una imagen entre la lente y el segundo punto focal. Por el contrario, una lente divergente (f i < 0) puede convertir el haz convergente incidente en una imagen real solo si el punto del objeto virtual está entre la lente y el punto focal. Si el punto del objeto virtual tiene mayor distancia a la lente, la convergencia del haz incidente es demasiado débil y la lente divergente refracta entonces este haz en un haz divergente de rayos con vértice en el punto de imagen virtual frente a la lente (s i < 0).
También se puede construir la imagen con una regla. Considere la obtención de imágenes de un objeto finito S 1 S 2 como se muestra en la Figura\(\PageIndex{4}\). Sea y o la coordenada y de S 2. Tenemos y o > 0 cuando el objeto está por encima del eje óptico. Dibuja el rayo a través del punto focal F o en el espacio del objeto y el rayo a través del centro V de la lente. El primer rayo se vuelve paralelo en el espacio de la imagen. Este último cruza ambas superficies de la lente casi en sus vértices (casi coincidentes) y por lo tanto la refracción es opuesta en ambas superficies y el rayo sale de la lente paralelo a su dirección de incidencia. Además, se puede descuidar su desplazamiento lateral porque la lente es delgada. De ahí que el rayo que atraviesa el centro de la lente no se refracte. La intersección en el espacio de imagen de los dos rayos da la ubicación del punto de imagen P 2 de S2. La imagen es real si la intersección ocurre en el espacio de la imagen y es virtual de lo contrario. Para el caso de una lente convergente con un objeto real con y o > 0 como se muestra en la Figura\(\PageIndex{4}\), se deduce de los triángulos similares AVF i y P 2 P 1 F i que
\[\dfrac{y _{o}}{|y _{i}|}=\dfrac{f _{i}}{s _{i}-f _{i}}, \nonumber \]
donde usamos |f o | = f i. De los triángulos similares S 2 S 1 F o y BVF o:
\[\dfrac{|y _{i}|}{y _{o}}=\dfrac{f _{i}}{f _{o}-s _{o}}. \nonumber \]
(el valor absoluto de y i se toma porque según nuestra convención de signos y i en la Figura\(\PageIndex{4}\) es negativo mientras que (\(\PageIndex{44}\)) es una relación de longitudes). Al multiplicar estas dos ecuaciones obtenemos la forma newtoniana de la ecuación de lente:
\[x _{o}x _{i}=-f _{i}^2=-f _{o}^2, \nonumber \]
donde x o y x i son las coordenadas z del objeto y la imagen en relación con las del primer y segundo punto focal, respectivamente:
\[x _{o}=s _{o}-f _{o},x _{i}=s _{i}-f _{i}. \nonumber \]
De ahí que x o sea negativo si el objeto es t o la izquierda de Fo y x i es positivo si la imagen está a la derecha de F i.
El aumento transversal es
\[M=\dfrac{y _{i}}{y _{o}}=\dfrac{s _{i}}{s _{o}}= -\dfrac{x _{i}}{f _{i}} , \nonumber \]
donde la segunda identidad se deriva de considerar los triángulos similares ∆P 2 P 1 F i y ∆AVF i en la Figura\(\PageIndex{4}\). Una M positiva significa que la imagen es erecta, una M negativa significa que la imagen está invertida (como siempre es el caso de una sola lente).
Todas las ecuaciones también son válidas para lentes negativas delgadas y para objetos e imágenes virtuales. Algunos ejemplos de objetos reales y virtuales y puntos de imagen para una lente positiva y una negativa se muestran en las Figs. \(\PageIndex{5}\)y\(\PageIndex{6}\).
2.5.6 Dos lentes delgadas
Las imágenes por dos lentes delgadas L 1 y L 2 se pueden obtener fácilmente por construcción. Simplemente construimos la imagen obtenida por la primera lente como si la segunda lente no estuviera presente y usamos esta imagen como objeto (posiblemente virtual) para la segunda lente. En la Figura se muestra\(\PageIndex{7}\) un ejemplo donde la distancia entre las lentes es mayor que la suma de sus distancias focales. Primero se construye la imagen P' de S tal como se obtiene por L 1 como si L 2 no estuviera presente. Construimos la imagen intermedia P' debido a la lente L 1 usando los rayos 2 y 3. P 1 es una imagen real de la lente L 1 que también es objeto real para la lente L 2. El rayo 3 es paralelo al eje óptico entre las dos lentes y, por lo tanto, es refractado por la lente L2 a través de su punto focal posterior F 2i. El rayo 4 es el rayo desde P1 a través del centro de la lente L 2. El punto de imagen P es la intersección de los rayos 3 y 4.
En el caso de\(\PageIndex{8}\) la Figura la distancia d entre las dos lentes positivas es menor que sus distancias focales. La imagen intermedia P' es una imagen real para L 1 obtenida como la intersección de los rayos 2 y 3 que pasan por los puntos focales del objeto y la imagen F 1o y F 1i de la lente L 1. P' es ahora un punto de objeto virtual para la lente L 2. Para encontrar su imagen por L 2, dibuje el rayo 4 de P' a través del centro de la lente L 2 de nuevo a S (este rayo es refractado por la lente L 1 pero no por L 2) y dibuje el rayo 3 como refractado por la lente L 2. Dado que el rayo 3 es paralelo al eje óptico entre las lentes, pasa a través del punto focal posterior F 2i de la lente L 2. El punto de intersección de los rayos 3 y 4 es el punto final de imagen P.
Es fácil expresar la coordenada z s i con respecto al sistema de coordenadas con origen en el vértice de L 2 del punto final de la imagen, en el componente z s o con respecto al origen en el vértice de la lente L 1 del punto objeto. Utilizamos la fórmula del fabricante de lentes para cada lente mientras nos ocupamos de que se use el sistema de coordenadas locales adecuado en cada caso. La imagen intermedia P' debida a la lente L 1 tiene la coordenada z s 1i con respecto al sistema de coordenadas con origen en el vértice V1, que satisface:
\[\dfrac{1}{s_{o}}+\dfrac{1}{s_{1i}}=\dfrac{1}{f_{1i}}. \nonumber \]
P' es objeto para lente L 2 con coordenada z con respecto al sistema de coordenadas con origen en V 2 dado por: s 2o = s 1i − d, donde d es la distancia entre las lentes. De ahí que con s i = s 2i la Fórmula de Lensmaker para lente L 2 implica:
\[-\dfrac{1}{s_{1i}-d}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{2i}}. \nonumber \]
Al resolver (\(\PageIndex{51}\)) para s 1i y sustituir el resultado por (\(\PageIndex{52}\)), encontramos
\[s_{i}=\dfrac{-df_{1i} f_{2i}+ f_{2i}( f_{1i} -d)s_{o} }{ f_{1i}( f_{2i} -d) +( f_{1i}+ f_{2i} -d)s_{o} },two\space thin\space lenses. \nonumber \]
Al tomar el límite s o → −∞, obtenemos la coordenada z f i del punto focal de imagen de las dos lentes, mientras que s i → ∞ da la coordenada z f o del punto focal del objeto:
\[f_{i}=\dfrac{( f_{1i} -d) f_{2i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]
\[f_{o}=-\dfrac{( f_{2i} -d) f_{1i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]
Excepto cuando los índices de refracción del medio antes y después de la lente son diferentes, las distancias focales del objeto y de la imagen de una lente delgada son las mismas. Sin embargo, como se desprende de la fórmula derivada para un sistema óptico con dos lentes, las distancias focales del objeto y de la imagen son en general diferentes cuando hay varias lentes.
Por construcción usando la imagen intermedia, es claro que la ampliación del sistema de dos lentes es el producto de las ampliaciones de las dos lentes:
\[M=M_{1}M_{2}. \nonumber \]
Observaciones
1. Cuando f 1i + f 2i = d los puntos focales están en el infinito. Tal sistema se llama telecéntrico.
2. En el límite donde las lentes están muy juntas: d → 0, (\(\PageIndex{53}\)) se convierte en
\[-\dfrac{1}{s_{o}}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{1i}}+ \dfrac{1}{f_{2i}}. \nonumber \]
La distancia focal fi del sistema de dos lentes en contacto satisface así:
\[\dfrac{1}{f_{i}}=\dfrac{1}{f_{1i}}+\dfrac{1}{f_{2i}}. \nonumber \]
Dos lentes positivas en contacto cercano se hacen cumplir entre sí, es decir, la segunda lente positiva hace que la convergencia de la primera lente sea más fuerte. De igual manera, dos lentes negativas en contacto hacen un sistema más fuertemente negativo. Lo mismo se aplica para más de dos lentes en contacto cercano.
3. Aunque para dos lentes la coordenada de la imagen aún se puede expresar con relativa facilidad en la distancia del objeto, para sistemas con más lentes encontrar la matriz de rayos general y luego usar la condición de imagen (\(\PageIndex{41}\)) es una estrategia mucho mejor.
2.5.7 La lente gruesa
A la izquierda de la Figura se muestra\(\PageIndex{9}\) una lente gruesa. El primer punto focal se define como el punto cuyos rayos son refractados de tal manera que los rayos emergentes son paralelos al eje óptico. Al extender los rayos incidentes y emergentes por segmentos rectos, los puntos de intersección se encuentran en una superficie curva, que cerca del eje óptico, es decir, en la aproximación paraxial, se encuentra en buena aproximación un plano perpendicular al eje óptico. Este plano se denomina plano principal primario y su intersección con el eje óptico se denomina punto principal primario H1. Al considerar los rayos incidentes que son paralelos al eje óptico y por lo tanto enfocados en el punto focal posterior, el plano principal secundario y el punto principal secundario H2 se definen de manera similar (ver el dibujo a la derecha en la Figura\(\PageIndex{9}\)). Los planos principales no necesitan estar dentro de la lente. En particular para lentes de menisco, este no es el caso. Se puede observar en la Figura 2.18 que los planos principales son imágenes entre sí, con aumento unitario. De ahí que si un objeto se coloca en el plano principal primario (hipotéticamente si este plano está dentro de la lente), su imagen está en el plano principal secundario. La imagen es erecta y tiene aumento de unidad.
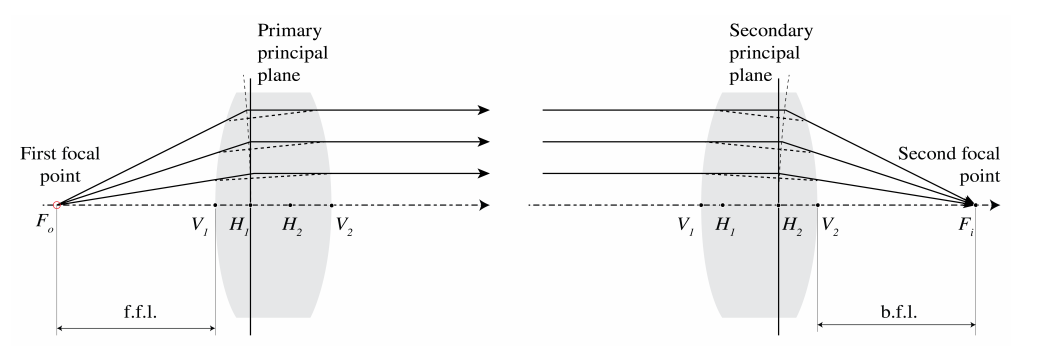
Recordamos el resultado (\(\PageIndex{32}\)) para la matriz de rayos entre los planos a través de los vértices delantero y trasero V 1, V 2 de una lente gruesa con índice de refracción n l y espesor d:
\[M_{V_{1}V_{2}}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},thick\space lens, \nonumber \]
donde
\[P_{1}=\dfrac{n_{l}-n_{m}}{R_{1}},P_{2}=\dfrac{n_{m}-n_{l}}{R_{2}}, \nonumber \]
y n m es el índice de refracción del medio ambiente, y
\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2}. \nonumber \]
Si h 1 es la coordenada z del primer punto principal H 1 con respecto al sistema de coordenadas con vértice de origen V 1, tenemos según (\(\PageIndex{27}\)) para la matriz de rayos entre el plano principal primario y el plano a través del vértice V 1
\[M_{1}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{1}}{n_{m}} & 1\end{pmatrix}. \nonumber \]
De igual manera, si h 2 es la coordenada del punto principal secundario H2 con respecto al sistema de coordenadas con V 2 como origen, la matriz de rayos entre el plano a través del vértice V2 y el plano principal secundario es
\[M_{2}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{2}}{n_{m}} & 1\end{pmatrix}. \nonumber \]
La matriz de rayos entre los dos planos principales es entonces
\[M_{H_{1}H_{2}}=M_{2}M_{V_{1}V_{2}}M_{1}. \nonumber \]
Las coordenadas h1 y h2 se pueden encontrar imponiendo a la matriz resultante la condición de imagen (\(\PageIndex{41}\)): C = 0 y la condición de que la ampliación debe ser la unidad: D = 1, que se desprende de (\(\PageIndex{42}\)). Omitimos los detalles y solo damos las expresiones resultantes aquí:
\[h_{1}=\dfrac{n_{m}}{n_{l}}\dfrac{P_{2}}{P}d, \nonumber \]
\[h_{2}=-\dfrac{n_{m}}{n_{l}}\dfrac{P_{1}}{P}d. \nonumber \]
Además, (\(\PageIndex{64}\)) se convierte en
\[M_{H_{1}H_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1\end{pmatrix}. \nonumber \]
Vemos que la matriz de rayos entre los planos principales es idéntica a la matriz de rayos de una lente delgada (\(\PageIndex{35}\)). Por lo tanto, concluimos que si se eligen las coordenadas en el espacio objeto con respecto al origen en el punto principal primario H 1, y las coordenadas en el espacio de imagen se eligen con respecto al origen en el punto principal secundario H2, las expresiones para el primero y segundo los puntos focales y para las coordenadas del punto de imagen en términos de la del punto objeto son idénticos a los de una lente delgada. Un ejemplo de imagen mediante una lente gruesa se muestra en la Figura\(\PageIndex{11}\).
2.5.8 Topes
Un elemento como el borde de una lente o un diafragma que determina el conjunto de rayos que pueden contribuir a la imagen, se denomina tope de apertura. Una cámara ordinaria tiene un diafragma variable.
La pupila de entrada es la imagen del tope de apertura por todos los elementos a la izquierda del tope de apertura. Si no hay lentes entre el objeto y el tope de apertura, el tope de apertura en sí es la pupila de entrada. De igual manera la pupila de salida es la imagen de la abertura parada por todos los elementos a la derecha de la misma. La pupila de entrada determina para un objeto dado el cono de rayos que ingresa al sistema óptico, mientras que el cono de rayos que sale y toma parte en la formación de la imagen está determinado por la pupila de salida (ver Figura\(\PageIndex{12}\)). Obsérvese que al construir la pupila de entrada como la imagen de la abertura se detiene por las lentes a la izquierda de la misma, se están propagando de derecha a izquierda. De ahí que el tope de apertura sea un objeto real en esta construcción, mientras que la pupila de entrada puede ser una imagen real o virtual. Los rayos utilizados en la construcción de la pupila de salida como la imagen de la abertura se detienen por las lentes que siguen al tope se propagan de izquierda a derecha. De ahí que también en este caso el tope de apertura sea un objeto real mientras que la pupila de salida puede ser una imagen real o virtual del tope de apertura.
Para cualquier punto objeto, el rayo principal es el rayo en el cono que pasa por el centro de la pupila de entrada, y por lo tanto también a través de los centros del tope de apertura y la pupila de salida. Un rayo marginal es el rayo que para un punto objeto en el eje óptico pasa a través del borde de la pupila de entrada (y por lo tanto también a través de los bordes del tope de apertura y la pupila de salida).
Para un diámetro fijo D de la pupila de salida y dado x o, la ampliación del sistema es de acuerdo con (\(\PageIndex{50}\)) y (\(\PageIndex{48}\)) dada por M = −x i /f i = f i /x o. De ello se deduce que cuando se incrementa fi, la ampliación aumenta. Un aumento mayor significa una menor densidad de energía, por lo tanto, un tiempo de exposición más largo, es decir, se reduce la velocidad de la lente. Las lentes de cámara generalmente se especifican con dos números: la distancia focal f i y el diámetro D de la pupila de salida. El número f es la relación entre la distancia focal y este diámetro:
\[f-number=\dfrac{f}{D}. \nonumber \]
Por ejemplo, f-número= 2 significa f = 2D. Dado que el tiempo de exposición es proporcional al cuadrado del número f, una lente con número f 1.4 es dos veces más rápida que una lente con número f 2.
