2.8: Aberraciones
- Page ID
- 129986
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
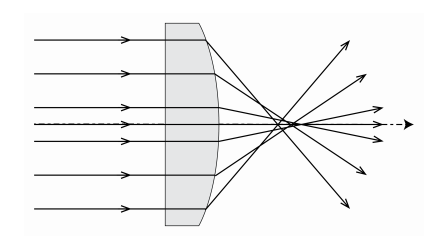
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Para diseñar sistemas ópticos avanzados la óptica geométrica gaussiana no es suficiente. En cambio, los rayos no paraxiales, y entre ellos también los rayos no meridionales, deben rastrearse utilizando un software basado en la Ley de Snell con el seno de los ángulos de incidencia y refracción. A menudo se trazan muchos miles de rayos para evaluar la calidad de una imagen. Se encuentra entonces que en general los rayos no paraxiales no se cruzan en el punto ideal de la imagen gaussiana. En lugar de un solo punto, se encuentra un diagrama de puntos que está más o menos confinado. La desviación de una imagen de punto ideal se cuantifica en términos de aberraciones. Se distingue entre aberraciones monocromáticas y cromáticas. Estos últimos son causados por el hecho de que el índice de refracción depende de la longitud de onda. Recordemos que en óptica geométrica paraxial la Ley de Snell (2.3.7) es reemplazada por: n i θ i = n t θ t, es decir sin θ i y sin θ t son reemplazadas por los términos lineales. Si en cambio se mantienen los dos primeros términos de la serie Taylor del seno, los errores en la imagen pueden cuantificarse mediante cinco aberraciones monocromáticas, las llamadas aberraciones primarias o Seidel. La más conocida es la aberración esférica, la cual es causada por el hecho de que para una lente esférica convergente, los rayos que hacen un ángulo grande con el eje óptico se enfocan más cerca de la lente que los rayos paraxiales (ver Figura\(\PageIndex{1}\)). La distorsión es una de las cinco aberraciones primarias. Provoca deformación de las imágenes debido a que el aumento depende de la distancia del punto del objeto al eje óptico.
Para obtener imágenes de alta calidad, las aberraciones tienen que reducirse añadiendo más lentes y optimizando las curvaturas de las superficies, los espesores de las lentes y las distancias entre ellas. Para sistemas de alta calidad, a veces se utiliza una lente con una superficie asférica. Los sistemas con aberraciones muy pequeñas son extremadamente caros, en particular si el campo de visión es grande, como es el caso de los sistemas de imagen litográfica utilizados en la fabricación de circuitos integrados.
2.7.1 Óptica de difracción
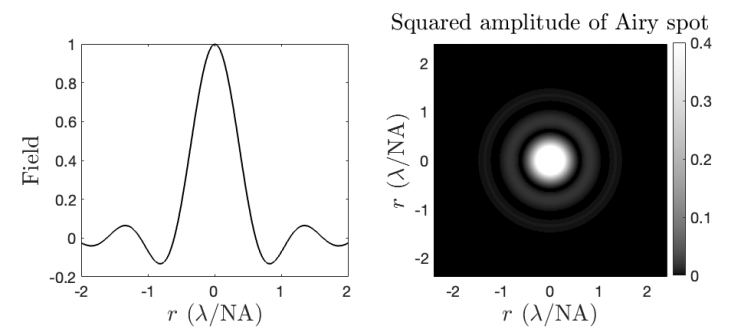
Las aberraciones se pueden cuantificar analizando el diagrama de puntos o, alternativamente, considerando la forma del frente de onda real en el espacio de la imagen, que en la óptica geemotrical gaussiana convergería al punto de imagen gaussiana. Las aberraciones hacen que el frente de onda se desvíe de una esfera perfecta. De acuerdo con un criterio generalmente aceptado formulado primero por Rayleigh, las aberraciones comienzan a deteriorar las imágenes considerablemente si las aberraciones del frente de onda causan diferencias de longitud de trayectoria de más de un cuarto de la longitud de onda. Cuando las aberraciones son menores que esto, el sistema se denomina difracción limitada. Un tratamiento muy completo de la teoría de la aberración se puede encontrar en el libro de Braat et al. Aunque la onda transmitida por la pupila de salida fuera perfectamente esférica, el frente de onda consiste únicamente en una sección circular de una esfera ya que el campo está limitado por la abertura. Una apertura provoca difracción, es decir, flexión y dispersión de la luz. Cuando se imagina un objeto puntual en el eje óptico, la difracción provoca la distribución de la luz llamada punto Airy, como se muestra en la Figura\(\PageIndex{3}\). El punto Airy tiene ancho completo a la mitad del máximo:
\[FWHM=0.6\dfrac{λ}{NA}, \nonumber \]
con NA= arcsin (a/si) es la apertura numérica (es decir, 0<NA<1) con un radio de la pupila de salida y si la distancia de la imagen predicha por la óptica geométrica gaussiana. La difracción depende de la longitud de onda y por lo tanto no puede ser descrita por la óptica geométrica, la cual se aplica en el límite de longitud de onda de fuga. Trataremos la difracción por aperturas en el Capítulo 6.