7.2: Resonador óptico

Ahora explicamos el funcionamiento de los láseres. Un láser consiste en

1. un resonador óptico;
2. un medio de amplificación.

En esta sección consideramos el resonador. Su función es obtener una alta densidad de energía lumínica y ganar control sobre las longitudes de onda de emisión.

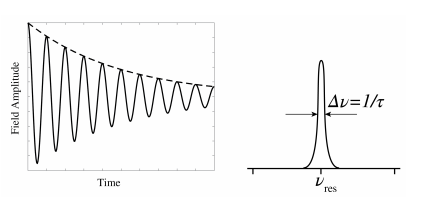
Un resonador, ya sea mecánico como un péndulo, un resorte o una cuerda, o eléctrico como un circuito LRC, tiene una o múltiples frecuencias de resonancia\(\nu_{\text {res.}}\). Cada resonador tiene pérdidas debido a que la oscilación se extingue gradualmente cuando no se suministra energía. Las pérdidas provocan una disminución exponencial de la amplitud de la oscilación, como se muestra en la Figura\(\PageIndex{1}\). Por lo tanto, la oscilación no es puramente monocromática sino que tiene un ancho de banda finito de orden\(\Delta \nu \approx 1 / \tau\) como se muestra en la Figura\(\PageIndex{1}\), donde\(\tau\) está el tiempo en el que la amplitud de la oscilación se ha reducido a la mitad del valor inicial.

Figura\(\PageIndex{1}\): Oscilación amortiguada (izquierda) y espectro de frecuencia de una oscilación amortiguada (derecha) con longitud de onda de resonancia y ancho de frecuencia igual al recíproco del tiempo de decaimiento.

El resonador óptico es una región llena de algún material con índice de refracción\(n\) limitado por dos espejos alineados altamente reflectantes a distancia\(L\). El resonador se llama cavidad Fabry-Perot. Deje que el\(z\) eje -se elija a lo largo del eje de la cavidad como se muestra en la Fig. \(\PageIndex{2}\), y supongamos que las direcciones transversales son tan grandes que la luz puede considerarse una onda plana que rebota hacia adelante y hacia atrás a lo largo del\(z\) eje -entre los dos espejos. Dejar\(\omega\) ser la frecuencia y\(k_{0}=\omega / c\) el número de onda en vacío. La onda plana que se propaga en la\(z\) dirección positiva viene dada por:\[E(z)=A e^{i k_{0} n z}. \nonumber \]

Para espejos muy buenos, la amplitud permanece sin cambios en las reflexiones, mientras que la fase normalmente cambia por\(\pi\). Por lo tanto, después de un viaje de ida y vuelta (es decir, dos reflexiones\(\PageIndex{1}\)) el campo () es (los posibles cambios de fase en los espejos se suman\(2 \pi\) y por lo tanto no tienen ningún efecto):\[E(z)=A e^{2 i k_{0} n L} e^{i k_{0} n z} . \nonumber \] Un campo alto se acumula cuando esta onda interfiere constructivamente con (\(\PageIndex{1}\)), es decir, cuando\[k_{0}=\frac{2 \pi m}{2 n L}, \quad \text { or } \quad \nu=\frac{k c}{2 \pi}=m \frac{c}{2 n L}, \nonumber \] para \(m=1,2, \ldots\). De ahí que, siempre que se pueda descuidar la dispersión del medio (\(n\)es independiente de la frecuencia), las frecuencias de resonancia están separadas por\[\Delta \nu_{f}=c /(2 n L), \nonumber \] lo que es el llamado rango espectral libre. Para un láser de gas que es\(1 \mathrm{~m}\) largo, el rango espectral libre es aproximadamente\(150 \mathrm{MHz}\).

Figura\(\PageIndex{2}\): Resonancias de Fabry-Perot.

Ejemplo\(\PageIndex{1}\)

Supongamos que la cavidad es\(100 \mathrm{~cm}\) larga y está llena de un material con índice de refracción\(n=1\). La luz con longitud de onda visible de\(\lambda=500 \mathrm{~nm}\) corresponde al número de modo\(m=2 L / \lambda=4 \times 10^{6}\) y el rango espectral libre es\(\Delta \nu_{f}=c /(2 L)=150 \mathrm{MHz}\).

Los múltiples reflejos de la luz láser dentro del resonador hacen que la longitud de la trayectoria óptica sea muy grande. Para un observador, las fuentes atómicas parecen estar a una distancia muy grande y la luz que sale de la cavidad se asemeja a una onda plana. Por lo tanto, la divergencia del haz no está limitada por el tamaño de la fuente, sino por la difracción debida a la apertura del espejo de salida.

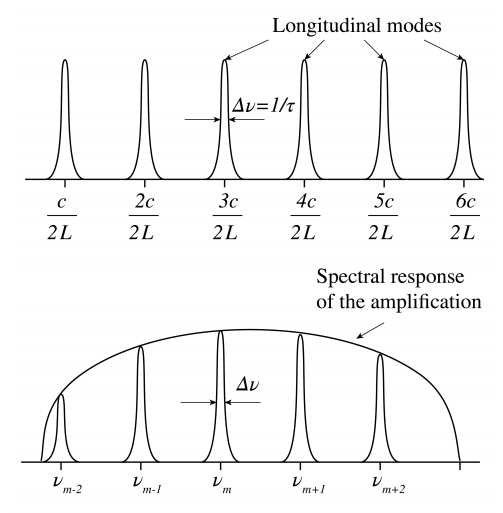
Debido a las pérdidas causadas por los espejos (que nunca reflejan perfectamente) y por la absorción y dispersión de la luz, las resonancias tienen un cierto ancho de frecuencia\(\Delta \nu\). Cuando se usa un resonador como láser, a uno de los espejos se le da una pequeña transmisión para acoplar la luz láser. Esto también contribuye a la pérdida del resonador. Para compensar todas las pérdidas, la cavidad debe contener un medio amplificador. Debido a la amplificación, los anchos de línea de resonancia dentro del ancho de banda del amplificador se reducen a líneas muy nítidas como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Frecuencias resonantes de una cavidad de longitud\(L\) cuando el índice de refracción\(n=1\). Con un amplificador dentro de la cavidad, se reducen los anchos de línea de las resonancias dentro del ancho de banda del amplificador. La envolvente es la función espectral de la amplificación.