2.11: Lentes Gruesas
- Page ID
- 127486
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La Figura II.16 muestra una lente gruesa de índice\(n_2\), un objeto O y una imagen I. Para una buena medida he puesto un medio de índice\(n_1\) a la izquierda de la lente y un medio de índice\(n_3\) a la derecha de la lente.

Si se le da la posición de O, ¿puede calcular la posición de la imagen?
Bueno, es fácil calcular la convergencia\(C_1\) cuando la luz llega a la primera superficie. Entonces podemos calcular fácilmente la convergencia\(C_2\) simplemente sumando la potencia de la primera interfaz. Y, si sabemos\(C_3\) (Sí, ahí está el roce) podemos calcular fácilmente\(C_4\). Vemos que la clave para resolver problemas de lentes gruesos es saber cómo cambia la convergencia con la distancia, por lo que haremos que sea nuestro próximo objetivo.

La Figura II.17 muestra un haz de luz, en un medio de índice\(n_2\), que converge al punto P, que se encuentra a una\(x\) distancia del plano A. La convergencia del haz a medida que sale del plano A es\(C_2 = n_2/x\). Cuando llega al plano B, que se encuentra a una distancia D del plano A, su convergencia es\( C_3 =n_2/(x-D)\). Cuando eliminamos\(x\), obtenemos
\[ C_3 = \frac{n_2C_2}{n_2 - DC_2} \label{eq:2.11.1} \]
por la fórmula que nos dice cómo cambia la convergencia con la distancia.
Volvamos ahora al problema de la Figura II.16.
Ejemplo\(\PageIndex{1}\)
Supongamos que los radios de curvatura de la primera y segunda caras son de 15 y 25 cm respectivamente, y la distancia entre las caras es de 50 cm. El índice de refracción del vidrio es\(n_2\) = 1.60. Supondremos que hay agua (\(n_1\)= 1.33) a la izquierda de la lente, y, a la derecha de la lente hay algún líquido con índice de refracción 1.42. El objeto está a 30 cm a la izquierda de la primera cara. ¿Dónde está la imagen?
Solución
El cálculo va de la siguiente manera (Ecuación\ ref {eq:2.11.1}):
\[ \begin{align*} C_1 &= -\dfrac{1.33}{30} = -0.044333 \, \text{cm}^{-1} \\[4pt] C_2 &= C_1 + \dfrac{1.60-1.33}{+15} = -0.026333 \, \text{cm}^{-1} \\[4pt] C_3 &= \dfrac{1.60\times C_2}{1.60 - 50 \times C_2} = -0.014446 \, \text{cm}^{-1} .\end{align*}\]
Observe que la luz está divergiendo en el momento en que llega a la segunda cara.
\[ C_4 = C_3 + \dfrac{1.42-1.60}{-25} = -0.007246 \, \text{cm}^{-1}. \nonumber\]
La luz sigue divergiendo, por lo que la imagen es virtual. La distancia de la imagen desde la segunda cara es de 1.42 ÷ 0.007 246 = 196 cm, y está a la izquierda de la segunda cara.
El aumento de una lente gruesa se encuentra fácilmente. El aumento producido por la primera cara es, como de costumbre\(C_1/C_2\), y luego hay un aumento adicional de\(C_3/C_4\) producido por la segunda cara. De esta manera el aumento general es\(\frac{C_1C_3}{C_2C_4}\), que es este caso es +3.356. La imagen se magnifica en tamaño y es erecta.
Este método para lentes gruesas también se puede utilizar para lentes y espejos separados. Aquí hay uno:
Ejemplo\(\PageIndex{2}\)
La Figura II.18 muestra una lente delgada separada de un espejo, y un objeto a 14 cm de la lente. ¿Dónde está la imagen?

Solución
\( C_1 = -1/14 = -0.071420 \)cm -1.
\( C_2 = C_1 +1/25 = -0.031429 \)cm -1.
\( C_3 = \frac{C_2}{1-40\times C_2}=-0.013924\)cm -1.
\( C_4 = C_3 + \frac{-2}{-30} =+0.053743\)cm -1.
La imagen es real. Es de 18.96 cm a la izquierda del espejo. El aumento es −0.60. La imagen está invertida y disminuida.
Por supuesto, quienes establecen exámenes pueden pensar en todo tipo de preguntas desagradables. Por ejemplo, podríamos tener una lente gruesa y un objeto, pero, en lugar de que se nos pida que busquemos la imagen, se nos puede decir la distancia de la imagen y se nos pida encontrar el índice de refracción, o el grosor, o uno de los radios. O, peor aún, tal vez no nos digan la distancia de la imagen, pero se nos podría decir su ampliación y si es real o virtual, o erecta o invertida, y se nos pide que busquemos otra cosa. ¡Hay infinitas posibilidades! Aquí hay uno.

La lente mostrada tiene radios de curvatura de 16 y 30 cm, y tiene un grosor de 5 cm. Un objeto está a 36 cm a la izquierda de la cara de 16 cm. Su imagen es de 50 cm a la derecha de la superficie de 30 cm. Demostrar que el índice de refracción es la solución positiva de
\(1845n^2 - 2417n - 520 = 0\).
Aquí hay otro.
Ejemplo\(\PageIndex{2}\)
La lente mostrada es de 4 cm de grosor y el índice de refracción es de 1.6. El radio de curvatura de la primera cara es de 15 cm. Un objeto está a 32 cm a la izquierda de la cara de 15 cm. Su imagen es real, invertida y magnificada por 22. Determinar el radio de curvatura de la segunda cara.

Solución
Pistas. La imagen es real. ¿Qué lado de la lente es? Se puede calcular fácilmente\(C_1 , C_2\) y\(C_3\), por lo que debe ser capaz\(C_4\) de obtener de la ampliación. La respuesta, por cierto, es de 80,1 cm — pero ¿es convexa a la derecha, como se muestra, o es cóncava a la derecha?
Uno más.
Ejemplo\(\PageIndex{4}\)
Las dos lentes están hechas de un sólido muy ligero cuyo índice de refracción es de sólo 1.3. (¡No estoy seguro de si hay tal cosa!) y se sumergen en un líquido de índice 1.4. Eso significa que la lente convexa es divergente. La segunda superficie de la segunda lente es un espejo reflectante. He indicado los radios de curvatura, y las lentes están separadas 40 cm. La luz paralela viene de la izquierda. ¿De dónde viene a un foco?
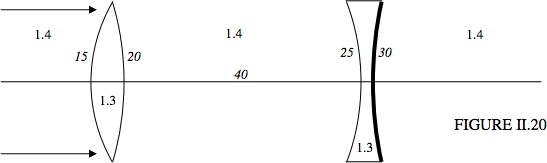
Solución
La convergencia inicial\(C_1 = 0\). Calcularé la convergencia después de que la luz llegue o salga de cada superficie o interfaz. Espero que la notación sea clara. Todas las convergencias están en cm −1.
\[\begin{align*} C_2 &= 0 + \dfrac{1.3-1.4}{+15} = -0.006. \\[4pt] C_3 &= -0.006 + \dfrac{1.4-1.3}{-20} = -0.0116. \\[4pt] C_4 &= \dfrac{1.4C_3}{1.4-40C_3} = -0.00875.\\[4pt] C_5 &= -0.00875 + \dfrac{1.3-1.4}{-25} = -0.00475.\\[4pt] C_6 &= -0.00475 + \dfrac{-2\times 1.3}{30} =-0.091416. \\[4pt] C_7 &= -0.091416 + \dfrac{1.4-1.3}{+25} = -0.087416.\\[4pt] C_8&=\dfrac{1.4C_7}{1.4-40C_7} = -0.02499319265.\\[4pt] C_9 &= C_8 + \dfrac{1.3-1.4}{-20} = -0.02999319265.\\[4pt] C_{10} &= C_9 + \dfrac{1.4-1.3}{-15} = -0.03665985931. \end{align*}\]
Por último\(C_{10} = \frac{1.4}{x}\),, entonces\(x = -38.188 908 15 \left(=-\frac{22035}{577}\right)\) cm.
Es decir, el foco es de 38.2 cm a la derecha de la lente convexa, o 1.8 cm a la izquierda de la lente cóncava.
Ejercicio\(\PageIndex{1}\)
Redactar un problema en el que se le da al alumno la distancia focal de dos lentes, y las posiciones de objeto e imagen, y se le pide al alumno que calcule la distancia entre las lentes.


