2.12: Planos Principales
- Page ID
- 127450
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Considera una lente gruesa o un sistema de dos lentes separadas. En la Figura II.21,\(F_1\) es el primer punto focal y\(H_1\) es el primer plano principal. En Digure II.22,\(F_2\) es el segundo punto focal y\(H_2\) es el segundo plano principal
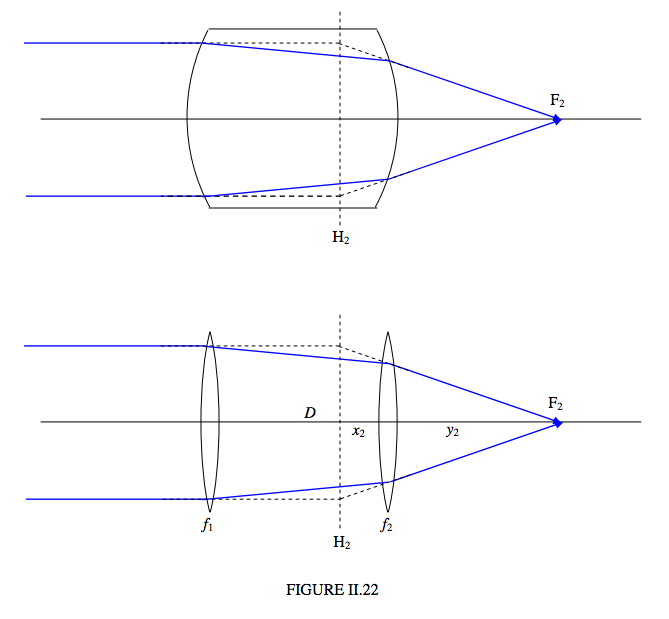
Me refiero ahora a la segunda parte de la fFigura II.22, y supongo que las distancias focales de las dos lentes son\(f_1\) y\(f_2\), y la distancia entre ellas es\(D\). Ahora invito al lector a calcular las distancias\(x_2\) y\(y_2\). La distancia se\(x_2\) puede calcular considerando algunos triángulos similares (que el lector deberá agregar al dibujo), y la distancia se\(y_2\) puede calcular calculando las convergencias de la\(C_1, C_2,C_3,C_4\) manera que ya es familiar. Deberías obtener
\[ x_2 = \frac{Df_2}{f_1+f_2-D}. \label{eq:2.12.1} \]
y
\[ y_2=\frac{f_2(f_1-D)}{f_1+f_2-D}. \label{eq:2.12.2} \]
Invito además al lector a imaginar que las dos lentes van a ser reemplazadas por una sola lente situada en el plano\(H_2\) para llevar la luz al\(F_2\) mismo foco que obtuvieron las dos lentes originales. La pregunta es: ¿cuál debe ser la distancia focal f de esta lente única? La respuesta es obviamente\(x_2 + y_2\), que viene a
\[ f = \frac{f_1f_2}{f_1+f_2-D}. \label{eq:2.12.3} \]
El ocular de un instrumento óptico como un telescopio o un microscopio es generalmente una combinación de dos (o más) lentes, llamadas lente de campo y lente ocular. Generalmente están dispuestos de manera que la distancia entre los dos sea igual a la mitad de la suma de las distancias focales de las dos lentes. Ahora veremos que esta disposición, con dos lentes hechas del mismo vidrio, está relativamente libre de aberración cromática.
Recordemos que el poder de una lente en el aire viene dado por
\[ P = \frac{1}{f}=(n-1)\left(\frac{1}{r_1}+\frac{1}{r_2}\right) \label{eq:2.12.4} \]
Aquí\(r_1\) y\(r_2\) están los radios de curvatura de las dos superficies, y\(n\) es el índice de refracción del vidrio. Para abreviar, voy a escribir Ecuación\(\ref{eq:2.12.4}\) como
\[ P = \frac{1}{f} = \mu S, \label{eq:2.12.5} \]
dónde\(\mu = n-1\) y\(S= \left(\frac{1}{r_1}+\frac{1}{r_2}\right) \). Siendo así, la ecuación se\(\ref{eq:2.12.3}\) puede escribir
\[ P = \mu(S_1+S_2)- \mu ^2SD_1S_2 \label{eq:2.12.6} \]
Esta ecuación muestra cómo la posición del foco\(F_2\) varía con el color. En particular,
\[ \frac{dP}{d\mu} = S_1 + S_2 - 2 \mu DS_1S_2, \label{eq:2.12.7} \]
lo que demuestra que la posición de\(F_2\) no varía con el color siempre que la distancia entre las lentes sea
\[ D= \frac{S_1+S_2}{2\mu S_1S_2}. \label{eq:2.12.8} \]
Al volver a Ecuación\(\ref{eq:2.12.5}\), vemos que esto se traduce en
\[ \underline{\underline{D= \frac{1}{2}(f_1+f_2).}} \label{eq:2.12.9} \]