2.14: Ejercicio
- Page ID
- 127487
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ejercicio\(\PageIndex{1}\)
Un objeto se coloca a 90 cm a la izquierda de una lente delgada en el aire. La imagen es real y está a 99 cm a la derecha de la lente.
Sin embargo, si el medio a la derecha de la lente es agua (índice de refracción 1.33), la imagen es virtual y está a 76 cm a la izquierda de la lente.
Y si el medio a la izquierda de la lente es agua (y a la derecha está el aire) la imagen es real y 47 cm a la derecha de la lente.
Calcular los dos radios de curvatura y el índice de refracción del vidrio.
Ejercicio\(\PageIndex{2}\)
Un objeto se coloca 100 cm a la izquierda de la primera superficie (A) de una lente gruesa (espesor = 10 cm) en el aire. La imagen es real y está a 25 cm a la derecha de la segunda superficie (B).
Sin embargo, si el medio a la derecha de la segunda superficie (B) es agua (índice de refracción 1.33), la imagen es real y 41 cm a la derecha de la superficie B.
Y si el medio a la izquierda de la superficie A es agua (y a la derecha de B es aire) la imagen es real y 92 cm a la derecha de la lente.
Calcular los dos radios de curvatura y el índice de refracción del vidrio.
Ninguno de estos dos problemas es probable que aparezca en una situación práctica, ¡pero son muy buenas prácticas para problemas difíciles de lentes! Soluciones en la página siguiente — ¡pero sin echar un vistazo hasta que las hayas probado!
Soluciones
1. Primero:
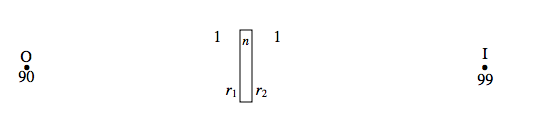
\[\frac{1}{99} = -{1}{90} +\frac{n-1}{r_1}+\frac{1-n}{r_2}.\label{eq:2.14.1} \]
Segundo:

\[-\frac{-1.33}{76}=-\frac{1}{90}+\frac{n-1}{r_1}+\frac{1.33-n}{r_2}. \label{eq:2.14.2} \]
(Puede que tengas la tentación de pensar que el lado izquierdo de esta ecuación debería ser\(\frac{1}{76}\). Asegúrate de entender por qué esto está mal).
Tercero:

\[\frac{1}{47} = -\frac{1.33}{90}+\frac{n-1.33}{r_1}+\frac{1-n}{r_2}.\label{eq:2.14.3} \]
La física ya está terminada. Todo lo que hay que hacer es resolver las tres ecuaciones para las tres incógnitas. Yo empezaría por dejar\( x=r_1, y=r_2, z = n\). Las ecuaciones se convierten entonces en:
\[z(x-y)-x+y=0.021212121,\label{eq:2.14.4} \]
\[z(x − y) − x + 1.33 y = − 0.006388889 \label{eq:2.14.5} \]
y
\[z(x − y) − 1.33 x + y = 0.036054374.\label{eq:2.14.6} \]
Estos son fáciles de resolver:
\(x= − 0.044977, \quad y = − 0.083639, \quad z = + 1.54864.\)
Así
\(r_1 = 22.23 \text{cm},\qquad r_2 = 11.96 \text{cm},\qquad n=1.5549 \text{cm} \)
La lente es una lente de menisco positivo (es decir, más gruesa en el medio), siendo ambas superficies convexas a la derecha. Se ve así:
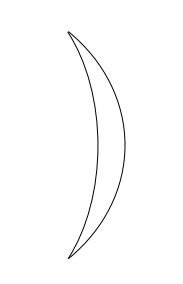
2.
Primero:

\[C_1 = -\frac{1}{100}\label{eq:2.14.7} \]
\[C_2 = -\frac{1}{100} + \frac{n-1}{r_1} = \frac{100n-100-r_1}{100r_1}\label{eq:2.14.8} \]
\[C_3 = \frac{nC_2}{n-10C_2} = \frac{100n^2 - 100n-r_1n}{100r_1n+10r_1 - 1000n + 1000}\label{eq:2.14.9} \]
\[ C_4 = \frac{100n^2-100n - r_1n}{100r_1n+10r_1-1000n+1000}+\frac{1-n}{r_2}=\frac{1}{25}\label{eq:2.14.10} \]
Segundo:

\[C_1 = -\frac{1}{100}\label{eq:2.14.11} \]
\[C_2 = -\frac{1}{100}+\frac{n-1}{r_1} = \frac{100n-100-r_1}{100r_1}\label{eq:2.14.12} \]
\[C_3 = \frac{nC_2}{n-10C_2}=\frac{100n^2-100n-r_1n}{100r_1n+10r_1-1000n+1000}\label{eq:2.14.13} \]
\[C_4= \frac{100n^2-100n-r_1n}{100r_1n+10r_1-1000n+1000}+\frac{1.33-n}{r_2} =\frac{1.33}{41}\label{eq:2.14.14} \]
Hasta el momento, hemos obtenido dos ecuaciones de aspecto complicado (\(\ref{eq:2.14.10}\)y\(\ref{eq:2.14.14\)) en las tres incógnitas\(r_1, r_2\) y\(n\), y estamos a punto de embarcarnos en obtener una tercera ecuación del tercer experimento, después de lo cual tendremos que enfrentar la desagradable tarea de resolver las tres ecuaciones. ¡Pero mira! — antes de seguir adelante, podemos descubrir que ya podemos resolver para\(r_2\) a partir de Ecuaciones\(\ref{eq:2.14.10}\) y\(\ref{eq:2.14.14}\). Yo lo hago
\[r_2 = - 43.645 161 29 \text{cm}\label{eq:2.14.15} \]
de manera que la segunda superficie es cóncava hacia la izquierda, es decir, se abomba hacia la derecha. ¡Esto fue una inesperada pieza de buena fortuna! Ahora podemos pasar al tercer experimento.
Tercero:

\[C_1 = -\frac{1.33}{100}\label{eq:2.14.16} \]
\[C_2 = -\frac{1.33}{100 }+\frac{n-1.33}{r_1}=\frac{100n-133-1.33r_1}{100r_1}\label{eq:2.14.17} \]
\[C_3 = \frac{nC_2}{n-10C_2}=\frac{100n^2-133n-1.33r_1n}{100r_1n+13.3r_1-1000n+1330}\label{eq:2.14.18} \]
\[C_4= \frac{100n^2-133n-1.33r_1n}{100r_1n+13.3r_1 -1000n + 1300}+\frac{1-n}{r_2} = \frac{1}{92}\label{eq:2.14.19} \]
Ahora podemos resolver Ecuaciones\(\ref{eq:2.14.10}\) y\(\ref{eq:2.14.19}\), o\(\ref{eq:2.14.14}\) y\(\ref{eq:2.14.19}\) para\(r_1\) y\(n\). El muy concienzudo querrá resolverlos usando\(\ref{eq:2.14.10}\)\(\ref{eq:2.14.19}\) y luego repetir la solución usando\(\ref{eq:2.14.14}\) y\(\ref{eq:2.14.19}\), y verificar que den la misma respuesta, y luego verificará además que las soluciones correctas se han obtenido por sustitución en cada una de las tres ecuaciones en giro. Siendo un poco menos concienzudo, voy a usar Ecuaciones\(\ref{eq:2.14.10}\) y\(\ref{eq:2.14.19}\), y luego verificaré que las soluciones obtenidas satisfacen Ecuación\(\ref{eq:2.14.14}\).
Me resulta más fácil resolver ecuaciones en\(x\) y en\(y\) lugar de en\(r_1\) y\(n\), así voy a dejar\(x = r_1\) y\(y = n\). Entonces, teniendo en cuenta que ya hemos encontrado que\( r_2 = -43.645 161 29\), Ecuaciones\(\ref{eq:2.14.10}\) y\(\ref{eq:2.14.19}\) convertirse, respectivamente, después de un poco de álgebra y aritmética,
\[\frac{100y^2 -100y -xy}{100xy+10x-1000y+1000} = by +c \label{eq:2.14.20} \]
y
\[\frac{100y^2-100ay-axy}{100xy+10ax-1000y+1000a}=by+d,\label{eq:2.14.21} \]
donde
a = +1.33
b = -0.02291204730
c = +0.06291204630
d =+0.03379161252
Después de álgebra y aritmética un poco más tediosas pero rutinarias, estas se convierten
\[Axy^2 +By^2 + C_1xy + D_1x+E_1y+ F_1 = 0\label{eq:2.14.22} \]
y
\[Axy^2 + By^2+C_2xy+D_2x+E^2y+F_2 = 0, \label{eq:2.14.23} \]
donde
A = 2.291204730
B = 77.08795270
C 1 = -7.062084 257
D 1 = -0.6291204730
E 1 = -14.17590540
F 1 = -62.91204730
C 2 = -4,403431023
D 2 = -0.449295447
E 2 = -68.74536457
F 2 = -44.92954465.
¡Entonces tenemos que resolver estas dos ecuaciones! Estos pueden resolverse, por ejemplo, por el método descrito en la Sección 1.9 del Capítulo 1 de las notas sobre Mecánica Celestial. Como ya tengo un programa de computadora que hace eso, lo usé y obtuve\(x = 15.386908\) y\(y = .1 518865\). Así, la solución para la lente es
\( r_1 = + 15.39 \text{cm} \qquad r_2 = -43.65 \text{cm} \qquad n = 1.519\)
La primera superficie es convexa a la izquierda, y la segunda superficie es convexa a la derecha. Es decir, el cristalino es “gordo”, abultado en el medio.
Como comprobación de que nuestra aritmética está bien, podemos verificar que esta solución también satisface Ecuación\( \ref{eq:2.14.14}\). (¡Lo hace!)
Como una comprobación adicional, el lector podría ahora querer comenzar con estos números, y una distancia de objeto de 100 cm, y ver si da como resultado las tres distancias de imagen dadas en el problema original. (¡Lo hace!)
Otra forma de resolver ecuaciones\( \ref{eq:2.14.22}\) y\( \ref{eq:2.14.23}\) es restar la primera de la segunda para obtener
\[axy+bx+cy +d =0, \label{eq:2.14.24} \]
cuando
\(a\)= 2.658653234
\(b\)= 0.179825026
\(c\)= -54.56945917
\(d\)= 17.98260265.
Luego puede expresar\(x\) y una función de\(y\) y sustituir en Ecuación\( \ref{eq:2.14.22}\) (o en\( \ref{eq:2.14.23}\), o ambos como un cheque). Luego tiene una sola ecuación cúbica en\(y\), en lugar de dos ecuaciones simultáneas en\(x\) y\(y\), de la siguiente manera:
\[(Ba-Ac_y^3+(E_1a+Bb-C_1c-Ad)y^2+(F_1a+E_1b-D_1c-C_1d)y+F_1b-D_1c =0.\label{eq:2.14.25} \]
Numéricamente, esto es
\[329.9799377y^3- 450.4024164y^2 - 77.14660950y - 6.294\times10^{-5} =0. \label{eq:2.14.26} \]
La única raíz real positiva de esto es\(y (= n) = 1.518864\), que es la misma que obtuvimos antes. El valor de\(x (= r_1)\) se encuentra entonces fácilmente, a partir de la Ecuación\(\ref{eq:2.14.24}\), que es 15.3869 cm, como antes.
Ejercicio\(\PageIndex{3}\)
Una lente convergente tiene una distancia focal de 40 cm en el aire. ¿Cuál es su distancia focal cuando se sumerge en agua, de índice de refracción 1.333?
Después de un momento pensarlo exigirás que te digan el índice de refracción del vaso. Después de pensarlo más, concluirás que no solo necesitas conocer el índice de refracción del vidrio, sino que también necesitas conocer la forma (radios de curvatura de las superficies) de la lente.
Entonces, aquí está la pregunta correctamente establecida.
Una lente biconvexa está hecha de vidrio de índice de refracción 1.5. Los radios de curvatura de sus superficies son de 25 cm y 100 cm. ¿Cuál es su distancia focal en el aire? ¿Cuál sería su distancia focal si se sumergiera en agua de índice de refracción 4/3? ¿Cuál sería su distancia focal si se sumergiera en bisulfuro de carbono de índice de refracción 5/3?
Ejercicio\(\PageIndex{4}\)
Una lente tiene una distancia focal en el aire de 30 cm.
Un bloque de vidrio con el mismo índice de refracción que la lente anterior tiene una burbuja de aire dentro de él exactamente del mismo tamaño y forma de la lente anterior. ¿Cuál es la distancia focal de esta burbuja en forma de lente?
Quizás te estés preguntando si necesitas conocer la forma de la lente, o el índice de refracción del cristal. Te dejaré reflexionar.
Ejercicio\(\PageIndex{5}\)
Un doblete cementado delgado está hecho de dos lentes delgadas cementadas juntas, como se muestra en el dibujo a continuación. Los radios de curvatura en cm se indican en el dibujo. El índice de refracción de la lente de la izquierda es\(n_1\), y el de la lente de la derecha es\(n_2\). La combinación da como resultado una lente doblete divergente global de distancia focal de 127 cm.

Como resultado de un error de fabricación, los dos tipos de vidrio se intercambian inadvertidamente, y se realiza una lente doblete como se muestra a continuación:

Esta combinación da como resultado una lente doblete convergente global de lente focal de 72 cm. Calcular los índices de refracción de los dos tipos de vidrio.
Aquí están mis soluciones a los problemas 3 a 5
Soluciones
3. La distancia focal en el aire viene dada por
\(\frac{}{} = 0 +\frac{1.5-1.0}{25} + \frac{1.0-1.5}{-100}, \qquad \text{whence} \underline{\underline{f = 40 \text{cm}}} \)
La distancia focal en el agua viene dada por
\( \frac{\frac{4}{3}}{f} = 0 + \frac{\frac{3}{2}-\frac{4}{3}}{25} + \frac{\frac{4}{3}-\frac{3}{2}}{-100}, \qquad \text{whence} \underline{\underline{f = 160 \text{cm}}}\)
La distancia focal en CS 2 viene dada por
\(\frac{\frac{5}{3}}{f} = 0 + \frac{\frac{3}{2}-\frac{5}{3}}{25}+\frac{\frac{5}{3}-\frac{3}{2}}{-100}, \qquad \text{whence} \underline{\underline{f = -200 \text{cm}}} \)
4. Independientemente de la forma de la lente, la distancia focal de la lente de vidrio en el aire viene dada por
\( \frac{1}{f_{\text{lens}}}= (n-1) \left(\frac{1}{r_1}-\frac{1}{r_2}\right),\)
mientras que la distancia focal de la burbuja en vidrio viene dada por
\(\frac{1}{f_{\text{bubble}}}= (n-1) \left(\frac{1}{r_1}-\frac{1}{r_2}\right).\)
Así
\(\underline{\underline{f_\text{bubble} = -n \times f_\text{lens} = -30n \quad \text{cm}}}\)
5. Las distancias focales de los dos dobletes están relacionadas con los índices de refracción por
\( -\frac{1}{127}= \frac{n_1-1}{40} +\frac{n_2-n_2}{-22}+\frac{1-n_2}{50}\)
y
\(\frac{1}{72} = \frac{n_2-1}{40}+\frac{n_1-n_2}{-22}+\frac{1-n_1}{50}\)
Estas ecuaciones pueden ser reescritas
\( 1968n_1-18288n_2 + 803 = 0 \)
y
\(1296n_1 -1395n_2 + 374 = 0,\)
con soluciones
\(\underline{\underline{ n_1 = 1.521 \qquad n_2= 1.682}}\)


