3.2: La lupa

Dos puntos sobre una lupa para empezar. En primer lugar, aparentemente bastante pocas personas entienden cómo usar este complicado instrumento científico. La forma correcta de usarlo es sujetarlo lo más cerca posible de tu ojo. El segundo punto es que no magnifica en absoluto. El tamaño angular de la imagen es exactamente el mismo que el tamaño angular del objeto.

Antes de examinar la lupa, probablemente sea útil comprender solo un poco sobre el funcionamiento del ojo humano. No soy bióloga, soy muy comprensiva sobre cualquier discusión de ojos, así que voy a mantener esto lo más básico posible. Cuando la luz ingresa a la superficie frontal o córnea del ojo, se refracta para llegar a enfocarse en la superficie posterior de la retina. La imagen en la retina es una imagen real, invertida, pero el cerebro de alguna manera corrige para eso, para que los objetos se vean bien hacia arriba. Si bien la mayor parte de la refracción se realiza en la córnea, es posible algún ajuste en la distancia focal efectiva gracias a una lente flexible, cuya potencia se puede ajustar por medio de los músculos ciliares. El ajuste de esta lente nos permite acomodar o llevar a un foco objetos que se encuentran a diferentes distancias de nosotros.

Para un ojo en buen estado en una persona joven, el ojo y los músculos ciliares están más relajados cuando el ojo está puesto para llevar a un foco luz de un objeto infinitamente distante —es decir, cuando el ojo está puesto para recibir y llevar a un foco luz que es paralela antes de que entre en el ojo. Para poder enfocarse en un objeto cercano, los músculos ciliares tienen que hacer un poco de esfuerzo para aumentar la potencia de la lente. Pueden aumentar la potencia de la lente solo hasta el momento, sin embargo, y la mayoría de la gente no puede enfocarse en un objeto que esté más cerca que una cierta distancia conocida como el punto cercano. Para los jóvenes el punto cercano suele tomarse para ser de 10 pulgadas o 25 cm en los cálculos. El punto real real puede diferir de persona a persona; la cifra de 25 cm es un punto cercano “estándar”. Con las personas mayores, el punto cercano retrocede, de manera que 25 cm está demasiado cerca para mayor comodidad, y la lente se vuelve menos flexible.

Cuando utilizamos correctamente una lupa (sujetándola muy cerca del ojo) la colocamos automáticamente de manera que el objeto que estamos mirando esté en el punto focal de la lente, y en consecuencia la luz paralela emerge de la lente antes de que entre en nuestro ojo. No pensamos en esto. Es solo que los músculos ciliares del ojo están más relajados cuando están listos para llevar luz paralela a un foco. Es simplemente lo más cómodo de hacer. La figura III.2 muestra una lupa en el trabajo. Como es habitual, los ángulos son pequeños y la lente es delgada.

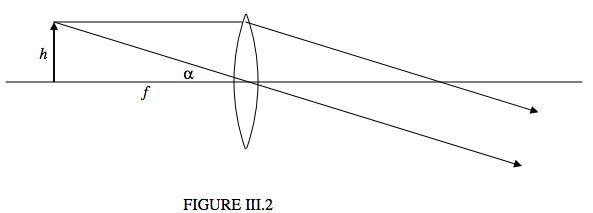
El objeto se encuentra en el plano focal de la lente. Dibujo dos rayos desde la punta del objeto. Uno es paralelo al eje, y, después de pasar por la lente, pasa a través del foco en el otro lado de la lente. El otro pasa por el centro de la lente. (Dado que la lente es delgada, este rayo no se desplaza lateralmente). Rayos paralelos emergen de la lente. El ojo está inmediatamente a la derecha del cristalino, y lleva fácilmente los rayos paralelos a un foco en la retina.

Aunque la lente en realidad no produce una imagen, a veces se dice que la lente produce “una imagen virtual al infinito”. El tamaño angular de esta imagen virtual es\(\alpha\), que es también el tamaño angular del objeto, es decir\(\alpha = h/f\). Así, el tamaño angular de la imagen es el mismo que el tamaño angular del objeto, ¡y la lente no se ha magnificado en absoluto!

Sin embargo, si colocas el objeto a una distancia\(f\) (tal vez a unos pocos cm) del ojo sin usar la lente, simplemente no podrías enfocar tu ojo en él. Sin la lente, lo más cercano que puedas poner el objeto a tu ojo sería\(D\), la distancia al punto cercano - 25 cm para un ojo joven. El tamaño angular del objeto sería entonces solamente\(h/D\).

Por lo tanto, el aumento angular de una lupa se define como

\[\dfrac{\text{angular size of the image (which is}\space h/f )}{\text{angular size of the object when the object is at the near point (which is}\space h/D )}\]

De ahí que la ampliación sea igual a\(D/f\). Se toma que el punto cercano sea de 25 cm, de manera que una lente de distancia focal de 2.5 cm tenga un aumento angular de 10.

Si traes el objeto un poco dentro del plano focal, la luz que emerge del otro lado divergirá, por así decirlo a partir de una imagen virtual que ya no está en el infinito. (Figura III.3).

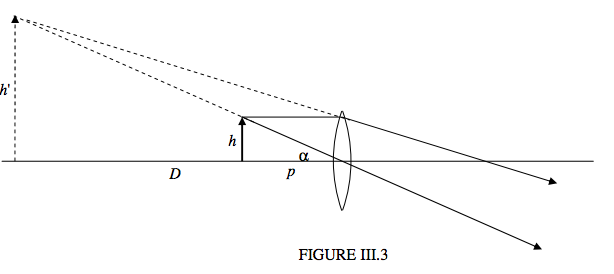
No tiene sentido, sin embargo, acercar la imagen que el punto cercano. Si lo llevas al punto cercano, ¿cuál debe ser la distancia del objeto p? Un simple cálculo de lente lo demuestra\(p = \frac{fD}{f+D}\). Por lo tanto, el tamaño angular de la imagen es\(\frac{h(f + D)}{fD}\). Dado que el tamaño angular del objeto cuando el objeto está en el punto cercano es\(h/D\), el aumento angular es ahora\(\frac{D}{f}\) + 1 cuando la imagen está en el punto cercano. Esto, para nuestra lente\(f\) = 2.5 cm, el aumento angular es entonces de 11.