3.5: El Telescopio

Nuestro propósito aquí no es describir en profundidad los detalles del diseño moderno del telescopio, sino simplemente dar los principios básicos de un telescopio simple a un nivel necesario para responder preguntas de examen de primer año y no necesariamente para describir un telescopio por el que uno podría realmente ser capaz de ver cualquier cosa a través. Un estudiante avanzado de astronomía que quiera detalles de telescopios reales tendrá que buscar en otra parte. Dicho esto, los principios básicos de un telescopio simple siguen aplicándose a los telescopios reales. La Figura III.6, entonces, ilustra un telescopio en su forma más simple. Debido a la dificultad de dibujar diagramas con ángulos pequeños, el telescopio se ve muy rechoncho comparado con uno real. Para hacer un dibujo más realista, la mayoría de los ángulos deben ser menores de aproximadamente un grado.

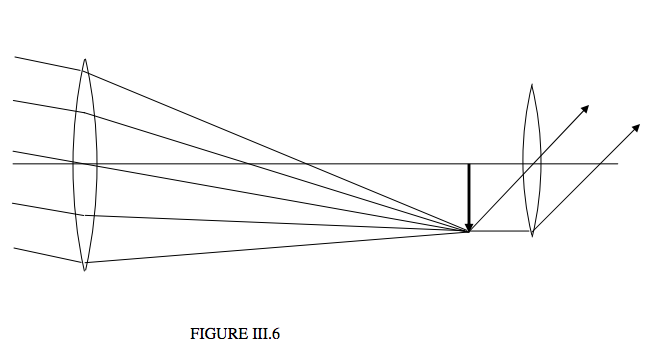
Vemos en el lado izquierdo de la figura un haz paralelo de luz proveniente de un objeto distante fuera del eje. La primera lente con la que se encuentra es el vidrio objeto. Su función es producir una imagen real en su plano focal, y la distancia entre el vidrio objeto y esta imagen primaria es\(f_1\), la distancia focal del vidrio objeto. En un verdadero telescopio de observación de aves, el vidrio objeto en realidad es un doblete acromático corona-pedernal que lleva a todos los colores casi al mismo enfoque. En un gran telescopio astronómico, en lugar de una lente, la imagen primaria está formada por un gran espejo cóncavo que a menudo es de forma paraboloidal en lugar de esférica.

Si el telescopio es un telescopio astronómico destinado a la fotografía, eso es todo lo que le queda. No hay segunda lente. La imagen primaria cae directamente sobre una placa fotográfica o película o CCD. Supongamos que estamos mirando a la Luna, cuyo radio angular es de aproximadamente un cuarto de grado y cuyo radio lineal real es de unos 1740 km. La distancia de la Luna es de unos 384,000 km. Supondremos que el telescopio apunta recto al centro de la Luna, y que el haz de luz que viene desde la izquierda de la figura III.6 viene del miembro superior de la Luna. La imagen del miembro superior de la Luna es la punta de la flecha gruesa. El radio de la imagen de la Luna (es decir, la longitud de la flecha gruesa) es\(f_1 \tan \frac{1}{4}^\alpha\). Supondremos que estamos utilizando un telescopio bastante grande, con una distancia focal de diez metros. El radio de la imagen primaria es entonces de 4.4 cm, mientras que el radio del objeto (la Luna) es de 1740 km. Así, la función del vidrio objeto es producir una imagen que es muy, muy, mucho más pequeña que el objeto. El aumento lineal es 4.4/174.000.000 o\(2.5 \times 10^{−8}\). Esto también es igual a la distancia de imagen dividida por la distancia del objeto, que es 10/384,000,000. ¡Y pensaste que un telescopio magnifica!

Sin embargo, en lugar de usar el telescopio para la fotografía, queremos “mirar a través” del telescopio. No queremos una placa fotográfica en la posición de la imagen real. En cambio, lo único que tenemos que hacer es mirar la imagen real con una lupa, y eso es lo que es la segunda lente de la Figura III.6. Esta segunda lente, que es solo una lupa (¡que, ya hemos visto en la Sección 3.3, tampoco magnifica!) se llama ocular. Como es habitual con una lupa, lo que estamos viendo (que es la imagen primaria producida por el cristal objeto, pero que sirve de objeto para el ocular) se coloca en el plano focal del ocular, de manera que la luz paralela emerge del ocular. Como se explica en la Sección 3.3 no tienes que pensar en esto — tus músculos ciliares están más relajados cuando el ojo está listo para recibir luz paralela. El ocular de un telescopio generalmente se puede mover hacia adentro y hacia afuera hasta que la imagen aparezca nítida para su ojo relajado. Así, la imagen primaria está en el plano focal del vidrio objeto y también del ocular, y la distancia entre el vidrio objeto y el ocular es\(f_1 + f_2\), donde\(f_1\) y\(f_2\) son las distancias focales del vidrio objeto y el ocular respectivamente. He dibujado los dos rayos habituales de la imagen primaria (que es el objeto para el ocular), a saber, uno que va recto por el centro de la lente, y otro paralelo al eje, que posteriormente pasa por el punto focal del ocular.

La Figura III.7 es la Figura III.6 redibujada con todos los rayos menos dos eliminados, a saber, el rayo que pasa por el centro del vidrio objeto y el rayo que pasa por el centro del ocular.

Aunque, como hemos visto, el tamaño lineal de la imagen primaria es mucho más pequeño que (¡es decir, centímetros en lugar de miles de kilómetros!) el objeto, lo que cuenta cuando estamos mirando a través de un telescopio es la ampliación angular, que es la relación entre el tamaño angular de la imagen y el tamaño angular del objeto, es decir, la relación\(\beta/\alpha\). Y como, como de costumbre, estamos tratando con ángulos pequeños (el diámetro angular de la Luna es de solo aproximadamente medio grado) —aunque es difícil dibujar un diagrama realista con ángulos tan pequeños— esta relación es igual a\(f_1/f_2\). Tenga en cuenta que la definición del aumento angular es la relación entre el tamaño angular de la imagen y el tamaño angular del objeto (¡y esta vez no agregamos “cuando el objeto está en el punto cercano”!) , mientras que\(f_1/f_2\) es cómo podemos calcularlo. Así, si te preguntan qué se entiende por el aumento angular de un telescopio, y dices “\(f_1/f_2\)” no obtendrás nada de diez —y merecidamente.

En cualquier caso, para una gran ampliación, se necesita un cristal objeto de distancia focal larga y un ocular de distancia focal corta. Generalmente tienes la opción de varios oculares para elegir.

Cabe señalar que la ampliación no es el atributo más importante de un gran telescopio astronómico. Los telescopios astronómicos grandes tienen grandes espejos primarios principalmente para recoger la mayor cantidad de luz posible.

Ejercicio\(\PageIndex{1}\)

Se utiliza un telescopio con un ocular que se magnifica 8 veces. El aumento angular del telescopio cuando se utiliza con este ocular es de 200. ¿Cuál es la distancia entre el vidrio objeto y el ocular?

Responder

628.125 cm.

Una cosa es extraña del “telescopio” descrito hasta ahora: ¡la imagen está al revés! De hecho para fines astronómicos esto no importa en absoluto, y no hay nada “malo”. Para un telescopio diseñado para uso terrestre, sin embargo, como para la observación de aves, queremos que la imagen sea el camino correcto hacia arriba. En telescopios más antiguos esto se hizo con dos lentes adicionales; en los telescopios modernos la imagen se invierte con prismas adicionales.

El lector astuto puede notar que hay algo más mal con las Figuras III.6 y 7. El objeto produce una imagen primaria real, y luego examinamos esa imagen primaria real con una lupa. Pero mira el rayo que va desde la punta de la imagen primaria a través del centro del ocular. ¿De dónde vino? ¡No parece haber pasado nunca por el cristal objeto! Parte de la respuesta a esto es que los ángulos en los dibujos son groseramente exagerados (es demasiado difícil dibujar diagramas con ángulos realistas pequeños), y que si los ángulos fueran dibujados correctamente, efectivamente se vería que este rayo pícaro había pasado a través del vidrio objeto. Pero esto es solo una parte de la respuesta, y un telescopio con solo las dos lentes mostradas tendría un campo de visión muy pequeño.

En la práctica un ocular consta de dos lentes separados por una corta distancia. Estas dos lentes se llaman lente de campo y lente ocular. En una disposición, la lente de campo coincide con la imagen primaria, es decir, la imagen primaria formada por el vidrio objeto cae exactamente sobre la lente de campo. La lente de campo no afecta en absoluto la ampliación; simplemente sirve para doblar parte de la luz del vidrio objeto hacia el cristalino del ojo. El rayo pícaro al que hemos llamado la atención ha sido doblado hacia el cristalino del ojo por el lente de campo. Esta disposición funcionaría, aunque un problema que surgiría es que los trozos de polvo en la superficie de la lente de campo estarían en enfoque nítido cuando se vean con la lente ocular. Por lo tanto, la lente de campo a menudo está dispuesta para no coincidir exactamente con la imagen primaria. También se puede mostrar (Sección 2.12) que si la separación de las lentes de campo y ojo es igual a la mitad de la suma de sus distancias focales, el ocular está libre de aberración cromática. El diseño del ocular podría ocupar fácilmente un capítulo completo, y no es raro que un buen ocular tenga seis o más componentes; solo mencionamos este problema en particular para ilustrar algunos de los puntos a considerar en el diseño óptico.

Volvamos a nuestro sencillo telescopio de sólo dos lentes. Veamos las cosas desde el punto de vista del ocular (que, en nuestro simple telescopio, consiste solo en el cristalino del ojo). Si ahora consideramos el vidrio objeto como un objeto, podemos entender que el ocular producirá una imagen real de este “objeto”. Véase la Figura III.8.

La imagen real del vidrio objeto producido por el ocular se llama pupila de salida del telescopio, y el vidrio objeto es la pupila de entrada del telescopio. Toda la luz que pasa por la pupila de entrada también pasa por la pupila de salida. Puedes ver fácilmente la pupila de salida a unos milímetros del ocular si sostienes un par de binoculares frente a ti a la distancia del brazo. La notación como “10% 50”, que se ve en un par de binoculares significa que el aumento angular es de 10 y el diámetro del vidrio objeto es de 50 mm. Si miras las pupilas de salida de un par de binoculares que estás considerando comprar, asegúrate de que sean circulares y no cuadrados. Si son cuadrados, parte de la luz que pasó por la pupila de entrada está siendo obstruida, probablemente por prismas inadecuados dentro de los binoculares, y no estás obteniendo tu valor completo de 50 milímetros. El tamaño de la pupila de salida debe ser aproximadamente igual al tamaño de la pupila de entrada de su ojo. Esto es de aproximadamente 4 mm en la luz del sol y unos 7 mm por la noche, por lo que debes considerar si vas a usar los binoculares principalmente para la observación de aves o principalmente para observar las estrellas.

Justo dónde está el alumno de salida, y ¿qué tan grande es? “¿Dónde?” es una pregunta tan importante como “¿qué tan grande?” — la distancia entre el ocular y la pupila de salida es el alivio ocular. Quieres que esta distancia sea pequeña si no usas gafas. Si eres meramente miope o hipermetrópico, no hay necesidad de que uses tus gafas al usar binoculares o un telescopio; simplemente puedes ajustar el enfoque del telescopio. Si usas anteojos para corregir el astigmatismo, sin embargo, seguirás necesitando tus anteojos cuando uses los binoculares o telescopio, por lo que necesitarás un alivio ocular más grande.

Para encontrar el alivio ocular, o la distancia de la pupila de salida del cristalino del ojo, recuerde que la distancia entre el vidrio objeto y el ocular es\(f_1 + f_2\), y la distancia focal del ocular es\(f_2\). Por lo tanto, el alivio ocular viene dado por

\[\dfrac{1}{q}= -\dfrac{1}{f_1+f_2}+\frac{1}{f_2}\]

o

\[q = \dfrac{f_2(f_1+f_2)}{f_1}.\]

La relación entre el tamaño de la pupila de entrada y el tamaño de la pupila de salida es igual a la relación de sus distancias desde el ocular. Esto es justo\(f_1/f_2\), que es el aumento angular del telescopio. Así, el diámetro de la pupila de salida de un par de\(10 \times 50\) prismáticos es de 5 mm — simplemente divida el diámetro del vidrio objeto por el aumento.