4.2: Aberración esférica

Comenzaremos por observar la aberración esférica resultante de la reflexión de un espejo esférico. Hasta ahora hemos asumido que un haz de luz paralelo, después de la reflexión de un espejo esférico, llega a un foco en un punto, y que la distancia del punto focal a la superficie del espejo es la mitad del radio de curvatura del espejo, como en la Figura IV.1:

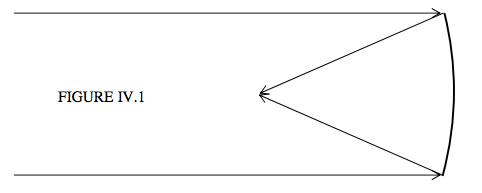
Esto es aproximadamente cierto para un espejo de apertura pequeña (“apertura” significa la relación entre el diámetro y la distancia focal). Este no es el caso, sin embargo, para un espejo de gran apertura. En la Figura IV.2 he dibujado un espejo hemisférico. Supongo que hay un haz de luz incidente (no dibujado) entrando horizontalmente desde la izquierda, y he dibujado los rayos después de la reflexión del espejo. (Algunos de los rayos se reflejarán por segunda vez desde la superficie antes de finalmente escapar, pero no he dibujado los rayos después de una segunda reflexión porque solo desordenarían el diagrama y no son pertinentes para describir lo que quiero describir. Se puede observar que los rayos reflejados están delimitados por una envolvente conocida como curva cáustica, mostrada como una curva roja discontinua en la Figura IV.2.

¿Podemos encontrar la ecuación a esta curva cáustica?

Tomaremos el centro de curvatura del espejo como origen O de coordenadas, y supondremos que el radio de curvatura del espejo es\(a\). Consideremos las aventuras de un rayo de luz que viene en paralelo al\((x)\) eje horizontal y a una altura\(h\) de éste. La ecuación al rayo de luz entrante es justa\(y = h\), y la ecuación a la superficie del espejo es\( x^2+y^2=a^2\). Un poco de geometría de coordenadas nos permitirá determinar que la ecuación al rayo reflejado es

\[y = \frac{h}{a^2-2h^2}\left[\left(2 \sqrt{a^2-h^2}x-a^2\right)\right], \label{eq:4.2.1} \]

y que cruza el\(x\) -eje en un punto C tal que

\[OC = \frac{a^2}{2\sqrt{a^2-h^2}}. \label{eq:4.2.2} \]

También es conveniente escribir estas fórmulas en términos del ángulo\(\theta\), que viene dado por\(h = a\sin \theta\). Después de un poco de álgebra y aplicación de algunas identidades trigonométricas, obtenemos

\[ y = x \tan 2 \theta - \frac{a\sin\theta}{\cos2\theta}\label{eq:4.2.3} \]

para la ecuación al rayo reflejado, y

\[ OC = \frac{1}{2} a \sec \theta. \label{eq:4.2.4} \]

Podemos escribir Ecuación\(\ref{eq:4.2.3}\) como

\[ f(x,y;\theta)= x\tan2\theta-\frac{a\sin\theta}{\cos2\theta}-y=0.\label{eq:4.2.5} \]

De nuestras notas matemáticas olvidadas, amarillentas y mohosas, recordamos que para encontrar la ecuación a la envolvente de una familia de curvas de la forma\(f(x,y;\theta)=0\), tenemos que eliminar el parámetro\(\theta\) de esa ecuación y la ecuación\(\frac{\partial f}{\partial \theta}=0\). Después de un poco más de álgebra y más aplicación de identidades trigonométricas, encontramos que esta última ecuación llega a

\[ x=a\cos\theta.(\frac{3}{2}-\cos^2\theta).\label{eq:4.2.6} \]

Entonces, todo lo que tenemos que hacer es eliminar el parámetro\(\theta\) de Ecuaciones\(\ref{eq:4.2.3}\) y\(\ref{eq:4.2.6}\), y esto nos daría la\(x , y\) ecuación a la curva cáustica. Estas dos ecuaciones son, de hecho, las ecuaciones paramétricas a la curva cáustica. Ahora no sé lo fácil que sería eliminar\(\theta\). Dado que la ecuación\(\ref{eq:4.2.6}\) es una ecuación cúbica en\(\cos \theta\), sospecho que podría no ser particularmente fácil. Pero (como suele ser el caso de dos ecuaciones paramétricas a una curva) podemos trazar felizmente la curva numéricamente, sin tener que eliminar el parámetro algebraicamente. Así, para trazar la curva roja en la Figura IV.2, I varió\(\theta\) de −90° a +90°, y se calculó a\(x\) partir de la Ecuación\(\ref{eq:4.2.6}\), y luego calculé\(y\) a partir de la Ecuación\(\ref{eq:4.2.3}\).

Para evitar aberraciones esféricas, los espejos telescópicos se pueden hacer en forma paraboloidal. Se puede demostrar que un haz de luz incidente, que viene en paralelo al eje de un espejo paraboloidal, después de la reflexión llegará a un único punto focal, es decir, en el foco de la parábola. Prueba de ello se da en la Sección 2.4 del Capítulo 2 de mis notas de Mecánica Celestial y no se repite ahí. En ese Capítulo, también se muestra que, si se gira un cubo de líquido alrededor de un eje vertical, la superficie del líquido tomará una forma paraboloidal, y ahí se hace mención de dos aplicaciones a la fabricación de espejos paraboloidales. En una, se gira una cuba de vidrio fundido, y se enfría gradualmente hasta que el vidrio se solidifica en una forma paraboloidal. En el otro, se gira un contenedor de mercurio, la superficie del mercurio toma una forma paraboloidal, y este paraboloide líquido se usa luego como espejo principal de un telescopio reflectante. Si bien solo se puede observar cerca del cenit, se han obtenido algunos excelentes resultados. No voy a repetirlo aquí, pero quizá quiera referirse a las notas antes mencionadas, ya que aquí es pertinente.

Esta propiedad (de que la luz se refleja desde la superficie de una parábola a un solo punto focal) se aplica solo a la luz que viene en paralelo al eje del paraboloide. En consecuencia, los espejos de telescopios paraboloidales solo tienen un campo de visión bastante estrecho. Un telescopio Schmidt utiliza un espejo esférico (de ahí un gran campo de visión) y, para evitar aberraciones esféricas, se monta una placa correctora frente al espejo. Por lo general, el espejo esférico está en el “extremo inferior” del tubo telescopio, y la placa correctora está en el “extremo superior”. La placa correctora provoca que la luz que viene en paralelo al tubo del telescopio, pero a cierta distancia del eje del tubo, diverja ligeramente del eje antes de alcanzar el espejo esférico. De esta manera toda la luz entrante, después de la reflexión del espejo, llega a un foco en un solo punto.

Una lente también sufre de aberración esférica, por supuesto, pero no se presta a análisis tan simples como para un espejo esférico. Se necesita realizar un trazado numérico detallado de rayos para encontrar la forma exacta de la curva cáustica para una lente. Mostramos, sin embargo, en la Sección 1.4 del Capítulo 1, que la refracción incluso en una superficie plana produce aberración esférica.

Uno podría preguntarse, dado que un espejo paraboloidal cuando se usa en el eje está libre de aberración esférica, si una lente hecha con superficies paraboloidales, también está libre de aberración esférica. Ay, eso no es así.

Sin embargo, se puede diseñar una lente con superficies esféricas que minimicen la aberración esférica, mediante la elección adecuada de los radios o curvatura de las superficies de la lente. A esto se le llama “doblar la lente”.

Por ejemplo, la Figura IV.4 muestra cinco lentes, en las que he escrito, al lado de cada superficie, su radio de curvatura en cm. En lo que sigue asumo que la lente es “delgada” en el sentido de que su grosor es muy pequeño en comparación con cualquier otra distancia que se esté discutiendo. Si el índice de refracción es 1.6, cada una de estas lentes tiene una distancia focal de 20 cm.

Se puede caracterizar la forma de una lente por medio de su factor de forma.

\[ q=\frac{r_1+r_2}{r_1-r_2}\label{eq:4.2.7} \]

En la Figura IV.4 he escrito el factor de forma encima de cada lente.

Para la luz que entra horizontalmente cerca del eje, la distancia focal de cada una de estas lentes es de 20 cm. Sin embargo, la luz que entra horizontalmente a cierta distancia del eje, después de pasar a través de la lente, cae un poco por debajo de 20 cm. Podemos caracterizar la aberración esférica por la cantidad que se queda corta. Suponiendo que las lentes son delgadas (en comparación con cualquier otra distancia en consideración) calculé el déficit para un rayo de luz que viene de la izquierda a una altura de 1 cm del eje. Esto se muestra en la Figura IV.5, en la que he dibujado el déficit (etiquetado como “Aberración” en la figura) versus factor de forma\(q\). Se ve que la aberración es menor para un factor de forma de aproximadamente\(q = −0.38\). Los radios de las curvaturas de la lente deben satisfacer la ecuación así\(\ref{eq:4.2.7}\) como\(q = −0.38\)

\[\frac{1}{f}=(n-1)\left(\frac{1}{r_1}-\frac{1}{r_2}\right), \label{eq:4.2.8} \]

de manera que, para\(f\) = 20 cm y\(q\) = −0.38, los radios de curvatura para la menor aberración esférica deben ser\(r_1\) = 17.4 cm y\(r_2\) = −38.7 cm.

Por supuesto, ¡tienes que usar la lente de la manera correcta! Si le das la vuelta, o si la luz viene por la derecha, el factor de forma es +0.38, y la aberración esférica no es mínima. Eso sí, el mínimo es bastante superficial, por lo que puedes variar el factor de forma una cantidad justa sin aumentar groseramente la aberración esférica.