26.5: El universo en expansión
- Page ID
- 127884
Objetivos de aprendizaje
Al final de esta sección, podrás:
- Describir el descubrimiento de que las galaxias se separan más a medida que evoluciona el universo
- Explicar cómo usar la ley del Hubble para determinar distancias a galaxias remotas
- Describir modelos para la naturaleza de un universo en expansión
- Explicar la variación en la constante del Hubble
Llegamos ahora a uno de los descubrimientos más importantes jamás realizados en astronomía: el hecho de que el universo se está expandiendo. Antes de describir cómo se realizó el descubrimiento, debemos señalar que los primeros pasos en el estudio de las galaxias llegaron en un momento en que las técnicas de espectroscopia también estaban dando grandes avances. Los astrónomos que utilizaban grandes telescopios podían registrar el espectro de una tenue estrella o galaxia en placas fotográficas, guiando sus telescopios para que permanecieran apuntando al mismo objeto durante muchas horas y recogieran más luz. Los espectros resultantes de galaxias contenían una gran cantidad de información sobre la composición de la galaxia y las velocidades de estos grandes sistemas estelares.
Observaciones pioneras de Slipher
Curiosamente, el descubrimiento de la expansión del universo comenzó con la búsqueda de marcianos y otros sistemas solares. En 1894, el controvertido (y rico) astrónomo Percival Lowell estableció un observatorio en Flagstaff, Arizona, para estudiar los planetas y buscar vida en el universo. Lowell pensó que las nebulosas espirales podrían ser sistemas solares en proceso de formación. Por lo tanto, pidió a uno de los jóvenes astrónomos del observatorio, Vesto M. Slipher (Figura\(\PageIndex{1}\)), fotografiara los espectros de algunas de las nebulosas espirales para ver si sus líneas espectrales podrían mostrar composiciones químicas como las esperadas para planetas recién formados.
El principal instrumento del Observatorio Lowell era un telescopio refractario de 24 pulgadas, que no se adaptaba en absoluto a las observaciones de nebulosas espirales débiles. Con la tecnología disponible en esos días, las placas fotográficas tuvieron que ser expuestas durante 20 a 40 horas para producir un buen espectro (en el que las posiciones de las líneas pudieran revelar el movimiento de una galaxia). Esto a menudo significaba seguir exponiendo la misma fotografía a lo largo de varias noches. A partir de 1912, y realizando esfuerzos heroicos a lo largo de un periodo de unos 20 años, Slipher logró fotografiar los espectros de más de 40 de las nebulosas espirales (que resultarían todas ser galaxias).
Para su sorpresa, las líneas espectrales de la mayoría de las galaxias mostraron un sorprendente desplazamiento al rojo. Por “desplazamiento al rojo” queremos decir que las líneas en los espectros se desplazan hacia longitudes de onda más largas (hacia el extremo rojo del espectro visible). Recordemos del capítulo sobre Radiación y Espectros que se ve un corrimiento al rojo cuando la fuente de las ondas se aleja de nosotros. Las observaciones de Slipher mostraron que la mayoría de las espirales están corriendo a grandes velocidades; la velocidad más alta que midió fue de 1800 kilómetros por segundo.
Solo unas pocas espirales, como las Galaxias Andrómeda y Triangulum y M81, todas las cuales ahora se sabe que son nuestras vecinas cercanas, resultaron acercarse a nosotros. Todas las demás galaxias se estaban alejando. Slipher anunció por primera vez este descubrimiento en 1914, años antes de que Hubble demostrara que estos objetos eran otras galaxias y antes de que nadie supiera lo lejos que estaban. Nadie en ese momento sabía del todo qué hacer con este descubrimiento.
Ley del Hubble
Las profundas implicaciones de la obra de Slipher se hicieron evidentes solo durante la década de 1920. Georges Lemaître era sacerdote belga y astrónomo entrenado. En 1927, publicó un artículo en francés en una oscura revista belga en la que sugería que vivimos en un universo en expansión. El título del artículo (traducido al inglés) es “Un universo homogéneo de masa constante y radio creciente que da cuenta de la velocidad radial de las nebulosas extragalácticas”. Lemaître había descubierto que las ecuaciones de relatividad de Einstein eran consistentes con un universo en expansión (como lo había hecho el científico ruso Alexander Friedmann independientemente en 1922). Lemaître luego pasó a utilizar los datos de Slipher para apoyar la hipótesis de que el universo en realidad se está expandiendo y para estimar la tasa de expansión. Inicialmente, los científicos prestaron poca atención a este artículo, quizás porque la revista belga no estaba ampliamente disponible.
Mientras tanto, Hubble estaba haciendo observaciones de galaxias con el telescopio de 2.5 metros en el monte. Wilson, que entonces era el más grande del mundo. Hubble realizó las observaciones clave en colaboración con un hombre notable, Milton Humason, quien abandonó la escuela en octavo grado y comenzó su carrera astronómica conduciendo un tren mula por el sendero en el monte Wilson hasta el observatorio (Figura\(\PageIndex{2}\)). En esos primeros días, los suministros tenían que ser traídos de esa manera; incluso los astrónomos subieron a la cima de la montaña para sus turnos en el telescopio. Humason se interesó por el trabajo de los astrónomos y, después de casarse con la hija del electricista del observatorio, tomó allí un trabajo de conserje. Después de un tiempo, se convirtió en asistente nocturno, ayudando a los astrónomos a ejecutar el telescopio y registrar datos. Eventualmente, dejó tal huella que se convirtió en astrónomo de pleno derecho en el observatorio.
A finales de la década de 1920, Humason estaba colaborando con el Hubble fotografiando los espectros de galaxias débiles con el telescopio de 2.5 metros. (Para entonces, no había duda de que las nebulosas espirales eran de hecho galaxias). Hubble había encontrado formas de mejorar la precisión de las estimaciones de distancias a galaxias espirales, y pudo medir galaxias mucho más débiles y distantes de las que Slipher pudo observar con su telescopio mucho más pequeño. Cuando Hubble colocó sus propias estimaciones de distancia junto a las mediciones de las velocidades de recesión (la velocidad con la que se alejaban las galaxias), encontró algo impresionante: había una relación entre distancia y velocidad para las galaxias. Cuanto más distante estaba la galaxia, más rápido se alejaba de nosotros.
En 1931, Hubble y Humason publicaron conjuntamente el artículo seminal donde compararon distancias y velocidades de galaxias remotas que se alejaban de nosotros a velocidades de hasta 20,000 kilómetros por segundo y pudieron demostrar que las velocidades de recesión de las galaxias son directamente proporcionales a sus distancias de nosotros (Figura\(\PageIndex{3}\)), tal como había sugerido Lemaître.
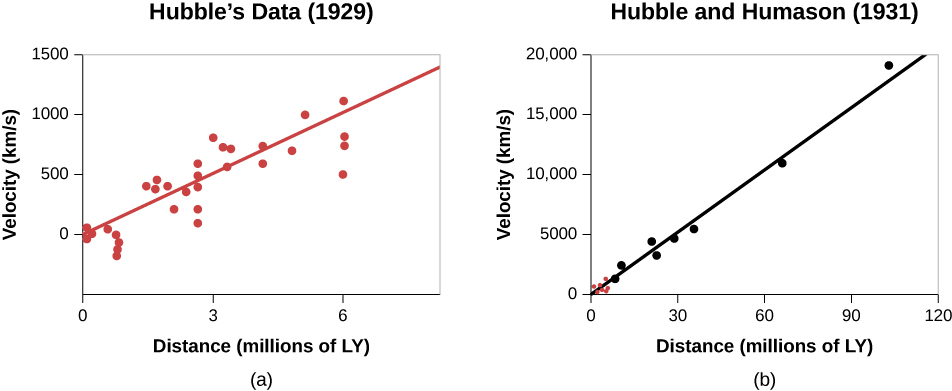
Ahora sabemos que esta relación se mantiene para cada galaxia excepto algunas de las más cercanas. Casi todas las galaxias que se acercan a nosotros resultan formar parte del propio grupo de galaxias de la Vía Láctea, que tienen sus propios movimientos individuales, así como las aves que vuelan en un grupo pueden volar en direcciones ligeramente diferentes a velocidades ligeramente diferentes a pesar de que toda la bandada viaja por el espacio juntos.
Escrito como una fórmula, la relación entre velocidad y distancia es
\[v=H \times d \nonumber\]
donde\(v\) está la velocidad de recesión,\(d\) es la distancia, y\(H\) es un número llamado la constante del Hubble. Esta ecuación se conoce ahora como ley del Hubble.
Constantes de proporcionalidad
Las relaciones matemáticas como la ley de Hubble son bastante comunes en la vida. Por tomar un ejemplo sencillo, suponga que tu colegio o universidad te contrata para llamar a ex alumnos ricos y pedir donaciones. Se te paga $2.50 por cada convocatoria; cuantas más llamadas puedas meter entre estudiar astronomía y otros cursos, más dinero te llevarás a casa. Podemos configurar una fórmula que conecte\(p\), su pago y\(n\), el número de llamadas
\[p=A \times n \nonumber\]
donde\(A\) está la constante de los alumnos, con un valor de $2.50. Si haces 20 llamadas, ganarás $2.50 veces 20, o $50.
Supongamos que tu jefe se olvida de decirte lo que te van a pagar por cada llamada. Puedes calcular la constante de ex alumnos que gobierna tu paga haciendo un seguimiento de cuántas llamadas haces y anotando tu salario bruto cada semana. Si haces 100 llamadas la primera semana y te pagan $250, puedes deducir que la constante es de $2.50 (en unidades de dólares por llamada). Hubble, por supuesto, no tenía “jefe” que le dijera cuál sería su constante: tenía que calcular su valor a partir de las medidas de distancia y velocidad.
Los astrónomos expresan el valor de la constante del Hubble en unidades que se relacionan con la forma en que miden la velocidad y la velocidad de las galaxias. En este libro, utilizaremos kilómetros por segundo por millón de años luz como esa unidad. Desde hace muchos años, las estimaciones del valor de la constante del Hubble han estado en el rango de 15 a 30 kilómetros por segundo por millón de años luz El trabajo más reciente parece estar convergiendo en un valor cercano a los 22 kilómetros por segundo por millón de años luz Si\(H\) es de 22 kilómetros por segundo por millón luz -años, una galaxia se aleja de nosotros a una velocidad de 22 kilómetros por segundo por cada millón de años luz de su distancia. Como ejemplo, una galaxia a 100 millones de años luz de distancia se está alejando de nosotros a una velocidad de 2200 kilómetros por segundo.
La ley del Hubble nos dice algo fundamental sobre el universo. Dado que todas menos las galaxias más cercanas parecen estar en movimiento lejos de nosotros, con las más distantes moviéndose más rápido, debemos estar viviendo en un universo en expansión. En breve exploraremos las implicaciones de esta idea, así como en los capítulos finales de este texto. Por ahora, solo diremos que la observación de Hubble subyace en todas nuestras teorías sobre el origen y evolución del universo.
Ley y distancias del Hubble
La regularidad expresada en la ley del Hubble tiene un bono incorporado: nos da una nueva forma de determinar las distancias a galaxias remotas. Primero, debemos establecer de manera confiable la constante del Hubble midiendo tanto la distancia como la velocidad de muchas galaxias en muchas direcciones para estar seguros de que la ley del Hubble es verdaderamente una propiedad universal de las galaxias. Pero una vez que hemos calculado el valor de esta constante y estamos satisfechos de que se aplica en todas partes, mucho más del universo se abre para la determinación de la distancia. Básicamente, si podemos obtener un espectro de una galaxia, podemos decir de inmediato qué tan lejos está.
El procedimiento funciona así. Utilizamos el espectro para medir la velocidad con la que la galaxia se aleja de nosotros. Si entonces ponemos esta velocidad y la constante del Hubble en la ecuación de la ley del Hubble, podemos resolver por la distancia.
Ejemplo\(\PageIndex{1}\): ley de hubble
La ley del Hubble (\(v = H \times d\)) nos permite calcular la distancia a cualquier galaxia. Así es como lo usamos en la práctica.
Hemos medido la constante de Hubble en 22 km/s por millón de años luz. Esto significa que si una galaxia está a 1 millón de años luz más lejos, se alejará 22 km/s más rápido. Entonces, si encontramos una galaxia que se aleja a 18,000 km/s, ¿qué nos dice la ley del Hubble sobre la distancia a la galaxia?
Solución
\[d = \frac{v}{H} = \frac{18,000 \text{ km/s}}{ \frac{22 \text{ km/s}}{1 \text{ million light-years}}} = \frac{18,000}{22} \times \frac{1 \text{ million light-years}{1} = 818 \text{ million light-years} \nonumber\]
Observe cómo manejamos las unidades aquí: los km/s en el numerador y el denominador cancelan, y el factor de millones de años luz en el denominador de la constante deben dividirse correctamente antes de obtener nuestra distancia de 818 millones de años luz.
Ejercicio\(\PageIndex{1}\)
Usando 22 km/s/millón de años luz para la constante del Hubble, ¿qué velocidad recesional esperamos encontrar si observamos una galaxia a 500 millones de años luz?
- Responder
-
\[v=d \times H = 500 \text{ million light-years} \times \frac{22 \text{ km/s}}{1 \text{ million light-years}} = 11,000 \text{ km/s} \nonumber\]
Variación de la Constante de Hubble
El uso del corrimiento al rojo es potencialmente una técnica muy importante para determinar distancias porque, como hemos visto, la mayoría de nuestros métodos para determinar distancias de galaxias están limitados aproximadamente a los pocos cientos de millones de años luz más cercanos (y tienen grandes incertidumbres a estas distancias). El uso de la ley de Hubble como indicador de distancia requiere solo un espectro de una galaxia y una medición del desplazamiento Doppler, y con grandes telescopios y espectrógrafos modernos, se pueden tomar espectros de galaxias extremadamente débiles.
Pero, como suele ocurrir en la ciencia, las cosas no son tan simples. Esta técnica funciona si, y sólo si, la constante del Hubble ha sido verdaderamente constante a lo largo de toda la vida del universo. Cuando observamos galaxias a miles de millones de años luz de distancia, las estamos viendo como estaban hace miles de millones de años. ¿Y si la “constante” del Hubble fuera diferente hace miles de millones de años? Antes de 1998, los astrónomos pensaban que, aunque el universo se está expandiendo, la expansión debería estar desacelerándose, o desacelerándose, porque la atracción gravitacional general de toda la materia en el universo tendría un efecto dominante y medible. Si la expansión se está desacelerando, entonces la constante del Hubble debería ir disminuyendo con el tiempo.
El descubrimiento de que las supernovas tipo Ia son bombillas estándar dio a los astrónomos la herramienta que necesitaban para observar galaxias extremadamente distantes y medir la tasa de expansión hace miles de millones de años. Los resultados fueron completamente inesperados. ¡Resulta que la expansión del universo se está acelerando con el tiempo! Lo que hace que este resultado sea tan impresionante es que no hay forma de que las teorías físicas existentes puedan dar cuenta de esta observación. Si bien un universo desacelerante podría explicarse fácilmente por la gravedad, no había fuerza o propiedad en el universo conocida por los astrónomos que pudieran dar cuenta de la aceleración. En el capítulo de The Big Bang, veremos con más detalle las observaciones que llevaron a este resultado totalmente inesperado y exploraremos sus implicaciones para el destino final del universo.
En cualquier caso, si la constante del Hubble no es realmente una constante cuando miramos por encima de grandes tramos de espacio y tiempo, entonces el cálculo de las distancias de las galaxias usando la constante del Hubble no será exacto. Como veremos en el capítulo sobre El Big Bang, el cálculo exacto de las distancias requiere un modelo de cómo la constante del Hubble ha cambiado a lo largo del tiempo. Cuanto más lejos esté una galaxia (y cuanto más tiempo la estemos viendo), más importante es incluir los efectos del cambio en la constante del Hubble. Para galaxias dentro de unos pocos miles de millones de años luz, sin embargo, la suposición de que la constante del Hubble es realmente constante da buenas estimaciones de distancia.
Modelos para un universo en expansión
Al principio, pensando en la ley de Hubble y siendo fanático de la obra de Copérnico y Harlow Shapley, podría sorprenderte. ¿Realmente todas las galaxias se están alejando de nosotros? ¿Hay, después de todo, algo especial en nuestra posición en el universo? No te preocupes; el hecho de que las galaxias se estén alejando de nosotros y que las galaxias más distantes se alejen más rápidamente que las cercanas muestra solo que el universo se está expandiendo uniformemente.
Un universo en expansión uniforme es aquel que se está expandiendo al mismo ritmo en todas partes. En tal universo, nosotros y todos los demás observadores, sin importar dónde se encuentren, debemos observar una proporcionalidad entre las velocidades y distancias de galaxias equivalentemente remotas. (Aquí, estamos ignorando el hecho de que la constante del Hubble no es constante en todos los tiempos, pero si en algún momento dado de la evolución del universo la constante del Hubble tiene el mismo valor en todas partes, este argumento sigue funcionando).
Para ver por qué, primero imagina una regla hecha de goma estirable, con las líneas habituales marcadas a cada centímetro. Ahora supongamos que alguien con brazos fuertes agarra cada extremo de la regla y lentamente la estira para que, digamos, duplique su longitud en 1 minuto (Figura\(\PageIndex{4}\)). Considera una hormiga inteligente sentada en la marca a 2 centímetros, un punto que no está en ninguno de los extremos ni en el medio de la regla. Mide la rapidez con la que otras hormigas, sentadas a las marcas de 4, 7 y 12 centímetros, se alejan de él a medida que el gobernante se estira.
La hormiga a 4 centímetros, originalmente a 2 centímetros de nuestra hormiga, ha duplicado su distancia en 1 minuto; por lo tanto, se alejó a una velocidad de 2 centímetros por minuto. La hormiga en la marca de 7 centímetros, que originalmente estaba a 5 centímetros de nuestra hormiga, ahora está a 10 centímetros de distancia; así tuvo que moverse a 5 centímetros por minuto. El que comenzó en la marca de 12 centímetros, que estaba a 10 centímetros de distancia de la hormiga que hacía el conteo, ahora está a 20 centímetros de distancia, es decir, debió haber corrido a una velocidad de 10 centímetros por minuto. Las hormigas a diferentes distancias se alejan a diferentes velocidades, y sus velocidades son proporcionales a sus distancias (tal como lo indica la ley de Hubble para las galaxias). Sin embargo, notemos en nuestro ejemplo que todo lo que hacía el gobernante era estirarse uniformemente. Además, fíjate que ninguna de las hormigas se movía por su propia cuenta, fue el estiramiento de la regla lo que las separaba.
Ahora repitamos el análisis, pero pongamos la hormiga inteligente en alguna otra marca, digamos, en 7 o 12 centímetros. Descubrimos que, mientras la regla se estire uniformemente, esta hormiga también encuentra a todas las demás hormigas alejándose a una velocidad proporcional a su distancia. Es decir, el tipo de relación que expresa la ley del Hubble puede explicarse por un estiramiento uniforme del “mundo” de las hormigas. Y todas las hormigas en nuestro sencillo diagrama verán a las otras hormigas alejándose de ellas a medida que la regla se estira.
Para una analogía tridimensional, veamos la hogaza de pan de pasas en Figura\(\PageIndex{5}\). El chef accidentalmente ha puesto demasiada levadura en la masa, y cuando pone el pan para que suba, se duplica su tamaño durante la siguiente hora, haciendo que todas las pasas se separen más. En la figura, nuevamente recogemos una pasa representativa (que no esté en el borde ni en el centro del pan) y mostramos las distancias de ésta a varias otras en la figura (antes y después de que el pan se expanda).
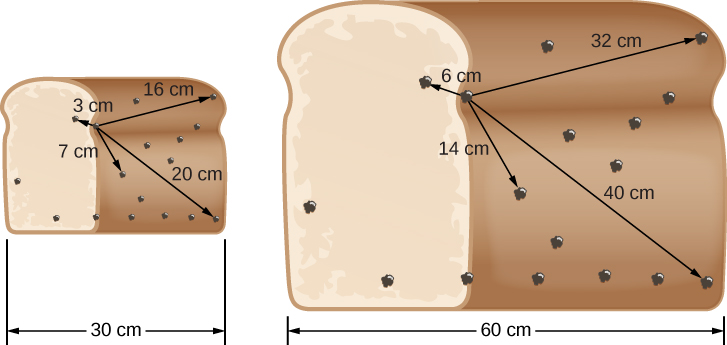
Mide los aumentos de distancia y calcula las velocidades por ti mismo en el pan de pasas, tal como hicimos para la regla. Verás que, dado que cada distancia se duplica durante la hora, cada pasa se aleja de nuestras pasas seleccionadas a una velocidad proporcional a su distancia. Lo mismo es cierto sin importar con qué pasa empieces.
Nuestras dos analogías son útiles para aclarar nuestro pensamiento, pero no debes tomarlas literalmente. Tanto en el gobernante como en el pan de pasas, hay puntos que están al final o al borde. Puedes usar estos para identificar la mitad de la regla y el pan. Si bien nuestros modelos del universo tienen cierto parecido con las propiedades del gobernante y el pan, el universo no tiene límites, ni bordes, ni centro (todas ideas alucinantes que discutiremos en un capítulo posterior).
Lo que es útil notar tanto de las hormigas como de las pasas es que ellas mismas no “causaron” su movimiento. No es como si las pasas decidieran hacer un viaje lejos unas de otras y luego se subieron a un hoverboard para escapar. No, en ambas analogías, fue el estiramiento del médium (la regla o el pan) lo que alejaba más a las hormigas o las pasas. De la misma manera, veremos en el capítulo de El Big Bang que las galaxias no tienen motores de cohetes que las propulsen lejos unas de otras. En cambio, son participantes pasivos en la expansión del espacio. A medida que el espacio se extiende, las galaxias se llevan cada vez más separadas tanto como lo fueron las hormigas y las pasas. (Si esta noción del “estiramiento” del espacio te sorprende o te molesta, ahora sería un buen momento para revisar la información sobre el espacio-tiempo en Agujeros Negros y Espacio-tiempo curvo. Discutiremos estas ideas más a medida que nuestra discusión se amplíe de galaxias a todo el universo).
La expansión del universo, por cierto, no implica que las galaxias individuales y los cúmulos de galaxias mismos se estén expandiendo. Ni las pasas ni las hormigas en nuestra analogía crecen en tamaño a medida que el pan se expande. De manera similar, la gravedad mantiene unidas las galaxias y los cúmulos de galaxias, y se alejan más entre sí, sin que ellos mismos cambien de tamaño, a medida que el universo se expande.
Resumen
El universo se está expandiendo. Las observaciones muestran que las líneas espectrales de galaxias distantes están desplazadas al rojo, y que sus velocidades de recesión son proporcionales a sus distancias de nosotros, una relación conocida como la ley del Hubble. La tasa de recesión, denominada constante del Hubble, es de aproximadamente 22 kilómetros por segundo por millón de años luz. No estamos en el centro de esta expansión: un observador en cualquier otra galaxia vería el mismo patrón de expansión que nosotros. La expansión descrita por la ley de Hubble se entiende mejor como un estiramiento del espacio.
Glosario
- Constante Hubble
- una constante de proporcionalidad en la ley que relaciona las velocidades de galaxias remotas con sus distancias
- Ley del Hubble
- una regla de que las velocidades radiales de galaxias remotas son proporcionales a sus distancias de nosotros
- corrimiento al rojo
- cuando las líneas en los espectros se desplazan hacia longitudes de onda más largas (hacia el extremo rojo del espectro visible)