2.1: La Línea Recta

Podría pensarse que hay una cantidad bastante limitada que podría escribirse sobre la geometría de una línea recta. Podemos manejar algunas Ecuaciones aquí, sin embargo, (hay 35 en esta sección de la Línea Recta) y volveremos para más sobre el tema en el Capítulo 4.

La mayoría de los lectores estarán familiarizados con la Ecuación para una línea recta:

$$y = mx + c \label{2.2.1} \tag{2.2.1}$$

La pendiente (o gradiente) de la línea, que es la tangente del ángulo que hace con el$x$ eje -es$m$, y la intersección en el$y$ eje es$c$. Existen varias otras formas que pueden ser de utilidad, como

$$\frac{x}{x_0} + \frac{y}{y_0} = 1 \label{2.2.2} \tag{2.2.2}$$

$$\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1} \label{2.2.3} \tag{2.2.3}$$

que también se puede escribir

\ begin {array} {| c c c | c}
x & y & 1\\
x_1 & y_1 & 1 & =0\\
x_2 & y_2 & 1\\
\ etiqueta {2.2.4}\ tag {2.2.4}
\ end {array}

$$x \cos \theta + y \sin \theta = p \label{2.25} \tag{2.2.5}$$

Las cuatro formas se ilustran en la figura$\text{II.1}$.

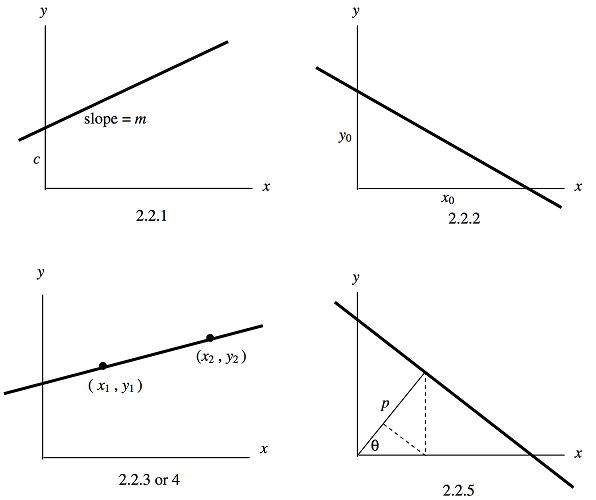
$\text{FIGURE II.1}$

También se puede escribir una línea recta en el formulario

$$Ax + By + C = 0. \label{2.2.6} \tag{2.2.6}$$

Si$C = 0$, la línea pasa por el origen. Si$C ≠ 0$, no se pierde información, y se guarda algo de aritmética y álgebra, si dividimos la ecuación\ ref {2.2.6} por$C$ y la reescribimos en la forma

$$ax + by = 1. \label{2.2.7} \tag{2.2.7}$$

Dejar$P (x , y)$ ser un punto en la línea y dejar$P_0 (x_0 , y_0 )$ ser un punto en el plano no necesariamente en la línea. Es de interés encontrar la distancia perpendicular entre$P_0$ y la línea. Dejar$S$ ser el cuadrado de la distancia entre$P_0$ y$P$. Entonces

$$S = (x-x_0)^2 + (y-y_0)^2 \label{2.2.8} \tag{2.2.8}$$

Podemos expresar esto en términos de la variable única sustituyendo$x$ por$y$ de Ecuación$\ref{2.2.7}$. Diferenciación de$S$ con respecto a$x$ mostrará entonces que$S$ es menor para

$$x = \frac{a+b(bx_0 - ay_0)}{a^2 + b^2} \label{2.2.9} \tag{2.2.9}$$

El valor correspondiente para$y$, encontrado en Ecuaciones$\ref{2.2.7}$ y$\ref{2.2.9}$, es

$$y = \frac{b+a(ay_0 - bx_0)}{a^2 + b^2}. \label{2.2.10} \tag{2.2.10}$$

El punto$\text{P}$ descrito por Ecuaciones$\ref{2.2.9}$ y$\ref{2.2.10}$ es el punto más cercano a$\text{P}_0$ en la línea. La distancia perpendicular$\text{P}$ de la línea es$p = √S$ o

$$p = \frac{1-ax_0 - by_0}{\sqrt{a^2+b^2}}. \label{2.2.11} \tag{2.2.11}$$

Esto es positivo si$\text{P}_0$ está en el mismo lado de la línea que el origen, y negativo si está en el lado opuesto. Si las distancias perpendiculares de dos puntos de la línea, calculadas a partir de la Ecuación$\ref{2.2.11}$, son de signos opuestos, están en lados opuestos de la línea. Si$p = 0$, o de hecho si el numerador de Ecuación$\ref{2.2.11}$ es cero, el punto$\text{P}_0 (x_0 , y_0 )$ está, por supuesto, en la línea.

Dejar$\text{A}(x_1 , y_1 ), \ \text{B}(x_2 , y_2 )$ y$\text{C}(x_3 , y_3 )$ ser tres puntos en el plano. ¿Cuál es el área del triángulo$\text{ABC}$? Una forma de responder a esto es sugerida por la figura$\text{II.2}$.

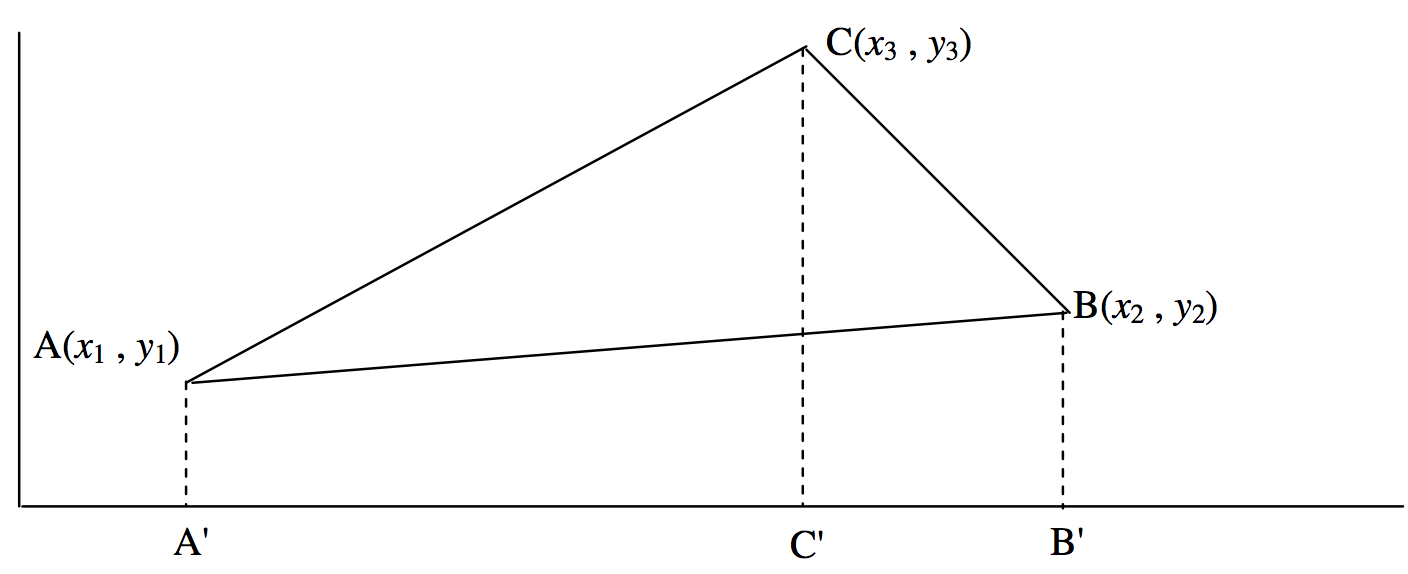
$\text{FIGURE II.2}$

Vemos que

área de triángulo$\text{ABC}$ = área de trapecio$\text{A}^\prime \text{ACC}^\prime$ (ver comentario*)
+ área de trapecio$\text{C}^\prime \text{CBB}^\prime$
− área de trapecio$\text{A}^\prime \text{ABB}^\prime$.

$$= \frac{1}{2} (x_3 - x_1) (y_3 + y_1) + \frac{1}{2} (x_2 - x_3)(y_2 + y_3) - \frac{1}{2} (x_2 - x_1) (y_2 + y_1)$$
$$= \frac{1}{2} [x_1(y_2 - y_3) + x_2 (y_3 -y_1) + x_3(y_1 - y_2)]$$

\ begin {array} {l r | c c c |}
& & x_1 & x_2 & x_3\\
= &\ frac {1} {2} & y_1 & y_2 & y_3\\
& & 1 & 1 & 1 & 1\
\ etiqueta {2.2.12}\ tag {2.2.12}
\ end {array}

* Desde que escribí esta sección me he dado cuenta de una diferencia en los usos estadounidenses y británicos de la palabra “trapecio”. Al parecer en el uso británico, “trapecio” significa un cuadrilátero con dos lados paralelos. En el uso estadounidense, un trapecio significa un cuadrilátero sin lados paralelos, mientras que un cuadrilátero con dos lados paralelos es un “trapecio”. Como ocurre con muchas palabras, los usos británicos o estadounidenses pueden ser escuchados en Canadá. En la derivación anterior, pretendía el uso británico. Lo que hay que aprender de esto es que siempre debemos cuidar de hacernos entender claramente al usar palabras tan ambiguas, y no asumir que el lector las interpretará de la manera que pretendemos.

Al lector le gustaría trabajar a través de un método alternativo, utilizando resultados que hemos obtenido anteriormente. Se obtendrá el mismo resultado. En caso de que el álgebra resulte un poco tedioso, se puede encontrar más fácil trabajar a través de un ejemplo numérico, como: calcular el área del triángulo$\text{ABC}$, donde$\text{A}$,$\text{B}$,$\text{C}$ son los puntos (2,3), (7,4), (5,6) respectivamente. En el segundo método, observamos que el área de un triángulo es$\frac{1}{2} \times \text{base} \times \text{height}$. Así, si podemos encontrar la longitud del lado BC, y la distancia perpendicular de$\text{A}$ desde$\text{BC}$, podemos hacerlo. El primero es fácil:

$$(\text{BC})^2 = (x_3 - x_2)^2 + (y_3 - y_2)^2 . \label{2.2.13} \tag{2.2.13}$$

Para encontrar la segunda, podemos escribir fácilmente la Ecuación a la línea$\text{BC}$ de Ecuación$\ref{2.2.3}$, y luego volver a escribirla en la forma$\ref{2.2.7}$. Entonces Ecuación nos$\ref{2.2.11}$ permite encontrar la distancia perpendicular de$\text{A}$ desde$\text{BC}$, y el resto es fácil.

Si el determinante en Ecuación$\ref{2.2.12}$ es cero, el área del triángulo es cero. Esto significa que los tres puntos son colineales.

El ángulo entre dos líneas

$$y = m_1 x + c_1 \label{2.2.14} \tag{2.2.14}$$

y $$y = m_2 x + c_2 \label{2.2.15} \tag{2.2.15}$$

se encuentra fácilmente recordando que los ángulos que hacen con el$x$ eje son$\tan^{-1} \ m_1$ y$\tan^{-1} \ m_2$ junto con la fórmula de trigonometría elemental$\tan( A − B) = (\tan A − \tan B) / (1+ \tan A \tan B)$. Entonces queda claro que la tangente del ángulo entre las dos líneas es

$$\frac{m_2 - m_1}{1+ m_1 m_2} . \label{2.2.16} \tag{2.2.16}$$

Las dos líneas están en ángulo recto entre sí si

$$m_1 m_2 = -1 \label{2.2.17} \tag{2.2.17}$$

La línea que biseca el ángulo entre las líneas es el lugar de puntos que son equidistantes de las dos líneas. Por ejemplo, considere las dos líneas

$$-2x + 5y = 1 \label{2.2.18} \tag{2.2.18}$$

$$30x - 10y = 1 \label{2.2.19} \tag{2.2.19}$$

Haciendo uso de la Ecuación$\ref{2.2.11}$, vemos que un punto$(x , y)$ es equidistante de estas dos líneas si

$$\frac{1+2x-5y}{\sqrt{29}} = \pm \frac{1-30x+10y}{\sqrt{1000}}. \label{2.2.20} \tag{2.2.20}$$

El significado de la$\pm$ voluntad se hará evidente en breve. Las opciones + y − resultan, respectivamente, en

$$-8.568x + 8.079y = 1 \label{2.2.21} \tag{2.2.21}$$

y $$2.656x + 2.817y = 1. \label{2.2.22} \tag{2.2.22}$$

Las dos líneas continuas en la figura$\text{II.3}$ son las líneas$\ref{2.2.18}$ y$\ref{2.2.19}$. Hay dos bisectores, representados por Ecuaciones$\ref{2.2.21}$ y$\ref{2.2.22}$, mostrados como líneas punteadas en la figura, y están en ángulo recto entre sí. La elección del signo + en Ecuación$\ref{2.2.20}$ (que en este caso resulta en Ecuación$\ref{2.2.21}$, la bisectriz en figura$\text{II.3}$ con la pendiente positiva) da la bisectriz del sector que contiene el origen.

Una ecuación de la forma

$$ax^2 + 2hxy + by^2 = 0 \label{2.2.23} \tag{2.2.23}$$

se puede factorizar en dos factores lineales sin término constante y, por lo tanto, representa dos líneas que se cruzan en el origen. Se deja como un ejercicio para determinar los ángulos que las dos líneas hacen entre sí y con el$x$ eje, y para mostrar que las líneas

$$x^2 + \left( \frac{a-b}{h} \right) xy - y^2 = 0 \label{2.2.24} \tag{2.2.24}$$

son los bisectores de$\ref{2.2.23}$ y son perpendiculares entre sí.

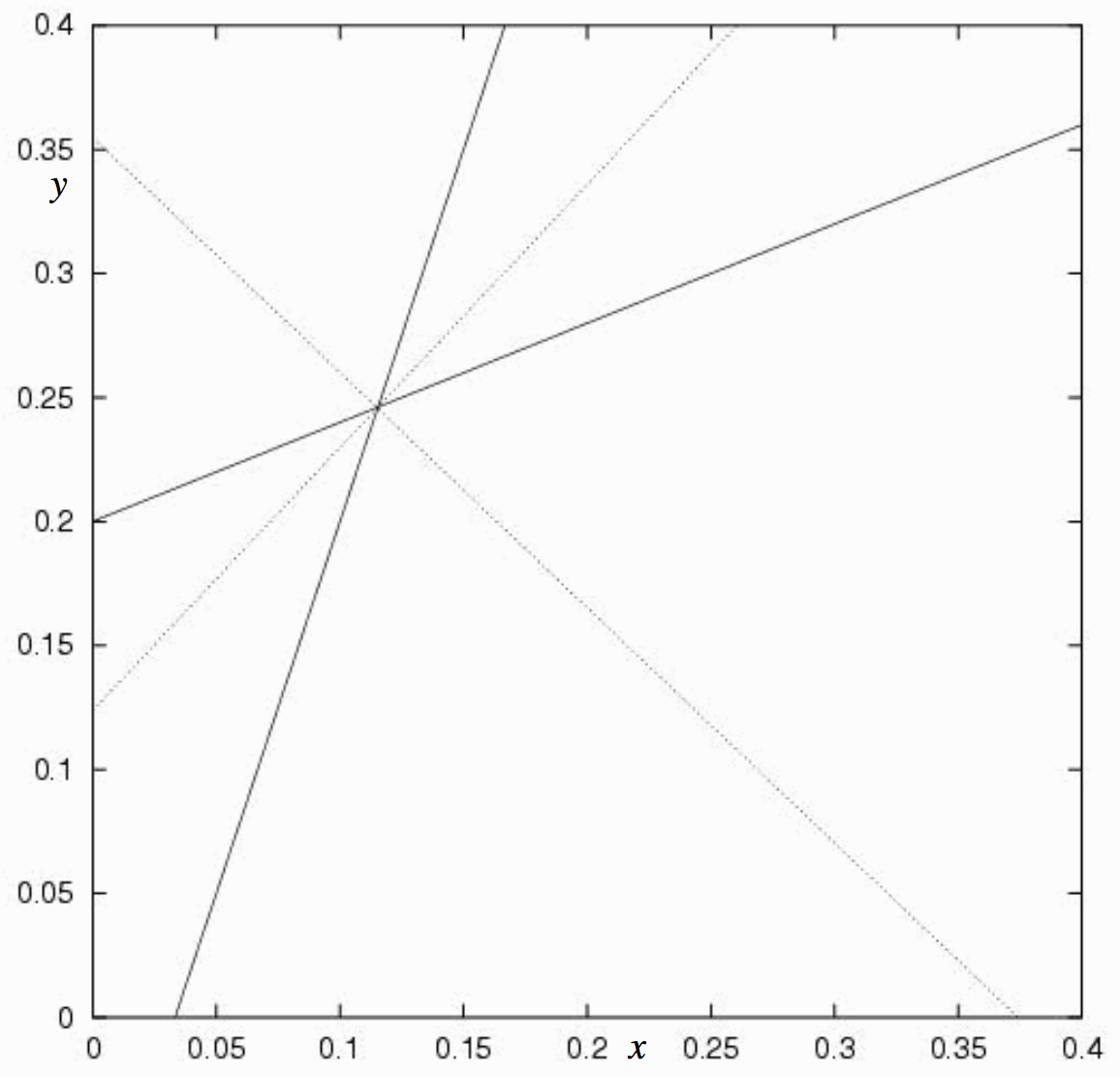
$\text{FIGURE II.3}$

Dadas las Ecuaciones a tres líneas rectas, ¿podemos encontrar el área del triángulo delimitada por ellas? Encontrar una expresión algebraica general puede ser un poco tedioso, aunque al lector le gustaría probarla, pero un ejemplo numérico es sencillo. Por ejemplo, considere las líneas

$$x - 5y + 12 = 0, \label{2.2.25} \tag{2.2.25}$$

$$3x + 4y - 9 = 0, \label{2.2.26} \tag{2.2.26}$$

$$3x - y - 3 = 0. \label{2.2.27} \tag{2.2.27}$$

Al resolver las Ecuaciones en pares, pronto se encuentra que se cruzan en los puntos (−0.15789, 2.36842), (1.4, 1.2) y (1.92857, 2.78571). La aplicación de la Ecuación da$\ref{2.2.12}$ entonces el área como 1.544. El triángulo se dibuja en la figura$\text{II.4}$. Mida cualquier lado y la altura correspondiente con una regla y vea si el área es de hecho alrededor de 1.54.

Pero ahora consideremos las tres líneas

$$x - 5y + 12 = 0, \label{2.2.28} \tag{2.2.28}$$

$$3x + 4y - 9 = 0 , \label{2.2.29} \tag{2.2.29}$$

$$3x + 23y - 54 = 0. \label{2.2.30} \tag{2.2.30}$$

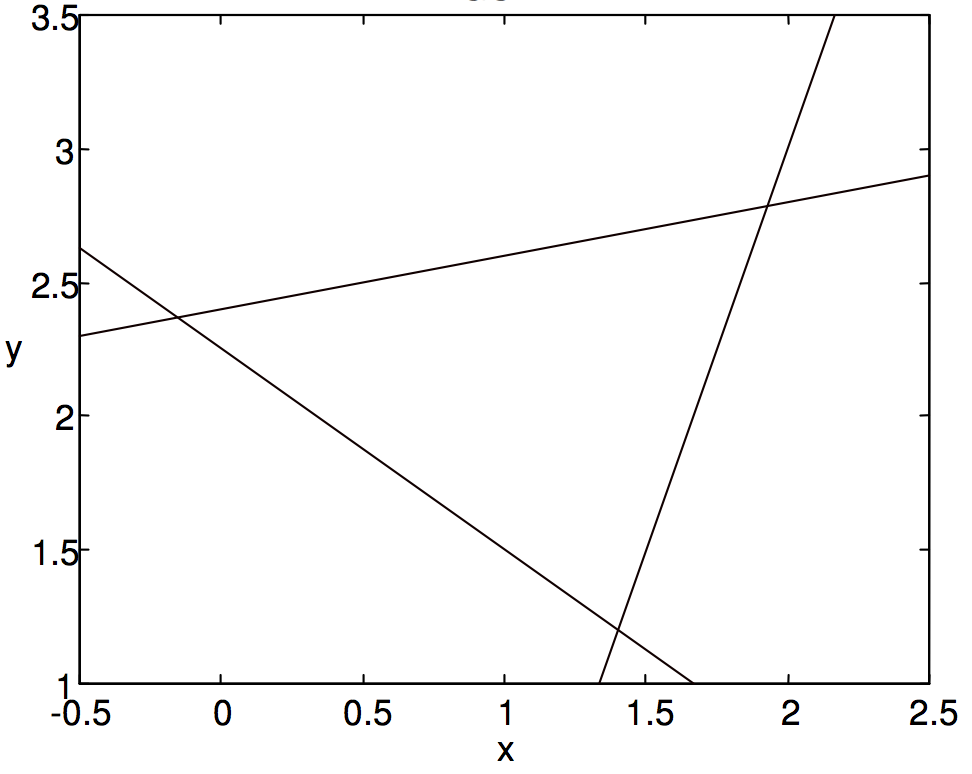
$\text{FIGURE II.4}$

Al resolver las Ecuaciones en pares, se encontrará que las tres líneas se cruzan en un mismo punto (por favor haga esto), y el área del triángulo es, por supuesto, cero. Cualquiera de estas Ecuaciones es, de hecho, una combinación lineal de las otras dos. Debe dibujar estas tres líneas con precisión en papel cuadriculado (o por computadora). En general, si tres líneas son

$$A_1 x + B_1 y + C_1 = 0 \label{2.2.31} \tag{2.2.31}$$

$$A_2 x + B_2y + C_2 = 0 \label{2.2.32} \tag{2.2.32}$$

$$A_3 x + B_3 y + C_3 = 0 \label{2.2.33} \tag{2.2.33}$$

serán concurrentes en un solo punto si

\ begin {array} {| c c c | c}
A_1 & B_1 & C_1\\
A_2 & B_2 & C_2 & = 0. \\
A_3 y B_3 y C_3\
\ etiqueta {2.2.34}\ tag {2.2.34}
\ end {array}

Así, el determinante en Ecuación$\ref{2.2.12}$ proporciona una prueba de si tres puntos son colineales, y el determinante en Ecuación$\ref{2.2.34}$ proporciona una prueba de si tres líneas son concurrentes.

Finalmente -al menos para el presente capítulo- puede haber rara ocasión de escribir la Ecuación de una línea recta en coordenadas polares. Debe ser evidente a partir de la figura$\text{II.5}$ que las Ecuaciones

$$r = p \csc (\theta - \alpha) \ \text{or} \ r = p \csc (\alpha - \theta) \label{2.2.35} \tag{2.2.35}$$

describir una línea recta que pasa a una$p$ distancia del poste y que forma un ángulo$\alpha$ con la línea inicial. Si$p = 0$, la Ecuación polar es meramente$\theta = \alpha$.

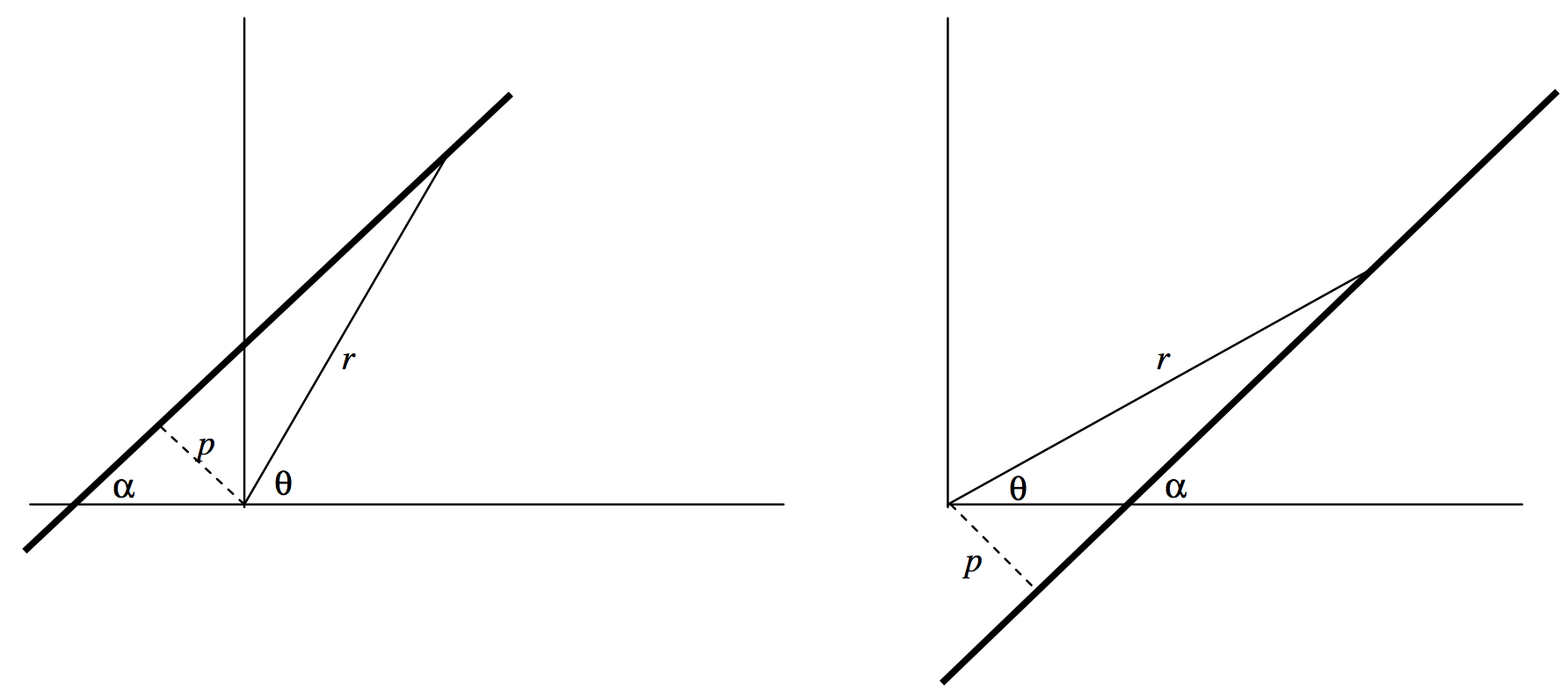
$\text{FIGURE II.5}$