2.2: La elipse

Una elipse es una figura que se puede dibujar pegando dos alfileres en una hoja de papel, atando un largo de cuerda a los alfileres, estirando la cuerda tensa con un lápiz y dibujando la figura que resulta. Durante este proceso, la suma de las dos distancias del lápiz a un alfiler y del lápiz al otro alfiler permanece constante e igual a la longitud de la cuerda. Este método de dibujar una elipse nos proporciona una definición formal, que adoptaremos en este capítulo, de elipse, a saber:

Una elipse es el locus de un punto que se mueve de tal manera que la suma de sus distancias desde dos puntos fijos llamados focos es constante (ver figura II.6).

\(\text{FIGURE II.6}\)

Llamaremos a la suma de estas dos distancias (es decir, la longitud de la cuerda)\(2a\). La relación de la distancia entre los focos a la longitud de la cuerda se llama la excentricidad\(e\) de la elipse, de manera que la distancia entre los focos es\(2ae\), y\(e\) es un número entre 0 y 1.

El eje más largo de la elipse es su eje mayor, y un poco de pensamiento mostrará que su longitud es igual a la longitud de la cuerda; es decir,\(2a\). El eje más corto es el eje menor, y su longitud suele ser denotada por\(2b\). La excentricidad está relacionada con la relación de una\(b/a\) manera que discutiremos en breve.

La relación

\[η = (a − b)/a\]

se llama elipticidad si la elipse. No es más que una medida alternativa de la no circularidad. Está relacionado con la excentricidad, y en breve también obtendremos esa relación. Hasta entonces, la Figura\(\text{II.7}\) muestra pictóricamente la relación entre ambos.

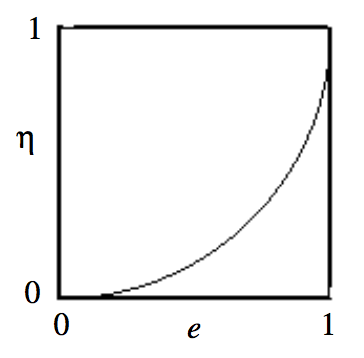
\(\text{FIGURE II.7}\)

Utilizaremos nuestra definición de elipse para obtener su Ecuación en coordenadas rectangulares. Colocaremos los dos focos en el\(x\) eje -en las coordenadas (−\(ae\), 0) y (\(ae\), 0) (véase la figura II.8).

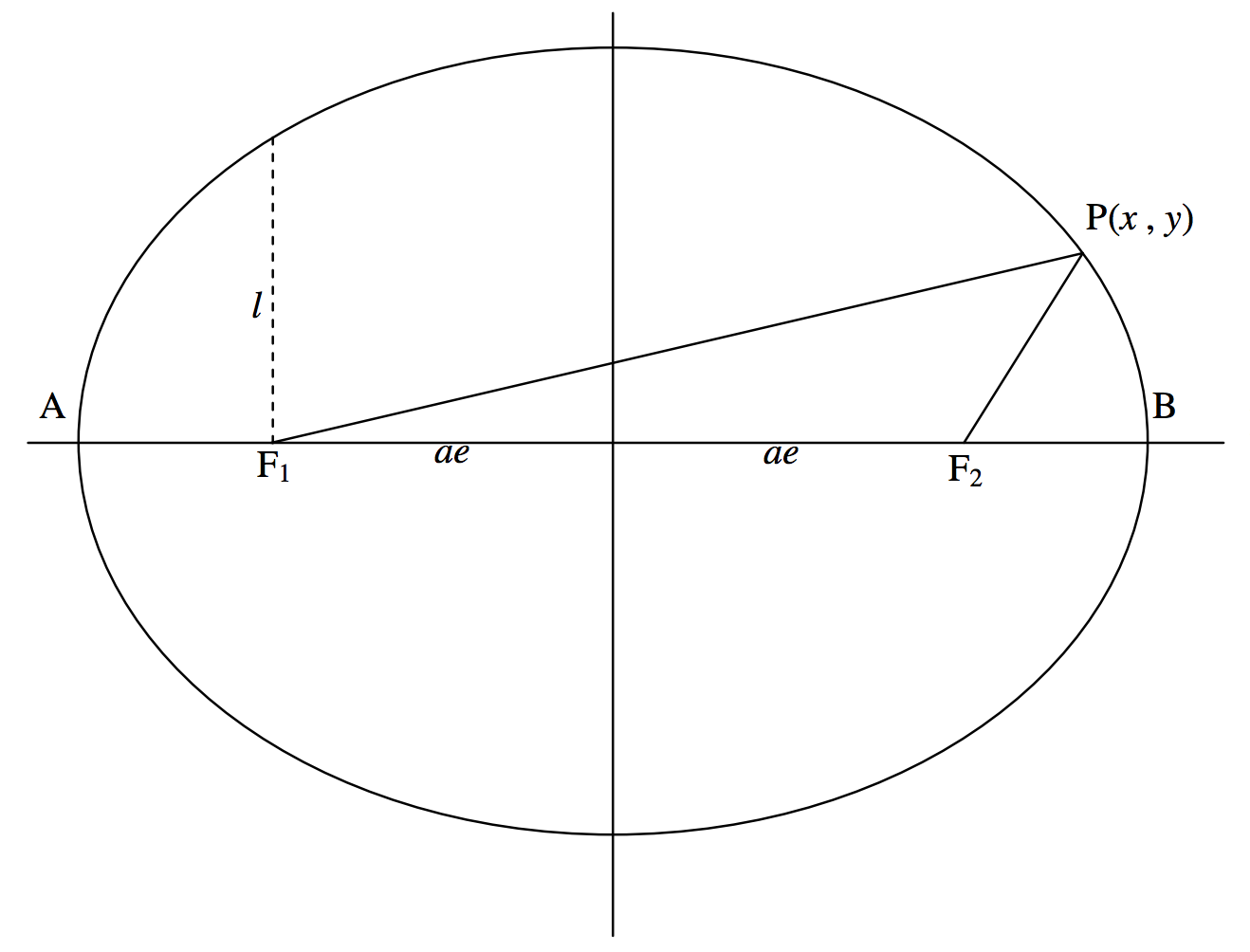
\(\text{FIGURE II.8}\)

Eso lo requiere la definición\(\textbf{PF}_1 + \textbf{PF}_2 = 2a\). Es decir:

\[\left[ (x + ae)^2 + y^2 \right]^{\frac{1}{2}} + \left[ (x-ae)^2 + y^2 \right]^{\frac{1}{2}} = 2a, \label{2.3.1} \tag{2.3.1}\]

y esta es la Ecuación a la elipse. El lector debería poder, después de un poco de álgebra un poco incómoda, demostrar que esto se puede escribir de manera más conveniente como

\[\frac{x^2}{a^2} + \frac{y^2}{a^2(1-e^2)} = 1 . \label{2.3.2} \tag{2.3.2}\]

Al poner\(x = 0\), se ve que la elipse se cruza con el\(y\) eje -en\(\pm a \sqrt{1-e^2}\) y por lo tanto eso\(a \sqrt{1-e^2}\) es igual al eje semi menor\(b\). Así tenemos la ecuación familiar a la elipse

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.3.3} \tag{2.3.3}\]

así como la importante relación entre\(a\),\(b\) y\(e\):

\[b^2 = a^2 (1-e^2) \label{2.3.4} \tag{2.3.4}\]

El lector también puede ahora derivar la relación entre elipticidad\(η\) y excentricidad\(e\):

\[η = 1 - \sqrt{(1-e^2)}. \label{2.3.5} \tag{2.3.5}\]

Esto también se puede escribir

\[e^2 = \sqrt{η(2-η)} \label{2.3.6} \tag{2.3.6}\]

o\[e^2 + (η -1)^2 = 1. \label{2.3.7} \tag{2.3.7}\]

Esto muestra, por cierto, que la gráfica de\(η\) versus\(e\), que hemos dibujado en la figura\(\text{II.7}\), forma parte de un círculo de radio 1 centrado en\(e = 0, \ η = 1\).

En las figuras\(\text{II.9}\) he dibujado elipses de excentricidades 0.1 a 0.9 en pasos de 0.1, y en la figura\(\text{II.10}\) I he dibujado elipses de elipticidades 0.1 a 0.9 en pasos de 0.1. Puede encontrar que la elipticidad le da una mejor idea que la excentricidad de la no circularidad de una elipse. Para un ejercicio, debes dibujar en las posiciones de los focos de cada una de estas elipses, y decidir si la excentricidad o elipticidad te da una mejor idea de la “excentricidad” de los focos. Obsérvese que las excentricidades de las órbitas de Marte y Mercurio son, respectivamente, de aproximadamente 0.1 y 0.2 (estas son las más excéntricas de las órbitas planetarias a excepción de Plutón parecido a un cometa), y es difícil para el ojo ver que se apartan en absoluto de los círculos, aunque, cuando se dibujan los focos, es obvio que los focos son “excéntricos”.

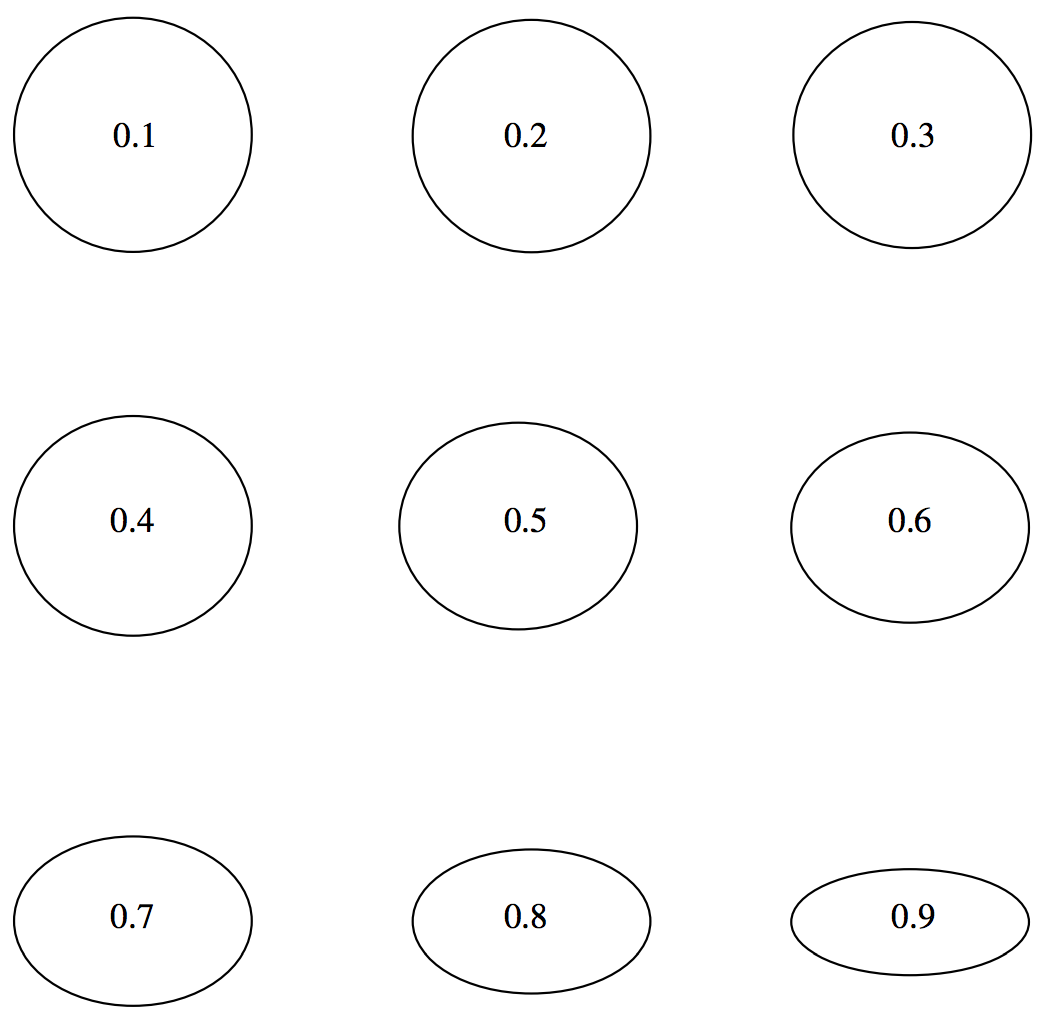
\(\text{FIGURE II.9}\): El número dentro de cada elipse es su excentricidad.

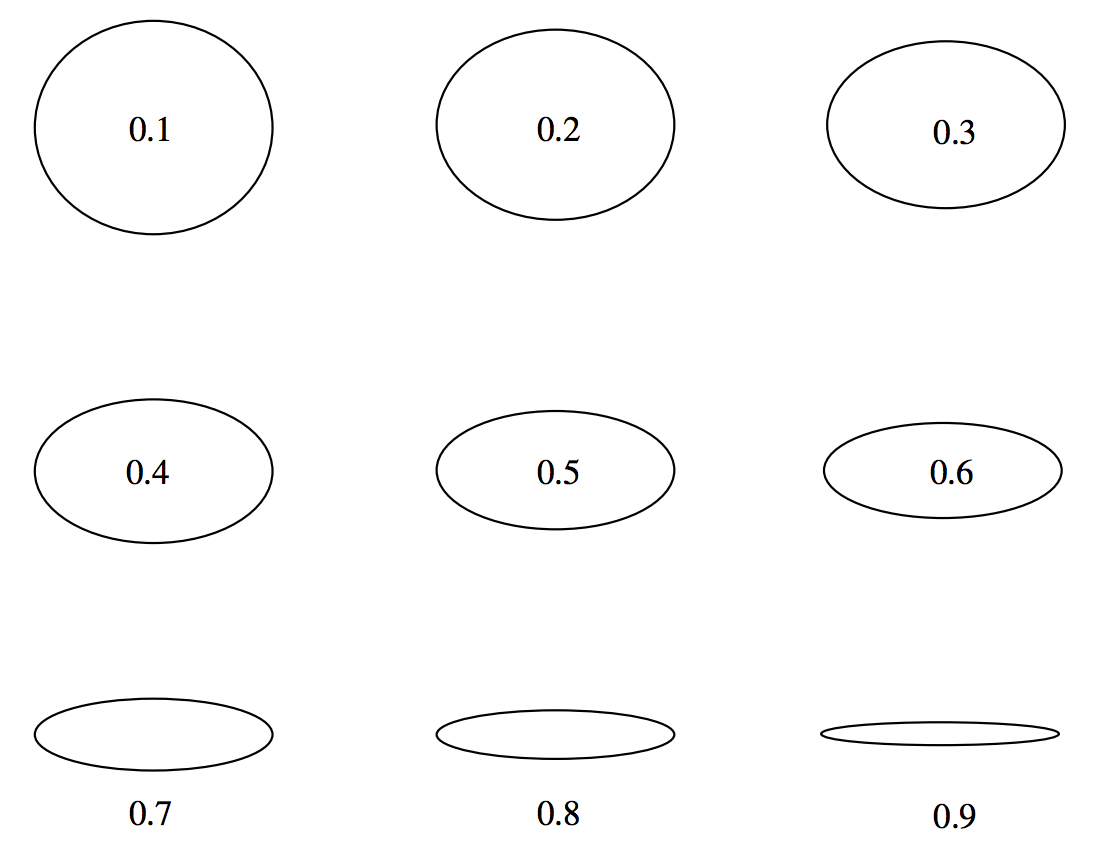
\(\text{FIGURE II.10}\): La figura dentro o debajo de cada elipse es su elipticidad.

En la teoría de las órbitas planetarias, el Sol estará en un solo foco. Supongamos que sea en\(\text{F}_2\) (ver figura\(\text{II.8}\)). En ese caso la distancia\(\text{F}_2 \ \text{B}\) es la distancia perihelio\(q\), y es igual a

\[q = a(1-e). \label{2.3.8} \tag{2.3.8}\]

La distancia\(\text{F}_2 \ \text{A}\) es la distancia de afelión Q (pronunciada afhelio por algunos y affelion por otros − y ambas tienen posiciones defendibles), y es igual a

\[Q = a(1 + e). \label{2.3.9} \tag{2.3.9}\]

Una línea paralela al eje menor y que pasa por un foco se llama recto latus (plural: latera recta). La longitud de un recto semilatoso se denota comúnmente por\(l \) (a veces por\(p\)). Su longitud se obtiene poniendo\(x = ae\) en la Ecuación a la elipse, y se encontrará fácilmente que

\[l = a(1-e^2). \label{2.3.10} \tag{2.3.10}\]

La longitud del recto semilatoso es una cantidad importante en la teoría de la órbita. Se encontrará, por ejemplo, que la energía de un planeta está estrechamente relacionada con el semieje mayor\(a\) de su órbita, mientras que su momento angular está estrechamente relacionado con el recto semi latus.

El círculo cuyo diámetro es el eje mayor de la elipse se denomina círculo excéntrico o, preferiblemente, el círculo auxiliar (figura\(\text{II.11}\)). Su Ecuación es

\[x^2 + y^2 = a^2 . \label{2.3.11} \tag{2.3.11}\]

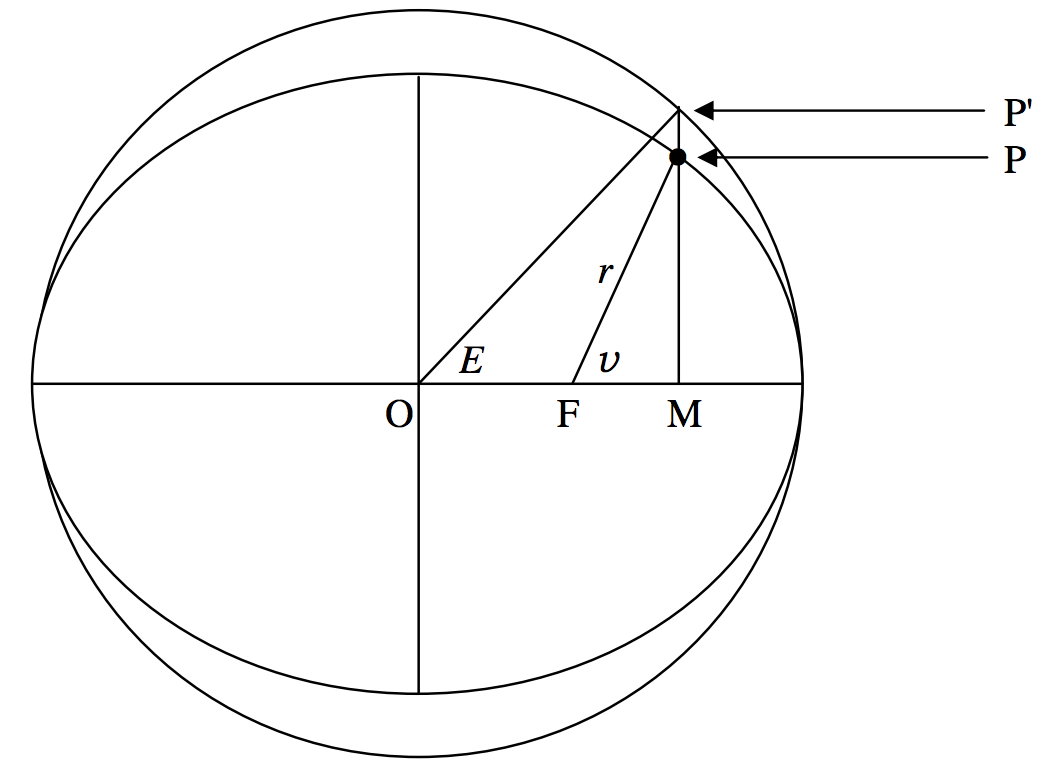
\(\text{FIGURE II.11}\)

En la teoría de la órbita el ángulo\(v\) (denotado\(f\) por algunos autores) se llama la verdadera anomalía de un planeta en su órbita. El ángulo\(E\) se llama anomalía excéntrica, y es importante encontrar una relación entre ellos.

Primero notamos que, si la anomalía excéntrica lo es\(E\), las abscisas de\(\text{P}^\prime\) y de\(\text{P}\) son cada una\(a \cos E\). La ordenada de\(\text{P}^\prime\) es\(a \sin E\). Al poner\(x = a \cos E\) en la Ecuación a la elipse, enseguida encontramos que la ordenada de\(\text{P}\) es\(b \sin E\). Siguen varias deducciones. Una es que cualquier punto cuya abscisa y ordenada sean de la forma

\[x = a \cos E , \quad y = b \sin E \label{2.3.12} \tag{2.3.12}\]

está en una elipse de semieje mayor\(a\) y semieje menor\(b\). Estas dos Ecuaciones pueden ser consideradas como ecuaciones paramétricas a la elipse. Se pueden usar para describir una elipse tan fácilmente como

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.3.13} \tag{2.3.13}\]

y de hecho esta Ecuación es el\(E\) -eliminante de las Ecuaciones paramétricas.

La relación\(\text{PM}/\text{P}^\prime \text{M}\) para cualquier línea perpendicular al eje mayor es\(b/a\). En consecuencia, el área de la elipse es\(b/a\) multiplicada por el área del círculo auxiliar; y como el área del círculo auxiliar es\(\pi a^2\), se deduce que el área de la elipse es\(\pi ab\).

En la figura\(\text{II.11}\), la distancia\(r\) se denomina vector de radio (vectores de radios plurales), y desde el teorema de Pitágoras su longitud viene dada por

\[r^2 = b^2 \sin^2 E + a^2 (\cos E - e)^2 . \label{2.3.14} \tag{2.3.14}\]

Al sustituir\(1 − \cos^2 E\) por\(\sin^2 E\) y\(a^2 (1 - e^2 )\) para\(b^2\), pronto encontramos que

\[r = a (1 - e \cos E ) \label{2.3.15} \tag{2.3.15}\]

Entonces se deduce inmediatamente que la relación deseada entre\(v\) y\(E\) es

\[\cos v = \frac{\cos E - e}{1 - e \cos E} . \label{2.3.16} \tag{2.3.16}\]

A partir de identidades trigonométricas, esto también se puede escribir

\[\sin v = \frac{\sqrt{1-e^2} \sin E}{1-e \cos E} \tag{2.3.17a} \label{2.3.17a}\]

o\[\tan v = \frac{\sqrt{1-e^2} \sin E}{\cos E - e} \label{2.3.17b} \tag{2.3.17b}\]

o\[ \tan \frac{1}{2} v = \sqrt{\frac{1+e}{1-e}} \tan \frac{1}{2} E . \label{2.3.17c} \tag{2.3.17c}\]

Las fórmulas inversas también pueden ser útiles:

\[\cos E = \frac{e+\cos v}{1+e \cos v} \label{2.3.17d} \tag{2.3.17d}\]

\[\sin E = \frac{\sin v \sqrt{1-e^2}}{e + \cos v} \label{2.3.17e} \tag{2.3.17e}\]

\[\tan E = \frac{\sin v \sqrt{1-e^2}}{e+ \cos v} \label{2.3.17f} \tag{2.3.17f}\]

\[\tan \frac{1}{2} E = \sqrt{\frac{1-e}{1+e}} \tan \frac{1}{2} v . \label{2.3.17g} \tag{2.3.17g}\]

Hay una serie de propiedades geométricas diversas de una elipse, algunas, pero no necesariamente todas, de las cuales pueden resultar de utilidad en cálculos orbitales. Describimos algunas de ellas en lo que sigue.

Tangentes a una elipse

Encuentra dónde\(y = mx + c\) intersecta la línea recta con la elipse

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 . \label{2.3.18} \tag{2.3.18}\]

La respuesta a esta pregunta se encuentra sustituyendo\(y\) en\(mx + c\) la Ecuación a la elipse. Después de algún reordenamiento, una Ecuación cuadrática\(x\) da como resultado:

\[\left(a^2 m^2 + b^2 \right) x^2 + 2a^2 cmx + a^2 \left( c^2 - b^2 \right) = 0 . \label{2.3.19} \tag{2.3.19}\]

Si esta Ecuación tiene dos raíces reales, las raíces son las\(x\) coordenadas -de los dos puntos donde la línea intersecta la elipse. Si no tiene raíces reales, la línea pierde la elipse. Si tiene dos raíces reales coincidentes, la línea es tangente a la elipse. La condición para ello se encuentra estableciendo el discriminante de la Ecuación cuadrática a cero, a partir de lo cual se encuentra que

\[c^2 = a^2 m^2 + b^2 . \label{2.3.20} \tag{2.3.20}\]

Así una línea recta de la forma

\[y = mx \pm \sqrt{a^2 m^2 + b^2} \label{2.3.21} \tag{2.3.21}\]

es tangente a la elipse.

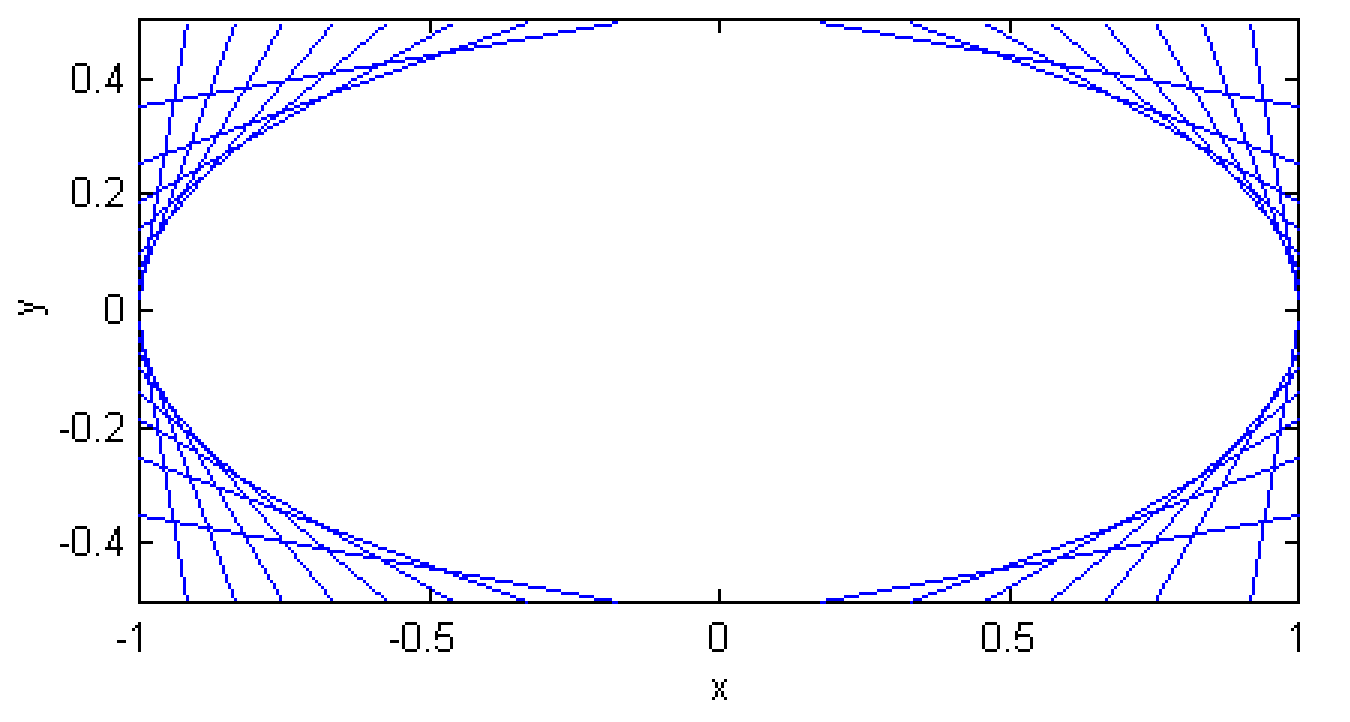
La figura\(\text{II.12}\) muestra varias de tales líneas, para\(a = 2b\) y pendientes (\(\tan^{-1} \ m)\)de\(0^\circ\) a\(180^\circ\) en pasos de\(10^\circ\)

\(\text{FIGURE II.12}\)

Círculo Director

La Ecuación que acabamos de derivar para una tangente a la elipse se puede reorganizar para leer

\[m^2 \left( a^2 - x^2 \right) + 2mx + b^2 - y^2 = 0. \label{2.3.22} \tag{2.3.22} \]

Ahora el producto de las pendientes de dos líneas que están en ángulo recto entre sí es\(−1\) (Ecuación 2.2.17). Por lo tanto, si reemplazamos\(m\) en la Ecuación anterior por\(−1/m\) obtendremos otra tangente a la elipse, en ángulo recto con la primera. La Ecuación a esta segunda tangente se convierte (después de la multiplicación a lo largo por\(m\))

\[m^2 \left( b^2 - y^2 \right) - 2mx + a^2 - x^2 = 0. \label{2.3.23} \tag{2.3.23}\]

Si eliminamos\(m\) de estas dos Ecuaciones, obtendremos una Ecuación en\(x\) y\(y\) que describe el punto donde se encuentran las dos tangentes perpendiculares; es decir, la Ecuación que describirá una curva que es el locus del punto de intersección de dos tangentes perpendiculares. Resulta que esta curva es un círculo de radio\(\sqrt{a^2 + b^2}\), y se le llama círculo director.

Es más fácil de lo que podría parecer primero eliminar\(m\) de las Ecuaciones. Simplemente tenemos que añadir las Ecuaciones\(\ref{2.3.22}\) y\(\ref{2.3.23}\):

\[m^2 \left( a^2 + b^2 - x^2 - y^2 \right) + a^2 + b^2 - x^2 - y^2 = 0 . \label{2.3.24} \tag{2.3.24}\]

De verdad\(m\), esto solo puede ser si

\[x^2 + y^2 = a^2 + b^2 , \label{2.3.25} \tag{2.3.25}\]

que es el lugar requerido del círculo director de radio\(\sqrt{a^2 + b^2}\). Se ilustra en la figura\(\text{II.13}\).

Ahora derivaremos una Ecuación a la línea que es tangente a la elipse en el punto\((x_1 , \ y_1 )\).

Dejar\((x_1 , \ y_1 ) = (a \cos E_1 , b \sin E_1 )\) y\((x_2 , \ y_2 ) = (a \cos E_2 , b \sin E_2 )\) ser dos puntos en la elipse.

La línea que une estos dos puntos es

\[\frac{y-b\sin E_1}{x-a \cos E_1} = \frac{b ( \sin E_2 - \sin E_1 )}{a(\cos E_2 - \cos E_1 )} = \frac{2b \cos \frac{1}{2}(E_2 + E_1) \sin \frac{1}{2}(E_2 - E_1)}{-2a \sin \frac{1}{2} (E_2 + E_1) \sin \frac{1}{2}(E_2 - E_1)} = -\frac{b \cos \frac{1}{2} (E_2 + E_1)}{a \sin \frac{1}{2} (E_2 + E_1)}. \label{2.3.26} \tag{2.3.26}\]

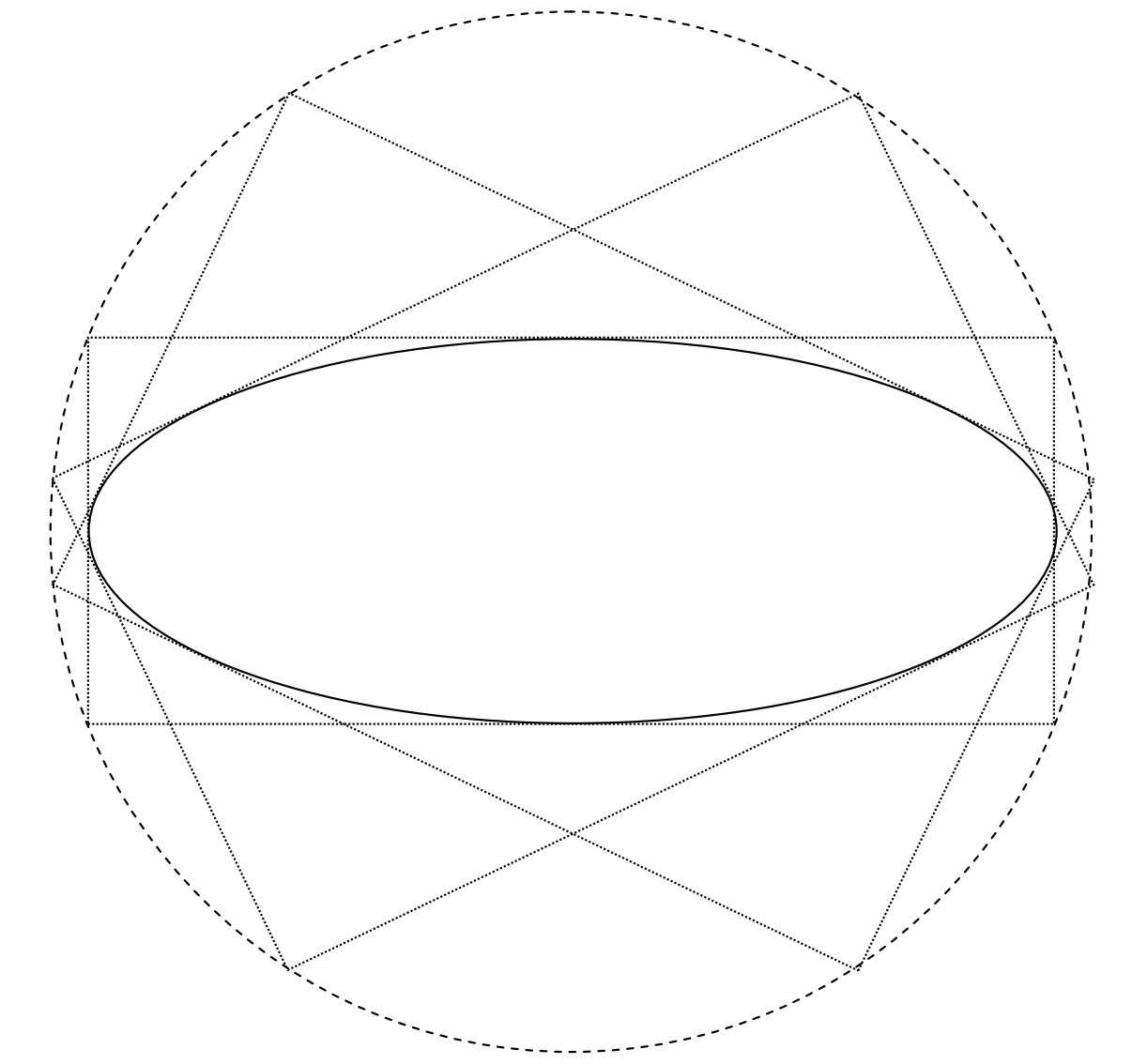
\(\text{FIGURE II.13}\)

Ahora vamos a\(E_2\) acercarnos\(E_1\), coincidiendo finalmente con él. La ecuación resultante

\[\frac{y-b\sin E}{x - a \cos E} = - \frac{b \cos E}{a \sin E} , \label{2.3.27} \tag{2.3.27}\]

en la que ya no distinguimos entre\(E_1\) y\(E_2\), es la Ecuación de la línea recta que es tangente a la elipse en\((a \cos E \ , b \sin E )\). Esto se puede escribir

\[\frac{x \cos E}{a} + \frac{y \sin E}{b} = 1 \label{2.3.28} \tag{2.3.28}\]

o, en términos de\((x_1 , \ y_1 )\),

\[\frac{x_1 x}{a^2} + \frac{y_1 y}{b^2} = 1, \label{2.3.29} \tag{2.3.29}\]

que es la tangente a la elipse en\((x_1 , \ y_1 )\).

Una propiedad interesante de una tangente a una elipse, cuya prueba dejo al lector, es esa\(\text{F}_1 \text{P}\) y\(\text{F}_2 \text{P}\) hacer ángulos iguales con la tangente at\(\text{P}\). Si el interior de la elipse fuera un espejo reflectante y se colocara una fuente puntual de luz\(\text{F}_1\), se tomaría una imagen en\(\text{F}_2\). (Echa un vistazo a la figura\(\text{II.6}\) o\(\text{II.8}\).) Esto ha tenido una interesante aplicación médica. Un paciente tiene un cálculo renal. Se le pide al paciente que se acueste en un baño elíptico, con el cálculo renal en\(\text{F}_2\). Una pequeña explosión se detona en\(\text{F}_1\); la onda de sonido explosiva que emana\(\text{F}_1\) se enfoca como una implosión\(\text{F}_2\) y el cálculo renal en\(\text{F}_2\) se rompe. No intentes esto en casa.

Direticas

Las dos líneas\(x = \pm a / e\) se llaman las directrices (directrix singular) de la elipse (figura\(\text{II.14}\)).

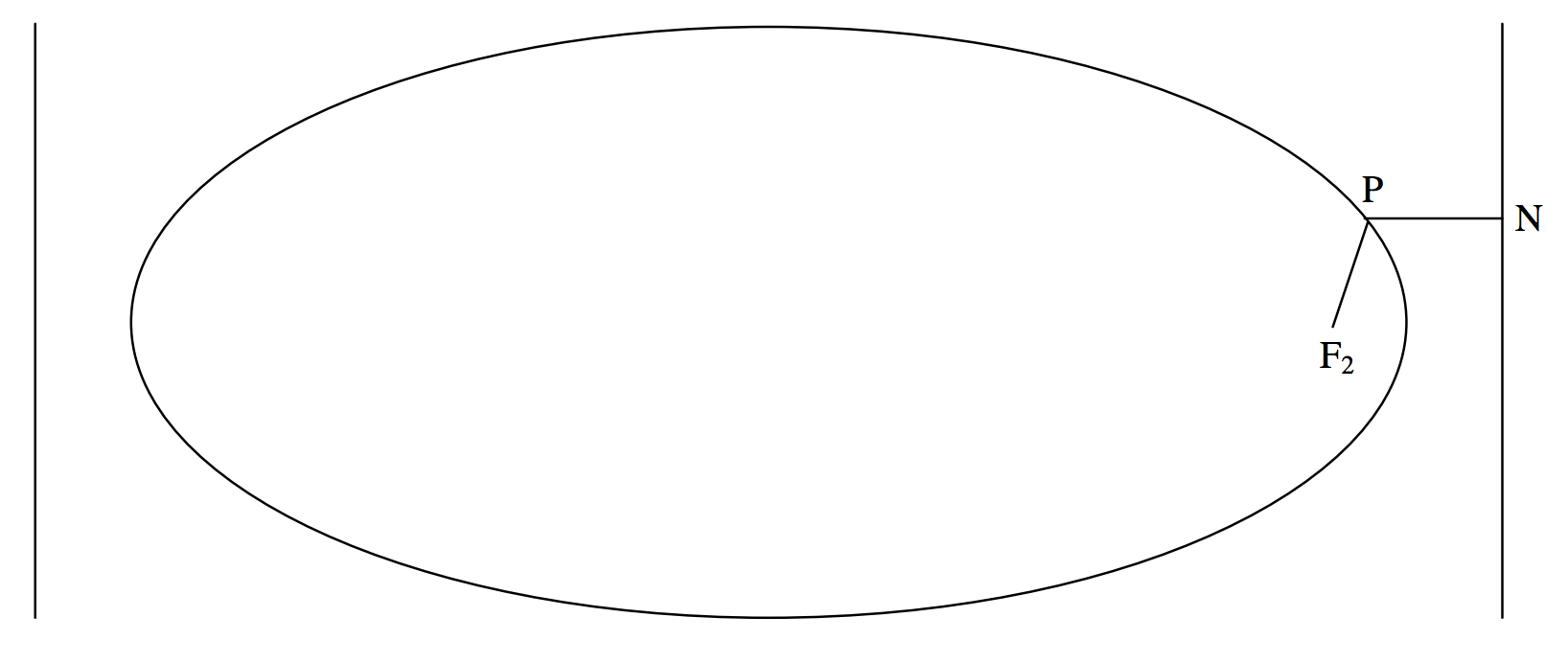
\(\text{FIGURE II.14}\)

La elipse tiene la propiedad de que, para cualquier punto\(\text{P}\) de la elipse, la relación entre la distancia\(\text{PF}_2\) a un foco y la distancia\(\text{PN}\) a una directrix es constante y es igual a la excentricidad de la elipse. En efecto, esta propiedad a veces se usa como definición de elipse, y todas las ecuaciones y propiedades que hasta ahora hemos derivado pueden deducirse de dicha definición. Nosotros, sin embargo, adoptamos una definición diferente, y se debe derivar la propiedad focus-directrix. Esto es sencillo, pues, (recordando que la abcissa de\(\text{F}_2\) es\(ae\)) vemos a partir de la figura\(\text{II.14}\) que el cuadrado de la relación deseada es

\[\frac{(x - a e)^2 + y^2}{(a/e-x)^2}. \label{2.3.30} \tag{2.3.30}\]

En sustitución de

\[b^2 \left( 1 - \left( \frac{x}{a} \right)^2 \right) = a^2 \left( 1 - e^2 \right) \left( 1 - \left( \frac{x}{a} \right)^2 \right) = \left( 1 - e^2 \right) \left( a^2 - x^2 \right) \label{2.3.31} \tag{2.3.31}\]

para\(y^2\), se ve que la expresión anterior se reduce a\(e^2\).

Otra propiedad interesante del foco y directrix, aunque una propiedad probablemente con poca aplicación a la teoría de la órbita, es que si la tangente a una elipse en un punto se\(\text{P}\) cruza con la directrix en\(\text{Q}\), entonces\(\text{P}\) y\(\text{Q}\) subtiende un ángulo recto en el foco. (Ver figura\(\text{II.15}\)).

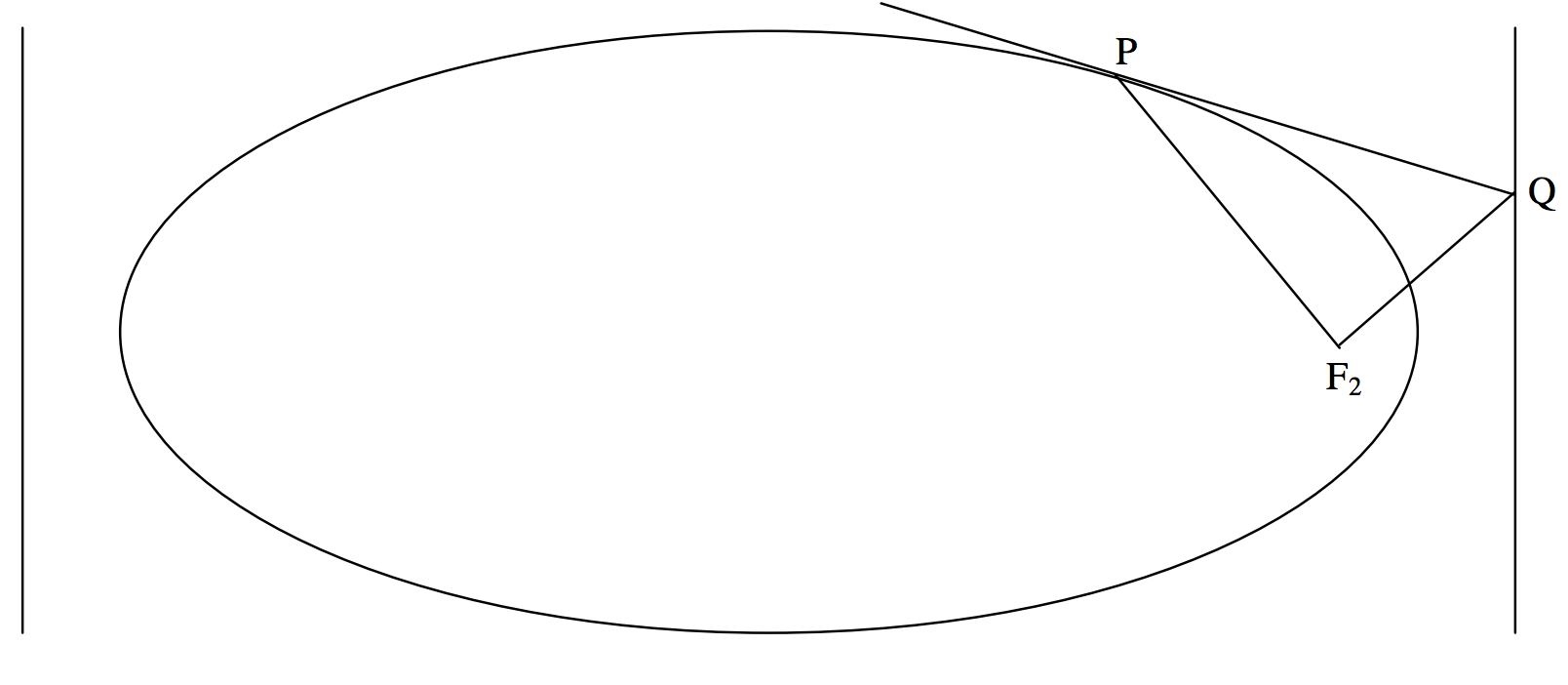
\(\text{FIGURE II.15}\)

Así la tangente a\(\text{P} = (x_1 , \ y_1 )\) es

\[\frac{x_1 x}{a^2} + \frac{y_1 y }{b^2} = 1 \label{2.3.32} \tag{2.3.32}\]

y es sencillo demostrar que se cruza con la directrix\(x = a/e\) en el punto

\[\left( \frac{a}{e} , \frac{b^2}{y_1} \left( 1 - \frac{x_1}{ae} \right) \right) . \]

Las coordenadas del foco\(\text{F}_2\) son\((ae, 0)\). La pendiente de la línea\(\text{PF}_2\) es\((x_1 - ae )/y_1\) y la pendiente de la línea\(\text{QF}_2\) es

\[\frac{\frac{b^2}{y_1} \left( 1 - \frac{x_1}{ae} \right)}{\frac{a}{e} - ae}. \]

Es fácil demostrar que el producto de estas dos pendientes es\(−1\), y de ahí eso\(\text{PF}_2\) y\(\text{QF}_2\) están en ángulo recto.

Diámetros conjugados

La izquierda de la figura\(\text{II.16}\) muestra un círculo y dos diámetros perpendiculares. La figura de la derecha muestra cómo se vería el círculo cuando se viera en algún ángulo oblicuo. El círculo se ha convertido en una elipse, y los diámetros ya no son perpendiculares. Los diámetros se denominan diámetros conjugados de la elipse. Uno es conjugado con el otro, y el otro es conjugado con el uno. Tienen la propiedad -o la definición- de que cada uno biseca todos los acordes paralelos al otro, porque esta propiedad de la bisección, que obviamente está sostenida por los diámetros perpendiculares del círculo, está inalterada en proyección.

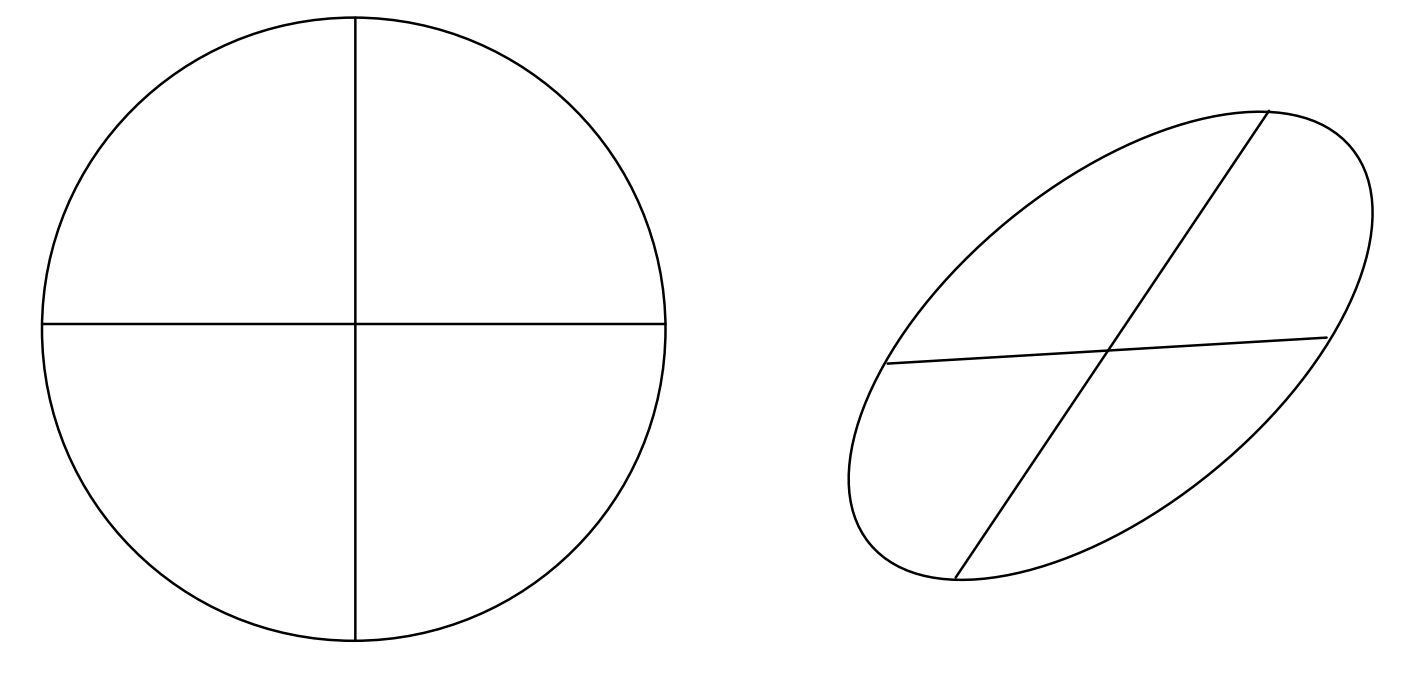
\(\text{FIGURE II.16}\)

Es fácil dibujar dos diámetros conjugados de una elipse de excentricidad\(e\) ya sea haciendo uso de esta última propiedad mencionada o señalando que es el producto de las pendientes de dos diámetros conjugados\(e^2 − 1\). La prueba de ello se deja para el disfrute del lector.

Un problema de escalera.

Ningún libro sobre matemáticas aplicadas elementales está completo sin un problema de escalera. Una escalera de longitud\(a + b\) se apoya contra una pared vertical lisa y un piso horizontal liso. Un peldaño particular se encuentra a una distancia\(a\) de la parte superior de la escalera y\(b\) de la parte inferior de la escalera. Demuestre que, cuando la escalera se desliza, el peldaño describe una elipse. (Este resultado sugerirá otra forma de dibujar una elipse). Ver figura\(\text{II.17}\).

\(\text{FIGURE II.17}\)

Si no has hecho este problema después de un minuto, aquí tienes una pista. Deja que en cualquier momento sea el ángulo que hace la escalera con el piso\(E\). Ese es el final de la pista.

El lector puede ser consciente de que algunas de las propiedades geométricas que hemos discutido en los últimos párrafos son de mayor interés recreativo y pueden no tener mucha aplicación directa en la teoría de las órbitas. En la siguiente subsección volvemos a las propiedades y Ecuaciones que son muy relevantes para la teoría orbital -quizás la más importante de todas para que la computadora de órbita la entienda.

Ecuación polar a la elipse

Obtendremos la Ecuación en coordenadas polares a una elipse cuyo foco es el polo de las coordenadas polares y cuyo eje mayor es la línea inicial\((\theta = 0^\circ )\) de las coordenadas polares. En figura\(\text{II.18}\) hemos indicado el ángulo\(\theta\) de coordenadas polares, y se le puede ocurrir al lector que previamente hemos utilizado el símbolo\(v\) para este ángulo y lo llamamos la verdadera anomalía. Efectivamente en la actualidad,\(v\) y\(\theta\) son idénticos, pero un poco más tarde vamos a distinguir entre ellos.

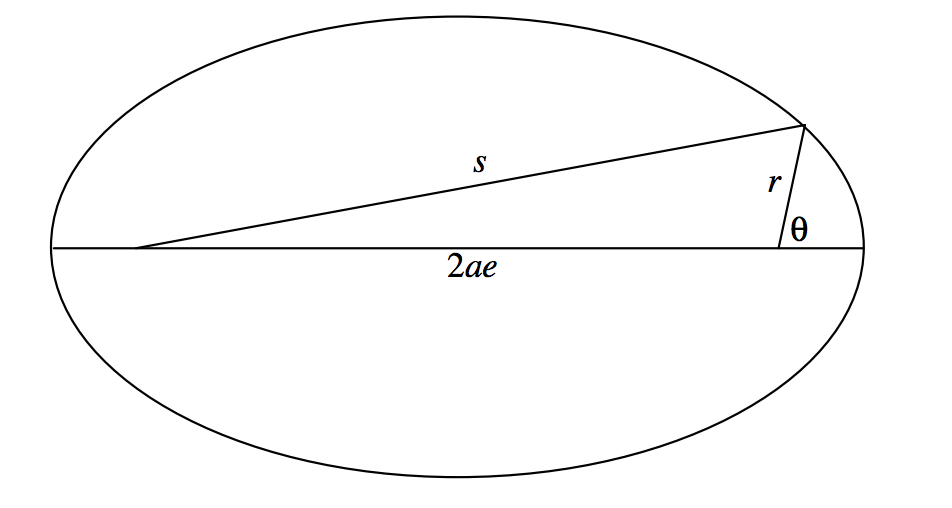
\(\text{FIGURE II.18}\)

De nuestra definición de la elipse,\(s = 2a − r\), y así

\[s^2 = 4a^2 - 4ar + r^2 . \label{2.3.33} \tag{2.3.33}\]

De la fórmula coseno para un triángulo plano,

\[s^2 = 4a^2 e^2 + r^2 + 4aer \cos \theta . \label{2.3.34} \tag{2.3.34}\]

Al igualar estas expresiones pronto obtenemos

\[a \left( 1 - e^2 \right) = r \left( 1 + e \cos \theta \right) . \label{2.3.35} \tag{2.3.35} \]

El lado izquierdo es igual al recto semi latus\(l\), y así llegamos a la Ecuación polar a la elipse, enfoque como polo, eje mayor como línea inicial:

\[r = \frac{1}{1+e \cos \theta}. \label{2.3.36} \tag{2.3.36}\]

Si el eje mayor está inclinado en un ángulo\(ω\) con respecto a la línea inicial (figura\(\text{II.19}\)), la Ecuación se convierte

\[r = \frac{l}{1 + e \cos (\theta - ω)} = \frac{l}{1+ e \cos v}. \label{2.3.37} \tag{2.3.37}\]

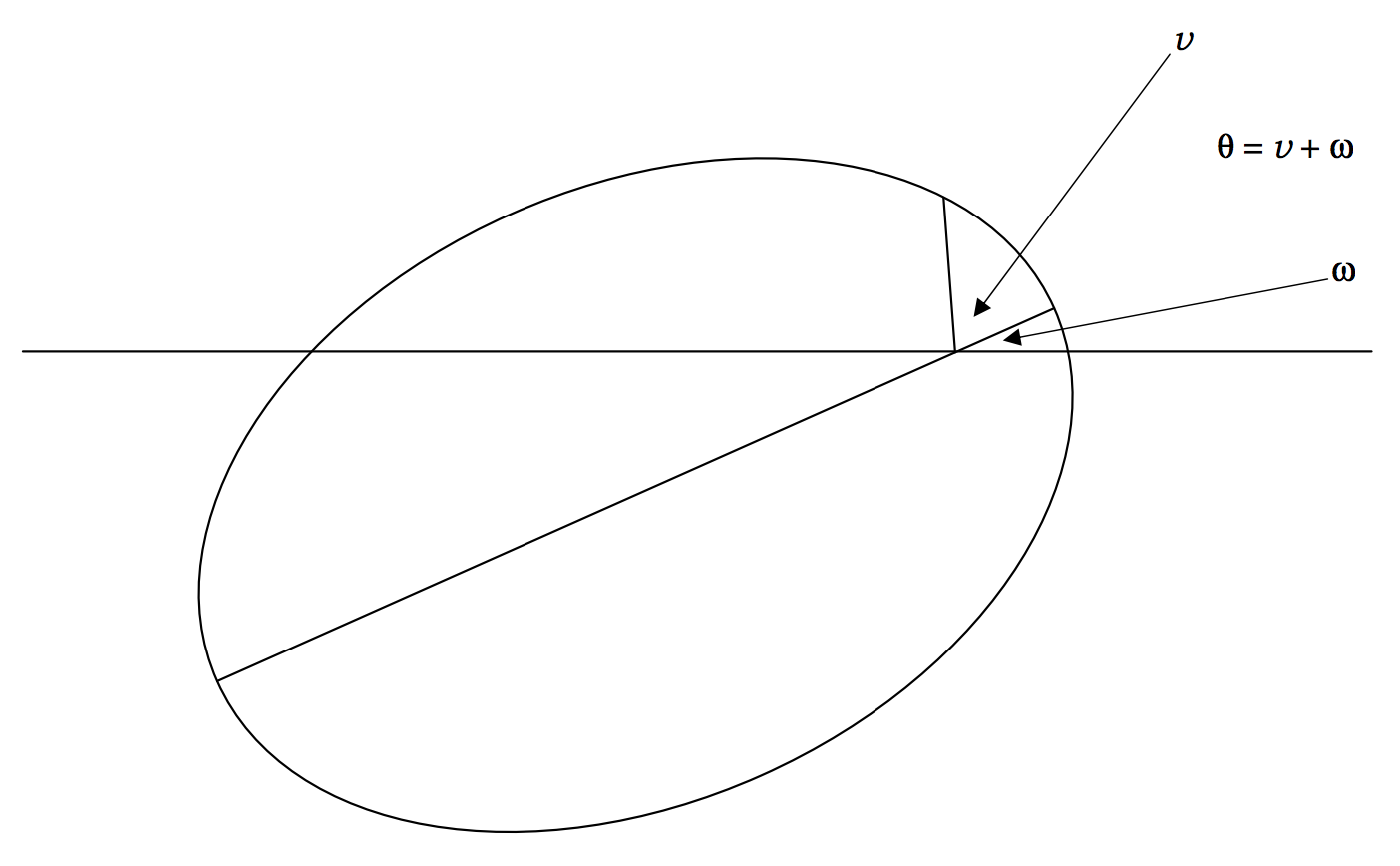
\(\text{FIGURE II.19}\)

La distinción entre\(θ\) y\(v\) es ahora evidente. \(θ\)es el ángulo de coordenadas polares,\(ω\) es el ángulo entre el eje mayor y la línea inicial (se\(ω\) denominará en teoría orbital como el “argumento del perihelio”), y\(v\), la verdadera anomalía, es el ángulo entre el radio vector y la línea inicial.