4.1: Ecuación de continuidad y las leyes de Kirchhoff
- Page ID
- 130650
Hasta este punto, nuestra discusión de los conductores se ha limitado a los casos en que están separados con aislantes (es decir, el espacio libre o algún medio dieléctrico), evitando cualquier movimiento continuo de cargas de un conductor a otro, incluso si hay un voltaje distinto de cero (y por lo tanto campo eléctrico) entre ellos — ver Fig. 1a.
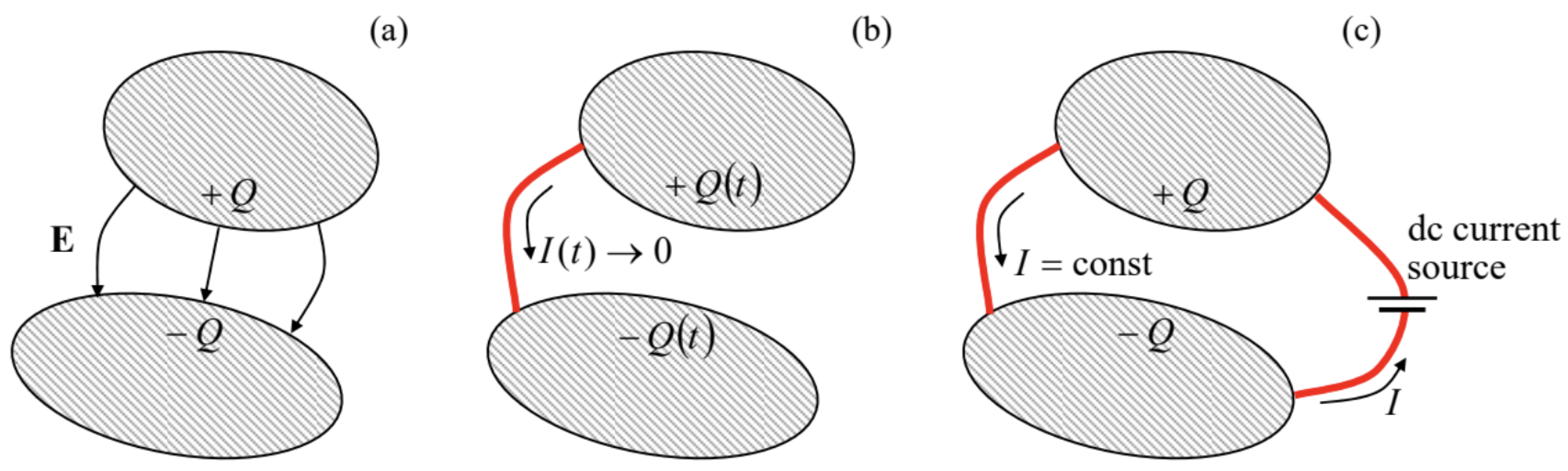
Ahora conectemos los dos conductores con un cable, un conductor delgado y alargado (Fig. 1b). Entonces el campo eléctrico provoca el movimiento de los portadores de carga en el cable, desde el conductor con un mayor potencial electrostático hacia el con menor potencial, hasta que los potenciales se equilibran. Tal proceso se llama relajación de carga. La ecuación principal que rige este proceso puede obtenerse del hecho experimental fundamental (ya mencionado en la Sec. 1.1) de que las cargas eléctricas no pueden aparecer o desaparecer, aunque las cargas opuestas pueden recombinarse con la conservación de la carga neta. Como resultado, la carga\(\ Q\) en un conductor puede cambiar solo debido a la corriente eléctrica\(\ I\) a través del cable:
\[\ \frac{d Q}{d t}=-I(t),\tag{4.1}\]
la relación que pueda entenderse como la definición de la corriente. 1
Expresemos la ecuación (1) en forma diferencial, introduciendo la noción de densidad de corriente\(\ \mathbf{j}(\mathbf{r})\). Este vector puede definirse a través de la siguiente relación para la corriente elemental que\(\ dI\) cruza un área elemental\(\ dA\) (Fig. 2):
\[\ d I=j d A \cos \theta=(j \cos \theta) d A=j_{n} d A,\tag{4.2}\]
donde\(\ \theta\) es el ángulo entre la dirección normal a la superficie y la dirección de movimiento del portador, que se toma para la dirección del vector\(\ \mathbf{j}\).
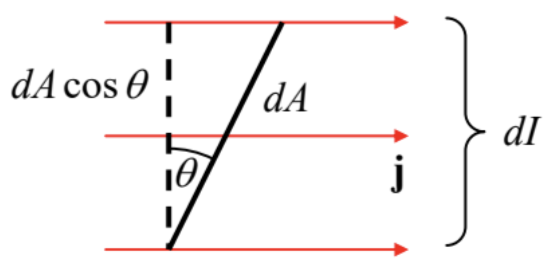Fig. 4.2. El vector de densidad de corriente j.Con esa definición, la ecuación (1) puede reescribirse como
\[\ \frac{d}{d t} \int_{V} \rho d^{3} r=-\oint_{S} j_{n} d^{2} r,\tag{4.3}\]
donde\(\ V\) es un volumen estacionario arbitrario limitado por la superficie cerrada\(\ S\). Aplicando a este volumen el mismo teorema de divergencia que se utilizó repetidamente en capítulos anteriores, obtenemos
\[\ \int_{V}\left[\frac{\partial \rho}{\partial t}+\nabla \cdot \mathbf{j}\right] d^{3} r=0.\tag{4.4}\]
Dado que el volumen\(\ V\) es arbitrario, esta ecuación puede ser cierta solo si
\[\ \frac{\partial \rho}{\partial t}+\nabla \cdot \mathbf{j}=0.\quad\quad\quad\quad\text{Continuity equation}\tag{4.5}\]
Esta es la ecuación fundamental de continuidad —que es cierta incluso para fenómenos dependientes del tiempo. 2
La relajación de carga, ilustrada por la Fig. 1b, es por supuesto un proceso dinámico dependiente del tiempo. Sin embargo, las corrientes eléctricas también pueden existir en situaciones estacionarias, cuando una cierta fuente de corriente, por ejemplo una batería, impulsa la corriente contra el campo eléctrico, y así repone las cargas del conductor y sostiene corrientes en un cierto nivel de tiempo independiente — ver Fig. 1c. (Este proceso requiere una reposición persistente de la energía electrostática del sistema, ya sea de una fuente o de un gran almacenamiento de energía de otro tipo, digamos, la energía química de la batería). Discutamos las leyes que rigen la distribución de tales corrientes de corriente continua. En este caso\(\ (\partial / \partial t=0)\), la ecuación (5) reduce a una ecuación muy simple
\[\ \nabla \cdot \mathbf{j}=0.\tag{4.6}\]
Esta relación adquiere una forma aún más simple en el caso particular pero importante de los circuitos eléctricos de CC (Fig. 3), los sistemas que pueden representarse de manera justa como conexiones directas (“galvánicas”) de componentes de dos tipos:
(i) elementos de circuito de pequeño tamaño (agrupados), es decir, una resistencia pasiva, una fuente de corriente, etc., generalmente, cualquier “caja negra” con dos o más terminales, y
(ii) cables perfectamente conductores, con una caída insignificante del potencial electrostático a lo largo de ellos, que están conectados galvánicamente en ciertos puntos llamados nodos (o “uniones”).
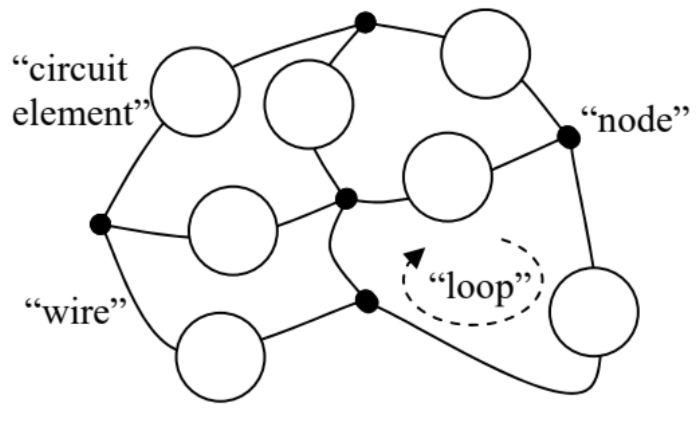Fig. 4.3. Un sistema típico que obedece las leyes de Kirchhoff.En la teoría de circuitos estándar, las cargas eléctricas de los nodos se consideran insignificantes, 3 y podemos integrar la ecuación (6) sobre la superficie cerrada dibujada alrededor de cualquier nodo para obtener una igualdad simple
\[\ \sum_{j} I_{j}=0,\tag{4.7a}\]
donde la suma está sobre todos los cables (numerados con índice\(\ j\)) conectados en el nodo. Por otro lado, según su definición (2.25), el voltaje a\(\ V_{k}\) través de cada elemento del circuito puede representarse como la diferencia de los potenciales electrostáticos de los nodos adyacentes,\(\ V_{k}=\phi_{k}-\phi_{k-1}\). Sumando tales diferencias alrededor de cualquier bucle cerrado del circuito (Fig. 3), obtenemos todos los términos cancelados, de manera que
\[\ \sum_{k} V_{k}=0.\tag{4.7b}\]
Estas relaciones se denominan, respectivamente, las leyes\(\ 1^{s t}\) y\(\ 2^{s t}\) Kirchhoff 4 —o a veces la regla de nodo (7a) y la regla de bucle (7b). Pueden parecer elementales, y su poder genuino está en el hecho matemático de que cualquier conjunto de ecuaciones. (7), cubriendo cada nodo y cada elemento de circuito del sistema al menos una vez, da un sistema de ecuaciones suficientes para el cálculo de todas las corrientes y voltajes en él —siempre que la relación entre el corriente y voltaje es conocido para cada elemento del circuito.
Es casi evidente que ante la ausencia de fuentes de corriente, el sistema de ecuaciones (7) solo tiene la solución trivial:\(\ I_{j}=0, V_{k}=0\) — con la exótica excepción de la superconductividad, a discutir en la Sec. 6.3. Las fuentes de corriente, que permiten flujos de corriente distintos de cero, pueden describirse por sus fuerzas electromotrices (e.m.f.) \(\ \mathscr{V}_{k}\), teniendo la dimensionalidad del voltaje, que hay que tomar en cuenta en los términos correspondientes\(\ V_{k}\) de la suma (7b). Permítanme esperar que el lector tenga alguna experiencia en el uso de las ecuaciones (7) para análisis de circuitos simples —digamos que constan de varias resistencias y baterías, para que pueda ahorrar tiempo omitiendo su discusión. Aún así, por su importancia práctica, recomendaría al lector realizar una autoprueba resolviendo un par de problemas ofrecidos al inicio de la Sec. 6.
Referencia
1 Así como un recordatorio (ojalá, :-) innecesario, en las unidades SI la corriente se mide en amperios (A). En metrología legal, el amperio (en lugar del culombo, que se define como 1C = 1A x 1s) es una unidad primaria. (Su definición formal se discutirá en el próximo capítulo.) En las unidades gaussianas, la ecuación (1) sigue siendo la misma, de manera que la unidad de la corriente es el statculomb por segundo —el llamado statampere.
2 Relaciones diferenciales similares son válidas para la densidad de cualquier cantidad conservada, por ejemplo para la masa en la dinámica de fluidos clásica (ver, e.g., CM Sec. 8.3), y para la probabilidad en física estadística (SM Sec. 5.6) y mecánica cuántica (QM Sec. 1.4).
3 En muchos casos, la acumulación/relajación de carga puede describirse sin una violación explícita de la Ec. (7a), simplemente agregando otros elementos del circuito, condensadores agrupados (ver Fig. 2.5 y su discusión), al circuito bajo análisis. El circuito resultante puede usarse para describir no solo los procesos transitorios sino también las corrientes de CA periódicas. No obstante, me conviene posponer la discusión de tales circuitos de CA hasta el Capítulo 6, donde se introducirá un tipo de elemento de circuito más, inductancias agrupadas.
4 Nombrado así por Gustav Kirchhoff (1824-1887) —quien también sugirió la forma diferencial (8) de la ley Ohm.