9.3:4 vectores, Momentum, Masa y Energía

Antes de proceder a la dinámica relativista, discutamos el formalismo matemático que hace que todos los cálculos sean más compactos —y más hermosos—. Ya hemos visto que las tres coordenadas espaciales\(\ \{x, y, z\}\) y el producto\(\ ct\) se transforman en Lorentz de manera similar — ver las ecuaciones (18) - (19) nuevamente. Por lo que es natural considerarlos como componentes de un solo vector de cuatro componentes (o, para abreviar, 4-vector),

\[\ \left\{x_{0}, x_{1}, x_{2}, x_{3}\right\} \equiv\{c t, \mathbf{r}\},\tag{9.48}\]

con componentes

\[\ x_{0} \equiv c t, \quad x_{1} \equiv x, \quad x_{2} \equiv y, \quad x_{3} \equiv z.\quad\quad\quad\quad\text{Space-time 4-vector}\tag{9.49}\]

Según las ecuaciones (19), sus componentes son transformados en Lorentz como

\[\ x_{j}=\sum_{j^{\prime}=0}^{3} L_{j j^{\prime}} x_{j^{\prime}}^{\prime},\quad\quad\quad\quad\text{Lorentz transform: 4-form}\tag{9.50}\]

donde\(\ L_{j j^{\prime}}\) están los elementos de la siguiente matriz de transformación de\(\ 4 \times 4\) Lorentz

\ [\\ izquierda (\ begin {array} {cccc}
\ gamma &\ beta\ gamma & 0 & 0\\ beta
\ gamma &\ gamma &\ gamma & 0 & 0\\
0 & 0 & 0 & 0 &
0 & 0 & 0 & 1
\ end {array}\ derecha). \ quad\ quad\ quad\ quad\ text {Matriz de transformación Lorentz}\ tag {9.51}\]

Dado que tales 4 vectores son una nueva noción para este curso y serán utilizados para muchos más propósitos que solo la transformación espacio-temporal, necesitamos discutir las reglas matemáticas generales que obedecen. En efecto, como ya se mencionó en la Sec. 8.9, el vector habitual (de tres componentes) no es cualquier conjunto ordenado (cadena) de tres escalares\(\ \left\{A_{x}, A_{y}, A_{z}\right\}\); si queremos que represente una realidad física independiente del marco de referencia, los componentes del vector tienen que obedecer ciertas reglas en la transferencia desde un marco de referencia a otro. En particular, en el límite no relativista la norma del vector (su magnitud al cuadrado),

\[\ A^{2}=A_{x}^{2}+A_{y}^{2}+A_{z}^{2},\tag{9.52}\]

debe ser invariante con respecto a la transferencia entre diferentes marcos de referencia. Sin embargo, una extensión ingenua de este enfoque a 4 vectores no funcionaría, ya que, según los cálculos de la Sec. 1, la transformada de Lorentz mantiene intactas las combinaciones del tipo (7), con un signo negativo, en lugar de la suma de todos los componentes al cuadrado. De ahí que para los 4 vectores, todas las reglas del juego tengan que ser revisadas y ajustadas —o más bien redefinidas desde el principio.

Un 4-vector arbitrario es una cadena de 4 escalares, ²³

\[\ \text{General 4-vector}\quad\quad\quad\quad \left\{A_{0}, A_{1}, A_{2}, A_{3}\right\},\tag{9.53}\]

cuyos componentes\(\ A_{j}\), medidos en los sistemas 0 y 0' mostrados en la Fig. 1, obedecen las relaciones de transformación de Lorentz similares a la Ec. (50):

\[\ \text{Lorentz transform: general 4-vector}\quad\quad\quad\quad A_{j}=\sum_{j^{\prime}=0}^{3} L_{j j^{\prime}} A_{j^{\prime}}^{\prime}.\tag{9.54}\]

Como ya hemos visto en el ejemplo del espacio-tiempo 4-vector (48), esto significa en particular que

\[\ \text{Lorentz invariance}\quad\quad\quad\quad A_{0}^{2}-\sum_{j=1}^{3} A_{j}^{2}=\left(A_{0}^{\prime}\right)^{2}-\sum_{j=1}^{3}\left(A_{j}^{\prime}\right)^{2}.\tag{9.55}\]

Esta es la llamada condición de invarianza de Lorentz para la norma de 4 vectores. (La diferencia entre esta relación y la Ec. (52), perteneciente a la geometría euclidiana, es la razón por la que el espacio Minkowski se llama pseudo-euclidiana.) También es sencillo utilizar las ecuaciones (51) y (54) para comprobar que una generalización evidente de la norma, el producto escalar de dos 4-vectores arbitrarios,

\[\ \text{Scalar 4-product}\quad\quad\quad\quad A_{0} B_{0}-\sum_{j=1}^{3} A_{j} B_{j},\tag{9.56}\]

también es invariante de Lorentz.

Ahora considere el vector 4 correspondiente a un pequeño intervalo entre dos eventos mundiales cercanos:

\[\ \left\{d x_{0}, d x_{1}, d x_{2}, d x_{3}\right\}=\{c d t, d \mathbf{r}\};\tag{9.57}\]

su norma,

\[\ \text{Interval}\quad\quad\quad\quad (d s)^{2} \equiv d x_{0}^{2}-\sum_{j=1}^{3} d x_{j}^{2}=c^{2}(d t)^{2}-(d r)^{2},\tag{9.58}\]

es, por supuesto, también Lorentz invariante. Dado que la velocidad de cualquier partícula (o señal) no puede ser mayor que\(\ c\), para cualquier par de eventos mundiales que estén en una relación causal entre sí,\(\ (d r)^{2}\) no puede ser mayor que\(\ (c d t)^{2}\), es decir, dicho intervalo similar al tiempo\(\ (d s)^{2}\) no puede ser negativo. La superficie 4D que separa dichos intervalos de los intervalos espaciales\(\ (d s)^{2}<0\) se llama cono de luz (Fig. 9).

Fig. 9.9. Una imagen dimensional 2+1 del cono de luz, que en realidad es 3+1 dimensional.

Ahora supongamos que dos eventos mundiales cercanos ocurren con la misma partícula que se mueve con velocidad u. Luego en el marco moviéndose con la partícula (v = u), en el lado derecho de la Ec. (58) el último término es igual a cero, mientras que el tiempo involucrado es el propio, de manera que

\[\ d s=c d \tau,\tag{9.59}\]

donde\(\ d \tau\) está el intervalo de tiempo adecuado. Pero según la ecuación (21), esto significa que podemos escribir

\[\ d \tau=\frac{d t}{\gamma},\tag{9.60}\]

donde\(\ dt\) es el intervalo de tiempo en un marco de referencia arbitrario (además de ser inercial), mientras que

\[\ \boldsymbol{\beta} \equiv \frac{\mathbf{u}}{c} \quad \text { and } \gamma \equiv \frac{1}{\left(1-\beta^{2}\right)^{1 / 2}}=\frac{1}{\left(1-u^{2} / c^{2}\right)^{1 / 2}}\tag{9.61}\]

son los parámetros (17) correspondientes a la velocidad de la partícula (\(\ \mathbf{u}\)) en ese marco, de manera que\(\ d s=c d t / \gamma\). ²⁴

Usemos la ecuación (60) para explorar si se puede formar un vector 4 usando los componentes espaciales de la velocidad de la partícula

\[\ \mathbf{u}=\left\{\frac{d x}{d t}, \frac{d y}{d t}, \frac{d z}{d t}\right\}.\tag{9.62}\]

Aquí tenemos un pequeño problema: como muestran las ecuaciones (22), estos componentes no obedecen a la transformación de Lorentz. Sin embargo, usemos\(\ d \tau \equiv d t / \gamma\), el intervalo de tiempo adecuado de la partícula, para formar la siguiente cadena:

\[\ \left\{\frac{d x_{0}}{d \tau}, \frac{d x_{1}}{d \tau}, \frac{d x_{2}}{d \tau}, \frac{d x_{3}}{d \tau}\right\} \equiv \gamma\left\{c, \frac{d x}{d t}, \frac{d y}{d t}, \frac{d z}{d t}\right\} \equiv \gamma\{c, \mathbf{u}\}.\quad\quad\quad\quad\text{4-velocity}\tag{9.63}\]

Como se desprende de la comparación de la forma media de esta expresión con la Ec. (48), dado que el vector tiempo-espacio obedece a la transformada de Lorentz, y\(\ \tau\) es Lorentz invariante, la cadena (63) es un 4-vector legítimo; se llama la velocidad 4 de la partícula.

Ahora estamos bien equipados para proceder a dinámicas relativistas. Empecemos con nociones tan básicas como el impulso\(\ \mathbf{p}\) y la energía\(\ \mathscr{E}\) -hasta ahora, para una partícula libre. ²⁵ Quizás la forma más elegante de “derivar” (o más bien adivinar ²⁶) las expresiones para\(\ \mathbf{p}\) y\(\ \mathscr{E}\) como funciones de la velocidad de la partícula\(\ \mathbf{u}\), se basa en la mecánica analítica. Debido a la conservación de\(\ \mathbf{v}\), la trayectoria de una partícula libre en el espacio 4D Minkowski\(\ \{c t, \mathbf{r}\}\) es siempre una línea recta. De ahí que, del principio Hamilton, ²⁷ podemos esperar que su acción\(\ \mathscr{S}\), entre los puntos 1 y 2, sea una función lineal del intervalo espacio-tiempo (59):

\[\ \text{Free particle: action}\quad\quad\quad\quad \mathscr{S}=\alpha \int_{1}^{2} d s \equiv \alpha c \int_{1}^{2} d \tau \equiv \alpha c \int_{t_{1}}^{t_{2}} \frac{d t}{\gamma},\tag{9.64}\]

donde\(\ \alpha\) hay alguna constante. Por otro lado, en la mecánica analítica, la acción se define como

\[\ \mathscr{S} \equiv \int_{t_{1}}^{t_{2}} \mathscr{L} d t,\tag{9.65}\]

donde\(\ \mathscr{L}\) está la función lagrangiana de la partícula. ²⁸ Comparando estas dos expresiones, obtenemos

\[\ \mathscr{L}=\frac{\alpha c}{\gamma} \equiv \alpha c\left(1-\frac{u^{2}}{c^{2}}\right)^{1 / 2}.\tag{9.66}\]

En el límite no relativista\(\ (u<<c)\), esta función tiende a

\[\ \mathscr{L} \approx \alpha c\left(1-\frac{u^{2}}{2 c^{2}}\right)=\alpha c-\frac{\alpha u^{2}}{2 c}.\tag{9.67}\]

Para corresponder a la mecánica newtoniana, ²⁹ el último término (dependiente de la velocidad) debe ser igual\(\ m u^{2} / 2\). De aquí nos encontramos\(\ \alpha=-m c\), para que, finalmente,

\[\ \text{Free particle: Lagrangian function}\quad\quad\quad\quad \mathscr{L}=-m c^{2}\left(1-\frac{u^{2}}{c^{2}}\right)^{1 / 2} \equiv-\frac{m c^{2}}{\gamma}.\tag{9.68}\]

Ahora podemos encontrar los componentes cartesianos\(\ p_{j}\) del momento de la partícula como el momento generalizado correspondiente a los componentes correspondientes\(\ r_{j}(j=1,2,3)\) del radio-vector 3D\(\ \mathbf{r}\): ³⁰

\[\ p_{j}=\frac{\partial \mathscr{L}}{\partial \dot{r}_{j}} \equiv \frac{\partial \mathscr{L}}{\partial u_{j}}=-m c^{2} \frac{\partial}{\partial u_{j}}\left(1-\frac{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}}{c^{2}}\right)^{1 / 2}=\frac{m u_{j}}{\left(1-u^{2} / c^{2}\right)^{1 / 2}} \equiv m \gamma u_{j}.\tag{9.69}\]

Así, para el vector 3D de momentum, podemos escribir el resultado en la misma forma que en la mecánica no relativista,

\[\ \mathbf{p}=m \gamma \mathbf{u} \equiv M \mathbf{u},\quad\quad\quad\quad \text{Relativistic momentum}\tag{9.70}\]

usando el escalar dependiente del marco de referencia\(\ M\) (llamado la masa relativista) definido como

\[\ M \equiv m \gamma=\frac{m}{\left(1-u^{2} / c^{2}\right)^{1 / 2}} \geq m,\quad\quad\quad\quad\text{Relativistic mass}\tag{9.71}\]

\(\ m\)siendo la masa no relativista de la partícula. (Más a menudo, m se llama la masa de reposo, porque en el marco de referencia en que descansa la partícula, la Eq. (71) rinde\(\ M = m\).)

A continuación, volvamos a la mecánica analítica para calcular la energía de la partícula\(\ \mathscr{E}\) (que para una partícula libre coincide con su función hamiltoniana\(\ \mathscr{H}\)): ³¹

\[\ \mathscr{E}=\mathscr{H}=\sum_{j=1}^{3} p_{j} u_{j}-\mathscr{L}=\mathbf{p} \cdot \mathbf{u}-\mathscr{L}=\frac{m u^{2}}{\left(1-u^{2} / c^{2}\right)^{1 / 2}}+m c^{2}\left(1-\frac{u^{2}}{c^{2}}\right)^{1 / 2} \equiv \frac{m c^{2}}{\left(1-u^{2} / c^{2}\right)^{1 / 2}}.\quad\quad\quad\quad \mathscr{E}=Mc^2\tag{9.73}\]

que expresa la relación entre la masa de la partícula libre y su energía. ³² En el límite no relativista, se reduce a

\[\ \mathscr{E}=\frac{m c^{2}}{\left(1-u^{2} / c^{2}\right)^{1 / 2}} \approx m c^{2}\left(1+\frac{u^{2}}{2 c^{2}}\right)=m c^{2}+\frac{m u^{2}}{2},\tag{9.74}\]

el primer término\(\ m c^{2}\) se llama la energía de reposo de una partícula.

Ahora consideremos la siguiente cadena de 4 escalares:

\[\ \left\{\frac{\boldsymbol{\mathscr{E}}}{\boldsymbol{c}}, p_{1}, p_{2}, p_{3}\right\} \equiv\left\{\frac{\boldsymbol{\mathscr{E}}}{\boldsymbol{c}}, \mathbf{p}\right\}.\quad\quad\quad\quad \text{4-vector of energy-momentum}\tag{9.75}\]

Usando las ecuaciones (70) y (73) para representar esta expresión como

\[\ \left\{\frac{\mathscr{E}}{c}, \mathbf{p}\right\}=m \gamma\{c, \mathbf{u}\},\tag{9.76}\]

y comparando el resultado con la Ec. (63), vemos inmediatamente que, dado que\(\ m\) es una constante invariante de Lorentz, esta cadena es un 4-vector legítimo de energía-impulso. En consecuencia, su norma,

\[\ \left(\frac{\mathscr{E}}{c}\right)^{2}-p^{2},\tag{9.77a}\]

es invariante de Lorentz, y en particular, tiene que ser igual a la norma en el marco unido a partículas. Pero en ese marco,\(\ p=0\), y, según la ecuación (73),\(\ \mathscr{E}=m c^{2}\), y para que la norma sea justa

\[\ \left(\frac{\mathscr{E}}{c}\right)^{2}=\left(\frac{m c^{2}}{c}\right)^{2} \equiv(m c)^{2},\tag{9.77b}\]

de manera que en un marco arbitrario

\[\ \left(\frac{\mathscr{E}}{c}\right)^{2}-p^{2}=(m c)^{2}.\tag{9.78a}\]

Esta relación tan importante ³³ entre la energía relativista y el impulso (¡válida solo para partículas libres!) generalmente se representa en la forma ³⁴

\[\ \text{Free particle: energy}\quad\quad\quad\quad \mathscr{E}^{2}=\left(m c^{2}\right)^{2}+(p c)^{2}.\tag{9.78b}\]

De acuerdo con la Ec. (70), en el llamado límite ultra-relativista\(\ u \rightarrow c\),\(\ p\) tiende al infinito, mientras que\(\ m c^{2}\) se mantiene constante para que eso\(\ p c / m c^{2} \rightarrow \infty\). Como se desprende de la Ec. (78), en este límite\(\ \mathscr{E} \approx p c\). Aunque la discusión anterior fue para partículas con finitas\(\ m\), el formalismo de 4 vectores permite considerar objetos compactos con masa de reposo cero como partículas ultra-relativistas para las cuales la relación energía-momento anterior,

\[\ \mathscr{E}=p c, \quad \text { for } m=0,\tag{9.79}\]

es exacto. La electrodinámica cuántica ³⁵ nos dice que bajo ciertas condiciones, los cuantos de campo electromagnético (fotones) también pueden considerarse como tales partículas sin masa con impulso\(\ \mathbf{p}=\hbar \mathbf{k}\). Conectando (el módulo de) la última relación en la Ec. (78), para la energía del fotón que obtenemos\(\ \mathscr{E}=p c=\hbar k c=\hbar \omega\). Tenga en cuenta nuevamente que según la Ec. (73), la masa relativista de un fotón no es igual a cero:\(\ M=\mathscr{E}/c^2=\hbar \omega / c^{2}\), de manera que el término “partícula sin masa” tiene un significado limitado:\(\ m = 0\). Por ejemplo, la masa relativista de un fonón óptico es del orden de\(\ 10^{-36} \mathrm{~kg}\). A escala humana, esto no es demasiado, sino que sigue siendo una parte notable (aproximadamente una millonésima) de la masa restante\(\ m_{\mathrm{e}}\) de un electrón.

Las relaciones fundamentales (70) y (73) se han verificado repetidamente en numerosos experimentos de colisión de partículas, en los que se conserva la energía total y el impulso de un sistema de partículas —en las mismas condiciones que en las dinámicas no relativistas—. (Para el impulso, esta es la ausencia de fuerzas externas, y para la energía, la elasticidad de las interacciones de las partículas, es decir, la ausencia de canales alternativos de escape de energía). Por supuesto, generalmente solo se conserva la energía total del sistema, incluyendo la energía potencial de las interacciones de partículas. Sin embargo, en colisiones típicas de partículas de alta energía, la energía potencial desaparece tan rápidamente con la distancia entre ellas que podemos
usar las leyes de impulso y conservación de energía usando la Ec. (73).

Como ejemplo, calculemos la energía mínima\(\ \mathscr{E}_{\mathrm{min}}\) de un protón\(\ \left(\mathrm{p}_{a}\right)\), necesaria para la conocida reacción de alta energía que genera un nuevo par protón-antiprotón\(\ \mathrm{p}_{a}+\mathrm{p}_{b} \rightarrow \mathrm{p}+\mathrm{p}+\mathrm{p}+\overline{\mathrm{p}}\), siempre que antes de la colisión, el protón\(\ \mathrm{p}_{b}\) hubiera estado en reposo en el marco de laboratorio. Este mínimo corresponde a la velocidad relativa de fuga de los productos de reacción, es decir, su movimiento con prácticamente la misma velocidad\(\ \left(\mathbf{u}_{\mathrm{fin}}\right)\), como se ve desde el marco del laboratorio — ver Fig. 10.

Fig. 9.10. Una reacción de protones de alta energía en\(\ \mathscr{E} \approx \mathscr{E}_{\min }\) - esquemáticamente.

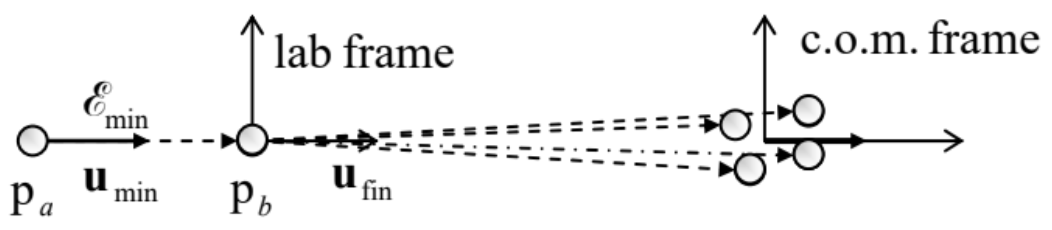
Debido a la conservación del momento, esta velocidad debe tener la misma dirección que la velocidad inicial\(\ \left(\mathbf{u}_{\min }\right)\) del protón\(\ p_{a}\). Es por ello que dos ecuaciones escalares: para la conservación de energía,

\[\ \frac{m c^{2}}{\left(1-u_{\min }^{2} / c^{2}\right)^{1 / 2}}+m c^{2}=\frac{4 m c^{2}}{\left(1-u_{\mathrm{fin}}^{2} / c^{2}\right)^{1 / 2}},\tag{9.80a}\]

y para la conservación del impulso,

\[\ \frac{m u}{\left(1-u_{\min }^{2} / c^{2}\right)^{1 / 2}}+0=\frac{4 m u_{\mathrm{fin}}}{\left(1-u_{\mathrm{fin}}^{2} / c^{2}\right)^{1 / 2}},\tag{9.80b}\]

son suficientes para encontrar ambos\(\ u_{\min }\) y\(\ u_{\mathrm{fin}}\). Después de una solución conceptualmente simple pero técnicamente algo tediosa de este sistema de dos ecuaciones no lineales, obtenemos

\[\ u_{\min }=\frac{4 \sqrt{3}}{7} c, \quad u_{\mathrm{fin}}=\frac{\sqrt{3}}{2} c.\tag{9.81}\]

Finalmente, podemos usar la Eq. (73) para calcular la energía requerida; el resultado es\(\ \mathscr{E}_{\min }=7 m c^{2}\). (Obsérvese que en este umbral, solo\(\ 2 m c^{2}\) de la energía cinética\(\ T_{\min }=\mathscr{E}_{\min }-m c^{2}=6 m c^{2}\) de la partícula móvil inicial, entra en la producción “útil” del par protón-antiprotón). La masa de reposo del protón,\(\ m_{\mathrm{p}} \approx 1.67 \times 10^{-27} \mathrm{~kg}\), corresponde a\(\ m_{\mathrm{p}} c^{2} \approx 1.502 \times 10^{-10} \mathrm{~J} \approx 0.938 \mathrm{GeV}\), así que\(\ \mathscr{E}_{\min } \approx 6.57 \mathrm{GeV}\).

La segunda forma, más inteligente, de resolver el mismo problema es utilizar el marco de referencia de centro de masa (c.o.m.) que, en relatividad, se define como el marco en que el impulso total del sistema se desvanece. ³⁶ En este marco, at\(\ \mathscr{E}=\mathscr{E}_{\min }\), la velocidad y momento de todos los productos de reacción están desapareciendo, mientras que las velocidades de los protones\(\ \mathrm{p}_{a}\) y\(\ \mathrm{p}_{b}\) antes de la colisión son iguales y opuestas, con una magnitud inicialmente desconocida\(\ u^{\prime}\). De ahí que la ley de conservación de energía se

\[\ \frac{2 m c^{2}}{\left(1-u^{\prime 2} / c^{2}\right)^{1 / 2}}=4 m c^{2},\tag{9.82}\]

dando fácilmente\(\ u^{\prime}=(\sqrt{3} / 2) c\). (Este es, por supuesto, el mismo resultado que la Ec. (81) da para\(\ u_{\text {fin }}\).) Ahora podemos usar el hecho de que la velocidad del protón\(\ \mathrm{p}_{a}\) en el cuadro c.o.m. es\(\ \left(-u^{\prime}\right)\), para encontrar su velocidad lab-frame, usando la transformada de velocidad (25):

\[\ u_{\min }=\frac{2 u^{\prime}}{1+u^{\prime 2} / c^{2}}.\tag{9.83}\]

Con el resultado anterior para\(\ u^{\prime}\), esta relación da el mismo resultado que el primer método,\(\ u_{\min }=(4 \sqrt{3} / 7) c\), pero de una manera más sencilla.

---

Referencia

²³ Se dice que tales vectores residen en los llamados espacios 4D Minkowski —llamados así por Hermann Minkowski quien fue el primero en refundir (en 1907) las relaciones especiales de relatividad en una forma en la que las coordenadas espaciales y el tiempo (o más bien ct) se tratan en pie de igualdad.

²⁴ He optado por usar índices especiales (e.g.,\(\ \boldsymbol{\beta}_{u}, \gamma_{u}\)) para distinguir las ecuaciones (17) y (61) aquí y abajo, con la esperanza de que la velocidad adecuada (ya sea de un marco de referencia o de una partícula) sea siempre clara desde el contexto.

²⁵ Siento haber usado, al igual que en la Sec. 6.3, la misma notación tradicional\(\ (\mathbf{p})\) para el impulso de la partícula que se había usado anteriormente para el momento dipolo eléctrico. No obstante, dado que esta última noción será prácticamente inutilizada en el balance de este curso, esto difícilmente puede llevar a confusión.

²⁶ En efecto, dicha derivación utiliza suposiciones adicionales, por naturales que sean (como la invarianza de Lorentz de\(\ \mathscr{S}\)), es decir, difícilmente puede considerarse como una prueba real de los resultados finales, por lo que requieren confirmación experimental. Afortunadamente, tales confirmaciones han sido numerosas — ver abajo.

²⁷ Véase, e.g., CM Sec. 10.3.

²⁸ Véase, e.g., CM Sec. 2.1.

²⁹ Véase, por ejemplo, CM Eq. (2.19b).

³⁰ Véase, por ejemplo, CM Sec. 2.3, en particular la Ec. (2.31).

³¹ Véase, por ejemplo, CM Eq. (2.32).

³² Permítanme esperar que el lector entienda que toda la charla laica sobre la “conversión de masa a energía” sólo es válida en un sentido muy limitado de la palabra. Si bien la relación de Einstein (73) sí permite la conversión de partículas “masivas” (con\(\ m \neq 0\)) en partículas con\(\ m=0\), como los fotones, cada una de estas últimas partículas también tiene una masa relativista distinta de cero\(\ M\), y simultáneamente la energía\(\ \mathscr{E}\) relacionada con esto\(\ M\) por la Eq. (73).

³³ Tenga en cuenta una relación más simple y útil que sigue de las Eq. (70) y (73):\(\ \mathbf{p}=\left(\mathscr{E} / c^{2}\right) \mathbf{u}\).

³⁴ Puede ser tentador interpretar esta relación como la adición en forma de vector perpendicular de la energía de reposo\(\ m c^{2}\) y la “energía cinética”\(\ pc\), pero desde el punto de vista de la conservación total de la energía (ver más adelante), una mejor definición de la energía cinética es\(\ T(u) \equiv \mathscr{E}(u)-\mathscr{E}(0)\).

³⁵ Se revisa brevemente en QM Capítulo 9.

³⁶ Obsérvese que de acuerdo con esta definición, el radio-vector del c.o.m. es\(\ \mathbf{R}=\Sigma_{k} M_{k} \mathbf{r}_{k} / \Sigma_{k} M_{k} \equiv \Sigma_{k} \gamma_{k} m_{k} \mathbf{r}_{k} / \Sigma_{k} \gamma_{k} m_{k}\), es decir, generalmente es diferente de la expresión no relativista bien conocida\(\ \mathbf{R}=\Sigma_{k} m_{k} \mathbf{r}_{k} / \Sigma_{k} m_{k}\).