5.6: Interferencia de onda: ondas estacionarias y latidos

Objetivos de aprendizaje

• Distinguir entre interferencia constructiva e interferencia destructiva.
• Explicar las ondas estacionarias en términos de interferencia, nodos y antinodos.
• Explicar el fenómeno beat en términos de interferencia.

Figura\(\PageIndex{1}\): Estas ondas son el resultado de la superposición de varias ondas de diferentes fuentes, produciendo un patrón complejo. (crédito: waterborough, Wikimedia Commons)

La mayoría de las olas no se ven muy simples. Se parecen más a las olas en Figura\(\PageIndex{1}\) que a la simple ola de agua considerada en “Olas”. (Las ondas simples pueden ser creadas por una simple oscilación armónica, y así tener una forma sinusoidal). Las olas complejas son más interesantes, incluso hermosas, pero se ven formidables. La mayoría de las ondas parecen complejas porque resultan de varias ondas simples que se suman. Por suerte, las reglas para sumar olas son bastante simples.

Cuando dos o más olas llegan al mismo punto, se superponen entre sí. Más específicamente, las perturbaciones de las olas se superponen cuando se unen, un fenómeno llamado superposición. Cada perturbación corresponde a una fuerza, y las fuerzas se suman. Si las perturbaciones están a lo largo de la misma línea, entonces la onda resultante es una simple adición de las perturbaciones de las ondas individuales, es decir, sus amplitudes suman. La figura\(\PageIndex{2}\) y la figura\(\PageIndex{3}\) ilustran la superposición en dos casos especiales, los cuales producen resultados simples.

La figura\(\PageIndex{2}\) muestra dos ondas idénticas que llegan al mismo punto exactamente en fase. Las crestas de las dos olas están alineadas con precisión, al igual que los canales. Esta superposición produce pura interferencia constructiva. Debido a que las perturbaciones se suman, la interferencia constructiva pura produce una onda que tiene el doble de amplitud de las ondas individuales, pero que tiene la misma longitud de onda.

La figura\(\PageIndex{3}\) muestra dos ondas idénticas que llegan exactamente fuera de fase, es decir, alineadas con precisión cresta a canal, produciendo pura interferencia destructiva. Debido a que las perturbaciones están en la dirección opuesta para esta superposición, la amplitud resultante es cero para la interferencia destructiva pura: las ondas se cancelan por completo.

Figura\(\PageIndex{2}\): La interferencia constructiva pura de dos ondas idénticas produce una con el doble de amplitud, pero la misma longitud de onda.

Figura\(\PageIndex{3}\): La interferencia destructiva pura de dos ondas idénticas produce amplitud cero, o cancelación completa.

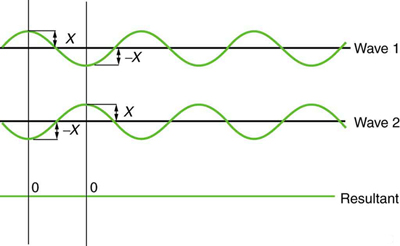
Si bien ocurren interferencias puramente constructivas y destructivas puras, requieren ondas idénticas alineadas con precisión. La superposición de la mayoría de las ondas produce una combinación de interferencia constructiva y destructiva y puede variar de un lugar a otro y de vez en cuando. El sonido de un estéreo, por ejemplo, puede ser fuerte en un lugar y silencioso en otro. Variable sonoridad significa que las ondas sonoras se agregan parcialmente constructivamente y parcialmente destructivamente en diferentes ubicaciones. Un estéreo tiene al menos dos altavoces que crean ondas sonoras, y las ondas pueden reflejarse desde las paredes. Todas estas ondas se superponen. Un ejemplo de sonidos que varían con el tiempo de constructivos a destructivos se encuentra en el gemido combinado de los jets de avión escuchados por un pasajero estacionario. El sonido combinado puede fluctuar hacia arriba y hacia abajo en volumen ya que el sonido de los dos motores varía en el tiempo de constructivo a destructivo. Estos ejemplos son de olas que son similares.

Un ejemplo de la superposición de dos ondas disímiles se muestra en la Figura\(\PageIndex{4}\). Aquí nuevamente, las perturbaciones suman y restan, produciendo una ola de mirada más complicada.

Figura\(\PageIndex{4}\): La superposición de ondas no idénticas presenta interferencia constructiva y destructiva.

Ondas Standing

A veces las olas no parecen moverse; más bien, simplemente vibran en su lugar. Se pueden ver olas inmóviles en la superficie de un vaso de leche en un refrigerador, por ejemplo. Las vibraciones del motor del refrigerador crean ondas en la leche que oscilan hacia arriba y hacia abajo pero no parecen moverse por la superficie. Estas ondas están formadas por la superposición de dos o más ondas móviles, tal como se ilustra en la Figura\(\PageIndex{5}\) para dos ondas idénticas que se mueven en direcciones opuestas. Las olas se mueven entre sí con sus perturbaciones sumando a medida que pasan. Si las dos ondas tienen la misma amplitud y longitud de onda, entonces alternan entre interferencia constructiva y destructiva. El resultante parece una ola de pie en su lugar y, así, se llama onda estacionaria. Las olas en el vaso de leche son un ejemplo de ondas estacionarias. Hay otras ondas estacionarias, como en cuerdas de guitarra y en pipas de órgano. Con el vaso de leche, las dos ondas que producen ondas estacionarias pueden provenir de reflejos del lado del vaso.

Una mirada más cercana a los terremotos proporciona evidencia de condiciones apropiadas para la resonancia, las ondas estacionarias y la interferencia constructiva y destructiva. Un edificio puede vibrar durante varios segundos con una frecuencia de manejo que coincide con la frecuencia natural de vibración del edificio, produciendo una resonancia que resulta en un edificio colapsando mientras que los edificios vecinos no lo hacen. A menudo los edificios de cierta altura están devastados mientras que otros edificios más altos permanecen intactos. La altura del edificio coincide con la condición para establecer una onda estacionaria para esa altura particular. A medida que las olas del terremoto viajan a lo largo de la superficie de la Tierra y se reflejan en rocas más densas, la interferencia constructiva ocurre en ciertos puntos. A menudo las zonas más cercanas al epicentro no se dañan mientras que las zonas más alejadas están dañadas.

Figura\(\PageIndex{5}\): Onda estacionaria creada por la superposición de dos ondas idénticas que se mueven en direcciones opuestas. Las oscilaciones se encuentran en ubicaciones fijas en el espacio y son el resultado de interferencias alternativamente constructivas y destructivas.

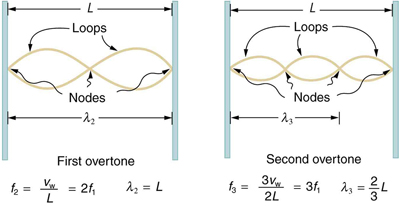
Las ondas estacionarias también se encuentran en las cuerdas de los instrumentos musicales y se deben a reflejos de ondas desde los extremos de la cuerda. La figura\(\PageIndex{6}\) y la figura\(\PageIndex{7}\) muestran tres ondas estacionarias que se pueden crear en una cuerda que se fija en ambos extremos. Los nodos son los puntos donde la cuerda no se mueve; más generalmente, los nodos son donde la perturbación de onda es cero en una onda estacionaria. Los extremos fijos de las cadenas deben ser nodos, también, porque la cadena no puede moverse allí. La palabra antinode se utiliza para denotar la ubicación de máxima amplitud en ondas estacionarias. Las ondas estacionarias en las cuerdas tienen una frecuencia que está relacionada con la velocidad\(v_{\mathrm{w}}\) de propagación de la perturbación en la cuerda. La longitud de onda\(\lambda\) está determinada por la distancia entre los puntos donde se fija la cadena en su lugar.

La frecuencia más baja, llamada frecuencia fundamental, es así para la longitud de onda más larga, que se ve que es\(\lambda_{1}=2 L\). Por lo tanto, la frecuencia fundamental es\(f_{1}=v_{\mathrm{w}} / \lambda_{1}=v_{\mathrm{w}} / 2 L\). En este caso, los armónicos o armónicos son múltiplos de la frecuencia fundamental. Como se ve en la Figura\(\PageIndex{7}\), el primer armónico se puede calcular fácilmente desde entonces\(\lambda_{2}=L\). Por lo tanto,\(f_{2}=v_{\mathrm{w}} / \lambda_{2}=v_{\mathrm{w}} / 2 L=2 f_{1}\). De igual manera\(f_{3}=3 f_{1}\),, y así sucesivamente. Todas estas frecuencias se pueden cambiar ajustando la tensión en la cuerda. Cuanto mayor es la tensión, mayor\(v_{\mathrm{w}}\) es y mayores son las frecuencias. Esta observación es familiar para cualquiera que alguna vez haya observado un instrumento de cuerda siendo afinado. Veremos en capítulos posteriores que las ondas estacionarias son cruciales para muchos fenómenos de resonancia, como en cajas de sondeo en instrumentos de cuerda.

Figura\(\PageIndex{6}\): La figura muestra una cuerda oscilando a su frecuencia fundamental.

Figura\(\PageIndex{7}\): Se muestran las frecuencias armónicas primera y segunda.

Beats

Colocar dos teclas adyacentes en un piano produce una combinación de urdimbre generalmente considerada desagradable. La superposición de dos ondas de frecuencias similares pero no idénticas es la culpable. Otro ejemplo a menudo se nota en los aviones a reacción, particularmente en la variedad de dos motores, mientras se realiza el rodaje. El sonido combinado de los motores sube y baja en volumen. Este volumen variable ocurre porque las ondas sonoras tienen frecuencias similares pero no idénticas. El gorjeo discordante del piano y la fluctuante sonoridad del ruido del motor a reacción se deben tanto a interferencias alternativamente constructivas como destructivas a medida que las dos ondas entran y salen de fase. La figura\(\PageIndex{8}\) ilustra esto gráficamente.

Figura\(\PageIndex{8}\): Los latidos son producidos por la superposición de dos ondas de frecuencias ligeramente diferentes pero amplitudes idénticas. Las ondas alternan en el tiempo entre la interferencia constructiva y la interferencia destructiva, dando a la onda resultante una amplitud variable en el tiempo.

La onda resultante de la superposición de dos ondas de frecuencia similar tiene una frecuencia que es el promedio de las dos. Esta onda fluctúa en amplitud, o latidos, con una frecuencia llamada frecuencia de latido. Podemos determinar la frecuencia de latidos sumando matemáticamente dos ondas juntas. El resultado,

\[f_{\mathrm{B}}=\left|f_{1}-f_{2}\right| \nonumber \]

es la frecuencia de latido. La onda resultante tiene la frecuencia promedio de las dos ondas superpuestas, pero también fluctúa en amplitud general a la frecuencia de latido\(f_{\mathrm{B}}\). Este resultado es válido para todo tipo de olas. No obstante, si se trata de una onda sonora, siempre que las dos frecuencias sean similares, entonces lo que escuchamos es una frecuencia promedio que se vuelve más fuerte y más suave (o warbles) a la frecuencia de latido.

Hacer conexiones profesionales

Los afinadores de piano utilizan ritmos de forma rutinaria en su trabajo. Al comparar una nota con un diapasón, escuchan ritmos y ajustan la cuerda hasta que los beats desaparezcan (a frecuencia cero). Por ejemplo, si el diapasón tiene una\(256 \mathrm{~Hz}\) frecuencia y se escuchan dos latidos por segundo, entonces la otra frecuencia es\(254\) o\(258 \mathrm{~Hz}\). La mayoría de las teclas golpean múltiples cadenas, y estas cuerdas en realidad se ajustan hasta que tienen casi la misma frecuencia y dan un ritmo lento para la riqueza. También se afinan guitarras y mandolinas de doce cuerdas usando beats.

Si bien los beats a veces pueden ser molestos en los sonidos audibles, encontraremos que los beats tienen muchas aplicaciones. Observar latidos es una forma muy útil de comparar frecuencias similares. Hay aplicaciones de latidos tan aparentemente dispares como en imágenes ultrasónicas y trampas de velocidad por radar.

Ejercicio\(\PageIndex{1}\)

Imagina que estás sosteniendo un extremo de una cuerda para saltar, y tu amigo sostiene el otro. Si tu amiga mantiene su extremo quieto, puedes mover tu extremo arriba y abajo, creando una onda transversal. Si tu amiga entonces comienza a mover su final arriba y abajo, generando una ola en sentido contrario, ¿qué formas de onda resultantes esperarías ver en la cuerda de saltar?

Contestar

La cuerda alternaría entre tener ondas con amplitudes dos veces la amplitud original y alcanzar el equilibrio sin amplitud en absoluto. Las longitudes de onda resultarán en interferencias tanto constructivas como destructivas.

Ejercicio\(\PageIndex{2}\)

Definir nodos y antinodos.

Contestar

Los nodos son áreas de interferencia de onda donde no hay movimiento. Los antinodos son áreas de interferencia de onda donde el movimiento está en su punto máximo.

Ejercicio\(\PageIndex{3}\)

Enganzas un sistema estéreo. Cuando pruebas el sistema, notas que en una esquina de la habitación, los sonidos parecen aburridos. En otra zona, los sonidos parecen excesivamente fuertes. Describir cómo el sonido que se mueve por la habitación podría resultar en estos efectos.

Contestar

Con múltiples altavoces apagando sonidos en la habitación, y estos sonidos rebotando en las paredes, seguramente habrá alguna interferencia de onda. En las zonas aburridas, la interferencia es probablemente en su mayoría destructiva. En las zonas más ruidosas, la interferencia es probablemente en su mayoría constructiva.

Resumen de la Sección

• La superposición es la combinación de dos olas en la misma ubicación.
• La interferencia constructiva ocurre cuando dos ondas se superponen en fase (ambas perturbaciones en la misma dirección).
• La interferencia destructiva ocurre cuando dos ondas se superponen exactamente fuera de fase (dos perturbaciones en direcciones opuestas).
• Una onda estacionaria es aquella en la que dos ondas se superponen para producir una onda que forma un patrón estacionario de nodos y antinodos, ubicaciones de no desplazamiento y de desplazamiento máximo.
• Las ondas estacionarias se forman a frecuencias de resonancia específicas, siendo la frecuencia más baja la frecuencia fundamental, y las frecuencias más altas se llaman armónicos o armónicos.
• Los latidos ocurren cuando ondas de frecuencias similares\(f_{1}\) y\(f_{2}\) se superponen. La amplitud resultante oscila con una frecuencia de latido dada por

  \[f_{\mathrm{B}}=\left|f_{1}-f_{2}\right|. \nonumber\]

Glosario

antinodo

la ubicación de la amplitud máxima en ondas estacionarias

frecuencia de latido

la frecuencia de las fluctuaciones de amplitud de una onda

interferencia constructiva

cuando dos olas llegan al mismo punto exactamente en fase; es decir, las crestas de las dos olas están alineadas con precisión, al igual que los canales

interferencia destructiva

cuando dos ondas idénticas llegan al mismo punto exactamente desfasadas; es decir, alineadas con precisión cresta a valle

frecuencia fundamental

la frecuencia más baja de una forma de onda periódica

nodos

los puntos donde la cuerda no se mueve; más generalmente, los nodos son donde la perturbación de la ola es cero en una onda estacionaria

armónicos

múltiplos de la frecuencia fundamental de un sonido

superposición

el fenómeno que ocurre cuando dos o más olas llegan al mismo punto