2.1: Masa

El cambio es imposible, afirmó el antiguo filósofo griego Parménides. Su trabajo no era científico, ya que no expuso sus ideas en una forma que les permitiera probarlas experimentalmente, pero la ciencia moderna, sin embargo, tiene un fuerte sabor parmenideo. Su argumento principal de que el cambio es una ilusión fue que algo no se puede convertir en nada, y de igual manera si no tienes nada, no puedes convertirlo en algo. Para convertir esto en una teoría científica, tenemos que decidir sobre una manera de medir lo que es “algo”, y luego podemos verificar mediante mediciones si la cantidad total de “algo” en el universo realmente se mantiene constante. ¿Cuánto “algo” hay en una roca? ¿Un rayo de sol cuenta como “algo”? ¿Cuenta el calor? ¿Movimiento? Pensamientos y sentimientos.

Si miras el índice de este libro, verás que los primeros cuatro capítulos tienen en ellos la palabra “conservación”. En física, una ley de conservación es una afirmación de que la cantidad total de una determinada cantidad física siempre permanece igual. Este capítulo trata sobre la conservación de la masa. El sistema métrico está diseñado alrededor de una unidad de distancia, el metro, una unidad de masa, el kilogramo y una unidad de tiempo, la segunda. La medición numérica de la distancia y el tiempo probablemente se remontan casi tan lejos en la prehistoria como contar dinero, pero la masa es un concepto más moderno. Hasta que los científicos se dieron cuenta de que la masa estaba conservada, no era obvio que pudiera haber una forma única y consistente de medir una cantidad de materia, de ahí jiggers de whisky y cordones de madera. Quizás te preguntes por qué no se descubrió la conservación de la masa hasta tiempos relativamente modernos, pero no era obvio, por ejemplo, que los gases tenían masa, y que la aparente pérdida de masa cuando se quemaba la madera estaba exactamente igualada por la masa de los gases que escapaban.

Una vez que los científicos estaban en el camino de la conservación del concepto de masa, comenzaron a buscar una manera de definir la masa en términos de un procedimiento de medición definido. Si intentaron tal procedimiento, y el resultado fue que llevó a la no conservación de la masa, entonces lo tirarían y probarían un procedimiento diferente. Por ejemplo, podríamos tener la tentación de definir la masa usando tazas medidores de cocina, es decir, como una medida de volumen. Entonces la masa estaría perfectamente conservada para un proceso como mezclar canicas con mantequilla de maní, pero habría procesos como congelar agua que condujeron a un aumento neto de masa, y otros como remojar agua con una esponja que provocara una disminución. Si, con el beneficio de la retrospectiva, parece que la definición de la taza medidora era simplemente tonta, entonces aquí hay un ejemplo más sutil de una definición incorrecta de masa. Supongamos que lo definimos usando una báscula de baño, o un dispositivo más preciso como una báscula postal que funciona según el mismo principio de usar la gravedad para comprimir o torcer un resorte. El problema es que la gravedad no es igual de fuerte en toda la superficie de la tierra, así que por ejemplo habría no conservación de la masa cuando lleves un objeto hasta la cima de una montaña, donde la gravedad es un poco más débil.

Si bien algunas de las posibilidades obvias tienen problemas, sí resultan haber al menos dos enfoques para definir la masa que llevan a que sea una cantidad conservada, por lo que consideramos que estas definiciones son “correctas” en el sentido pragmático de que lo correcto es lo que es útil.

Una definición que funciona es usar balanzas, pero compensar la fuerza local de la gravedad. Este es el método que utilizan los científicos que realmente se especializan en mediciones ultraprecisas. Un kilogramo estándar, en forma de cilindro de platino-iridio, se guarda en un santuario especial en París. Se hacen copias que se equilibran contra el kilogramo estándar en gravedad parisina, y luego se transportan a laboratorios en otras partes del mundo, donde se comparan con otras masas en la gravedad local. La cantidad definida de esta manera se denomina masa gravitacional.

Figura b: Una medida de la masa gravitacional: la esfera tiene una masa gravitacional de cinco kilogramos.

Un segundo y completamente diferente enfoque es medir lo difícil que es cambiar el estado de movimiento de un objeto. Esto nos dice su masa inercial. Por ejemplo, estaría más dispuesto a interponerme en el camino de un caniche que se aproxima que en el camino de un tren de carga, porque mi cuerpo tendrá más dificultades para convencer al tren de carga para que se detenga. Se trata de una definición conceptual de estilo diccionario, pero en física necesitamos respaldar una definición conceptual con una definición operativa, que es aquella que detalla las operaciones requeridas para medir la cantidad que se define. Podemos operacionalizar nuestra definición de masa inercial lanzando un kilogramo estándar a un objeto a una velocidad de 1 m/s (un metro por segundo) y midiendo la velocidad del objeto de retroceso. Supongamos que queremos medir la masa de un bloque de cemento en particular. Ponemos el bloque en un vagón de juguete en la acera, y le tiramos un kilogramo estándar. Supongamos que el kilogramo estándar golpea el vagón, y luego cae directamente hacia la acera, habiendo perdido toda su velocidad, y el vagón y el bloque interior retroceden a una velocidad de 0.23 m/s. luego repetimos el experimento con el bloque reemplazado por varios números de kilogramos estándar, y encontramos que podemos reproducir la velocidad de retroceso de 0.23 m/s con cuatro kilogramos estándar en el vagón. Hemos determinado que la masa del bloque es de cuatro kilogramos. ¹ Aunque esta definición de masa inercial tiene una atractiva simplicidad conceptual, obviamente no es muy práctica, al menos en esta forma cruda. Sin embargo, este método de colisión se parece mucho a los métodos utilizados para medir las masas de partículas subatómicas, que, después de todo, ¡no se pueden poner en pequeñas escalas postales!

Figura c: Una medida de la masa inercial: el vagón retrocede con la misma velocidad en los experimentos 1 y 2, estableciendo que la masa inercial del bloque de cemento es de cuatro kilogramos.

Los astronautas que pasan largos períodos de tiempo en el espacio necesitan monitorear su pérdida de masa ósea y muscular, y aquí también, es imposible medir la masa gravitacional. Como no quieren que se les arroje kilogramos estándar, utilizan una técnica ligeramente diferente (figuras d y e). Se atan a una silla que está unida a un resorte grande, y miden el tiempo que lleva un ciclo de vibración.

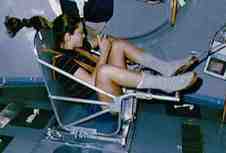
Figura d (izquierda): El tiempo de un ciclo de vibración está relacionado con la masa inercial del objeto.

Figura e (derecha): La astronauta Tamara Jernigan mide su masa inercial a bordo del transbordador espacial.

1.1.1 Técnicas de resolución de problemas

¿Cómo utilizamos una ley de conservación, como la conservación de masas, para resolver problemas? Hay dos técnicas básicas.

Como analogía, considere la conservación del dinero, lo que hace que sea ilegal que cree billetes de dólar usando su propia impresora de inyección de tinta. (¡La mayoría de la gente tampoco destruye intencionalmente sus billetes de dólar!) Supongamos que la policía nota que una tienda en particular no parece tener ningún cliente, pero el dueño usa muchas joyas de oro y conduce un BMW. Sospechan que la tienda es un frente para algún tipo de delito, quizá de falsificación. Con una vigilancia intensiva, existen dos enfoques básicos que podrían utilizar en su investigación. Un método sería que los agentes encubiertos traten de averiguar cuánto dinero entra por la puerta, y cuánto dinero vuelve a salir al final del día, tal vez arreglando a través de algún truco para tener acceso al maletín del dueño por la mañana y por la noche. Si la cantidad de dinero que sale todos los días es mayor que la cantidad que ingresó, y si están convencidos de que no hay caja fuerte en las instalaciones con un gran reservorio de dinero, entonces el dueño debe estar falsificando. Esta técnica de entrada-igual-salida es útil si estamos seguros de que existe una región de espacio dentro de la cual no hay suministro de masa que se esté construyendo o agotando.

Ejemplo 1: Una corriente de agua

Si observa que el agua fluye por el extremo de una manguera, verá que el chorro de agua es más gordo cerca de la boca de la manguera, y más flaco más abajo. Esto se debe a que el agua se acelera a medida que cae. Si el área de la sección transversal de la corriente fuera igual a lo largo de su longitud, entonces la velocidad de flujo (kilogramos por segundo) a través de una sección transversal inferior sería mayor que la velocidad de flujo a través de una sección transversal más alta hacia arriba. Dado que el flujo es constante, la cantidad de agua entre las dos secciones transversales se mantiene constante. Por lo tanto, la conservación de la masa requiere que el área transversal de la corriente se contraigan en proporción inversa a la velocidad creciente del agua que cae. f/Ejemplo 1.

autocomprobación:

Supongamos que apuntas la manguera hacia arriba, para que el agua suba en vez de caer. ¿Qué sucede a medida que la velocidad se hace más pequeña? ¿Qué sucede cuando la velocidad se vuelve cero?

(respuesta en la parte posterior de la versión PDF del libro)

¿Cómo podemos aplicar una ley de conservación, como la conservación de la masa, en una situación en la que la masa pueda almacenarse en algún lugar? Para volver a utilizar una analogía delictiva, una prisión podría contener cierto número de presos, a los que no se les permite entrar o salir a voluntad. En física, esto se conoce como un sistema cerrado. Un guardia podría notar que la celda de cierto preso está vacía, pero eso no significa que haya escapado. Podría estar enfermo en la enfermería, o trabajar duro en la tienda ganando dinero para fumar cigarrillos. Lo que realmente hacen las cárceles es contar todos los días a todos sus presos, y asegurarse de que el total de hoy sea el mismo que el de ayer. Una forma de afirmar una ley de conservación es que para un sistema cerrado, la cantidad total de cosas (masa, en este capítulo) se mantenga constante.

Ejemplo 2: Lavoisier y reacciones químicas en un sistema cerrado

El químico francés Antoine-Laurent Lavoisier es considerado el inventor del concepto de conservación de la masa. Antes de Lavoisier, los químicos nunca habían pesado sistemáticamente sus químicos para cuantificar la cantidad de cada sustancia que estaba experimentando reacciones. Tampoco entendieron completamente que los gases no eran más que otro estado de la materia, y no habían intentado realizar reacciones en cámaras selladas para determinar si los gases se estaban consumiendo o liberando al aire. Para ello tuvieron al menos una excusa práctica, que es que si realizas una reacción de liberación de gas en una cámara sellada sin espacio para la expansión, ¡obtienes una explosión! Lavoisier inventó una balanza que era capaz de medir masas de miligramos, y descubrió cómo hacer reacciones en un recipiente al revés en una cuenca de agua, para que los gases pudieran expandirse empujando parte del agua. En un experimento crucial, Lavoisier calentó un compuesto de mercurio rojo, que ahora describiríamos como óxido de mercurio (HGo), en una cámara sellada de este tipo. Se produjo un gas (Lavoisier más tarde lo llamó “oxígeno”), expulsando parte del agua, y el compuesto rojo se transformó en mercurio metálico líquido plateado. El punto crucial fue que la masa total de todo el aparato era exactamente la misma antes y después de la reacción. A partir de muchas observaciones de este tipo, Lavoisier propuso una ley general de la naturaleza, esa masa siempre se conserva. (¡En experimentos anteriores, en los que no se usaban sistemas cerrados, los químicos se habían convencido de que había una sustancia misteriosa, el flogistón, involucrada en las reacciones de combustión y oxidación, y que la masa del flogiston podría ser positiva, negativa o cero dependiendo de la situación!) a/Retrato de Monsieur Lavoisier y su esposa, de Jacques-Louis David, 1788. Lavoisier inventó el concepto de conservación de la masa. El esposo es representado con su aparato científico, mientras que en el fondo a la izquierda se encuentra el portafolio perteneciente a Madame Lavoisier, quien se cree que fue alumna de David's.

1.1.2 Notación delta

Una notación conveniente utilizada a lo largo de la física es\(\Delta\), la letra griega mayúscula delta, que indica “cambio en” o “después de menos antes”. Por ejemplo, si\(b\) representa cuánto dinero tienes en el banco, entonces un depósito de $100 podría representarse como $\ Delta {} b=$100$. Es decir, el cambio en su saldo fue de $100, o el saldo después de la transacción menos el saldo anterior a la transacción equivale a $100. Un retiro sería indicado por\(\Delta{}b\lt0\). Representamos “antes” y “después” usando los subíndices\(i\) (inicial) y\(f\) (final), e.g\(\Delta{}b=b_f-b_i\). A menudo la notación delta permite más precisión que las palabras inglesas. Por ejemplo, “tiempo” puede usarse para significar un punto en el tiempo (“ahora es el momento”)\(t\),, o podría significar un período de tiempo (“todo el tiempo, había escupido en la barbilla”),\(\Delta{}t\).

Esta notación es particularmente conveniente para discutir cantidades conservadas. La ley de conservación de la masa se puede afirmar simplemente como\(\Delta{}m=0\), donde\(m\) está la masa total de cualquier sistema cerrado.

autocomprobación:

Si\(x\) representa la ubicación de un objeto que se mueve en una dimensión, entonces ¿cómo\(\Delta{}x\) se interpretarían los signos positivos y negativos de?

(respuesta en la parte posterior de la versión PDF del libro)

Preguntas de Discusión

If an object had a straight-line \(x-t\) graph with \(\Delta x=0\) and \(\Delta t\ne0\), what would be true about its velocity? What would this look like on a graph? What about \(\Delta t=0\) and \(\Delta x\ne0\)?

Contributors and Attributions

Template:ContribCrowell