11.5: Circuitos LRC

El largo camino que iba desde la bombilla hasta la computadora comenzó con un paso muy importante: la introducción de la retroalimentación en los circuitos electrónicos. Si bien el principio de retroalimentación se ha entendido y aplicado a los sistemas mecánicos durante siglos, y a los eléctricos desde principios del siglo XX, para la mayoría de nosotros la palabra evoca una imagen de Jimi Hendrix (o algún héroe de la guitarra más reciente) creando intencionalmente chillidos desgarradores, o de los director de escuela haciendo lo mismo inadvertidamente en el auditorio. En el ejemplo de guitarra, el músico se para frente al amplificador y lo sube tan alto que las ondas sonoras que vienen del altavoz vuelven a la cuerda de la guitarra y la hacen temblar más fuerte. Este es un ejemplo de retroalimentación positiva: cuanto más fuerte vibra la cuerda, más fuertes son las ondas sonoras y cuanto más fuertes son las ondas sonoras, más fuerte vibra la cuerda. El único límite es la capacidad de manejo de potencia del amplificador.

La retroalimentación negativa es igualmente importante. Su termostato, por ejemplo, proporciona retroalimentación negativa al apagar el calentador cuando la casa se calienta lo suficiente, y al encenderlo nuevamente cuando hace demasiado frío. Esto hace que la temperatura de la casa oscile de un lado a otro dentro de un cierto rango. Así como los fenómenos exponenciales fuera de control son un comportamiento característico de los sistemas de retroalimentación positiva, la oscilación es típica en los casos de retroalimentación negativa. Ya has estudiado ampliamente la retroalimentación negativa en la sección 3.3 en el caso de un sistema mecánico, aunque no lo llamamos así.

Capacitancia e inductancia

En una oscilación mecánica, la energía se intercambia repetitivamente entre formas potenciales y cinéticas, y también puede ser desviada en forma de calor disipado por fricción. En un circuito eléctrico, las resistencias son los elementos del circuito que disipan el calor. ¿Cuáles son los análogos eléctricos de almacenar y liberar el potencial y la energía cinética de un objeto vibrante? Cuando piensas en el almacenamiento de energía en un circuito eléctrico, es probable que te imagines una batería, pero incluso las baterías recargables solo pueden pasar por 10 o 100 ciclos antes de que se desgasten. Además, las baterías no pueden intercambiar energía en una escala de tiempo lo suficientemente corta para la mayoría de las aplicaciones. El circuito en un sintetizador musical puede ser llamado a oscilar miles de veces por segundo, y su horno microondas opera a frecuencias de gigahercios. En lugar de baterías, generalmente usamos condensadores e inductores para almacenar energía en circuitos oscilantes. Los capacitores, que ya has encontrado, almacenan energía en campos eléctricos. Un inductor hace lo mismo con los campos magnéticos.

Capacitores

La energía de un condensador existe en sus campos eléctricos circundantes. Es proporcional al cuadrado de la intensidad de campo, que es proporcional a las cargas en las placas. Si asumimos que las placas llevan cargas que son las mismas en magnitud,\(+q\) y\(-q\), entonces la energía almacenada en el condensador debe ser proporcional a\(q^2\). Por razones históricas, escribimos la constante de proporcionalidad como\(1/2C\),

\[\begin{equation*} U_C = \frac{1}{2C}q^2 . \end{equation*}\]

La constante\(C\) es una propiedad geométrica del condensador, llamada su capacitancia.

a/El símbolo de un condensador.

b/Algunos capacitores.

Con base en esta definición, las unidades de capacitancia deben ser culombios cuadrados por julio, y esta combinación se abrevia más convenientemente como el farad,\(1\ \text{F}=1\ \text{C}^2/\text{J}\). “Condensador” es un término menos formal para un condensador. Tenga en cuenta que las etiquetas impresas en los capacitores a menudo usan MF para significar\(\mu\text{F}\), aunque MF realmente debería ser el símbolo de megafaradios, no microfaradios. La confusión no resulta de esta notación no estándar, ya que los valores de picofarad y microfaradios son los más comunes, y no fue hasta la década de 1990 que incluso los valores de milifaradios y faradios estuvieron disponibles en tamaños físicos prácticos. La figura a muestra el símbolo utilizado en los esquemas para representar un condensador.

Ejemplo\(\PageIndex{1}\): A parallel-plate capacitor

Supongamos que un condensador consta de dos placas metálicas paralelas con área\(A\), y el espacio entre ellas es\(h\). La brecha es pequeña en comparación con las dimensiones de las placas. ¿Cuál es la capacitancia?

Solución

Dado que las placas son metálicas, las cargas de cada placa son libres de moverse, y tenderán a agruparse más densamente cerca de los bordes debido a la repulsión mutua de las otras cargas en la misma placa. Sin embargo, resulta que si el hueco es pequeño, este es un efecto pequeño, por lo que podemos salirnos con la suya asumiendo una densidad de carga uniforme en cada placa. Entonces se aplica el resultado del ejemplo 14, y para la región entre las placas, tenemos

\[E=4\pi k\sigma=4\pi kq/ A\]

y

\[U_{e} = (1/8\pi k) E^2 Ah.\]

Sustituyendo la primera expresión por la segunda, encontramos\(U_{e}=2\pi kq^2 h/ A\). Comparando esto con la definición de capacitancia, terminamos con\(C= A/4\pi kh\).

Inductores

c/Dos geometrías comunes para inductores. La forma cilíndrica de la izquierda se llama solenoide.

Cualquier corriente creará un campo magnético, por lo que de hecho, ¡cada cable portador de corriente en un circuito actúa como inductor! Sin embargo, este tipo de inductancia “parásita” suele ser insignificante, así como generalmente podemos ignorar la resistencia parásita de nuestros cables y solo tomar en cuenta las resistencias reales. Para almacenar cualquier cantidad apreciable de energía magnética, generalmente se usa una bobina de alambre diseñada específicamente para ser un inductor. Todos los lazos de contribución al campo magnético se suman para hacer un campo más fuerte. A diferencia de los condensadores y resistencias, los inductores prácticos son fáciles de fabricar a mano. Por ejemplo, se puede enroscar un poco de alambre alrededor de un taco corto de madera. Un inductor como este, en forma de bobina cilíndrica de alambre, se llama solenoide, c, y un solenoide estilizado, d, es el símbolo utilizado para representar un inductor en un circuito independientemente de su geometría real.

d/El símbolo de un inductor.

e/Algunos inductores.

¿Cuánta energía almacena un inductor? La densidad de energía es proporcional al cuadrado de la intensidad del campo magnético, que a su vez es proporcional a la corriente que fluye a través del cable enrollado, por lo que la energía almacenada en el inductor debe ser proporcional a\(I^2\). Escribimos\(L/2\) para la constante de proporcionalidad, dando

\[\begin{equation*} U_L = \frac{L}{2}I^2 . \end{equation*}\]

Al igual que en la definición de capacitancia, tenemos un factor de 1/2, que es puramente una cuestión de definición. A la cantidad\(L\) se le llama inductancia del inductor, y vemos que sus unidades deben ser julios por amperio cuadrado. Esta torpe combinación de unidades se abrevia más comúnmente como henry, 1 henry = 1\(\text{J}/\text{A}^2\). En lugar de memorizar esta definición, tiene más sentido derivarla cuando sea necesario a partir de la definición de inductancia. Mucha gente conoce a los inductores simplemente como “bobinas” o “chokes”, y no te entenderán si te refieres a un “inductor”, pero aún así se referirán\(L\) como la “inductancia”, no la “coilance” o “¡estrangulamiento!”

Hay una aproximación de circuito agrupado para inductores, al igual que la de condensadores. Para un condensador, esto significa asumir que los campos eléctricos son completamente internos, de manera que los componentes solo interactúan a través de corrientes que fluyen a través de cables, no debido a la superposición física de sus campos en el espacio. De manera similar para un inductor, la aproximación del circuito agrupado es la suposición de que los campos magnéticos son completamente internos.

Ejemplo\(\PageIndex{2}\): Identical inductances in series

Si se colocan dos inductores en serie, cualquier corriente que pase a través del inductor doble combinado debe pasar por ambas partes. Si asumimos la aproximación del circuito agrupado, los campos de los dos inductores no interfieren entre sí, por lo que la energía se duplica para una corriente dada. Así, por la definición de inductancia, la inductancia también se duplica. En general, las inductancias en serie se suman, al igual que las resistencias. El mismo tipo de razonamiento también muestra que la inductancia de un solenoide es aproximadamente proporcional a su longitud, asumiendo que el número de vueltas por unidad de longitud se mantiene constante. (Esto es solo aproximadamente cierto, porque poner dos solenoides de extremo a extremo hace que los campos justo fuera de sus bocas se superpongan y se agreguen de manera complicada. En otras palabras, la aproximación del circuito de grumos puede no ser muy buena.)

f/Inductancias en serie add.

Ejemplo\(\PageIndex{3}\): Identical capacitances in parallel

Cuando dos capacitancias idénticas se colocan en paralelo, cualquier carga depositada en los terminales del condensador doble combinado se dividirá uniformemente entre las dos partes. Los campos eléctricos que rodean cada condensador serán la mitad de la intensidad, y por lo tanto almacenarán una cuarta parte de la energía. Dos capacitores, cada uno almacenando una cuarta parte de la energía, dan la mitad del almacenamiento total de energía. Dado que la capacitancia está inversamente relacionada con el almacenamiento de energía, esto implica que capacitancias idénticas en paralelo dan el doble de capacitancia. En general, se suman capacitancias en paralelo. Esto es diferente al comportamiento de inductores y resistencias, para lo cual las configuraciones en serie dan adición.

g/Capacitancias en paralelo agregar.

Esto es consistente con el resultado del ejemplo 18, que tenía la capacitancia de un solo condensador de placa paralela proporcional al área de las placas. Si tenemos dos condensadores de placa paralela, y los combinamos en paralelo y los acercamos muy juntos uno al lado del otro, hemos producido un solo condensador con placas de doble área, y tiene aproximadamente el doble de capacitancia, sujeto a cualquier violación de la aproximación del circuito grumoso debido a la interacción de los campos donde se unen los bordes de los capacitores.

Las inductancias en paralelo y las capacitancias en serie se exploran en los problemas de tareas 36 y 33.

Ejemplo\(\PageIndex{4}\): A variable capacitor

La Figura h/1 muestra la construcción de un condensador variable a partir de dos semicírculos paralelos de metal. Una placa es fija, mientras que la otra se puede girar alrededor de su eje común con una perilla. Las cargas opuestas en las dos placas son atraídas entre sí, y por lo tanto tienden a acumularse en el área de superposición. Esta área superpuesta, entonces, es la única área que efectivamente contribuye a la capacitancia, y al girar la perilla se cambia la capacitancia. El diseño simple solo puede proporcionar valores de capacitancia muy pequeños, por lo que en la práctica se suele utilizar un banco de condensadores, cableados en paralelo, con todas las partes móviles en un mismo eje.

h/Un condensador variable.

Preguntas de Discusión

◊ Supongamos que dos condensadores de placa paralela están cableados en paralelo, y se colocan muy juntos, uno al lado del otro, de modo que la aproximación del circuito agrupado no sea muy precisa. ¿La capacitancia resultante será demasiado pequeña o demasiado grande? ¿Podrías torcer el circuito en una forma diferente y hacer que el efecto sea al revés, o hacer que el efecto desaparezca? ¿Qué tal el caso de dos inductores en serie?

◊ La mayoría de los capacitores prácticos no tienen un espacio de aire o espacio de vacío entre las placas; en cambio, tienen una sustancia aislante llamada dieléctrico. Podemos pensar en las moléculas de esta sustancia como dipolos que son libres de rotar (al menos un poco), pero que no son libres para moverse, ya que es un sólido.

i/Pregunta de discusión B.

La figura muestra una forma muy estilizada y poco realista de visualizarla. Imaginamos que todos los dipolos son girados inicialmente de lado, (1), y que a medida que se carga el condensador, todos responden girando por cierto ángulo, (2). (En realidad, la escena podría ser mucho más aleatoria, y el efecto de alineación mucho más débil).

Para simplificar, imagina insertar solo un dipolo eléctrico en el hueco de vacío. Para una cantidad dada de carga en las placas, ¿cómo afecta esto a la cantidad de energía almacenada en el campo eléctrico? ¿Cómo afecta esto a la capacitancia?

Ahora rehacer el análisis en términos del trabajo mecánico necesario para cargar las placas.

10.5.2 Oscilaciones

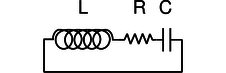
Circuito LRC serie j/A.

La figura j muestra el circuito oscilante más simple posible. Para cualquier aplicación útil en realidad necesitaría incluir más componentes. Por ejemplo, si se trataba de un sintonizador de radio, habría que conectarlo a una antena y a un amplificador. Sin embargo, toda la física esencial está ahí.

k/Una analogía mecánica para el circuito LRC.

Podemos analizarlo sin sudor ni lágrimas de ningún tipo, simplemente construyendo una analogía con un sistema mecánico. En un oscilador mecánico, k, tenemos dos formas de energía almacenada,

\[\begin{align*} U_{spring} &= \frac{1}{2}kx^2 &(1) \\ K &= \frac{1}{2}mv^2 . &(2) \end{align*}\]

En el caso de un oscilador mecánico, generalmente hemos asumido una fuerza de fricción de la forma que resulta dar los mejores resultados matemáticos,\(F=-bv\). En el circuito, la disipación de energía en calor se produce a través de la resistencia, sin fuerza mecánica involucrada, por lo que para hacer la analogía, necesitamos reafirmar el papel de la fuerza de fricción en términos de energía. La potencia disipada por la fricción equivale al trabajo mecánico que realiza en un intervalo de tiempo\(dt\), dividido por\(dt\),\(P=W/dt=Fdx/dt=Fv=-bv^2\), entonces

\[\begin{equation*} \text{rate of heat dissipation} = -bv^2 . (3) \end{equation*}\]

autocomprobación:

La ecuación (1) tiene\(x\) cuadrado, y las ecuaciones (2) y (3) han\(v\) cuadrado. Debido a que están al cuadrado, los resultados no dependen de si estas variables son positivas o negativas. ¿Esto tiene sentido físico? (respuesta en la parte posterior de la versión PDF del libro)

En el circuito, las formas de energía almacenadas son

\[\begin{align*} U_C &= \frac{1}{2C}q^2 &(1') \\ U_L &= \frac{1}{2}LI^2 , &(2') \end{align*}\]

y la tasa de disipación de calor en la resistencia es

\[\begin{equation*} \text{rate of heat dissipation} = -RI^2 . (3') \end{equation*}\]

Comparando los dos conjuntos de ecuaciones, primero formamos analogías entre cantidades que representan el estado del sistema en algún momento en el tiempo:

\[\begin{align*} x &\leftrightarrow q\\ v &\leftrightarrow I\\ \end{align*}\]

autocomprobación:

¿Cómo se\(v\) relaciona matemáticamente con\(x\)? ¿Cómo se\(I\) conecta a\(q\)? ¿Las dos relaciones son análogas? (respuesta en la parte posterior de la versión PDF del libro)

A continuación se relacionan las que describen las características permanentes del sistema:

\[\begin{align*} k &\leftrightarrow 1/C\\ m &\leftrightarrow L\\ b &\leftrightarrow R\\ \end{align*}\]

Dado que el sistema mecánico oscila naturalmente con una frecuencia ³\(\omega\approx\sqrt{k/m}\), podemos resolver inmediatamente la versión eléctrica por analogía, dando

\[\begin{equation*} \omega \approx \frac{1}{\sqrt{LC}} . \end{equation*}\]

Dado que la resistencia\(R\) es análoga a\(b\) en el caso mecánico, encontramos que el\(Q\) (factor de calidad, no carga) de la resonancia es inversamente proporcional a\(R\), y el ancho de la resonancia es directamente proporcional a\(R\).

Ejemplo 22: Sintonización de un receptor de radio

Un receptor de radio utiliza este tipo de circuito para seleccionar la estación deseada. Dado que el receptor resuena a una frecuencia particular, las estaciones cuyas frecuencias están muy alejadas no excitarán ninguna respuesta en el circuito. El valor de\(R\) tiene que ser lo suficientemente pequeño para que solo se recoja una estación a la vez, pero lo suficientemente grande como para que el sintonizador no sea demasiado delicada. La frecuencia resonante se puede ajustar ajustando cualquiera\(L\) o\(C\), pero los condensadores variables son más fáciles de construir que los inductores variables.

Ejemplo 23: Un cálculo numérico

La compañía telefónica envía más de una conversación a la vez por el mismo cable, lo que se logra cambiando cada señal de voz a diferentes rangos de frecuencias durante la transmisión. El número de señales por cable se puede maximizar haciendo que cada rango de frecuencias (conocido como ancho de banda) sea lo más pequeño posible. Resulta que solo es necesario un rango de frecuencias relativamente estrecho para que una voz humana sea inteligible, por lo que la compañía telefónica filtra todos los máximos y mínimos extremos. (Es por eso que la voz de tu teléfono suena diferente a tu voz normal). \(\triangleright\)Si el filtro consiste en un circuito LRC con una amplia resonancia centrada alrededor de 1.0 kHz, y el condensador es 1\(\mu\text{F}\) (microfaradios), ¿qué valor de inductancia se debe usar? \(\triangleright\)Resolviendo para\(L\), tenemos \[\begin{align*} L &= \frac{1}{ C\omega^2} \\ &= \frac{1}{(10^{-6}\ \text{F})(2\pi\times10^3\ \text{s}^{-1})^2} \\ &= 2.5\times10^{-3}\ \text{F}^{-1}\text{s}^2 \end{align*}\] Comprobando que estas realmente son las mismas unidades que henries es un poco tedioso, pero construye carácter: \[\begin{align*} \text{F}^{-1}\text{s}^2 &= (\text{C}^2/\text{J})^{-1}\text{s}^2 \\ &= \text{J}\cdot\text{C}^{-2}\text{s}^2 \\ &= \text{J}/\text{A}^2 \\ &= \text{H} \end{align*}\] El resultado es 25 mH (milihenrios). Esto es en realidad un valor de inductancia bastante grande, y requeriría una bobina grande, pesada y costosa. De hecho, hay un truco para hacer este tipo de circuito pequeño y barato. Existe una especie de chip de silicio llamado op-amp, que, entre otras cosas, se puede utilizar para simular el comportamiento de un inductor. La principal limitación del amplificador operacional es que está restringido a aplicaciones de baja potencia.

10.5.3 Voltaje y corriente

¿Qué sucede físicamente en uno de estos circuitos oscilantes? Primero veamos el caso mecánico, y luego dibujemos la analogía con el circuito. Por simplicidad, ignoremos la existencia de amortiguación, por lo que no hay fricción en el oscilador mecánico, ni resistencia en el eléctrico.

Supongamos que tomamos el oscilador mecánico y sacamos la masa del equilibrio, luego la liberamos. Dado que la fricción tiende a resistir la fuerza del resorte, podríamos esperar ingenuamente que tener cero fricción permitiría que la masa salte instantáneamente a la posición de equilibrio. Esto no puede suceder, sin embargo, porque la masa tendría que tener una velocidad infinita para poder dar un salto tan instantáneo. La velocidad infinita requeriría energía cinética infinita, pero el único tipo de energía que está disponible para la conversión a cinética es la energía almacenada en la primavera, y esa es finita, no infinita. En cada paso de su camino de regreso al equilibrio, la velocidad de la masa se controla exactamente por la cantidad de energía del resorte que hasta ahora se ha convertido en energía cinética. Después de que la masa alcanza el equilibrio, se rebasa debido a su propio impulso. Realiza oscilaciones idénticas en ambos lados del equilibrio, y nunca pierde amplitud porque la fricción no está disponible para convertir la energía mecánica en calor.

Ahora con el oscilador eléctrico, el análogo de posición es carga. Alejar la masa del equilibrio es como depositar cargas\(+q\) y\(-q\) en las placas del condensador. Dado que la resistencia tiende a resistir el flujo de carga, podríamos imaginar que sin fricción presente, la carga fluiría instantáneamente a través del inductor (que es, después de todo, solo un trozo de cable), y el condensador se descargaría instantáneamente. Sin embargo, tal descarga instantánea es imposible, porque requeriría una corriente infinita por un instante. La corriente infinita crearía campos magnéticos infinitos que rodeaban al inductor, y estos campos tendrían energía infinita. En cambio, la velocidad de flujo de corriente se controla en cada instante por la relación entre la cantidad de energía almacenada en el campo magnético y la cantidad de corriente que debe existir para tener ese campo fuerte. Después de que el condensador alcanza\(q=0\), se rebasa. El circuito tiene su propio tipo de “inercia” eléctrica, ya que si la carga dejara de fluir, tendría que haber cero corriente a través del inductor. Pero la corriente en el inductor debe estar relacionada con la cantidad de energía almacenada en sus campos magnéticos. Cuando el condensador está en\(q=0\), toda la energía del circuito está en el inductor, por lo que debe tener fuertes campos magnéticos rodeándolo y bastante corriente que lo atraviese.

Lo único que puede parecer espeluznante aquí es que solíamos hablar como si la corriente en el inductor causara el campo magnético, pero ahora suena como si el campo provocara la corriente. En realidad esto es sintomático de la escurridiza naturaleza de causa y efecto en la física. Es igualmente válido pensar en la relación de causa y efecto de cualquier manera. Esto puede parecer insatisfactorio, sin embargo, y por ejemplo realmente no llega a la pregunta de qué provoca una diferencia de voltaje a través de la resistencia (en el caso de que la resistencia sea finita); debe haber tal diferencia de voltaje, porque sin una, la ley de Ohm predeciría la corriente cero a través del resistencia.

El voltaje, entonces, es lo que realmente falta en nuestra historia hasta ahora.

Empecemos por estudiar el voltaje a través de un condensador. El voltaje es energía potencial eléctrica por unidad de carga, por lo que la diferencia de voltaje entre las dos placas del condensador está relacionada con la cantidad en la que su energía aumentaría si aumentáramos los valores absolutos de las cargas en las placas de\(q\) a\(q+dq\):

\[\begin{align*} V_C &= (U_{q+dq}-U_q)/dq \\ &= \frac{dU_C}{dq} \\ &= \frac{d}{dq}\left(\frac{1}{2C}q^2\right) \\ &= \frac{q}{C} \end{align*}\]

Muchos libros utilizan esto como la definición de capacitancia. Esta ecuación, por cierto, probablemente explica la razón histórica por la que\(C\) se definió de manera que la energía era inversamente proporcional a\(C\) para un valor dado de\(C\): las personas que inventaron la definición estaban pensando en un condensador como un dispositivo para almacenar carga en lugar de energía, y la cantidad de carga almacenada para un voltaje fijo (la “capacidad” de carga) es proporcional a\(C\).

l/El inductor libera energía y la da a la caja negra.

En el caso de un inductor, sabemos que si hay una corriente constante y constante que fluye a través de él, entonces el campo magnético es constante, y también lo es la cantidad de energía almacenada; no se está intercambiando energía entre el inductor y cualquier otro elemento del circuito. Pero, ¿y si la corriente está cambiando? El campo magnético es proporcional a la corriente, por lo que un cambio en uno implica un cambio en el otro. Para concretar, imaginemos que tanto el campo magnético como la corriente están disminuyendo. Por lo tanto, la energía almacenada en el campo magnético está disminuyendo, y por conservación de energía, esta energía no puede simplemente desaparecer; algún otro elemento del circuito debe estar tomando energía del inductor. El ejemplo más simple, mostrado en la figura l, es un circuito en serie que consiste en el inductor más otro elemento del circuito. No importa cuál sea este otro elemento del circuito, así que solo lo llamamos caja negra, pero si quieres, podemos pensarlo como una resistencia, en cuyo caso la energía perdida por el inductor está siendo convertida en calor por la resistencia. La regla de unión nos dice que ambos elementos del circuito tienen la misma corriente a través de ellos, por lo que\(I\) podría referirse a cualquiera de ellos, y de igual manera la regla de bucle nos dice\(V_{inductor}+V_{black\ box}=0\), por lo que las dos caídas de voltaje tienen el mismo valor absoluto, al que podemos referirnos como\(V\). Cualquiera que sea la caja negra, la velocidad a la que está tomando energía del inductor viene dada por\(|P|=|IV|\), entonces

\[\begin{align*} |IV| &= \left|\frac{dU_L}{dt}\right| \\ &= \left|\frac{d}{dt}\left( \frac{1}{2}LI^2\right) \right| \\ &= \left|LI\frac{dI}{dt}\right| ,\\ \text{or} |V| &= \left|L\frac{dI}{dt}\right| , \\ \end{align*}\]

que en muchos libros se toma como la definición de inductancia. La dirección de la caída de voltaje (signo más o menos) es tal que el inductor resiste el cambio de corriente.

Hay una cosa muy intrigante sobre este resultado. Supongamos, para concreción, que la caja negra de la figura l es una resistencia, y que la energía del inductor está disminuyendo, y siendo convertida en calor en la resistencia. La caída de voltaje a través de la resistencia indica que tiene un campo eléctrico a través de ella, que está impulsando la corriente. Pero, ¿de dónde viene este campo eléctrico? ¡No hay cargos en ningún lado que puedan estar creándolo! Lo que hemos descubierto es un caso especial de un principio más general, el principio de inducción: un campo magnético cambiante crea un campo eléctrico, que se suma a cualquier campo eléctrico creado por cargas. (Lo contrario también es cierto: cualquier campo eléctrico que cambie con el tiempo crea un campo magnético). La inducción forma la base de tecnologías como el generador y el transformador, y en última instancia conduce a la existencia de la luz, que es un patrón de onda en los campos eléctrico y magnético. Todos estos son temas para el capítulo 11, pero es verdaderamente notable que pudiéramos llegar a esta conclusión sin haber aprendido todavía ningún detalle sobre el magnetismo.

m/Campos eléctricos hechos por cargas, 1, y cambiando campos magnéticos, 2 y 3.

Los dibujos animados en la figura m comparan los campos eléctricos hechos por cargas, 1, con campos eléctricos hechos cambiando los campos magnéticos, 2-3. En m /1, dos físicos se encuentran en una habitación cuyo techo está cargado positivamente y cuyo piso está cargado negativamente. El físico en el fondo lanza una bola de boliche cargada positivamente en la tubería curva. El físico en la parte superior utiliza una pistola de radar para medir la velocidad de la pelota a medida que sale de la tubería. Encuentran que la pelota se ha ralentizado para cuando llega a la cima. Al medir el cambio en la energía cinética de la pelota, los dos físicos están actuando igual que un voltímetro. Concluyen que la parte superior del tubo está a un voltaje mayor que el fondo de la tubería. Una diferencia de voltaje indica un campo eléctrico, y este campo claramente está siendo causado por las cargas en el piso y el techo.

En m /2, no hay cargos en ninguna parte de la habitación excepto por la bola de boliche cargada. Las cargas móviles hacen campos magnéticos, por lo que hay un campo magnético que rodea la tubería helicoidal mientras la bola se mueve a través de ella. Se ha creado un campo magnético donde antes no había ninguno, y ese campo tiene energía. ¿De dónde podría haber salido la energía? Sólo puede haber venido de la bola misma, por lo que la pelota debe estar perdiendo energía cinética. Los dos físicos que trabajan juntos vuelven a actuar como voltímetro, y nuevamente concluyen que existe una diferencia de voltaje entre la parte superior e inferior de la tubería. Esto indica un campo eléctrico, pero este campo eléctrico no puede haber sido creado por ningún cargo, porque no hay ninguno en la habitación. Este campo eléctrico fue creado por el cambio en el campo magnético.

El físico de fondo sigue lanzando bolas a la tubería, hasta que la tubería está llena de bolas, m /3, y finalmente se establece una corriente constante. Mientras la tubería se llenaba de bolas, la energía en el campo magnético aumentaba constantemente, y esa energía estaba siendo robada de la energía cinética de las bolas. Pero una vez que se establece una corriente constante, la energía en el campo magnético ya no cambia. Las bolas ya no tienen que renunciar a la energía para construir el campo, y el físico en la parte superior encuentra que las bolas están saliendo de la tubería a toda velocidad nuevamente. Ya no hay diferencia de voltaje. A pesar de que hay una corriente,\(dI/dt\) es cero.

Ejemplo 24: Balastros

En un tubo de descarga de gas, como un letrero de neón, se aplica suficiente voltaje a un tubo lleno de gas para ionizar algunos de los átomos en el gas. Una vez que se han creado los iones, el voltaje los acelera, y golpean otros átomos, ionizándolos también y dando como resultado una reacción en cadena. Esto es una chispa, como un rayo. Pero una vez que arranca la chispa, el dispositivo comienza a actuar como si no tuviera resistencia: cada vez más flujos de corriente, sin necesidad de aplicar más voltaje. El poder,\(P=IV\), crecería sin límite, y el tubo se quemaría. n/Balastros para luces fluorescentes. Top: un inductor grande y pesado utilizado como balasto en una bombilla fluorescente anticuada. Fondo: un pequeño balasto de estado sólido, integrado en la base de una moderna bombilla fluorescente compacta. La solución más simple es conectar un inductor, conocido como el “balasto”, en serie con el tubo, y ejecutar todo con una tensión de CA. Durante cada ciclo, a medida que el voltaje alcanza el punto donde comienza la reacción en cadena, hay una oleada de corriente, pero el inductor resiste un cambio tan repentino de corriente, y la energía que de otro modo habría quemado la bombilla se canaliza en su lugar hacia la construcción de un campo magnético. Una bombilla fluorescente doméstica común consiste en un tubo de descarga de gas en el que el vidrio está recubierto con un material fluorescente. El gas en el tubo emite luz ultravioleta, que es absorbida por el recubrimiento, y el recubrimiento luego brilla en el espectro visible. Hasta hace poco, era común que un balasto de luz fluroescente fuera un inductor simple, y que todo el dispositivo funcionara a la frecuencia de 60 Hz de las líneas eléctricas. Esto provocó que las luces parpadearan molestamente a 120 Hz, y también podría provocar un zumbido audible, ya que el campo magnético que rodea al inductor podría ejercer fuerzas mecánicas sobre las cosas. En estos días, la tendencia es hacia el uso de un circuito de estado sólido que imita el comportamiento de un inductor, pero a una frecuencia en el rango de kilohercios, eliminando el parpadeo y el zumbido. Las modernas bombillas fluorescentes compactas electrónicas tienen balastos integrados en sus bases, por lo que pueden ser utilizadas como reemplazos enchufables para bombillas incandescentes. Una bombilla fluorescente compacta utiliza aproximadamente 1/4 de la electricidad de una bombilla incandescente, dura diez veces más y ahorra 30 dólares en electricidad a lo largo de su vida útil.

Pregunta de Discusión

◊ ¿Qué sucede cuando el físico en la parte inferior en la figura m /3 comienza a cansarse, y disminuye la corriente?

10.5.4 Decaimiento

Hasta ahora he pedaleado suave el hecho de que al cambiar las características de un oscilador, es posible producir un comportamiento no oscilatorio. Por ejemplo, imagínese tomar el sistema de masa sobre un resorte y hacer que el resorte sea cada vez más débil. En el límite de los pequeños\(k\), es como si no hubiera resorte alguno, y el comportamiento del sistema es que si pateas la masa, simplemente comienza a disminuir la velocidad. Para la fricción proporcional a\(v\), como venimos asumiendo, el resultado es que la velocidad se aproxima a cero, pero nunca llega a cero. Esto no es realista para el oscilador mecánico, que no tendrá fricción de fuga a bajas velocidades, pero es bastante realista en el caso de un circuito eléctrico, para lo cual la caída de voltaje a través de la resistencia realmente se acerca a cero a medida que la corriente se acerca a cero.

Ni siquiera tenemos que reducir exactamente\(k\) a cero para obtener un comportamiento no oscilatorio. En realidad hay un valor finito, crítico por debajo del cual cambia el comportamiento, de manera que la masa ni siquiera lo hace a través de un ciclo. Este es el caso del sobreamortiguamiento, discutido en la página 186.

Los circuitos eléctricos pueden exhibir el mismo comportamiento. Por simplicidad analizaremos solo los casos de circuitos LRC con\(L=0\) o\(C=0\).

El circuito RC

o/Un circuito RC.

Primero analizamos el circuito RC, o. En realidad uno tendría que “patear” el circuito, por ejemplo insertando brevemente una batería, para obtener algún comportamiento interesante. Comenzamos con la ley de Ohm y la ecuación para el voltaje a través de un condensador:

\[\begin{align*} V_R &= IR \\ V_C &= q/C \end{align*}\]

La regla del bucle nos dice

\[\begin{equation*} V_R + V_C = 0 , \end{equation*}\]

y combinar las tres ecuaciones da como resultado una relación entre\(q\) y\(I\):

\[\begin{equation*} I = -\frac{1}{RC}q \end{equation*}\]

El signo negativo nos dice que la corriente tiende a reducir la carga en el condensador, es decir, a descargarla. Tiene sentido que la corriente sea proporcional a\(q\): si\(q\) es grande, entonces las fuerzas de atracción entre las\(-q\) cargas\(+q\) y en las placas del condensador son grandes, y las cargas fluirán más rápidamente a través de la resistencia para reunirse. Si hubiera carga cero en las placas del condensador, no habría razón para que la corriente fluya. Dado que los amperios, la unidad de corriente, son los mismos que los culombios por segundo, parece que la cantidad\(RC\) debe tener unidades de segundos, y puedes comprobar por ti mismo que esto es correcto. \(RC\)por lo tanto, se conoce como la constante de tiempo del circuito.

¿Cómo exactamente\(I\) y\(q\) varían con el tiempo? Reescribiendo\(I\) como\(dq/dt\), tenemos

\[\begin{equation*} \frac{dq}{dt} = -\frac{1}{RC}q . \end{equation*}\]

Necesitamos una función\(q(t)\) cuya derivada se iguale a sí misma, pero multiplicada por una constante negativa. Una función de la forma\(ae^t\), donde\(e=2.718...\) está la base de logaritmos naturales, es la única que tiene su derivada igual a sí misma, y\(ae^{bt}\) tiene su derivada igual a sí misma multiplicada por\(b\). Así nuestra solución es

\[\begin{equation*} q = q_\text{o}\exp\left(-\frac{t}{RC}\right) . \end{equation*}\]

p/En un intervalo de tiempo\(RC\), la carga en el condensador se reduce en un factor de\(e\).

El circuito RL

q/Un circuito RL.

El circuito RL, q, puede ser atacado por métodos similares, y se puede demostrar fácilmente que da

\[\begin{equation*} I = I_\text{o}\exp\left(-\frac{R}{L}t\right) . \end{equation*}\]

La constante de tiempo RL es igual\(L/R\).

Ejemplo 25 Muerte por solenoide; bujías

Cuando de repente rompemos un circuito de RL, ¿qué pasará? Podría parecer que nos enfrentamos a una paradoja, ya que sólo tenemos dos formas de energía, la energía magnética y el calor, y si la corriente se detiene repentinamente, el campo magnético debe colapsar repentinamente. Pero, ¿a dónde va la energía magnética perdida? No puede entrar en calentamiento resistivo de la resistencia, porque el circuito ya se ha roto, ¡y la corriente no puede fluir! La salida de este acertijo es reconocer que la brecha abierta en el circuito tiene una resistencia que es grande, pero no infinita. Esta gran resistencia hace que la constante\(L/ R\) de tiempo RL sea muy pequeña. Por lo tanto, la corriente continúa fluyendo por un tiempo muy breve, y fluye directamente a través del entrehierro donde se ha abierto el circuito. En otras palabras, ¡hay una chispa! Podemos determinar con base en varias líneas de razonamiento diferentes que la caída de voltaje de un extremo de la chispa al otro debe ser muy grande. Primero, la resistencia del aire es grande, por lo que\(V= IR\) requiere un voltaje grande. También podemos razonar que toda la energía en el campo magnético se está disipando en poco tiempo, por lo que la potencia disipada en la chispa,\(P= IV\), es grande, y esto requiere un gran valor de\(V\). (\(I\)no es grande — está disminuyendo desde su valor inicial.) Sin embargo, una tercera forma de alcanzar el mismo resultado es considerar la ecuación\(V_{L}=dI/dt\): dado que la constante de tiempo es corta, la derivada de tiempo\(dI/dt\) es grande. Así es exactamente como funcionan las bujías de un automóvil. Otra aplicación es a la seguridad eléctrica: puede ser peligroso romper un circuito inductivo repentinamente, porque se libera tanta energía en poco tiempo. Tampoco hay garantía de que la chispa se descargue a través del espacio de aire; en su lugar podría pasar por tu cuerpo, ya que tu cuerpo podría tener una menor resistencia.

Ejemplo 26: Un transmisor de radio de chispa

r/Ejemplo 26. La figura r muestra un tipo primitivo de radiotransmisor, llamado transmisor de chispa, utilizado para enviar código Morse a principios del siglo XX. La fuente de alto voltaje, V, es típicamente de aproximadamente 10,000 voltios. Cuando el interruptor de telégrafo, S, está cerrado, el circuito RC de la izquierda comienza a cargarse. Se desarrolla una diferencia de voltaje creciente entre los electrodos de la brecha de chispa, G. Cuando esta diferencia de voltaje se vuelve lo suficientemente grande, el campo eléctrico en el aire entre los electrodos provoca una chispa, descargando parcialmente el circuito RC, pero cargando el circuito LC a la derecha. El circuito LC oscila entonces a su frecuencia resonante (típicamente alrededor de 1 MHz), pero la energía de estas oscilaciones es irradiada rápidamente por la antena, A, que envía ondas de radio (capítulo 11).

Preguntas de Discusión

◊ Una ardilla roe a través de uno de los cables del sistema de iluminación de CC en su patio delantero, y las luces se apagan. En el instante en que el circuito se abre, podemos considerar que los extremos desnudos del cable son como las placas de un condensador, con un entrehierro (o Gopher gap) entre ellas. ¿De qué tipo de valor de capacitancia estamos hablando aquí? ¿Qué te diría esto de la constante de\(RC\) tiempo?

10.5.5 Revisión de números complejos

s/Visualizar números complejos como puntos en un plano.

Para un tratamiento más detallado de los números complejos, consulte el capítulo 3 del libro gratuito de James Nearing en
http://www.physics.miami.edu/nearing/mathmethods/.

Suponemos que hay un número,\(i\), tal que\(i^2=-1\). Las raíces cuadradas de\(-1\) son entonces\(i\) y\(-i\). (En trabajos de ingeniería eléctrica, donde\(i\) significa corriente, a veces\(j\) se utiliza en su lugar.) Esto da lugar a un sistema numérico, llamado los números complejos, que contiene los números reales como subconjunto. Cualquier número complejo\(z\) puede escribirse en la forma\(z=a+bi\), donde\(a\) y\(b\) son reales,\(a\) y luego\(b\) se les conoce como las partes reales e imaginarias de\(z\). Un número con una parte real cero se llama número imaginario. Los números complejos se pueden visualizar como un plano, con la línea numérica real colocada horizontalmente como el\(x\) eje del\(x-y\) plano familiar, y los números imaginarios corriendo a lo largo del\(y\) eje. Los números complejos están completos de una manera que los números reales no lo son: cada número complejo distinto de cero tiene dos raíces cuadradas. Por ejemplo, 1 es un número real, por lo que también es miembro de los números complejos, y sus raíces cuadradas son\(-1\) y 1. De igual manera,\(-1\) tiene raíces cuadradas\(i\) y\(-i\), y el número\(i\) tiene raíces cuadradas\(1/\sqrt{2}+i/\sqrt{2}\) y\(-1/\sqrt{2}-i/\sqrt{2}\).

Los números complejos se pueden sumar y restar sumando o restando sus partes reales e imaginarias. Geométricamente, esto es lo mismo que la adición de vectores.

t/La suma de números complejos es igual que la suma de vectores, aunque los ejes real e imaginario no representan en realidad direcciones en el espacio.

Los números complejos\(a+bi\) y\(a-bi\), que se encuentran a distancias iguales por encima y por debajo del eje real, se denominan conjugados complejos. Los resultados de la fórmula cuadrática son conjugados tanto reales como complejos entre sí. El conjugado complejo de un número\(z\) se anota como\(\bar{z}\) o\(z^*\).

u/Un número complejo y su conjugado.

Los números complejos obedecen todas las mismas reglas aritméticas que los reales, excepto que no se pueden ordenar a lo largo de una sola línea. Es decir, no es posible decir si un número complejo es mayor que otro. Podemos compararlos en cuanto a sus magnitudes (sus distancias desde el origen), pero dos números complejos distintos pueden tener la misma magnitud, así, por ejemplo, no podemos decir si\(1\) es mayor que\(i\) o\(i\) es mayor que\(1\).

Ejemplo 27: Una raíz cuadrada de\(i\)

\ (i\) "> \(\triangleright\)Demostrar que\(1/\sqrt{2}+i/\sqrt{2}\) es una raíz cuadrada de\(i\). \(\triangleright\)Nuestra prueba puede utilizar cualquier regla ordinaria de aritmética, excepto para ordenar. \[\begin{align*} (\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}})^2 & = \frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} +\frac{1}{\sqrt{2}}\cdot\frac{i}{\sqrt{2}} +\frac{i}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} +\frac{i}{\sqrt{2}}\cdot\frac{i}{\sqrt{2}} \\ &= \frac{1}{2}(1+i+i-1) \\ &= i \end{align*}\] El Ejemplo 27 mostró un método de multiplicación de números complejos. Sin embargo, hay otra interpretación agradable de la multiplicación compleja. Definimos el argumento de un número complejo como su ángulo en el plano complejo, medido en sentido antihorario desde el eje real positivo. Multiplicar dos números complejos corresponde entonces a multiplicar sus magnitudes y sumar sus argumentos. v/Un número complejo puede describirse en términos de su magnitud y argumento. w/El argumento de\(uv\) es la suma de los argumentos de\(u\) y\(v\).

autocomprobación:

Utilizando esta interpretación de la multiplicación, ¿cómo se podrían encontrar las raíces cuadradas de un número complejo? (respuesta en la parte posterior de la versión PDF del libro)

Ejemplo 28: Una identidad

La magnitud\(|z|\) de un número complejo\(z\) obedece a la identidad\(|z|^2=z\bar{z}\). Para probarlo, primero observamos que\(\bar{z}\) tiene la misma magnitud que\(z\), ya que voltearlo al otro lado del eje real no cambia su distancia con respecto al origen. Multiplicar\(z\) por\(\bar{z}\) da un resultado cuya magnitud se encuentra multiplicando sus magnitudes, por lo que la magnitud de\(z\bar{z}\) debe por lo tanto ser igual\(|z|^2\). Ahora sólo tenemos que demostrar que\(z\bar{z}\) es un número real positivo. Pero si, por ejemplo,\(z\) se encuentra en sentido antihorario desde el eje real, entonces\(\bar{z}\) se encuentra en sentido horario desde él. Si\(z\) tiene un argumento positivo, entonces\(\bar{z}\) tiene uno negativo, o viceversa. Por lo tanto, la suma de sus argumentos es cero, por lo que el resultado tiene un argumento de cero, y está en el eje real positivo. ^4 Todo este sistema se construyó con el fin de que cada número tuviera raíces cuadradas. ¿Qué pasa con las raíces cubitas, las cuartas raíces, etc.? ¿Se pone aún más raro cuando quieres hacer esos también? No. El complejo sistema de números que ya hemos discutido es suficiente para manejar todos ellos. La forma más agradable de pensarlo es en términos de raíces de polinomios. En el sistema de números reales, el polinomio\(x^2-1\) tiene dos raíces, es decir, dos valores de\(x\) (más y menos uno) que podemos conectar al polinomio y obtener cero. Debido a que tiene estas dos raíces reales, podemos reescribir el polinomio como\((x-1)(x+1)\). Sin embargo, el polinomio no\(x^2+1\) tiene raíces reales. Es feo que en el sistema de números reales, algunos polinomios de segundo orden tengan dos raíces, y puedan factorizarse, mientras que otros no. En el complejo sistema numérico, todos pueden. Por ejemplo,\(x^2+1\) tiene raíces\(i\) y\(-i\), y se puede factorizar como\((x-i)(x+i)\). En general, el teorema fundamental del álgebra establece que en el complejo sistema numérico, cualquier polinomio de orden n puede ser factorizado completamente en factores\(n\) lineales, y también podemos decir que tiene raíces\(n\) complejas, entendiendo que algunas de las raíces pueden ser las mismas. Por ejemplo, el polinomio de cuarto orden se\(x^4+x^2\) puede factorizar como\((x-i)(x+i)(x-0)(x-0)\), y decimos que tiene cuatro raíces,\(i\),\(-i\), 0, y 0, dos de las cuales resultan ser iguales. Esta es una manera sensata de pensarlo, porque en la vida real, los números son siempre aproximaciones de todos modos, y si hacemos pequeños cambios aleatorios a los coeficientes de este polinomio, tendrá cuatro raíces distintas, de las cuales dos simplemente pasan a estar muy cerca de cero.

Preguntas de Discusión

◊ Encontrar\(\arg i\),\(\arg(-i)\), y\(\arg 37\), donde\(\arg z\) denota el argumento del número complejo\(z\).

◊ Visualizar las siguientes multiplicaciones en el plano complejo utilizando la interpretación de la multiplicación en términos de multiplicar magnitudes y sumar argumentos:\((i)(i)=-1\),\((i)(-i)=1\),\((-i)(-i)=-1\).

◊ Si visualizamos\(z\) como un punto en el plano complejo, ¿cómo debemos visualizar\(-z\)? ¿Qué significa esto en términos de argumentos? Dar interpretaciones similares para\(z^2\) y\(\sqrt{z}\).

◊ Encuentra cuatro números complejos diferentes de\(z\) tal manera que\(z^4=1\).

◊ Calcuta lo siguiente. Usa la magnitud y el argumento, no las partes reales e imaginarias.

\[\begin{equation*} |1+i| , \arg(1+i) , \left|\frac{1}{1+i}\right| , \arg\left(\frac{1}{1+i}\right) , \end{equation*}\]

Con base en los resultados anteriores, computar las partes real e imaginaria de\(1/(1+i)\).

10.5.6 Fórmula de Euler

y/Leonhard Euler (1707-1783).

Habiendo ampliado nuestros horizontes para incluir los números complejos, es natural querer extender funciones que conocíamos y amamos del mundo de los números reales para que también puedan operar en números complejos. La única manera realmente natural de hacer esto en general es usar la serie Taylor. Algo particularmente hermoso sucede con las funciones\(e^x\),\(\sin x\), y\(\cos x\):

\[\begin{align*} e^x &= 1 + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + ... \\ \cos x &= 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - ... \\ \sin x &= x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - ... \end{align*}\]

Si\(x=i\phi\) es un número imaginario, tenemos

\[\begin{equation*} e^{i\phi} = \cos \phi + i \sin \phi , \end{equation*}\]

un resultado conocido como fórmula de Euler. La interpretación geométrica en el plano complejo se muestra en la figura x.

x/El número complejo\(e^{i\phi}\) se encuentra en el círculo unitario.

Aunque el resultado puede parecer algo sacado de un espectáculo de fenómenos al principio, aplicar la definición de la función exponencial deja claro lo natural que es:

\[\begin{align*} e^x = \lim_{n\rightarrow \infty} \left(1+\frac{x}{n}\right)^n . \end{align*}\]

Cuando\(x=i\phi\) es imaginario, la cantidad\((1+i\phi/n)\) representa un número que se encuentra justo por encima de 1 en el plano complejo. Para grandes\(n\),\((1+i\phi/n)\) se vuelve muy cerca del círculo unitario, y su argumento es el ángulo pequeño\(\phi/n\). Elevar este número a la enésima potencia multiplica su argumento por\(n\), dando un número con un argumento de\(\phi\).

La fórmula de Euler se utiliza frecuentemente en física e ingeniería.

Ejemplo 29: Funciones trig en términos de exponenciales complejos
\(\triangleright\)Escribir las funciones seno y coseno en términos de exponenciales. \(\triangleright\)La fórmula de Euler para\(x=-i\phi\) da\(\cos \phi - i \sin \phi\), ya que\(\cos(-\theta)=\cos\theta\), y\(\sin(-\theta)=-\sin\theta\). \[\begin{align*} \cos x &= \frac{e^{ix}+e^{-ix}}{2} \\ \sin x &= \frac{e^{ix}-e^{-ix}}{2i} \end{align*}\]

Ejemplo 30: Una integral dura fácil

\(\triangleright\)Evaluar \[\begin{equation*} \int e^x \cos x dx \end{equation*}\] \(\triangleright\)Esta integral aparentemente imposible se vuelve fácil si reescribimos el coseno en términos de exponenciales: \[\begin{align*} \int e^x & \cos x dx \\ &= \int e^x \left(\frac{e^{ix}+e^{-ix}}{2}\right) dx \\ &= \frac{1}{2} \int (e^{(1+i)x}+e^{(1-i)x})dx \\ &= \frac{1}{2} \left( \frac{e^{(1+i)x}}{1+i}+\frac{e^{(1-i)x}}{1-i} \right)+ c \end{align*}\] Dado que este resultado es la integral de una función de valor real, nos gustaría que fuera real, y de hecho lo es, ya que el primer y segundo términos son conjugados complejos entre sí. Si quisiéramos, podríamos usar el teorema de Euler para convertirlo de nuevo en un resultado manifiestamente real. ^5

10.5.7 Impedancia

Hasta el momento hemos estado pensando en términos de las oscilaciones libres de un circuito. Esto es como un oscilador mecánico que ha sido pateado pero que luego se ha dejado oscilar por sí solo sin ninguna fuerza externa para evitar que las vibraciones se desvanezcan. Supongamos que un circuito LRC es accionado con un voltaje sinusoidalmente variable, tal como ocurrirá cuando un sintonizador de radio está conectado a una antena receptora. Sabemos que una corriente fluirá en el circuito, y sabemos que habrá un comportamiento resonante, pero no es necesariamente sencillo relacionar corriente con voltaje en el caso más general. Empecemos en cambio con los casos especiales de los circuitos LRC que consisten solo en una resistencia, solo una capacitancia, o solo una inductancia. Nos interesa únicamente la respuesta del estado estacionario.

El caso puramente resistivo es fácil. La ley de Ohm da

\[\begin{equation*} I = \frac{V}{R} . \end{equation*}\]

En el caso puramente capacitivo, la relación nos\(V=q/C\) permite calcular

\[\begin{align*} I &= \frac{dq}{dt} \\ &= C \frac{dV}{dt} . \end{align*}\]

Esto es en parte análogo a la ley de Ohm. Por ejemplo, si duplicamos la amplitud de una tensión de CA que varía sinusoidalmente, la derivada también\(dV/dt\) se duplicará, y la amplitud de la corriente sinusoidalmente variable también se duplicará. Sin embargo, no es cierto que\(I=V/R\), debido a que tomar la derivada de una función sinusoidal desplaza su fase 90 grados. Si el voltaje varía como, por ejemplo\(V(t)=V_\text{o}\sin (\omega t)\), entonces la corriente será\(I(t)=\omega C V_\text{o}\cos (\omega t)\). La amplitud de la corriente es\(\omega C V_\text{o}\), que es proporcional a\(V_\text{o}\), pero no es cierto que\(I(t)=V(t)/R\) para alguna constante\(R\).

z/En un condensador, la corriente está\(90°\) por delante del voltaje en fase.

Un segundo problema que surge es que todo nuestro análisis de los circuitos resistivos de CC se construyó sobre la base de la regla de bucle y la regla de unión, las cuales son declaraciones sobre sumas. Para aplicar la regla de unión a un circuito de CA, para exampe, diríamos que la suma de las ondas sinusoidales que describen las corrientes que entran en la unión es igual (en cada momento en el tiempo) a la suma de las ondas sinusoidales que salen. Ahora las funciones sinusoidales tienen una propiedad notable, que es que si se agregan dos funciones sinusoidales diferentes que tienen la misma frecuencia, el resultado también es una sinusoide con esa frecuencia. Por ejemplo,\(\cos\omega t+\sin\omega t=\sqrt{2}\sin(\omega t+\pi/4)\), que se puede probar usando identidades trigonométricas. Las identidades trigonométricas pueden llegar a ser muy engorrosas, sin embargo, y hay una técnica mucho más fácil que involucra números complejos.

aa/Representando funciones con puntos en coordenadas polares.

La figura aa muestra una manera útil de visualizar lo que está pasando. Cuando un circuito está oscilando a una frecuencia\(\omega\), utilizamos puntos en el plano para representar funciones sinusoidales con varias fases y amplitudes.

autocomprobación:

¿Cuál de las siguientes funciones se puede representar de esta manera? \(\cos(6t-4)\),\(\cos^2t\),\(\tan t\) (respuesta al dorso de la versión PDF del libro)

Los ejemplos más simples de cómo visualizar esto en coordenadas polares son unos como\(\cos \omega t+\cos \omega t=2\cos \omega t\), donde todo tiene la misma fase, por lo que todos los puntos se encuentran a lo largo de una sola línea en la gráfica polar, y la suma es igual que sumar números en la recta numérica. El ejemplo menos trivial\(\cos\omega t+\sin\omega t=\sqrt{2}\sin(\omega t+\pi/4)\), se puede visualizar como en la figura ab.

ab/Agregar dos funciones sinusoidales.

La figura ab sugiere que todo esto puede estar amarrado muy bien si identificamos nuestro plano con el plano de números complejos. Por ejemplo, los números complejos 1 y\(i\) representan las funciones\(\sin\omega t\) y\(\cos\omega t\). En la figura z, por ejemplo, el voltaje a través del condensador es una onda sinusoidal multiplicada por un número que da su amplitud, por lo que asociamos esa función con un número que\(\tilde{V}\) se encuentra en el eje real. Su magnitud,\(|\tilde{V}|\), da la amplitud en unidades de voltios, mientras que su argumento\(\arg \tilde{V}\), da su ángulo de fase, que es cero. La corriente es un múltiplo de una onda sinusoidal, por lo que la identificamos con un número que\(\tilde{I}\) se encuentra en el eje imaginario. Tenemos\(\arg\tilde{I}=90°\), y\(|\tilde{I}|\) es la amplitud de la corriente, en unidades de amperios. Pero comparando con nuestro resultado anterior, tenemos\(|\tilde{I}|=\omega C|\tilde{V}|\). Reuniendo la información de fase y magnitud, tenemos\(\tilde{I}=i\omega C\tilde{V}\). Esto se parece mucho a la ley de Ohm, así que escribimos

\[\begin{equation*} \tilde{I} = \frac{\tilde{V}}{Z_C} , \end{equation*}\]

donde la cantidad

\[\begin{equation*} Z_C = -\frac{i}{\omega C} , \text{[impedance of a capacitor]} \end{equation*}\]

que tiene unidades de ohmios, se llama la impedancia del condensador a esta frecuencia.

Tiene sentido que la impedancia se vuelva infinita a la frecuencia cero. La frecuencia cero significa que tardaría un tiempo infinito antes de que el voltaje cambiara en cualquier cantidad. En otras palabras, esto es como una situación en la que el condensador se ha conectado a través de los terminales de una batería y se le ha permitido establecerse a un estado en el que hay carga constante en ambos terminales. Dado que los campos eléctricos entre las placas son constantes, no hay energía que se agregue o saque del campo. Un condensador que no puede intercambiar energía con ningún otro componente del circuito no es más que un circuito roto (abierto).

Tenga en cuenta que tenemos dos tipos de números complejos: los que representan funciones sinusoidales del tiempo, y los que representan impedancias. Los que representan funciones sinusoidales tienen tildes en la parte superior, que parecen pequeñas ondas sinusoidales.

autocomprobación:

¿Por qué un condensador no puede tener impresa su impedancia junto con su capacitancia? (respuesta en la parte posterior de la versión PDF del libro)

Matemáticas similares (pero esta vez con una integral en lugar de una derivada) da

\[\begin{equation*} Z_L = i\omega L \text{[impedance of an inductor]} \end{equation*}\]

para un inductor. Tiene sentido que el inductor tenga menor impedancia a frecuencias más bajas, ya que a frecuencia cero no hay cambio en el campo magnético a lo largo del tiempo. No se agrega energía ni se libera del campo magnético, por lo que no hay efectos de inducción, y el inductor actúa como un trozo de alambre con una resistencia insignificante. El término “estrangulación” para un inductor se refiere a su capacidad para “ahogar” altas frecuencias.

ac/La corriente a través de un inductor va por detrás del voltaje por un ángulo de fase de\(90°\).

Las relaciones de fase mostradas en las figuras z y ac pueden recordarse usando mi propio mnemotécnico, “eVIL”, que muestra que el voltaje (V) conduce la corriente (I) en un circuito inductivo, mientras que lo contrario es cierto en uno capacitivo. Un mnemotécnico más tradicional es “ELI el hombre ICE”, que utiliza la notación E para emf, un concepto estrechamente relacionado con el voltaje (ver p. 686).

Resumiendo, las impedancias de resistencias, capacitores e inductores son

\[\begin{align*} Z_R &= R\\ Z_C &= -\frac{i}{\omega C}\\ Z_L &= i\omega L . \end{align*}\]

Ejemplo 31: Filtros paso bajo y paso alto

Un circuito LRC solo responde a un cierto rango (banda) de frecuencias centradas alrededor de su frecuencia resonante. Como filtro, esto se conoce como filtro de paso de banda. Si bajas tanto los graves como los agudos en tu estéreo, has creado un filtro de paso de banda. Para crear un filtro paso alto o paso bajo, solo necesitamos insertar un condensador o inductor, respectivamente, en serie. Por ejemplo, se podría construir un protector contra sobretensiones muy básico para una computadora insertando un inductor en serie con la computadora. La potencia deseada de 60 Hz de la pared es relativamente baja en frecuencia, mientras que las sobretensiones que pueden dañar tu computadora muestran una variación de tiempo mucho más rápida. Incluso si las sobretensiones no son señales sinusoidales, podemos pensar en un rápido “pico” cualitativamente como si fuera muy alto en frecuencia —como una onda sinusoidal de alta frecuencia, cambia muy rápidamente. Los inductores tienden a ser elementos de circuito grandes, pesados y caros, por lo que es más probable que un simple protector contra sobretensiones consista en un condensador en paralelo con la computadora. (De hecho, uno normalmente solo conectaría un lado del circuito de alimentación a tierra a través de un condensador). El condensador tiene una impedancia muy alta a la baja frecuencia de la señal deseada de 60 Hz, por lo que sifona muy poco de la corriente. Pero para una señal de alta frecuencia, la impedancia del condensador es muy pequeña, y actúa como un camino fácil de impedancia cero hacia el que se desvía la corriente. Lo principal a tener cuidado con la impedancia es que (1) el concepto solo se aplica a un circuito que está siendo accionado sinusoidalmente, (2) la impedancia de un inductor o condensador depende de la frecuencia.

Pregunta de Discusión

◊ La figura z en la página 607 muestra el voltaje y la corriente de un condensador. Esboce el\(t\) gráfico\(q\) - y utilícelo para dar una explicación física de la relación de fase entre el voltaje y la corriente. Por ejemplo, ¿por qué la corriente es cero cuando la tensión está en un máximo o mínimo?

◊ La figura ac en la página 609 muestra el voltaje y la corriente para un inductor. La potencia se considera positiva cuando se pone energía en el campo magnético del inductor. Esboce la gráfica de la potencia, y luego la gráfica de\(U\), la energía almacenada en el campo magnético, y utilícela para dar una explicación física del\(P\) -\(t\) gráfico. En particular, discuta por qué la frecuencia se duplica en la\(t\) gráfica\(P\) -.

◊ Relacionar las características de la gráfica en la figura ac en la página 609 con la historia contada en caricaturas en la figura m /2-3 en la página 598.

10.5.8 Poder

¿Cuánta energía se entrega cuando se aplica un voltaje oscilante a una impedancia? La ecuación\(P=IV\) es generalmente cierta, ya que el voltaje se define como energía por unidad de carga, y la corriente se define como carga por unidad de tiempo: multiplicarlos da energía por unidad de tiempo. En un circuito de CC, las tres cantidades fueron constantes, pero en un circuito oscilante (CA), las tres muestran variación de tiempo.

Una resistencia

Primero examinemos el caso de una resistencia. Por ejemplo, probablemente estés leyendo este libro a partir de una hoja de papel iluminada por una bombilla brillante, que es impulsada por un voltaje oscilante con amplitud\(V_\text{o}\). En el caso especial de una resistencia, lo sabemos\(I\) y\(V\) estamos en fase. Por ejemplo, si\(V\) varía como\(V_\text{o}\cos \omega t\), entonces\(I\) será un coseno también,\(I_\text{o}\cos \omega t\). El poder es entonces\(I_\text{o}V_\text{o}\cos^2\omega t\), que siempre es positivo, ⁶ y varía entre 0 y\(I_\text{o}V_\text{o}\). Incluso si la variación de tiempo fuera\(\cos\omega t\) o\(\sin(\omega t+\pi/4)\), seguiríamos teniendo una potencia máxima de\(I_\text{o}V_\text{o}\), porque tanto el voltaje como la corriente alcanzarían sus máximos al mismo tiempo. En una bombilla, el momento de máxima potencia es cuando el circuito está calentando más rápidamente el filamento. En el instante en que\(P=0\), un cuarto de ciclo después, no fluye corriente, y ninguna energía eléctrica se está convirtiendo en calor. A lo largo de todo el ciclo, el filamento se está deshaciendo de la energía al irradiar luz. ⁷ Dado que el circuito oscila a una frecuencia ⁸ de\(60\ \text{Hz}\), la temperatura realmente no tiene tiempo para subir o bajar mucho durante el período de 1/60 s de la oscilación, y no notamos ninguna variación significativa en el brillo de la luz , incluso con una fotografía de corta exposición.

ad/Potencia en una resistencia: la velocidad a la que la energía eléctrica se convierte en calor.

Así, lo que realmente queremos saber es la potencia promedio, “promedio” es decir, la media a lo largo de un ciclo completo. Ya que estamos cubriendo todo un ciclo con nuestro promedio, no importa qué fase asumamos. Usemos un coseno. La cantidad total de energía transferida a lo largo de un ciclo es

\[\begin{align*} E &= \int dE \\ &= \int_0^T \frac{dE}{dt} dt , \\ \text{where $T=2\pi/\omega$ is the period.} E &= \int_0^T P dt \\ &= \int_0^T P dt \\ &= \int_0^T I_\text{o}V_\text{o} \cos^2\omega t dt \\ &= I_\text{o}V_\text{o} \int_0^T \cos^2\omega t dt \\ &= I_\text{o}V_\text{o} \int_0^T \frac{1}{2} \left(1+\cos 2\omega t\right) dt \\ \text{The reason for using the trig identity $\cos^2 x=(1+\cos 2 x)/2$ in the last step is that it lets us get the answer without doing a hard integral. Over the course of one full cycle, the quantity $\cos 2\omega t$ goes positive, negative, positive, and negative again, so the integral of it is zero. We then have} E &= I_\text{o}V_\text{o} \int_0^T \frac{1}{2} dt \\ &= \frac{I_\text{o}V_\text{o}T}{2} \end{align*}\]

La potencia promedio es

\[\begin{align*} P_{av} &= \frac{\text{energy transferred in one full cycle}}{\text{time for one full cycle}} \\ &= \frac{I_\text{o}V_\text{o}T/2}{T} \\ &= \frac{I_\text{o}V_\text{o}}{2} ,\\ \end{align*}\]

es decir, el promedio es la mitad del máximo. El poder varía de\(0\) a\(I_\text{o}V_\text{o}\), y pasa cantidades iguales de tiempo por encima y por debajo del máximo, por lo que no es de extrañar que la potencia promedio esté a medio camino entre cero y la máxima. Resumiendo, tenemos

\[\begin{align*} P_{av} &= \frac{I_\text{o}V_\text{o}}{2} \text{[average power in a resistor]}\\ \end{align*}\]

para una resistencia.

Cantidades RMS

Supongamos que un día la compañía eléctrica decidió comenzar a suministrar su electricidad como CC en lugar de CA. ¿Cómo se tendría que relacionar el voltaje de CC con la amplitud\(V_\text{o}\) de la tensión de CA utilizada anteriormente si quisieran que sus bombillas tuvieran el mismo brillo que antes? La resistencia de la bombilla,\(R\), es un valor fijo, por lo que necesitamos relacionar la potencia con la tensión y la resistencia, eliminando la corriente. En el caso DC, esto da\(P=IV=(V/R)V=V^2/R\). (Para DC,\(P\) y\(P_{av}\) son los mismos.) En el caso AC,\(P_{av} = I_\text{o}V_\text{o}/2=V_\text{o}^2/2R\). Dado que no hay factor de 1/2 en el caso de CC, la misma potencia podría proporcionarse con un voltaje de CC que era menor en un factor de\(1/\sqrt{2}\). A pesar de que escuchará a la gente decir que el voltaje doméstico en Estados Unidos es de 110 V, su amplitud es en realidad\((110\ \text{V})\times\sqrt{2}\approx160\ \text{V}\). La razón para referirse\(V_\text{o}/\sqrt{2}\) como “el” voltaje es que las personas que son ingenuas sobre los circuitos de CA pueden conectarse\(V_\text{o}/\sqrt{2}\) a una ecuación de CC familiar como\(P=V^2/R\) y obtener la respuesta promedio correcta. A la cantidad\(V_\text{o}/\sqrt{2}\) se le llama voltaje “RMS”, que significa “raíz cuadrática media”. La idea es que si cuadras la función\(V(t)\), tomes su promedio (media) a lo largo de un ciclo, y luego tomas la raíz cuadrada de esa media, obtienes\(V_\text{o}/\sqrt{2}\). Muchos medidores digitales proporcionan lecturas RMS para medir tensiones y corrientes de CA.

Un condensador

Para un condensador, el cálculo comienza igual, pero termina con un giro. Si el voltaje varía como coseno\(V_\text{o}\cos \omega t\), entonces la relación nos\(I=CdV/dt\) dice que la corriente será alguna constante multiplicada por menos el seno,\(-V_\text{o}\sin \omega t\). La integral que hicimos en el caso de una resistencia ahora se convierte

\[\begin{equation*} E = \int_0^T -I_\text{o}V_\text{o} \sin \omega t \cos \omega t dt ,\\ \end{equation*}\]

y basado en la figura ae, puedes convencerte fácilmente de que en el transcurso de un ciclo completo, la potencia gasta dos cuartos de ciclo siendo negativo y dos siendo positivo. En otras palabras, ¡la potencia promedio es cero!

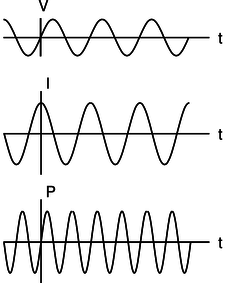
ae/Potencia en un condensador: la velocidad a la que se almacena la energía en (+) o se elimina de (-) el campo eléctrico.

¿Por qué es esto? Tiene sentido si piensas en términos de energía. Una resistencia convierte la energía eléctrica en calor, nunca al revés. Un condensador, sin embargo, simplemente almacena energía eléctrica en un campo eléctrico y luego la devuelve. Para un condensador,

\[\begin{align*} P_{av} &= 0 \text{[average power in a capacitor]}\\ \end{align*}\]

Observe que aunque la potencia promedio es cero, la potencia en cualquier instante dado no suele ser cero, como se muestra en la figura ae. El condensador sí transfiere energía: es solo que después de tomar prestada algo de energía, siempre la devuelve en el siguiente cuarto de ciclo.

Un inductor

El análisis para un inductor es similar al de un condensador: la potencia promediada en un ciclo es cero. Nuevamente, simplemente estamos almacenando energía temporalmente en un campo (esta vez un campo magnético) y recuperándola más tarde.

10.5.9 Coincidencia de impedancia

af/Deseamos maximizar la potencia entregada a la carga,\(Z_\text{o}\), ajustando su impedancia.

La figura af muestra una situación común: deseamos maximizar la potencia promedio\(P_{av}\), entregada a la carga para un valor fijo de\(V_\text{o}\), la amplitud de la tensión de accionamiento oscilante. Suponemos que la impedancia de la línea de transmisión,\(Z_T\) es un valor fijo, sobre el cual no tenemos control, pero somos capaces de diseñar la carga,\(Z_\text{o}\), con cualquier impedancia que nos guste. Por ahora, también asumiremos que ambas impedancias son resistivas. Por ejemplo,\(Z_T\) podría ser la resistencia de un cable de extensión largo, y\(Z_\text{o}\) podría ser una lámpara al final del mismo. El resultado se generaliza inmediatamente, sin embargo, a cualquier tipo de impedancia. Por ejemplo, la carga podría ser la bobina magnética de un altavoz estéreo, que muestra tanto la inductancia como la resistencia. (Para una carga puramente inductiva o capacitiva,\(P_{av}\) equivale a cero, ¡así que el problema no es muy interesante!)

Como suponemos que tanto la carga como la línea de transmisión son resistivas, sus impedancias se suman en serie, y la amplitud de la corriente viene dada por

\[\begin{align*} I_\text{o} &= \frac{V_\text{o}}{Z_\text{o}+Z_T} ,\\ \text{so} P_{av} &= I_\text{o}V_\text{o}/2 \\ &= I_\text{o}^2Z_\text{o}/2 \\ &= \frac{V_\text{o}^2Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}/2 . \text{The maximum of this expression occurs where the derivative is zero,} 0 &= \frac{1}{2}\frac{d}{dZ_\text{o}}\left[\frac{V_\text{o}^2Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}\right] \\ 0 &= \frac{1}{2}\frac{d}{dZ_\text{o}}\left[\frac{Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}\right] \\ 0 &= \left(Z_\text{o}+Z_T\right)^{-2}-2Z_\text{o}\left(Z_\text{o}+Z_T\right)^{-3} \\ 0 &= \left(Z_\text{o}+Z_T\right)-2Z_\text{o} \\ Z_\text{o} &= Z_T \end{align*}\]

En otras palabras, para maximizar la potencia entregada a la carga, debemos hacer que la impedancia de la carga sea la misma que la de la línea de transmisión. Este resultado puede parecer sorprendente al principio, pero tiene sentido si lo piensas bien. Si la impedancia de la carga es demasiado alta, es como abrir un interruptor y romper el circuito; no se suministra energía. Por otro lado, no paga hacer que la impedancia de la carga sea demasiado pequeña. Hacerlo más pequeño sí da más corriente, pero no importa cuán pequeña la hagamos, la corriente seguirá estando limitada por la impedancia de la línea de transmisión. A medida que la impedancia de la carga se acerca a cero, la corriente se acerca a este valor fijo, y la potencia entregada\(I_\text{o}^2Z_\text{o}\),, disminuye en proporción a\(Z_\text{o}\).

Maximizar la transmisión de potencia haciendo coincidir con\(Z_T\)\(Z_\text{o}\) se llama coincidencia de impedancia. Por ejemplo, un altavoz estéreo doméstico de 8 ohmios se emparejará correctamente con un amplificador estéreo doméstico con una impedancia interna de 8 ohmios, y los altavoces de automóvil de 4 ohmios se emparejarán correctamente con un estéreo de automóvil con una impedancia interna de 4 ohmios. Se podría pensar que la coincidencia de impedancia no sería importante porque incluso si, por ejemplo, usáramos un estéreo de automóvil para conducir altavoces de 8 ohmios, podríamos compensar el desajuste simplemente girando la perilla de volumen más alto. De hecho, esta es una forma de compensar cualquier desajuste de impedancia, pero siempre hay un precio que pagar. Cuando las impedancias coinciden, la mitad de la potencia se disipa en la línea de transmisión y la mitad en la carga. Al conectar un amplificador de 4 ohmios a un altavoz de 8 ohmios, sin embargo, estarías configurando una situación en dos vatios se estaban disipando como calor dentro del amplificador por cada amplificador que se entregaba al altavoz. En otras palabras, estarías desperdiciando energía, y quizás quemando tu amplificador cuando subas el volumen para compensar el desajuste.

10.5.10 Impedancias en serie y paralelo

¿Cómo se combinan las impedancias en serie y en paralelo? La belleza de tratarlos como números complejos es que simplemente se combinan de acuerdo con las mismas reglas que ya aprendiste como resistencias.

Ejemplo 32: Impedancia en serie

\(\triangleright\)Un condensador y un inductor en serie entre sí son impulsados por un voltaje sinusoidalmente oscilante. ¿A qué frecuencia se maximiza la corriente? \(\triangleright\)Impedancias en serie, como resistencias en serie, agregan. El condensador y el inductor actúan como si fueran un elemento de circuito único con una impedancia \[\begin{align*} Z &= Z_{L}+ Z_{C}\\ &= i\omega L-\frac{ i}{\omega C} .\\ \text{The current is then} \tilde{ I} = \frac{\tilde{ V}}{ i\omega L- i/\omega C} . \end{align*}\] No nos importa la fase de la corriente, solo su amplitud, que está representada por el valor absoluto del número complejo\(\tilde{ I}\), y esto se puede maximizar haciendo lo más pequeño\(| i\omega L- i/\omega C|\) posible. Pero hay cierta frecuencia en la que esta cantidad es cero — \[\begin{gather*} 0 = i\omega L-\frac{ i}{\omega C}\\ \frac{1}{\omega C} = \omega L\\ \omega = \frac{1}{\sqrt{ LC}} \end{gather*}\] ¡A esta frecuencia, la corriente es infinita! ¿Qué está pasando físicamente? Este es un circuito LRC con\(R=0\). Tiene una resonancia a esta frecuencia, y debido a que no hay amortiguación, la respuesta a la resonancia es infinita. Por supuesto, cualquier circuito LRC real tendrá alguna amortiguación, por pequeña que sea (cf. figura j en la página 181).

Ejemplo 33: Resonancia con amortiguación

\(\triangleright\)¿Cuál es la amplitud de la corriente en un circuito LRC en serie? \(\triangleright\)Generalizando del ejemplo 32, agregamos una tercera impedancia real: \[\begin{align*} |\tilde{ I}| &= \frac{|\tilde{ V}|}{| Z|} \\ &= \frac{|\tilde{ V}|}{| R+ i\omega L- i/\omega C|} \\ &= \frac{|\tilde{ V}|}{\sqrt{ R^2+(\omega L-1/\omega C)^2}} \end{align*}\] ¡Este resultado habría tomado páginas de álgebra sin la técnica de números complejos!

Ejemplo 34: Un filtro cruzado estéreo de segundo orden

Un filtro crossover estéreo asegura que las frecuencias altas vayan al tweeter y los bajos al woofer. Esto se puede lograr simplemente poniendo un solo condensador en serie con el tweeter y un solo inductor en serie con el woofer. Sin embargo, dicho filtro no corta muy bruscamente. Supongamos que modelamos los altavoces como resistencias. (Realmente también tienen inductancia, ya que tienen bobinas en ellas que sirven como electroimanes para mover el diafragma que hace el sonido). Entonces el poder que extraen es\(I^2 R\). Poner un inductor en serie con el woofer, ag /1, da una impedancia total que a altas frecuencias está dominada por los inductores, por lo que la corriente es proporcional a\(\omega^{-1}\), y la potencia extraída por el woofer es proporcional a\(\omega^{-2}\). ag/Ejemplo 34. Un filtro de segundo orden, como ag /2, es aquel que corta más bruscamente: a altas frecuencias, la potencia va como\(\omega^{-4}\). Para analizar este circuito, primero calculamos la impedancia total: \[\begin{equation*} Z = Z_{L}+( Z_{C}^{-1}+ Z_R^{-1})^{-1} \end{equation*}\] Toda la corriente pasa a través del inductor, así que si el voltaje de conducción que se suministra a la izquierda es\(\tilde{ V}_d\), tenemos \[\begin{equation*} \tilde{ V}_d = \tilde{ I}_{L} Z , \end{equation*}\] y también tenemos \[\begin{equation*} \tilde{ V}_{L} = \tilde{ I}_{L} Z_L . \end{equation*}\] La regla de bucle, aplicada al perímetro exterior del circuito, da \[\begin{equation*} \tilde{ V}_{d} = \tilde{ V}_{L}+\tilde{ V}_R . \end{equation*}\] Álgebra sencilla ahora da como resultado \[\begin{equation*} \tilde{ V}_{R} = \frac{\tilde{ V}_{d}}{1+ Z_L/ Z_{C}+ Z_{L}/ Z_R} . \end{equation*}\] A altas frecuencias, el\(Z_{L}/ Z_C\) término, que varía como\(\omega^2\), domina, así\(\tilde{ V}_R\) y\(\tilde{ I}_R\) son proporcionales a\(\omega^{-2}\), y la potencia es proporcional a\(\omega^{-4}\).

Colaboradores y Atribuciones

Template:ContribCrowell