11.E: Campos (Ejercicios)

1. El espacio entre los electrodos en la bujía de un motor de automóvil es de 0.060 cm. Para producir una chispa eléctrica en una mezcla gasolina-aire, se debe lograr un campo eléctrico de\(3.0\times10^6\) V/m. Al arrancar un automóvil, ¿qué voltaje mínimo debe suministrar el circuito de encendido? Supongamos que el campo es uniforme. (consulta de respuesta disponible en lightandmatter.com)

(b) El pequeño tamaño del espacio entre los electrodos es inconveniente porque puede bloquearse fácilmente y se necesitan herramientas especiales para medirlo. ¿Por qué no diseñan bujías con un espacio más amplio?

2. a) Como se sugiere en el ejemplo 9 de la página 573, utilizar aproximaciones para mostrar que la expresión dada para el campo eléctrico se aproxima\(kQ/d^2\) para grandes\(d\).
b) Hacer lo mismo para el resultado del ejemplo 12 de la página 577.

3. Los astrónomos creen que la distribución de masas (masa por unidad de volumen) de algunas galaxias puede aproximarse, en coordenadas esféricas, por\(\rho=ae^{-br}\), para\(0\le r\le\infty\), dónde\(\rho\) está la densidad. Encuentra la masa total.

4. (a) En el momento\(t=0\), se coloca una partícula cargada positivamente, en reposo, en vacío, en el que existe un campo eléctrico uniforme de magnitud\(E\). Escribir una ecuación dando la velocidad de la partícula\(v\),, en términos de\(t\)\(E\), y su masa y carga\(m\) y\(q\). (cheque de respuesta disponible en lightandmatter.com)
(b) Si esto se hace con dos objetos diferentes y se observa que tienen el mismo movimiento, ¿qué se puede concluir sobre sus masas y cargas? (Por ejemplo, cuando se descubrió la radiactividad, se encontró que una forma de la misma tenía el mismo movimiento que un electrón en este tipo de experimentos.)

5. Mostrar que la definición alternativa de la magnitud del campo eléctrico,\(|E|=\tau/D_t\sin\theta\), tiene unidades que tienen sentido.

6. Rehaga el cálculo del ejemplo 5 en la página 566 usando un origen diferente para el sistema de coordenadas, y demuestre que obtiene el mismo resultado.

7. La definición del momento dipolo,\(\mathbf{D}=\sum q_i \mathbf{r}_i\), implica que el vector\(\mathbf{r}_i\) se extiende desde el origen de nuestro sistema de coordenadas hasta la carga\(q_i\). Claramente hay casos en los que esto hace que el momento dipolar dependa de la elección del sistema de coordenadas. Por ejemplo, si solo hay una carga, entonces podríamos hacer que el momento dipolo sea igual a cero si elegimos que el origen esté justo encima de la carga, o distinto de cero si ponemos el origen en otro lugar.
a) Formular un ejemplo numérico con dos cargas de igual magnitud y signo opuesto. Calcular el momento dipolar utilizando dos sistemas de coordenadas diferentes que están orientados de la misma manera, pero difieren en la elección de origen. Comenta el resultado.
b) Generalizar el resultado de la parte a a cualquier par de cargas de igual magnitud y signo opuesto. Se supone que esto es una prueba de cualquier arreglo de los dos cargos, así que no asuma ningún número.
c) Generalizar más, a\(n\) cargos.

a/Problema 8.

8. Compara los dos momentos dipolares.

9. Encuentra un arreglo de cargas que tenga carga total cero y momento dipolo cero, pero que hará que los campos eléctricos no se desvanecen.

10. Como se sugiere en el ejemplo 11 de la página 575, demuestre que puede obtener el mismo resultado para el campo en el eje diferenciando el voltaje

b/Problema 11.

11. Tres cargas están dispuestas en un cuadrado como se muestra. Los tres cargos son positivos. ¿Qué valor de\(q_2/q_1\) producirá campo eléctrico cero en el centro de la plaza? (consulta de respuesta disponible en lightandmatter.com)

12. Se trata de un problema unidimensional, con todo confinado al\(x\) eje. El dipolo A consiste en una carga\(-1.000\) C a\(x=0.000\) m y una carga\(1.000\) C a\(x=1.000\) m. El dipolo B tiene una carga\(-2.000\) C a\(x=0.000\) m y una carga\(2.000\) C en\(x=0.500\) m.
(a) Compara los dos momentos dipolares.
(b) Calcular el campo creado por el dipolo A en\(x=10.000\) m, y comparar con el dipolo de campo B haría. Comenta el resultado. (consulta de respuesta disponible en lightandmatter.com)

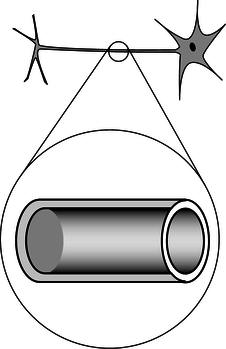
c/Problema 13.

13. En nuestra neurona ya familiar, la diferencia de voltaje entre las superficies interna y externa de la membrana celular está aproximadamente\(V_{out}-V_{in}=-70\ \text{mV}\) en el estado de reposo, y el grosor de la membrana es de aproximadamente 6.0 nm (es decir, solo alrededor de cien átomos de grosor). ¿Cuál es el campo eléctrico dentro de la membrana? (consulta de respuesta disponible en lightandmatter.com)

14. Un protón se encuentra en una región en la que el campo eléctrico viene dado por\(E=a+bx^3\). Si el protón comienza en reposo en\(x_1=0\), encuentra su velocidad,\(v\), cuando alcanza la posición\(x_2\). Da tu respuesta en términos de\(a\),\(b\),\(x_2\),\(e\) y y\(m\), la carga y masa del protón. (consulta de respuesta disponible en lightandmatter.com)

15. (a) Dado que el campo sobre el eje de un dipolo a grandes distancias es proporcional a\(D/r^3\), mostrar que su voltaje varía como\(D/r^2\). (Ignorar los signos positivos y negativos y las constantes numéricas de proporcionalidad.)
(b) Anote una expresión exacta para el voltaje de un dipolo de dos cargas en un punto sobre el eje, sin suponer que la distancia es grande en comparación con el tamaño del dipolo. Tu expresión tendrá que contener las cargas reales y el tamaño del dipolo, no solo su momento dipolo. Ahora usa aproximaciones para mostrar que, a grandes distancias, esto es consistente con tu respuesta a la parte a.\ hwhint {hwhint:dipolev}

16. Un átomo de hidrógeno es eléctricamente neutro, por lo que a grandes distancias, esperamos que cree esencialmente un campo eléctrico cero. Esto no es cierto, sin embargo, cerca del átomo o dentro de él. Muy cerca del protón, por ejemplo, el campo es muy fuerte. Para ver esto, piense en el electrón como una nube esféricamente simétrica que rodea al protón, haciéndose cada vez más delgado a medida que nos alejamos del protón. (La mecánica cuántica nos dice que esta es una imagen más correcta que tratar de imaginar el electrón orbitando el protón.) Cerca del centro del átomo, el campo de la nube de electrones se cancela por simetría, pero el campo del protón es fuerte, por lo que el campo total es muy fuerte. El voltaje dentro y alrededor del átomo de hidrógeno se puede aproximar usando una expresión de la forma\(V=r^{-1}e^{-r}\). (Las unidades salen mal, porque he omitido algunas constantes.) Encuentra el campo eléctrico correspondiente a este voltaje, y comenta su comportamiento en muy grande y muy pequeño\(r\). (solución en la versión pdf del libro)

17. Una molécula de dióxido de carbono está estructurada como O-C-O, con los tres átomos a lo largo de una línea. Los átomos de oxígeno agarran un poco de carga extra negativa, dejando el carbono positivo. La simetría de la molécula, sin embargo, significa que no tiene ningún momento dipolar general, a diferencia de una molécula de agua en forma de V, por ejemplo. Mientras que el voltaje de un dipolo de magnitud\(D\) es proporcional a\(D/r^2\) (ver problema 15), resulta que el voltaje de una molécula de dióxido de carbono en un punto distante a lo largo del eje de la molécula es igual\(b/r^3\), donde\(r\) está la distancia de la molécula y\(b\) es una constante (cf. problema 9). ¿Cuál sería el campo eléctrico de una molécula de dióxido de carbono en un punto del eje de la molécula, a una\(r\) distancia de la molécula? (consulta de respuesta disponible en lightandmatter.com)

18. Un átomo de hidrógeno en un estado particular tiene la densidad de carga (carga por unidad de volumen) de la nube de electrones dada por\(\rho=ae^{-br}z^2\), donde\(r\) está la distancia desde el protón, y\(z\) es la coordenada medida a lo largo del\(z\) eje. Dado que la carga total de la nube de electrones debe ser\(-e\), encontrar\(a\) en términos de las otras variables.

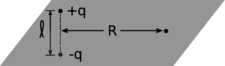
d/Problema 19.

19. Un dipolo tiene un plano medio, es decir, el plano que corta a través del centro del dipolo, y es perpendicular al eje del dipolo. Considere un dipolo de dos cargas hecho de cargas puntuales\(\pm q\) ubicadas en\(z=\pm\ell/2\). Usa aproximaciones para encontrar el campo en un punto distante en el plano medio, y mostrar que su magnitud sale a ser\(kD/R^3\) (la mitad de lo que sería en un punto del eje que se encuentra a igual distancia del dipolo).

e/Problema 20.

20. La figura muestra una cámara de vacío rodeada por cuatro electrodos metálicos en forma de hipérbolas. (Sí, los físicos a veces piden a sus talleres de máquinas universitarias cosas mecanizadas en formas matemáticas como esta. Tienen que hacerse en molinos controlados por computadora.) Suponemos que los electrodos se extienden lejos dentro y fuera de la página a lo largo del\(z\) eje invisible, de manera que por simetría, los campos eléctricos son los mismos para todos\(z\). Por lo tanto, el problema es efectivamente bidimensional. Dos de los electrodos están en voltaje\(+V_\text{o}\), y los otros dos en\(-V_\text{o}\), como se muestra. Las ecuaciones de las superficies hiperbólicas son\(|xy|=b^2\), donde\(b\) es una constante. (Podemos interpretar\(b\) como dar las ubicaciones\(x=\pm b\),\(y=\pm b\) de los cuatro puntos en las superficies que están más cerca del eje central). No hay una manera obvia y peatonal de determinar el campo o voltaje en la región central de vacío, pero hay un truco que funciona: con un poco de conocimiento matemático, vemos que el voltaje\(V=V_\text{o}b^{-2}xy\) es consistente con toda la información dada. (Los matemáticos podrían demostrar que esta solución era única, pero un físico la conoce por motivos físicos: si hubiera dos soluciones diferentes, ¡no habría forma física para que el sistema decida cuál hacer!) a) Utilizar las técnicas de la subsección 10.2.2 para encontrar el campo en la región de vacío, y b) bosquejar el campo como un “mar de flechas”. (consulta de respuesta disponible en lightandmatter.com)

21. (a) Una determinada región del espacio tridimensional tiene una tensión que varía como\(V=br^2\), donde\(r\) está la distancia desde el origen. Utilice las técnicas de la subsección 10.2.2 para encontrar el campo. (verificación de respuesta disponible en lightandmatter.com)
(b) Anote otro voltaje que dé exactamente el mismo campo.

22. (a) El ejemplo 10 de la página 574 da el campo de una varilla cargada en su plano medio. A partir de este resultado, toma el límite a medida que la longitud de la varilla se acerca al infinito. Tenga en cuenta que no\(\lambda\) está cambiando, así como\(L\) se hace más grande, la carga total\(Q\) aumenta. \ hwans {hwans:estrips}
(b) En el texto, he mostrado (por varios métodos diferentes) que es el campo de un plano infinito, uniformemente cargado\(2\pi k\sigma\). Ahora vas a derivar el mismo resultado por un método diferente. Supongamos que es el\(x-y\) avión el que está cargado, y queremos encontrar el campo en el punto\((0,0,z)\). (Dado que el plano es infinito, no hay pérdida de generalidad en asumir\(x=0\) y\(y=0\).) Imagina que cortamos el plano en un número infinito de tiras rectas paralelas al\(y\) eje. Cada tira tiene un ancho infinitesimal\(dx\), y se extiende desde\(x\) hasta\(x+dx\). La contribución de cualquiera de estas tiras al campo en nuestro punto tiene una magnitud que se puede encontrar a partir de la parte A. Por adición vectorial, probar el resultado deseado para el campo del plano de carga.

f/Problema 23.

23. Considere el campo eléctrico creado por una superficie cilíndrica cargada uniformemente que se extiende hasta el infinito en una dirección.
(a) Demostrar que el campo en el centro de la boca del cilindro es\(2\pi k\sigma\), que pasa a ser el mismo que el campo de una hoja plana infinita de carga!
(b) Esta expresión es independiente del radio del cilindro. Explique por qué esto debería ser así. Por ejemplo, ¿qué pasaría si doblaras el radio del cilindro?

24. En una tormenta eléctrica, la nube y el suelo actúan como un condensador de placa paralela, que normalmente se carga debido a la electricidad por fricción en colisiones de partículas de hielo en la atmósfera fría superior. Los rayos se producen cuando la magnitud del campo eléctrico se acumula hasta un valor crítico,\(E_c\), en el que se ioniza el aire.
(a) Tratar la nube como un cuadrado plano con lados de longitud\(L\). Si está a una altura\(h\) sobre el suelo, encuentra la cantidad de energía liberada en el rayo. (verificación de respuesta disponible en lightandmatter.com)
(b) Basado en tu respuesta de la parte a, ¿cuál es más peligrosa, un rayo de una nube de gran altitud o una de baja altitud?
c) Hacer una estimación de orden de magnitud de la energía liberada por un rayo típico, asumiendo valores razonables para su tamaño y altitud. \(E_c\)es de aproximadamente\(10^6\) V/m.

25. (a) ¡Demuestre que la energía en el campo eléctrico de una carga puntual es infinita! ¿La integral diverge a distancias pequeñas, a grandes distancias, o ambas? \ hwhint {hwhint:epointinfty}
[4] (b) Ahora calcula la energía en el campo eléctrico de una esfera uniformemente cargada con radio\(b\). Con base en el teorema de shell, se puede demostrar que el campo para\(r>b\) es el mismo que para una carga puntual, mientras que el campo para\(r\lt b\) es\(kqr/b^3\). (El ejemplo 38 muestra esto usando una técnica diferente).

El cálculo en la parte a parece mostrar que se requeriría energía infinita para crear una partícula cargada, puntual. Sin embargo, hay procesos que, por ejemplo, crean pares electrón-positrón, y estos procesos no requieren energía infinita. Según la famosa ecuación de Einstein\(E=mc^2\), la energía requerida para crear tal par solo debería ser\(2mc^2\), que es finita. Una forma de salir de esta dificultad es asumir que ninguna partícula es realmente puntual, y esta es de hecho la principal motivación detrás de una teoría física especulativa llamada teoría de cuerdas, que postula que las partículas cargadas son en realidad bucles diminutos, no puntos.

(consulta de respuesta disponible en lightandmatter.com)

g/Problema 26.

26. La neurona en la figura ha sido dibujada bastante corta, pero algunas neuronas de tu médula espinal tienen colas (axones) de hasta un metro de largo. Las superficies interna y externa de la membrana actúan como las “placas” de un condensador. (El hecho de que se haya enrollado en un cilindro tiene muy poco efecto.) Para funcionar, la neurona debe crear una diferencia de voltaje\(V\) entre las superficies interna y externa de la membrana. Deje que el grosor, el radio y la longitud de la membrana sean\(t\)\(r\), y\(L\). a) Calcular la energía que se debe almacenar en el campo eléctrico para que la neurona haga su trabajo. (En la vida real, la membrana está hecha de una sustancia llamada dieléctrico, cuyas propiedades eléctricas aumentan la cantidad de energía que debe almacenarse. Por el bien de este análisis, ignore este hecho.) \ hwhint {hwhint:neuronenergy} (consulta de respuestas disponible en lightandmatter.com)
(b) La aptitud evolutiva de un organismo debería ser mejor si necesita menos energía para operar su sistema nervioso. Con base en tu respuesta a la parte a, ¿qué esperarías que hiciera la evolución a las dimensiones\(t\) y\(r?\) qué otras limitaciones evitarían que estas tendencias evolutivas fueran demasiado lejos?

h/Problema 27.

27. La figura muestra vistas en sección transversal de dos condensadores cúbicos, y una vista en sección transversal de los mismos dos condensadores juntos para que sus interiores coincidan. Un condensador con las placas juntas tiene un campo eléctrico casi uniforme entre las placas, y un campo casi cero afuera; estos condensadores no tienen sus placas muy juntas en comparación con las dimensiones de las placas, pero para los fines de este problema, suponga que todavía tienen aproximadamente el tipo de patrón de campo idealizado que se muestra en la figura. Cada condensador tiene un volumen interior de 1.00\(\text{m}^3\), y se carga hasta el punto en que su campo interno es de 1.00 V/m.
(a) Calcular la energía almacenada en el campo eléctrico de cada condensador cuando están separados. (verificación de respuesta disponible en lightandmatter.com)
(b) Calcular la magnitud del campo interior cuando los dos condensadores se juntan de la manera mostrada. Ignorar los efectos que surgen de la redistribución de la carga de cada condensador bajo la influencia del otro condensador. (verificación de respuesta disponible en lightandmatter.com)
(c) Calcular la energía de la configuración de poner juntos. ¿Armarlos así libera energía, consume energía, o tampoco? (consulta de respuesta disponible en lightandmatter.com)

28. Encuentra la capacitancia de la superficie de la tierra, asumiendo que hay una “placa” esférica exterior en el infinito. (En realidad, esta placa exterior solo representaría alguna parte lejana del universo al que nos llevamos parte de la carga de la tierra para cargar la tierra). (consulta de respuesta disponible en lightandmatter.com)

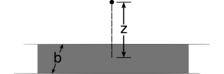
i/Problema 29.

29. (a) Mostrar que el campo que se encuentra en el ejemplo 10 en la página 574 se reduce a\(E=2k\lambda/R\) en el límite de\(L\rightarrow\infty\).
(b) Una franja infinita de ancho\(b\) tiene una densidad de carga superficial\(\sigma\). Encuentra el campo en un punto a una distancia\(z\) de la franja, acostado en el plano bisectando perpendicularmente la tira. (verificación de respuesta disponible en lightandmatter.com)
(c) Mostrar que esta expresión tiene el comportamiento correcto en el límite donde se\(z\) acerca a cero, y también en el límite de\(z\gg b\). Para esto último, necesitarás el resultado del problema 22 a, que se da en la página 930.

30. Un cilindro sólido de radio\(b\) y longitud\(\ell\) se carga uniformemente con una carga total\(Q\). Encuentra el campo eléctrico en un punto en el centro de uno de los extremos planos.

31. Encuentre el voltaje en el borde de un disco con carga uniforme. (\(V=0\)Definir estar infinitamente lejos del disco.) (consulta de respuesta disponible en lightandmatter.com)\ hwhint {hwhint:vedgedisk}

32. Encuentre la energía almacenada en un condensador en términos de su capacitancia y la diferencia de voltaje a través de él. (consulta de respuesta disponible en lightandmatter.com)

33. (a) Encuentre la capacitancia de dos condensadores idénticos en serie.
(b) En base a esto, ¿cómo esperaría que la capacitancia de un condensador de placa paralela dependiera de la distancia entre las placas?

34. (a) Utilizar técnicas de números complejos para reescribir la función\(f(t)=4\sin\omega t+3\cos\omega t\) en el formulario\(A\sin(\omega t+\delta)\). (verificación de respuesta disponible en lightandmatter.com)
(b) Verificar el resultado utilizando la identidad trigonométrica\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\).

35. (a) Demostrar que la ecuación\(V_L=LdI/dt\) tiene las unidades correctas.
b) Verificar que\(RC\) tenga unidades de tiempo.
(c) Verificar que\(L/R\) tenga unidades de tiempo.

36. Encuentra la inductancia de dos inductores idénticos en paralelo.

37. Calcular la cantidad\(i^i\) (es decir, encontrar sus partes reales e imaginarias). (consulta de respuesta disponible en lightandmatter.com)

38. Los cables en sí mismos en un circuito pueden tener resistencia, inductancia y capacitancia. ¿Serían más importantes la inductancia y capacitancia “parásitas” para los circuitos de baja frecuencia o de alta frecuencia? Para simplificar, suponga que los cables actúan como si estuvieran en serie con un inductor o condensador.

39. Partiendo de la relación\(V=LdI/dt\) para la diferencia de voltaje a través de un inductor, mostrar que un inductor tiene una impedancia igual a\(L\omega\).

40. Una caja rectangular se carga uniformemente con una densidad de carga\(\rho\). La caja es extremadamente larga y delgada, y su sección transversal es un cuadrado con lados de largo\(b\). La longitud es tan grande en comparación con\(b\) que podemos considerarla como infinita. Encuentra el campo eléctrico en un punto que se encuentra en la superficie de la caja, en el punto medio entre los dos bordes. Tu respuesta implicará una integral que se realiza más fácilmente usando software de computadora.

41. Una tubería cilíndrica hueca tiene longitud\(\ell\) y radio\(b\). Sus extremos están abiertos, pero en la superficie curva tiene una densidad de carga\(\sigma\). Una carga\(q\) con masa\(m\) se libera en el centro de la tubería, en equilibrio inestable. Debido a que el equilibrio es inestable, la partícula se acclera en una dirección u otra, a lo largo del eje de la tubería, y sale disparando como una bala desde el cañón de una pistola. Encuentra la velocidad de la partícula cuando está infinitamente lejos de la “pistola”. Tu respuesta involucrará una integral que es difícil de hacer a mano; es posible que quieras buscarla en una tabla de integrales, hacerlo en línea en integrals.com, o descargar e instalar el software gratuito Maxima de matemáticas simbólicas de maxima.sourceforge.net.

42. Si un sintonizador de radio FM que consiste en un circuito LRC contiene un\(\mu\text{H}\) inductor 1.0, ¿qué rango de capacitancias debería poder proporcionar el condensador variable? (consulta de respuesta disponible en lightandmatter.com)

43. (a) Encuentre la impedancia paralela de una\(37\ \text{k}\Omega\) resistencia y un condensador de 1.0 nF a\(f=1.0\times10^4\) Hz. (verificación de respuesta disponible en lightandmatter.com)
(b) Un voltaje con una amplitud de 1.0 mV impulsa esta impedancia a esta frecuencia. ¿Cuál es la amplitud de la corriente extraída de la fuente de voltaje, cuál es el ángulo de fase de la corriente con respecto al voltaje, y conduce el voltaje, o se queda atrás? (consulta de respuesta disponible en lightandmatter.com)

44. Un circuito LRC en serie consta de una\(\Omega\) resistencia de 1.000, un condensador de 1.000 F y un inductor de 1.000 H. (¡Estos no son valores particularmente fáciles de encontrar en la estantería de Radio Shack!)
a) Trazar su impedancia como punto en el plano complejo para cada una de las siguientes frecuencias:\(\omega\) =0.250, 0.500, 1.000, 2.000 y 4.000 Hz.
(b) ¿Cuál es la frecuencia angular resonante\(\omega_{res}\), y cómo se relaciona esto con su trama? (verificación de respuesta disponible en lightandmatter.com)
(c) ¿Cuál es la frecuencia resonante\(f_{res}\) correspondiente a su respuesta en la parte b? (consulta de respuesta disponible en lightandmatter.com)

45. A una frecuencia\(\omega\), cierto circuito LR serie tiene una impedancia de\(1\ \Omega+(2\ \Omega)i\). Supongamos que en cambio queremos lograr la misma impedancia usando dos elementos de circuito en paralelo. ¿Cuáles deben ser los elementos?

46. a) Utilizar la ley de Gauss para encontrar los campos dentro y fuera de una superficie cilíndrica infinita con radio\(b\) y densidad de carga superficial uniforme\(\sigma\). (verificación de respuesta disponible en lightandmatter.com)
(b) Mostrar que existe una discontinuidad en el campo eléctrico igual a\(4\pi k \sigma\) entre un lado de la superficie y el otro, como debería haber (ver página 628).
(c) Reexprese su resultado en términos del cargo por unidad de longitud, y compare con el campo de una línea de carga.
(d) Un cable coaxial tiene dos conductores: un conductor central de radio\(a\) y un conductor externo de radio\(b\). Estos dos conductores están separados por un aislante. Aunque dicho cable se usa normalmente para señales variables en el tiempo, supongamos a lo largo de este problema que simplemente hay una tensión de CC entre los dos conductores. El conductor externo es delgado, ya que en la parte c. El conductor interno es sólido, pero, como siempre ocurre con un conductor en electrostática, la carga se concentra en la superficie. Así, puedes encontrar todos los campos en la parte b superponiendo los campos debido a cada conductor, como se encuentra en la parte c. (Obsérvese que en una longitud dada del cable, la carga total de los conductores interno y externo es cero, así\(\lambda_1=-\lambda_2\), pero\(\sigma_1\ne\sigma_2\), ya que las áreas son desiguales). Encuentre la capacitancia por unidad de longitud de dicho cable. (consulta de respuesta disponible en lightandmatter.com)

47. En cierta región del espacio, el campo eléctrico es constante (es decir, el vector siempre tiene la misma magnitud y dirección). Por simplicidad, supongamos que el campo apunta en la\(x\) dirección positiva. a) Utilizar la ley de Gauss para probar que no hay ningún cargo en esta región del espacio. Esto se hace más fácilmente considerando una superficie gaussiana que consiste en una caja rectangular, cuyos bordes son paralelos a los\(z\) ejes\(x\)\(y\),, y.
b) Si no hay cargos en esta región del espacio, ¿qué podría estar haciendo este campo eléctrico?

48. (a) En un circuito LC en serie accionado por una tensión de CC (\(\omega=0\)), compare la energía almacenada en el inductor con la energía almacenada en el condensador.
(b) Realizar la misma comparación para un circuito LC que esté oscilando libremente (sin ningún voltaje de accionamiento).
(c) Consideremos ahora el caso general de un circuito LC en serie accionado por una tensión oscilante a una frecuencia arbitraria. Dejar\(\overline{U_L}\) y ser la energía promedio almacenada en el inductor, y de manera similar para\(\overline{U_C}\). Defina una cantidad\(u=\overline{U_C}/(\overline{U_L}+\overline{U_C})\), que puede interpretarse como la participación promedio del condensador en la energía, mientras que\(1-u\) es la participación promedio del inductor. Encuentra\(u\) en términos de\(L\),, y\(C\)\(\omega\), y bosquejar una gráfica de\(u\) y\(1-u\) versus\(\omega\). ¿Qué sucede en la resonancia? Asegúrese de que su resultado sea consistente con su respuesta a la parte a. (verificación de respuestas disponible en lightandmatter.com)

49. Usa la ley de Gauss para encontrar el campo dentro de un cilindro infinito con radio\(b\) y densidad de carga uniforme\(\rho\). (El campo externo tiene la misma forma que el del problema 46.) (consulta de respuesta disponible en lightandmatter.com)

50. (a) En cierta región del espacio, el campo eléctrico viene dado por\(\mathbf{E}=bx\hat{\mathbf{x}}\), donde\(b\) es una constante. Encuentra la cantidad de carga contenida dentro de un volumen cúbico que se extiende desde\(x=0\) hasta\(x=a\), desde\(y=0\) hasta\(y=a\), y desde\(z=0\) hasta\(z=a\).
b) Repetir para\(\mathbf{E}=bx\hat{\mathbf{z}}\).
(c) Repetir para\(\mathbf{E}=13bz\hat{\mathbf{z}}-7cz\hat{\mathbf{y}}\).
d) Repetir para\(\mathbf{E}=bxz\hat{\mathbf{z}}\).

51. La luz es una onda hecha de campos eléctricos y magnéticos, y los campos son perpendiculares a la dirección del movimiento de la onda, es decir, son transversales. Un ejemplo sería el campo eléctrico dado por\(\mathbf{E}=b \hat{\mathbf{x}} \sin cz\), donde\(b\) y\(c\) son constantes. (También habría un campo magnético asociado.) Observamos que la luz puede viajar a través de un vacío, por lo que esperamos que este patrón de ondas sea consistente con la inexistencia de alguna carga en el espacio que ocupa actualmente. Usa la ley de Gauss para probar que esto es cierto.

52. Este es un enfoque alternativo al problema 49, utilizando una técnica diferente. Supongamos que un cilindro largo contiene una densidad de carga uniforme\(\rho\) en todo su volumen interior.
a) Utilizar los métodos de la sección 10.7 para encontrar el campo eléctrico dentro del cilindro. (consulta de respuesta disponible en lightandmatter.com)
(b) Extiende tu solución a la región exterior, utilizando la misma técnica. Una vez que encuentre la forma general de la solución, ajústela para que los campos interior y exterior coincidan en la superficie. (consulta de respuesta disponible en lightandmatter.com)

53. El propósito de este problema de tarea es demostrar que la divergencia es invariante con respecto a las traducciones. Es decir, no importa dónde elijas poner el origen de tu sistema de coordenadas. Supongamos que tenemos un campo de la forma\(\mathbf{E}=ax\hat{\mathbf{x}}+by\hat{\mathbf{y}}+cz\hat{\mathbf{z}}\). Este es el campo más general que debemos considerar en cualquier región pequeña en lo que respecta a la divergencia. (La dependencia de\(x\),\(y\), y\(z\) es lineal, pero cualquier función suave parece lineal de cerca. Tampoco necesitamos poner en términos como\(x\hat{\mathbf{y}}\), porque no contribuyen a la divergencia.) Definir un nuevo conjunto de coordenadas\((u,v,w)\) relacionadas\((x,y,z)\) con

\[\begin{align*} x &= u + p \\ y &= v + q \\ z &= w + r , \end{align*}\]

donde\(p\),\(q\), y\(r\) son constantes. Demostrar que la divergencia del campo es la misma en estas nuevas coordenadas. Tenga en cuenta que\(\hat{\mathbf{x}}\) y\(\hat{\mathbf{u}}\) son idénticos, y de manera similar para las demás coordenadas.

54. Utilizando técnicas similares a la del problema 53, muestran que la divergencia es rotacionalmente invariable, en el caso especial de las rotaciones alrededor del\(z\) eje. En tal rotación, giramos a un nuevo sistema de\((u,v,z)\) coordenadas, cuyos ejes son girados un ángulo\(\theta \) con respecto a los del\((x,y,z)\) sistema. Las coordenadas están relacionadas por

\[\begin{align*} x &= u \cos \theta + v \sin \theta \\ y &= -u \sin \theta + v \cos \theta \end{align*}\]

Encuentra cómo\(\mathbf{E}\) dependen\(v\) los componentes\(u\) y el campo\(u\) y\(v\), y demuestra que su divergencia es la misma en este nuevo sistema de coordenadas.

55. Un campo eléctrico se da en coordenadas cilíndricas\((R,\phi,z)\) por\(E_R=ce^{-u|z|}R^{-1}\cos^2\phi\), donde la notación\(E_R\) indica el componente del campo apuntando directamente lejos del eje, y los componentes en las otras direcciones son cero. (Esta no es una expresión completamente imposible para el campo cerca de una antena transmisora de radio). (a) Encontrar la carga total encerrada dentro del cilindro infinitamente largo que se extiende desde el eje hacia fuera hasta\(R=b\). (b) Interpretar la\(R\) -dependencia de su respuesta a la parte a.

56. Utilice el teorema de Euler para derivar los teoremas de adición que expresan\(\sin(a+b)\) y\(\cos(a+b)\) en términos de los senos y cosenos de\(a\) y\(b\). (solución en la versión pdf del libro)

57. Encuentra cada número complejo\(z\) tal que\(z^3=1\). (solución en la versión pdf del libro)

58. Factorizar la expresión\(x^3-y^3\) en factores del orden más bajo posible, utilizando coeficientes complejos. (Pista: usa el resultado del problema 57.) Entonces haz lo mismo usando coeficientes reales. (solución en la versión pdf del libro)

Contributors and Attributions

Template:ContribCrowell