12.E: Electromagnetismo (Ejercicios)

1. Se observa una partícula con una carga de 1.0 C y una masa de 1.0 kg desplazándose más allá del punto P con una velocidad\((1.0\ \text{m}/\text{s})\hat{\mathbf{x}}\). El campo eléctrico en el punto P es\((1.0\ \text{V}/\text{m})\hat{\mathbf{y}}\), y el campo magnético es\((2.0\ \text{T})\hat{\mathbf{y}}\). Encuentra la fuerza que experimenta la partícula. (consulta de respuesta disponible en lightandmatter.com)

2. Para una partícula cargada positivamente que se mueve a través de un campo magnético, las direcciones de los\(\mathbf{F}\) vectores\(\mathbf{v}\)\(\mathbf{B}\), y están relacionadas por una regla de la derecha:

\[\begin{align*} \mathbf{v} & \text{along the fingers, with the hand flat}\\ \mathbf{B} & \text{along the fingers, with the knuckles bent}\\ \mathbf{F} & \text{along the thumb} \end{align*}\]

Hacer un modelo tridimensional de los tres vectores usando lápices o trozos de papel enrollados para representar los vectores ensamblados con sus colas juntas. Hacer los tres vectores perpendiculares entre sí. Ahora anote todas las formas posibles en las que la regla podría reescribirse cifrando los tres símbolos\(\mathbf{v}\),\(\mathbf{B}\), y\(\mathbf{F}\). En referencia a su modelo, ¿cuáles son correctos y cuáles son incorrectos?

3. Una partícula cargada se libera del resto. Vemos que empieza a moverse, y a medida que va, notamos que su trayectoria comienza a curvarse. ¿Podemos decir si esta región del espacio tiene\(\mathbf{E}\neq 0\), o\(\mathbf{B}\neq 0\), o ambas? Supongamos que no hay otras fuerzas presentes además de las posibles eléctricas y magnéticas, y que los campos, si están presentes, son uniformes.

4. Una partícula cargada se encuentra en una región del espacio en la que hay un campo magnético uniforme\(\mathbf{B}=B\hat{\mathbf{z}}\). No hay campo eléctrico, y ninguna otra fuerza actúa sobre la partícula. En cada caso, describa el movimiento futuro de la partícula, dada su velocidad inicial.

1. \(\mathbf{v}_\text{o}=0\)
2. \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{z}}\)
3. \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{y}}\)

5. (a) Una carga de línea, con carga por unidad de longitud\(\lambda\), se mueve a velocidad a\(v\) lo largo de su propia longitud. ¿Cuánto cargo pasa un determinado punto en el tiempo\(dt\)? ¿Cuál es la corriente resultante? \ hwans {hwans:linechargecurrent}
(b) Demuestra que las unidades de tu respuesta en parte a funcionan correctamente.

Esto constituye un modelo físico de una corriente eléctrica, y sería un modelo físicamente realista de un haz de partículas que se mueven en vacío, como el haz de electrones en un tubo de televisión. No es un modelo físicamente realista del movimiento de los electrones en un cable portador de corriente, o de los iones en su sistema nervioso; el movimiento de los portadores de carga en estos sistemas es mucho más complicado y caótico, y hay cargas de ambos signos, por lo que la carga total es cero. Pero incluso cuando el modelo es físicamente poco realista, sigue dando las respuestas correctas cuando lo usas para computar efectos magnéticos. Este es un hecho notable, que no vamos a probar. El lector interesado es referido a E.M. Purcell, Electricidad y Magnetismo, McGraw Hill, 1963.

6. Dos cables paralelos de longitud\(L\) llevan corrientes\(I_1\) y\(I_2\). Están separados por una distancia\(R\), y suponemos que\(R\) es mucho menor que\(L\), por lo que nuestros resultados para cables largos y rectos son precisos. El objetivo de este problema es calcular las fuerzas magnéticas que actúan entre los cables.
(a) Ninguno de los cables puede hacer una fuerza sobre sí mismo. Por lo tanto, nuestro primer paso para calcular la fuerza del cable 1 en el cable 2 es encontrar el campo magnético hecho solo por el cable 1, en el espacio ocupado por el cable 2. Exprese este campo en términos de las cantidades dadas. (answer check available at lightandmatter.com)
(b) Modelemos la corriente en el cable 2 pretendiendo que hay una carga de línea dentro de él, poseyendo densidad por unidad de longitud\(\lambda_2\) y moviéndose a velocidad\(v_2\). \(v_2\)Relacionar\(\lambda_2\) y con la corriente\(I_2\), usando el resultado del problema 5 a. ahora encuentre el cable de fuerza magnética 1 hace en el cable 2, en términos de\(I_1\)\(I_2\),\(L\), y\(R\). \ hwans {hwans:forcebetweentwowires}
(c) Mostrar que las unidades de la respuesta a la parte b funcionan para ser newtons.

7. Supongamos que una partícula cargada se mueve a través de una región del espacio en la que hay un campo eléctrico perpendicular a su vector de velocidad, y también un campo magnético perpendicular tanto al vector de velocidad de la partícula como al campo eléctrico. Demostrar que habrá una velocidad particular a la que se pueda mover la partícula que resulte en una fuerza total de cero sobre ella. Relacionar esta velocidad con las magnitudes de los campos eléctrico y magnético. (Tal disposición, llamada filtro de velocidad, es una forma de determinar la velocidad de una partícula desconocida).

8. Los siguientes datos dan los resultados de dos experimentos en los que se liberaron partículas cargadas desde el mismo punto en el espacio, y se midieron las fuerzas sobre ellas:

q 1 = 1 µ C	\(\mathbf{v}_1=(1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_1=(-1 mN)\mathbf{\hat y}\)
q 2 = - 2 µ C	\(\mathbf{v}_2=(-1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_2=(-2 mN)\mathbf{\hat y}\)

Los datos son insuficientes para determinar el vector de campo magnético; lo demuestran dando dos vectores de campo magnético diferentes, los cuales son consistentes con los datos.

9. Los siguientes datos dan los resultados de dos experimentos en los que se liberaron partículas cargadas desde el mismo punto en el espacio, y se midieron las fuerzas sobre ellas:

q 1 = 1 nC	\(\mathbf{v}_1=(1 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_1=(5 mN)\mathbf{\hat x}+(2 mN)\mathbf{\hat y}\)
q 2 = 1 nC	\(\mathbf{v}_2=(3 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_2=(10 mN)\mathbf{\hat x}+(4 mN)\mathbf{\hat y}\)

¿Hay un campo eléctrico distinto de cero en este punto? ¿Un campo magnético distinto de cero?

10. Este problema es una continuación del problema 6. Tenga en cuenta que la respuesta al problema 6 b se da en la página 930.

1. Intercambiando los 1's y 2's en la respuesta al problema 6 b, ¿cuál es la magnitud de la fuerza magnética del cable 2 que actúa sobre el cable 1? ¿Esto es consistente con la tercera ley de Newton?
2. Supongamos que las corrientes están en la misma dirección. Haga un boceto y use la regla de la derecha para determinar si el cable 1 tira del cable 2 hacia él o lo empuja hacia afuera.
3. Aplique nuevamente la regla de la derecha para encontrar la dirección de la fuerza del cable 2 en el cable 1. ¿Esto concuerda con la tercera ley de Newton?
4. ¿Qué pasaría si la corriente del cable 1 estuviera en la dirección opuesta en comparación con la del cable 2?

11. a) En la foto del aparato de tubo de vacío de la figura o de la página 656, inferir la dirección del campo magnético a partir del movimiento del haz de electrones. (La respuesta se da en la respuesta a la autocomprobación en esa página.)
(b) Con base en su respuesta a la parte a, encuentre la dirección de las corrientes en las bobinas.
(c) ¿En qué dirección van los electrones en las bobinas?
d) ¿Las corrientes en las bobinas repelen las corrientes que consisten en el haz dentro del tubo, o las atraen? Comprueba tu respuesta comparando con el resultado del problema 10.

12. Una partícula cargada de masa\(m\) y carga\(q\) se mueve en círculo debido a un campo magnético uniforme de magnitud\(B\), que apunta perpendicular al plano del círculo.

1. Supongamos que la partícula está cargada positivamente. Haga un boceto que muestre la dirección del movimiento y la dirección del campo, y muestre que la fuerza resultante está en la dirección correcta para producir movimiento circular.
2. Encuentra el radio,\(r\), del círculo, en términos de\(m\),\(q\),\(v\), y\(B\). (consulta de respuesta disponible en lightandmatter.com)
3. Demuestra que tu resultado de la parte b tiene las unidades adecuadas.
4. Discuta las cuatro variables que ocurren en el lado derecho de su respuesta de la parte b. ¿Tienen sentido? Por ejemplo, ¿qué debería pasar con el radio cuando el campo magnético se hace más fuerte? ¿Tu ecuación se comporta de esta manera?
5. Reformula tu resultado para que dé la frecuencia angular de la partícula,\(\omega\), en términos de las otras variables, y demuestre que\(v\) cae. (consulta de respuesta disponible en lightandmatter.com)

Una partícula cargada puede acelerarse en un dispositivo circular llamado ciclotrón, en el que un campo magnético es lo que les impide salir rectos. Por lo tanto, esta frecuencia se conoce como la frecuencia de ciclotrón. Las partículas son aceleradas por otras fuerzas (fuerzas eléctricas), que son AC. Siempre y cuando el campo eléctrico se opere a la frecuencia de ciclotrón correcta para el tipo de partículas que se manipulan, se mantendrá sincronizado con las partículas, dándoles un empujón en la dirección correcta cada vez que pasen. Las partículas se están acelerando, por lo que esto sólo funciona porque la frecuencia del ciclotrón es independiente de la velocidad.

a/Problema 13.

13. Cada figura representa el movimiento de una partícula cargada positivamente. Los puntos dan las posiciones de las partículas a intervalos de tiempo iguales. En cada caso, determine si el movimiento fue causado por una fuerza eléctrica, una fuerza magnética o una fuerza de fricción, y explique su razonamiento. Si es posible, determinar la dirección del campo magnético o eléctrico. Todos los campos son uniformes. En (a), la partícula se detiene por un instante en la parte superior derecha, pero luego vuelve hacia abajo y hacia la izquierda, retrocediendo los mismos puntos. En la (b), se detiene en la parte superior derecha y permanece ahí.

14. Un modelo del átomo de hidrógeno tiene el electrón dando vueltas alrededor del protón a una velocidad de\(2.2\times10^6\) m/s, en una órbita con un radio de 0.05 nm. (Aunque el electrón y el protón realmente orbitan alrededor de su centro de masa común, el centro de masa está muy cerca del protón, ya que es 2000 veces más masivo. Para este problema, supongamos que el protón es estacionario.)

1. Trate el electrón circulante como un bucle de corriente y calcule la corriente.
2. Estimar el campo magnético creado en el centro del átomo por el electrón. (consulta de respuesta disponible en lightandmatter.com)
3. ¿El protón experimenta una fuerza distinta de cero del campo magnético del electrón? Explique.
4. ¿El electrón experimenta un campo magnético del protón? Explique.
5. ¿El electrón experimenta un campo magnético creado por su propia corriente? Explique.
6. ¿Existe una fuerza eléctrica que actúe entre el protón y el electrón? Si es así, calcule. (consulta de respuesta disponible en lightandmatter.com)
7. ¿Existe una fuerza gravitacional que actúe entre el protón y el electrón? Si es así, calcule.
8. Se requiere una fuerza interna para mantener al electrón en su órbita —de lo contrario obedecería la primera ley de Newton e iría recto, dejando el átomo. Con base en sus respuestas a las partes anteriores, ¿qué fuerza o fuerzas (eléctricas, magnéticas y gravitacionales) contribuyen significativamente a esta fuerza interior? (Basado en un problema de Arnold Arons.)

15. La ecuación\(B_z=\beta kIA/c^2r^3\) se encontró en la página 666 para el campo distante de un dipolo. Demostrar, como ahí se afirma, que la constante\(\beta\) debe ser sin unidades.

16. Los siguientes datos dan los resultados de tres experimentos en los que se liberaron partículas cargadas desde el mismo punto en el espacio, y se midieron las fuerzas sobre ellas:

q 1 = 1 C	\(\mathbf{v}_1=0\)	\(\mathbf{F}_1=(1 N)\mathbf{\hat y}\)
q 2 = 1 C	\(\mathbf{v}_2=(1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_2=(1 N)\mathbf{\hat y}\)
q 3 = 1 C	\(\mathbf{v}_3=(1 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_3=0\)

Determinar los campos eléctricos y magnéticos. (consulta de respuesta disponible en lightandmatter.com)

17. Si pones cuatro veces más corriente a través de un solenoide, ¿cuántas veces más energía se almacena en su campo magnético? (consulta de respuesta disponible en lightandmatter.com)

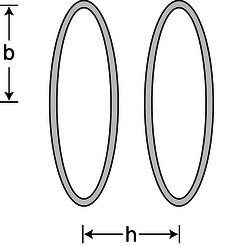
b/Problema 18.

18. Una bobina de Helmholtz se define como un par de bobinas circulares idénticas que se encuentran en planos paralelos y separadas por una distancia\(h\),, igual a su radio,\(b\). (Cada bobina puede tener más de una vuelta de cable). La corriente circula en la misma dirección en cada bobina, por lo que los campos tienden a reforzarse entre sí en la región interior. Esta configuración tiene la ventaja de ser bastante abierta, de manera que otros aparatos pueden colocarse fácilmente dentro y someterse al campo mientras permanecen visibles desde el exterior. La elección de\(h=b\) resultados en el campo más uniforme posible cerca del centro. Una fotografía de una bobina de Helmholtz fue mostrada en la figura o en la página 656.
(a) Encontrar el porcentaje de caída en el campo en el centro de una bobina, en comparación con la fuerza total en el centro de todo el aparato. (verificación de respuesta disponible en lightandmatter.com)
(b) ¿Qué valor de\(h\) (no igual a\(b)\) haría que esta diferencia porcentual sea igual a cero? (consulta de respuesta disponible en lightandmatter.com)

c/Problema 19.

19. La figura muestra un par anidado de bucles de alambre circulares utilizados para crear campos magnéticos. (La torsión de los cables es un truco práctico para reducir los campos magnéticos que aportan, por lo que los campos están muy cerca de lo que esperaríamos para un bucle de corriente circular ideal). El sistema de coordenadas a continuación es para facilitar la discusión de las direcciones en el espacio. Un bucle está en el\(y-z\) plano, el otro en el\(x-y\) plano. Cada uno de los bucles tiene un radio de 1.0 cm, y lleva 1.0 A en la dirección indicada por la flecha.

1. Calcular el campo magnético que produciría uno de esos bucles, en su centro. (consulta de respuesta disponible en lightandmatter.com)
2. Describir la dirección del campo magnético que sería producido, en su centro, por el bucle solo en el\(x-y\) plano.
3. Haz lo mismo para el otro bucle.
4. Calcular la magnitud del campo magnético producido por los dos bucles en combinación, en su centro común. Describir su dirección. (consulta de respuesta disponible en lightandmatter.com)

d/Problema 20.

20. Cuatro cables largos están dispuestos, como se muestra, de manera que su sección transversal forme un cuadrado, con conexiones en los extremos para que la corriente fluya a través de los cuatro antes de salir. Tenga en cuenta que la corriente está a la derecha en los dos cables posteriores, pero a la izquierda en los cables frontales. Si las dimensiones del cuadrado transversal (altura y adelante hacia atrás) son\(b\), encuentre el campo magnético (magnitud y dirección) a lo largo del eje central largo. (consulta de respuesta disponible en lightandmatter.com)

21. En el problema 16, los tres experimentos dieron suficiente información para determinar ambos campos. ¿Es posible diseñar un procedimiento para que, utilizando sólo dos de esos experimentos, siempre podamos encontrar\(\mathbf{E}\) y\(\mathbf{B}\)? Si es así, diseñarlo. Si no, ¿por qué no?

22. Utilice la ley Biot-Savart para derivar el campo magnético de un cable largo y recto, y mostrar que éste reproduce el resultado del ejemplo 6 de la página 658.

23. a) Modificar el cálculo de la página 663 para determinar el componente del campo magnético de una hoja de carga que es perpendicular a la hoja. (consulta de respuesta disponible en lightandmatter.com)
(b) Demuestra que tu respuesta tiene las unidades adecuadas.
(c) Demuestre que su respuesta se aproxima al cero a medida que\(z\) se acerca
d) ¿Qué sucede con su respuesta en el caso de\(a=b\)? Explique por qué esto tiene sentido.

24. Considera dos solenoides, uno de los cuales es más pequeño para que se pueda poner dentro del otro. Supongamos que son lo suficientemente largos para que cada uno solo contribuya significativamente al campo dentro de sí mismo, y los campos interiores son casi uniformes. Considera la configuración donde está la pequeña dentro de la grande con sus corrientes circulando en la misma dirección, y una segunda configuración en la que las corrientes circulan en direcciones opuestas. Compara las energías de estas configuraciones con la energía cuando los solenoides están muy separados. En base a este razonamiento, ¿qué configuración es estable y en qué configuración tenderá el pequeño solenoide a retorcerse o escupirá? \ hwhint {hwhint:solenoides anidados}

e/Problema 25.

25. (a) Un solenoide puede imaginarse como una serie de bucles de corriente circulares que están espaciados a lo largo de su eje común. Integrar el resultado del ejemplo 12 en la página 671 para mostrar que el campo en el eje de un solenoide puede escribirse como\(B=(2\pi k\eta/c^2)(\cos\beta+\cos\gamma)\), donde los ángulos\(\beta\) y se\(\gamma\) definen en la figura.
(b) Demostrar que en el límite donde el solenoide es muy largo, este resultado exacto concuerda con el aproximado derivado en el ejemplo 13 de la página 674 utilizando la ley de Ampère.
c) Obsérvese que, a diferencia del cálculo que utiliza la ley de Ampère, éste es válido en puntos que están cerca de las bocas del solenoide, o incluso fuera de él completamente. Si el solenoide es largo, ¿en qué punto del eje el campo es igual a la mitad de su valor en el centro del solenoide?
(d) ¿Qué sucede con tu resultado cuando lo aplicas a puntos que están muy alejados del solenoide? ¿Tiene sentido esto?

26. El primer paso en la prueba de la ley de Ampère en la página 675 es mostrar que la ley de Ampère sostiene en el caso que se muestra en la figura f /1, donde un bucle Ampèrian circular se centra en un alambre largo y recto que es perpendicular al plano del bucle. Realizar este cálculo, utilizando el resultado para el campo de un cable que se estableció sin utilizar la ley de Ampère.

27. Una cierta región del espacio tiene un campo magnético dado por\(\mathbf{B}=bx\hat{\mathbf{y}}\). Encuentra la corriente eléctrica que fluye a través del cuadrado definido por\(z=0\),\(0\le x \le a\), y\(0\le y \le a\). (consulta de respuesta disponible en lightandmatter.com)

f/Un caparazón nautilus es aproximadamente una espiral logarítmica, del tipo del problema 28.

28. Realizar un cálculo similar al del problema 54, pero para una espiral logarítmica, definida por\(r=we^{u\theta}\), y mostrar que el campo es\(B=(kI/c^2u)(1/a-1/b)\). Tenga en cuenta que la solución al problema 54 se da en la parte posterior del libro.

29. (a) Para la geometría descrita en el ejemplo 8 de la página 661, busque el campo en un punto las mentiras en el plano de los cables, pero no entre los cables, a una\(b\) distancia de la línea central. Usa la misma técnica que en ese ejemplo.
(b) Ahora rehacer el cálculo utilizando la técnica demostrada en la página 666. Las integrales son casi las mismas, pero ahora se invierte el razonamiento: ya lo sabes\(\beta=1\), y quieres encontrar un campo desconocido. La única diferencia en las integrales es que estás alicatando una región diferente del plano para simular las corrientes en los dos cables. Tenga en cuenta que no se puede colocar en mosaico una región que contenga un punto de interés, ya que la técnica utiliza el campo de un dipolo distante. (consulta de respuesta disponible en lightandmatter.com)

30. (a) Un solenoide largo y delgado consiste en\(N\) vueltas de alambre enrolladas uniformemente alrededor de un cilindro hueco de longitud\(\ell\) y área de sección transversal\(A\). Encuentra su inductancia. (consulta de respuesta disponible en lightandmatter.com)
(b) Demuestra que tu respuesta tiene las unidades adecuadas para ser una inductancia.

31. Considera dos solenoides, uno de los cuales es más pequeño para que se pueda poner dentro del otro. Supongamos que son lo suficientemente largos como para actuar como solenoides ideales, de modo que cada uno solo contribuye significativamente al campo dentro de sí mismo, y los campos interiores son casi uniformes. Considera la configuración donde el pequeño está parcialmente dentro y en parte colgando de la grande, con sus corrientes circulando en la misma dirección. Sus ejes están restringidos para que coincidan.
(a) Encontrar la diferencia en la energía magnética entre la configuración donde los solenoides están separados y la configuración donde el pequeño se inserta en el grande. Su ecuación incluirá la longitud\(x\) de la parte del solenoide pequeño que se encuentra dentro del gran, así como otras variables relevantes que describen los dos solenoides. (verificación de respuesta disponible en lightandmatter.com)
(b) Basado en su respuesta a la parte a, encuentre la fuerza que actúa entre los solenoides. (consulta de respuesta disponible en lightandmatter.com)

g/Problema 32.

32. Verificar la ley de Ampère en el caso mostrado en la figura, asumiendo la ecuación conocida para el campo de un cable. Un alambre que transporta corriente\(I\) pasa perpendicularmente a través del centro de la superficie rectangular Ampèrian. La longitud del rectángulo es infinita, por lo que no es necesario calcular las contribuciones de los extremos.

33. El propósito de este problema es encontrar cómo la ganancia de un transformador depende de su construcción.
(a) Se cambia el número de bucles de cable\(N\),, en un solenoide, manteniendo constante la longitud. ¿De qué depende la impedancia\(N\)? Exponga su respuesta como una proporcionalidad, e.g.,\(Z\propto N^3\) o\(Z\propto N^{-5}\).
(b) Para un voltaje de CA dado aplicado a través del inductor, ¿de qué depende el campo magnético\(N\)? Es necesario tener en cuenta tanto la dependencia del campo de un solenoide\(N\) para una corriente determinada como su respuesta a la parte a, que afecta a la corriente.
(c) Consideremos ahora un transformador que consta de dos solenoides. El lado de entrada tiene\(N_1\) bucles, y la salida\(N_2\). Deseamos encontrar cómo\(V_2\) depende el voltaje de salida de\(N_1\),\(N_2\), y el voltaje de entrada\(V_1\). El texto ya lo ha establecido\(V_2\propto V_1N_2\), por lo que sólo queda por encontrar la dependencia de\(N_1\). Utilice su resultado de la parte b para lograr esto. La relación\(V_2/V_1\) se llama ganancia de voltaje.

34. El problema 33 se refería a la dependencia de la ganancia de un transformador en el número de bucles de cable en el solenoide de entrada. Realizar un análisis similar de cómo la ganancia depende de la frecuencia a la que se opera el circuito.

h/Problema 35.

35. Un cable en forma de U hace contacto eléctrico con un segundo cable recto, que rueda a lo largo de él hacia la derecha, como se muestra en la figura. Todo está inmerso en un campo magnético uniforme, que es perpendicular al plano del circuito. La resistencia del alambre rodante es mucho mayor que la de la U.
(a) Encuentra la dirección de la fuerza sobre el alambre en base a la conservación de energía.
b) Verificar la dirección de la fuerza utilizando reglas de la derecha.
(c) Encontrar la magnitud de la fuerza que actúa sobre el cable. Hay más de una manera de hacerlo, pero por favor hágalo usando la ley de Faraday (que funciona a pesar de que es la propia superficie ampèriana la que está cambiando, más que el campo). (verificación de respuesta disponible en lightandmatter.com)
(d) Considere cómo habría cambiado la respuesta a la parte a si se hubiera invertido la dirección del campo, y también haga el caso donde se invierte la dirección del movimiento del alambre rodante. Verifica que esto esté de acuerdo con tu respuesta a la parte c.

36. Una partícula cargada está en movimiento a velocidad\(v\), en una región de vacío a través de la cual pasa una onda electromagnética. ¿En qué dirección debe moverse la partícula para minimizar la fuerza total que actúa sobre ella? Considera ambas posibilidades para la señal de la carga. (Basado en un problema de David J. Raymond.)

i/Problema 37.

37. Un bucle de alambre de resistencia\(R\) y área\(A\), tendido en el\(y-z\) plano, cae a través de un campo magnético no uniforme\(\mathbf{B}=kz\hat{\mathbf{x}}\), donde\(k\) es una constante. El\(z\) eje es vertical.
(a) Encontrar la dirección de la fuerza sobre el alambre en función de la conservación de energía.
b) Verificar la dirección de la fuerza utilizando reglas de la derecha.
(c) Encontrar la fuerza magnética en el cable. (consulta de respuesta disponible en lightandmatter.com)

38. Un condensador tiene placas paralelas de área\(A\), separadas por una distancia\(h\). Si hay un vacío entre las placas, entonces la ley de Gauss da\(E=4\pi k\sigma=4\pi kq/A\) para el campo entre las placas, y combinando esto con\(E=V/h\), nos encontramos\(C=q/V=(1/4\pi k)A/h\). (a) Generalizar esta derivación al caso en que exista un dieléctrico entre las placas. (b) Supongamos que tenemos una lista de materiales posibles que podríamos elegir como dieléctricos, y deseamos construir un condensador que tenga la mayor densidad de energía posible,\(U_e/v\), donde\(v\) está el volumen. Para cada dieléctrico, conocemos su permitividad\(\epsilon\), y también el campo eléctrico máximo\(E\) que puede sostener sin romperse y permitiendo que las chispas crucen entre las placas. Escribir la densidad máxima de energía en términos de estas dos variables, y determinar una cifra de mérito que podría ser utilizada para decidir qué material sería la mejor opción.

39. (a) Por cada término que aparece en el lado derecho de las ecuaciones de Maxwell, dar un ejemplo de una situación cotidiana que describe.
(b) La mayoría de las personas que hacen cálculos en el sistema SI de unidades no utilizan\(k\) y\(k/c^2\). En cambio, expresan todo en términos de las constantes

\[\begin{align*} \epsilon_\text{o}&=\frac{1}{4\pi k} \text{and} \\ \mu_\text{o}&=\frac{4\pi k}{c^2} . \end{align*}\]

Reescribe las ecuaciones de Maxwell en términos de estas constantes, eliminando\(k\) y\(c\) en todas partes.

40. a) Demostrar que en una onda plana electromagnética, la mitad de la energía está en el campo eléctrico y la mitad en el campo magnético.
(b) Con base en su resultado de la parte a, encuentre la constante de proporcionalidad en la relación\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}dv\), donde\(d \mathbf{p}\) está el impulso de la parte de una onda de luz plana contenida en el volumen\(dv\). El vector\(\mathbf{E}\times\mathbf{B}\) se conoce como el vector Poynting. (Para hacer este problema, es necesario conocer la relación relativista entre la energía y el impulso de un haz de luz.) (consulta de respuesta disponible en lightandmatter.com)

41. (a) Un haz de luz tiene área de sección transversal\(A\) y potencia\(P\), es decir,\(P\) es el número de julios por segundo que entran en una ventana por la que pasa el haz. Encuentra la densidad energética\(U/v\) en términos de\(P\)\(A\), y constantes universales.
(b) Encontrar\(\tilde{\mathbf{E}}\) y\(\tilde{\mathbf{B}}\), las amplitudes de los campos eléctricos y magnéticos, en términos de\(P\)\(A\), y constantes universales (es decir, su respuesta no debe incluir\(U\) o\(v\)). Necesitarás el resultado del problema 40 a. un haz de luz real generalmente consiste en muchos trenes de onda cortos, no una onda sinusoidal grande, pero no te preocupes por eso. (answer check available at lightandmatter.com)\ hwhint {hwhint:solarconstant}
(c) Un haz de luz solar tiene una intensidad de\(P/A=1.35\times10^3\ \text{W}/\text{m}^2\), asumiendo que no hay nubes ni absorción atmosférica. A esto se le conoce como la constante solar. Calcula\(\tilde{\mathbf{E}}\) y\(\tilde{\mathbf{B}}\), y compara con las fortalezas de los campos estáticos que experimentas en la vida cotidiana:\(E \sim 10^6\ \text{V}/\text{m}\) en una tormenta eléctrica, y\(B \sim 10^{-3}\) T para el campo magnético de la Tierra. (consulta de respuesta disponible en lightandmatter.com)

j/Problema 42.

42. El condensador circular de placa paralela que se muestra en la figura se está cargando con el tiempo, variando la diferencia de voltaje a través de las placas como\(V=st\), donde\(s\) es una constante. Las placas tienen radio\(b\), y la distancia entre ellas es\(d\). Suponemos\(d \ll b\), de manera que el campo eléctrico entre las placas es uniforme, y paralelo al eje. Encuentra el campo magnético inducido en un punto entre las placas, a una\(R\) distancia del eje. \ hwhint {hwhint:circularcap} (consulta de respuesta disponible en lightandmatter.com)

43. Una partícula cargada positivamente se libera del reposo en el origen en\(t=0\), en una región de vacío a través de la cual pasa una onda electromagnética. La partícula se acelera en respuesta a la ola. En esta región del espacio, la onda varía como\(\mathbf{E}=\hat{\mathbf{x}}\tilde{E}\sin\omega t\),\(\mathbf{B}=\hat{\mathbf{y}}\tilde{B}\sin\omega t\), y suponemos que la partícula tiene un valor relativamente grande de\(m/q\), por lo que su respuesta a la onda es lenta, y nunca termina moviéndose a ninguna velocidad comparable a la velocidad de la luz. Por lo tanto, no tenemos que preocuparnos por la variación espacial de la ola; solo podemos imaginar que se trata de campos uniformes impuestos por algún mecanismo externo sobre esta región del espacio.
(a) Encontrar las coordenadas de la partícula como función del tiempo. (cheque de respuesta disponible en lightandmatter.com)
(b) Demostrar que la moción se limita a\(-z_{max}\leq z \leq z_{max}\), donde\(z_{max} = 1.101\left(q^2\tilde{E}\tilde{B}/m^2\omega^3\right)\).

44. Se supone que las ondas electromagnéticas tienen sus campos eléctricos y magnéticos perpendiculares entre sí. (A lo largo de este problema, supongamos que estamos hablando de ondas que viajan a través de un vacío, y que solo hay una sola onda sinusoidal viajando en una sola dirección, no una superposición de ondas sinusoidales que pasan entre sí). Supongamos que alguien afirma que puede hacer una onda electromagnética en la que los campos eléctrico y magnético se encuentran en el mismo plano. Demostrar que esto es imposible con base en las ecuaciones de Maxwell.

45. Repita la autocomprobación en la página 710, pero con un cambio en el procedimiento: después de cargar el condensador, abrimos el circuito, y luego continuamos con las observaciones.

46. En la página 713, probé que\(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\) en el límite entre dos sustancias si no hay corriente libre y los campos son estáticos. De hecho, cada una de las cuatro ecuaciones de Maxwell implica una restricción con una estructura similar. Algunas son restricciones en los componentes de campo paralelas al límite, mientras que otras son restricciones en las partes perpendiculares. Ya que algunos de los campos a los que se hace referencia en las ecuaciones de Maxwell son los campos eléctricos\(\mathbf{E}\) y magnéticos y\(\mathbf{B}\), mientras que otros son los campos auxiliares\(\mathbf{D}\) y\(\mathbf{H}\), algunas de las restricciones tratan\(\mathbf{E}\) y\(\mathbf{B}\), otros con\(\mathbf{D}\) y\(\mathbf{H}\). Encuentra las otras tres restricciones.

47. (a) La figura j de la página 714 muestra una esfera hueca con\(\mu/\mu_\text{o}=x\) radio\(a\) interior y radio exterior\(b\), la cual ha sido sometida a un campo externo\(\mathbf{B}_\text{o}\). Encontrar los campos en el exterior, en el caparazón y en el interior requiere encontrar un conjunto de campos que satisfagan cinco condiciones de límite: (1) lejos de la esfera, el campo debe acercarse a la constante\(\mathbf{B}_\text{o}\); (2) en la superficie exterior de la esfera, el campo debe tener\(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\), como se discute en la página 713; (3) la misma restricción se aplica en la superficie interna de la esfera; (4) y (5) existe una restricción adicional en los campos en las superficies interna y externa, como se encuentra en el problema 46. El objetivo de este problema es encontrar la solución para los campos, y a partir de ella, demostrar que el campo interior es uniforme, y dado por

\[\begin{equation*} \mathbf{B} = \left[\frac{9x}{(2x+1)(x+2)-2\frac{a^3}{b^3}(x-1)^2}\right]\mathbf{B}_\text{o} . \end{equation*}\]

Este es un problema muy difícil de resolver desde los primeros principios, porque no es obvio qué forma deberían tener los campos, y si no te hubieran dicho, probablemente no habrías adivinado que el campo interior sería uniforme. Podríamos, sin embargo, adivinar que una vez que la esfera se polariza por el campo externo, se convertiría en un dipolo\(r\gg b\), y en, el campo sería un campo uniforme superpuesto sobre el campo de un dipolo. Resulta que incluso cerca de la esfera, la solución tiene exactamente esta forma. Para completar la solución, necesitamos encontrar el campo en la concha (\(a\lt r\lt b\)), pero la única forma en que este campo podría coincidir con la variación angular detallada de los campos interior y exterior sería si también se tratara de una superposición de un campo uniforme con un campo dipolar. El resultado final es que tenemos cuatro incógnitas: la fuerza del componente dipolo del campo externo, la fuerza de los componentes uniforme y dipolo del campo dentro de la concha, y la fuerza del campo interior uniforme. Estas cuatro incógnitas se determinarán imponiendo las restricciones (2) a (5) anteriores.
(b) Demostrar que la expresión de la parte a tiene un comportamiento físicamente razonable en su dependencia de\(x\) y\(a/b\).

48. Dos tiras largas y paralelas de lámina metálica delgada forman una configuración como un sándwich largo y estrecho. El entrehierro entre ellos tiene altura\(h\), el ancho de cada tira es\(w\), y su longitud es\(\ell\). Cada tira lleva corriente\(I\), y asumimos por concreción que las corrientes están en direcciones opuestas, de manera que la fuerza magnética,\(F\), entre las tiras es repulsiva.
a) Encontrar la fuerza en el límite de\(w\gg h\). (verificación de respuesta disponible en lightandmatter.com)
(b) Encuentra la fuerza en el límite de\(w\ll h\), que es como dos cables ordinarios.
(c) Discutir la relación entre los dos resultados.

49. Supongamos que se nos da un imán permanente con una forma complicada y asimétrica. Describir cómo una serie de mediciones con brújula magnética podrían ser utilizadas para determinar la intensidad y dirección de su campo magnético en algún punto de interés. Suponga que solo puede ver la dirección en la que se asienta la aguja de la brújula; no puede medir el par que actúa sobre ella.

50. En la página 680, se\(x\hat{\mathbf{y}}\) computó el rizo de. Ahora considere los campos\(x\hat{\mathbf{x}}\) y\(y\hat{\mathbf{y}}\).
a) Esbozar estos campos.
(b) Utilizando la misma técnica de construir explícitamente un pequeño cuadrado, demostrar que sus rizos son ambos cero. No utilice la forma componente del rizo; esto fue un paso para derivar la forma componente del rizo.

51. Si ves una película reproducida al revés, algunos vectores invierten su dirección. Por ejemplo, la gente camina hacia atrás, con sus vectores de velocidad volteados. Otros vectores, como las fuerzas, mantienen la misma dirección, por ejemplo, la gravedad aún tira hacia abajo. Un campo eléctrico es otro ejemplo de un vector que no da la vuelta: las cargas positivas siguen siendo positivas en el universo de tiempo invertido, por lo que todavía hacen campos eléctricos divergentes, y de igual manera para los campos convergentes alrededor de cargas negativas.
a) ¿Cómo se comporta el impulso de un objeto material bajo la inversión del tiempo? (solución en la versión pdf del libro)
(b) Las leyes de la física siguen siendo válidas en el universo invertido en el tiempo. Por ejemplo, mostrar que si dos objetos materiales están interactuando, y se conserva el impulso, entonces el impulso aún se conserva en el universo invertido en el tiempo. (solución en la versión pdf del libro)
(c) Discutir cómo se comportarían las corrientes y los campos magnéticos bajo la inversión del tiempo. \ hwhint {hwhint:timereversalem}
(d) Del mismo modo, mostrar que la ecuación\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) sigue siendo válida bajo inversión de tiempo.

52. Este problema es una exploración más avanzada de las ideas de inversión temporal introducidas en el problema 51.
(a) En ese problema, asumimos que la carga no volteaba su signo bajo inversión de tiempo. Supongamos que hacemos la suposición opuesta, ese cargo sí cambia su signo. Esta es una idea introducida por Richard Feynman: ¡esa antimateria es realmente materia viajando hacia atrás en el tiempo! Determine las propiedades de inversión de tiempo de\(\mathbf{E}\) y\(\mathbf{B}\) bajo este nuevo supuesto, y demuestre que\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) sigue siendo válido bajo inversión de tiempo.
(b) Demostrar que las ecuaciones de Maxwell son simétricas de inversión de tiempo, es decir, que si los campos\(\mathbf{E}(x,y,z,t)\) y\(\mathbf{B}(x,y,z,t)\) satisfacen las ecuaciones de Maxwell, entonces así lo hacen\(\mathbf{E}(x,y,z,-t)\) y\(\mathbf{B}(x,y,z,-t)\). Demostrar esto bajo ambos supuestos posibles sobre la carga,\(q\rightarrow q\) y\(q\rightarrow -q\).

53. El propósito de este problema es demostrar que la constante de proporcionalidad\(a\) en la ecuación\(dU_m=aB^2 dv\), para la densidad energética del campo magnético, viene dada por\(a=c^2/8\pi k\) como se afirma en la página 665. La geometría que usaremos consiste en dos láminas de corriente, como un sándwich sin nada en el medio sino algo de vacío en el que hay un campo magnético. Las corrientes están en direcciones opuestas, y podemos imaginarlas como unidas en los extremos para formar un circuito completo, como un tubo hecho de papel que ha sido aplastado casi plano. Las hojas tienen longitudes\(L\) en la dirección paralela a la corriente, y anchuras\(w\). Están separados por una distancia\(d\), que, por conveniencia, suponemos que es pequeña en comparación con\(L\) y\(w\). Así, la contribución de cada hoja al campo es uniforme, y puede ser aproximada por la expresión\(2\pi k\eta/c^2\).
a) Hacer un dibujo similar al de la figura 11.2.1 de la página 664, y mostrar que en esta configuración de corriente opuesta, los campos magnéticos de las dos hojas se refuerzan en la región entre ellas, produciendo el doble de campo, pero cancelando en el exterior.
(b) Por analogía con el caso de un solo hilo de alambre, la fuerza de una hoja sobre la otra es\(ILB_1\), eran\(I=\eta w\) es la corriente total en una hoja, y\(B_1=B/2\) es el campo aportado por solo una de las láminas, ya que la lámina no puede hacer ninguna fuerza neta sobre sí misma. Con base en tu dibujo y en la regla de la derecha, demuestra que esta fuerza es repulsiva.
Para el resto del problema, considere un proceso en el que las hojas comiencen a tocarse, y luego se separen a cierta distancia\(d\). Dado que la fuerza entre las láminas es repulsiva, hacen trabajo mecánico en el mundo exterior a medida que se separan, de la misma manera que el pistón en un motor sí funciona a medida que los gases dentro del cilindro se expanden. Al mismo tiempo, sin embargo, existe una emf inducida que tendería a extinguir la corriente, por lo que para mantener una corriente constante, se tendrá que drenar la energía de una batería. Hay tres tipos de energía involucrados: el aumento de la energía del campo magnético, el aumento de la energía del mundo exterior y la disminución de la energía a medida que se agota la batería. (Suponemos que las láminas tienen muy poca resistencia, por lo que no hay calentamiento óhmico involucrado.) (consulta de respuesta disponible en lightandmatter.com)
(c) Encuentra el trabajo mecánico realizado por las hojas, lo que equivale al incremento de la energía del mundo exterior. Demuestre que su resultado puede ser expresado en términos de\(\eta\), el volumen final\(v=wLd\), y nada más que constantes numéricas y físicas. (verificación de respuesta disponible en lightandmatter.com)
(d) La potencia suministrada por la batería es\(P=I\Gamma_E\) (como\(P=I\Delta V\), pero con una emf en lugar de una diferencia de voltaje), y la circulación viene dada por\(\Gamma=-d\Phi_B/dt\). El signo negativo indica que se está agotando la batería. Calcular la energía suministrada por la batería, y, como en la parte c, mostrar que el resultado puede ser expresado en términos de\(\eta\)\(v\), y constantes universales. (verificación de respuesta disponible en lightandmatter.com)
(e) Encontrar el incremento en la energía del campo magnético, en términos de\(\eta\)\(v\), y la constante desconocida\(a\). (cheque de respuesta disponible en lightandmatter.com)
(f) Usa la conservación de energía para relacionar tus respuestas de las partes c, d y e, y resolver para\(a\). (consulta de respuesta disponible en lightandmatter.com)

k/Problema 54.

54. Las bobinas magnéticas a menudo están envueltas en múltiples capas. La figura muestra el caso especial donde todas las capas están confinadas a un solo plano, formando una espiral. Dado que el grosor de los alambres (más su aislamiento) es fijo, la espiral que resulta es un tipo matemático conocido como espiral de Arquímedes, en la que las vueltas están espaciadas uniformemente. La ecuación de la espiral es\(r=w\theta\), donde\(w\) es una constante. Para una espiral que comienza desde\(r=a\) y termina en\(r=b\), mostrar que el campo en el centro viene dado por\((kI/c^2w)\ln b/a\). (solución en la versión pdf del libro)

Contributors and Attributions

Template:ContribCrowell