13.2: Imágenes por reflexión

Los infantes siempre están fascinados por las payasadas del Bebé en el Espejo. Ahora bien, si quieres saber algo sobre las imágenes espejo que la mayoría de la gente no entiende, prueba esto. Primero acerque esta página cada vez más a tus ojos, hasta que ya no puedas enfocarte en ella sin esforzarte. Entonces ve al baño y ve lo cerca que puedes acercar tu cara a la superficie del espejo antes de que ya no puedas enfocarte fácilmente en la imagen de tus propios ojos. Encontrará que la distancia cómoda más corta del espejo del ojo es mucho menor que la distancia cómoda más corta del ojo-papel. Esto demuestra que la imagen de tu rostro en el espejo actúa como si tuviera profundidad y existiera en el espacio detrás del espejo. Si la imagen fuera como una imagen plana en un libro, entonces no podrías enfocarte en ella desde tan corta distancia.

En este capítulo estudiaremos las imágenes formadas por espejos planos y curvos sobre una base cualitativa, conceptual. Si bien este tipo de imagen no se encuentra tan comúnmente en la vida cotidiana como las imágenes formadas por lentes, las imágenes formadas por la reflexión son más sencillas de entender, por lo que las discutimos primero. En la sección 12.3 pasaremos a un tratamiento más matemático de las imágenes hechas por reflexión. Sorprendentemente, las mismas ecuaciones también se pueden aplicar a las lentes, que son el tema de la sección 12.4.

12.2.1 Una imagen virtual

a/Una imagen formada por un espejo.

Podemos entender una imagen especular usando un diagrama de rayos. La figura a muestra varios rayos de luz, 1, que se originaron por reflexión difusa en la nariz de la persona. Rebotan en el espejo, produciendo nuevos rayos, 2. A cualquiera cuyo ojo esté en la posición correcta para obtener uno de estos rayos, parecen haber venido de un detrás del espejo, 3, donde se habrían originado a partir de un solo punto. Este punto es donde parece estar la punta de la nariz de la persona imagen-persona. Un análisis similar se aplica a cualquier otro punto del rostro de la persona, por lo que parece como si hubiera una cara entera detrás del espejo. La forma habitual de describir la situación requiere alguna explicación:

• Descripción habitual en física: Hay una imagen del rostro detrás del espejo.
• Traducción: El patrón de rayos provenientes del espejo es exactamente el mismo que sería si hubiera una cara detrás del espejo. Nada está realmente detrás del espejo.

Esto se conoce como una imagen virtual, porque los rayos en realidad no se cruzan en el punto detrás del espejo. Sólo parecen haberse originado ahí.

autocomprobación:

Imagínese que la persona en figura a mueve bastante la cara hacia abajo, un par de pies en la vida real, o unos centímetros en este dibujo a escala. El espejo se queda donde está. Dibuja un nuevo diagrama de rayos. ¿Todavía habrá una imagen? Si es así, ¿desde dónde es visible?

(respuesta en la parte posterior de la versión PDF del libro)

La geometría de la reflexión especular nos dice que los rayos 1 y 2 están en ángulos iguales a la normal (la línea perpendicular imaginaria que perfora el espejo en el punto de reflexión). Esto significa que la continuación imaginaria del rayo 2, 3, forma el mismo ángulo con el espejo que el rayo 1. Dado que cada rayo de tipo 3 forma los mismos ángulos con el espejo que su compañero de tipo 1, vemos que la distancia de la imagen desde el espejo es la misma que la de la cara real del espejo, y se encuentra directamente frente a él. Por lo tanto, la imagen parece tener el mismo tamaño que la cara real.

b/Ejemplo 2.

Ejemplo 2: Un examen de la vista
La figura b muestra una configuración típica en una sala de examen de optometrista. Se supone que la visión del paciente debe ser evaluada a una distancia de 6 metros (20 pies en EE.UU.), pero esta distancia es mayor que la cantidad de espacio disponible en la habitación. Por lo tanto, se utiliza un espejo para crear una imagen de la carta ocular detrás de la pared.

Ejemplo 3: El praxinoscopio

c/El praxinoscopio. La figura c muestra un dispositivo anticuado llamado praxinoscopio, que muestra una imagen animada cuando se gira. La tira de papel extraíble con las imágenes impresas en ella tiene el doble de radio del círculo interno hecho de espejos planos, por lo que la imagen virtual de cada imagen está en el centro. A medida que gira la rueda, la imagen de cada imagen es reemplazada por la siguiente.

Pregunta de Discusión

◊ La figura muestra un objeto que está apagado a un lado de un espejo. Dibuja un diagrama de rayos. ¿Se forma una imagen? Si es así, ¿dónde está y desde qué direcciones sería visible?

12.2.2 Espejos curvos

Una imagen en un espejo plano es un ejemplo pretecnológico: incluso los animales pueden mirar sus reflejos en un estanque tranquilo. Pasamos ahora a nuestro primer ejemplo no trivial de la manipulación de una imagen por la tecnología: una imagen en un espejo curvo. Antes de sumergirnos, consideremos por qué este es un ejemplo importante. Si solo se tratara de memorizar un montón de datos sobre los espejos curvos, entonces, con razón, te rebelarías contra un esfuerzo por estropear la belleza de tu cerebro generosamente educado alimentándote a la fuerza trivia tecnológica. La razón por la que este es un ejemplo importante no es que los espejos curvos sean tan importantes en sí mismos, sino que los resultados que obtenemos para los espejos curvos en forma de cuenco resultan ser ciertos para una gran clase de otros dispositivos ópticos, incluidos los espejos que sobresalen hacia afuera en lugar de hacia adentro, y las lentes también. Un microscopio o un telescopio es simplemente una combinación de lentes o espejos o ambos. Lo que realmente estás aprendiendo aquí es el componente básico de todos los dispositivos ópticos, desde proyectores de películas hasta ojos de pulpo.

d/Una imagen formada por un espejo curvo.

Debido a que el espejo en la figura d es curvo, dobla los rayos de nuevo más cerca de lo que lo haría un espejo plano: lo describimos como convergente. Tenga en cuenta que el término se refiere a lo que hace a los rayos de luz, no a la forma física de la superficie del espejo. (La superficie en sí sería descrita como cóncava. El término no es tan difícil de recordar, porque el interior ahuecado del espejo es como una cueva.) Es sorprendente pero cierto que todos los rayos como 3 realmente convergen en un punto, formando una buena imagen. No vamos a probar este hecho, pero es cierto para cualquier espejo cuya curvatura sea lo suficientemente suave y que sea simétrica con respecto a la rotación alrededor de la línea perpendicular que pasa por su centro (no asimétrica como una papa frita). El método anticuado de hacer espejos y lentes es moliéndolos en grano a mano, y esto tiende automáticamente a producir una superficie esférica casi perfecta.

Doblar un rayo como 2 hacia adentro implica doblar su continuación imaginaria 3 hacia afuera, de la misma manera que levantar un extremo de un balancín hace que el otro extremo baje. Por lo tanto, la imagen se forma más profunda detrás del espejo. Esto no solo demuestra que hay una distancia extra entre la imagen-nariz y el espejo; también implica que la imagen en sí es más grande de adelante hacia atrás. Se ha magnificado en la dirección de adelante hacia atrás.

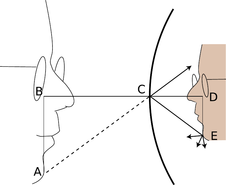
e/La imagen se magnifica por el mismo factor en profundidad y en sus otras dimensiones.

Es fácil demostrar que la misma ampliación también se aplica a las otras dimensiones de la imagen. Considera un punto como E en la figura e. el truco es que de todos los rayos reflejados difusamente por E, elegimos el que pasa a dirigirse hacia el centro del espejo, C. La propiedad de ángulo igual de la reflexión especular más una geometría poco sencilla nos lleva fácilmente a la conclusión de que los triángulos ABC y CDE tienen la misma forma, siendo ABC simplemente una versión ampliada de CDE. El aumento de profundidad es igual a la relación BC/CD, y el aumento arriba-abajo es AB/DE. Una repetición de la misma prueba muestra que la ampliación en la tercera dimensión (fuera de la página) es también la misma. Esto significa que el cabezal de imagen es simplemente una versión más grande de la real, sin distorsión alguna. El factor de escala se llama el aumento,\(M\). La imagen en la figura se magnifica por un factor\(M=1.9\).

f/El aumento de aumento siempre viene a expensas de la disminución del campo de visión.

Tenga en cuenta que no especificamos explícitamente si el espejo era una esfera, un paraboloide o alguna otra forma. No obstante, asumimos que se formaría una imagen enfocada, lo que no necesariamente sería cierto, por ejemplo, para un espejo que fuera asimétrico o muy curvado.

12.2.3 Una imagen real

Si comenzamos colocando un objeto muy cerca del espejo, g/1, y luego lo movemos cada vez más lejos, la imagen al principio se comporta como esperaríamos de nuestra experiencia cotidiana con espejos planos, retrocediendo cada vez más detrás del espejo. En cierto punto, sin embargo, se produce un cambio dramático. Cuando el objeto está a más de una cierta distancia del espejo, g/2, la imagen aparece boca abajo y frente al espejo.

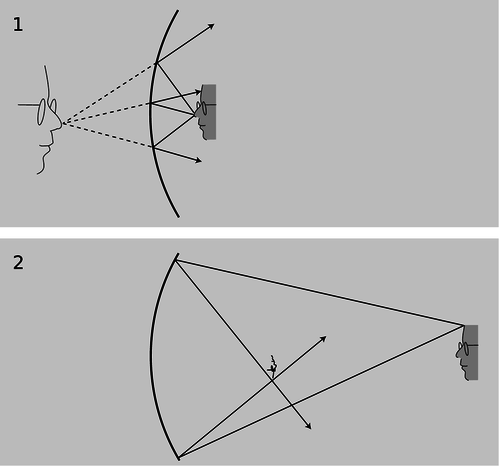
g/1. Una imagen virtual. 2. Una imagen real. Como verificarás en el problema de tarea 12, la imagen está al revés

Esto es lo que ha pasado. El espejo dobla los rayos de luz hacia adentro, pero cuando el objeto está muy cerca de él, como en g/1, los rayos que vienen de un punto dado sobre el objeto son demasiado divergentes (extendiéndose) fuertemente para que el espejo los vuelva a unir. Al reflexionar, los rayos siguen divergiendo, pero no tan fuertemente divergentes. Pero cuando el objeto está lo suficientemente lejos, g/2, el espejo sólo está interceptando los rayos que salieron en un cono estrecho, y es capaz de doblarlos lo suficiente para que vuelvan a converger.

Obsérvese que los rayos mostrados en la figura, que ambos se originaron en el mismo punto sobre el objeto, se reúnen cuando se cruzan. El punto donde cruzan es la imagen del punto sobre el objeto original. Este tipo de imagen se llama imagen real, en contraposición a las imágenes virtuales que hemos estudiado antes.

Definición: Una imagen real es aquella en la que los rayos realmente se cruzan. Una imagen virtual es un punto del que los rayos sólo parecen haber llegado.

El uso de la palabra “real” es quizás desafortunado. Suena como si estuviéramos diciendo que la imagen era un objeto material real, que por supuesto no lo es.

La distinción entre una imagen real y una imagen virtual es importante, porque una imagen real puede proyectarse sobre una pantalla o película fotográfica. Si se inserta un trozo de papel en la figura g/2 en la ubicación de la imagen, la imagen será visible en el papel (siempre que el objeto sea brillante y la habitación esté oscura). Tu ojo usa una lente para hacer una imagen real en la retina.

autocomprobación:

Dibuja otra copia de la cara en la figura g/1, aún más lejos del espejo, y dibuja un diagrama de rayos. ¿Qué ha pasado con la ubicación de la imagen?

(respuesta en la parte posterior de la versión PDF del libro)

12.2.4 Imágenes de imágenes

Si estás usando anteojos ahora mismo, entonces los rayos de luz de la página están siendo manipulados primero por tus gafas y luego por la lente de tu ojo. Se podría pensar que sería sumamente difícil analizar esto, pero de hecho es bastante fácil. En cualquier serie de elementos ópticos (espejos o lentes o ambos), cada elemento trabaja sobre los rayos proporcionados por el elemento anterior exactamente de la misma manera que si la imagen formada por el elemento anterior fuera un objeto real.

h/Un telescopio newtoniano que se utiliza con una cámara.

La figura h muestra un ejemplo que involucra solo espejos. El telescopio newtoniano, inventado por Isaac Newton, consiste en un gran espejo curvo, más un segundo espejo plano que saca la luz del tubo. (En telescopios muy grandes, puede haber suficiente espacio para poner una cámara o incluso una persona dentro del tubo, en cuyo caso no se necesita el segundo espejo). El tubo del telescopio no es vital; es principalmente un elemento estructural, aunque también puede ser útil para bloquear la luz parásita. El objetivo se ha quitado de la parte frontal del cuerpo de la cámara y no es necesario para esta configuración. Tenga en cuenta que los dos rayos de muestra se han dibujado paralelos, debido a que se utiliza un telescopio astronómico para visualizar objetos que están extremadamente lejos. Estas dos líneas “paralelas” realmente se encuentran en cierto punto, digamos un cráter en la luna, por lo que en realidad no pueden ser perfectamente paralelas, pero son paralelas para todos los fines prácticos ya que tendríamos que seguirlas hacia arriba por un cuarto de millón de millas para llegar al punto en que se cruzan.

i/Un telescopio newtoniano que se utiliza para la observación visual más que fotográfica. En la vida real, normalmente se usa una lente ocular para un aumento adicional, pero esta configuración más simple también funcionará.

El gran espejo curvo por sí mismo formaría una imagen\(\text{I}\), pero el pequeño espejo plano crea una imagen de la imagen,\(\text{I}'\). La relación entre\(\text{I}\) y\(\text{I}'\) es exactamente la misma que sería si\(\text{I}\) fuera un objeto real más que una imagen:\(\text{I}\) y\(\text{I}'\) están a distancias iguales del plano del espejo, y la línea entre ellos es perpendicular al plano del espejo.

Una arruga sorprendente es que mientras que un espejo plano utilizado por sí mismo forma una imagen virtual de un objeto que es real, aquí el espejo está formando una imagen real de imagen virtual\(\text{I}\). Esto demuestra lo inútil que sería tratar de memorizar listas de hechos sobre qué tipo de imágenes están formadas por diversos elementos ópticos bajo diversas circunstancias. Es mejor que simplemente dibujes un diagrama de rayos.

j/El tamaño angular de la flor depende de su distancia al ojo.

Si bien el punto principal aquí fue dar un ejemplo de una imagen de una imagen, la figura i también muestra un caso interesante donde necesitamos hacer la distinción entre aumento y aumento angular. \(\text{I}\)f estás mirando la luna a través de este telescopio, entonces las imágenes\(\text{I}\) y\(\text{I}'\) son mucho más pequeñas que la luna real. De lo contrario, por ejemplo, ¡la imagen no\(\text{I}\) cabría dentro del telescopio! Sin embargo, estas imágenes están muy cerca de tu ojo en comparación con la luna real. El pequeño tamaño de la imagen ha sido más que compensado por la distancia más corta. Lo importante aquí es la cantidad de ángulo dentro de su campo de visión que cubre la imagen, y es este ángulo el que se ha incrementado. El factor por el cual se incrementa se llama el aumento angular,\(M_a\).

k/La persona usa un espejo para obtener una vista de ambos lados de la mariquita. A pesar de que el espejo plano tiene\(M=1\), no da un aumento angular de 1. La imagen está más lejos del ojo que del objeto, por lo que el aumento angular\(M_a=\alpha_i/\alpha_o\) es menor que uno.

Preguntas de Discusión

◊ Localiza las imágenes tuyas que se formarán si te paras entre dos espejos paralelos.

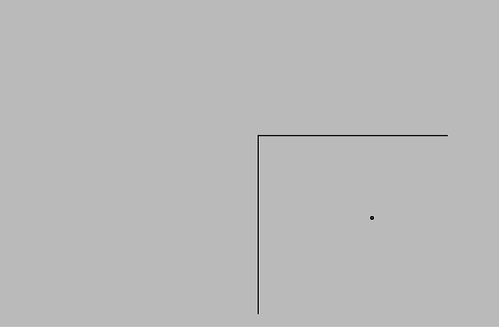
◊ Localizar las imágenes formadas por dos espejos perpendiculares, como en la figura. ¿Qué pasa si los espejos no son perfectamente perpendiculares?

◊ Localizar las imágenes formadas por el periscopio.

Colaborador

Template:ContribCrowell