13.E: Óptica (Ejercicios)

1. Dibuja un diagrama de rayos que muestre por qué una pequeña fuente de luz (una vela, digamos) produce sombras más nítidas que una grande (por ejemplo, una bombilla fluorescente larga).

2. Un receptor del Sistema de Posicionamiento Global (GPS) es un dispositivo que le permite averiguar dónde se encuentra al recibir señales de radio cronometradas de los satélites. Funciona midiendo el tiempo de viaje de las señales, lo cual está relacionado con la distancia entre usted y el satélite. Al encontrar los rangos a varios satélites diferentes de esta manera, puede precisar tu ubicación en tres dimensiones a unos pocos metros. ¿Qué tan precisa tiene que ser la medición del retardo de tiempo para determinar su posición con esta precisión?

3. Estimar la frecuencia de una onda electromagnética cuya longitud de onda es similar en tamaño a un átomo (aproximadamente un nm). Refiriéndose de nuevo a la figura o de la p. 703, ¿en qué parte del espectro electromagnético se encontraría tal onda (infrarrojos, rayos gamma,...)?

4. El bombardero Stealth está diseñado con superficies planas y lisas. ¿Por qué esto dificultaría la detección vía radar?

a/Problema 5.

5. Los nativos del planeta Wumpus juegan al billar usando rayos de luz sobre una mesa de once lados con espejos para parachoques, que se muestra en la figura de la página siguiente. Rastrea esta toma con precisión con una regla para revelar el mensaje oculto. Para obtener una precisión lo suficientemente buena, necesitarás fotocopiar la página (o descargar el libro e imprimir la página) y construir cada reflexión usando un transportador.

b/Problema 6.

6. La figura de la siguiente página muestra un espejo curvo (parabólico), con tres rayos de luz paralelos que llegan hacia él. Un rayo se acerca a lo largo de la línea central del espejo. a) Trazar el dibujo con precisión, y continuar los rayos de luz hasta que estén a punto de someterse a su segundo reflejo. Para obtener una precisión lo suficientemente buena, necesitarás fotocopiar la página (o descargar el libro e imprimir la página) y dibujar en la normalidad en cada lugar donde se refleje un rayo. ¿Qué notas? b) Formular un ejemplo de uso práctico para este dispositivo. (c) ¿Cómo podría usar este espejo con una pequeña bombilla para producir un haz paralelo de rayos de luz que se apagan hacia la derecha?

7. (consulta de respuesta disponible en lightandmatter.com) Un hombre camina a 1.0 m/s directamente hacia un espejo plano. ¿A qué velocidad disminuye su separación de su imagen?

8. Si un espejo en una pared solo es lo suficientemente grande como para que te veas desde la cabeza hasta la cintura, ¿puedes ver todo tu cuerpo retrocediendo? Prueba esto experimentalmente y haz una explicación para tus observaciones, incluyendo un diagrama de rayos.

Ten en cuenta que cuando haces el experimento, es fácil confundirte si el espejo está incluso un poquito fuera de la vertical. Una forma de comprobarse es bajar artificialmente la parte superior del espejo poniendo un trozo de cinta o una nota post-it donde bloquea tu vista de la parte superior de tu cabeza. Luego puedes verificar si puedes ver más de ti mismo tanto arriba como abajo haciendo una copia de seguridad.

9. En la sección 12.2 solo hemos hecho ejemplos de espejos con formas ahuecadas (llamados espejos cóncavos). Ahora dibuja un diagrama de rayos para un espejo curvo que tenga una forma abultada hacia afuera (llamado espejo convexo). (a) ¿Cómo se compara la distancia de la imagen al espejo con la distancia real del objeto al espejo? A partir de esta comparación, determinar si el aumento es mayor o menor que uno. b) ¿La imagen es real, o virtual? ¿Podría este espejo hacer alguna vez el otro tipo de imagen?

10. Como se discutió en la pregunta 9, existen dos tipos de espejos curvos, cóncavos y convexos. Hacer una lista de todas las posibles combinaciones de tipos de imágenes (virtuales o reales) con tipos de espejos (cóncavos y convexos). (No todas las cuatro combinaciones son físicamente posibles). Ahora para cada uno, use diagramas de rayos para determinar si aumentar la distancia del objeto desde el espejo conduce a un aumento o una disminución en la distancia de la imagen desde el espejo.

¡Dibuja BIG diagramas de rayos! Cada diagrama debe agotar aproximadamente media página de papel.

Algunos consejos: Para dibujar un diagrama de rayos, se necesitan dos rayos. Para uno de estos, escoge el rayo que viene recto a lo largo del eje del espejo, ya que su reflejo es fácil de dibujar. Después de dibujar los dos rayos y ubicar la imagen para la posición original del objeto, elija una nueva posición de objeto que dé como resultado el mismo tipo de imagen, e inicie un nuevo diagrama de rayos, en un color diferente de pluma, justo encima del primero. Para los dos nuevos rayos, elige los que acaba de suceder que golpeen el espejo en los mismos dos lugares; esto hace que sea mucho más fácil obtener el resultado correcto sin depender de una precisión extrema en tu capacidad para dibujar los rayos reflejados.

11. Si el usuario de un telescopio astronómico mueve su cabeza más cerca o más lejos de la imagen que está mirando, ¿cambia la ampliación? ¿Cambia el aumento angular? Explique. (Por simplicidad, supongamos que no se está utilizando ningún ocular).

12. En la figura g/2 en la página 752, sólo se localizó la imagen de mi frente dibujando rayos. Ya sea fotocopiar la figura o descargar el libro e imprimir la página correspondiente. En esta copia de la figura, haz un nuevo conjunto de rayos provenientes de mi barbilla, y localiza su imagen. Para que sea más fácil juzgar los ángulos con precisión, dibuja rayos del mentón que por casualidad chocan con el espejo en los mismos puntos donde se mostraban los dos rayos de la frente golpeándolo. Al comparar las ubicaciones de la imagen del mentón y la imagen de la frente, verificar que la imagen esté realmente al revés, como se muestra en la figura original.

c/Problema 13.

13. La figura muestra cuatro puntos donde se cruzan los rayos. De estos, ¿cuáles son los puntos de imagen? Explique.

14. Aquí hay un juego que a mis hijos les gusta jugar. Me siento junto a una ventana soleada, y el sol se refleja desde el cristal de mi reloj, haciendo un disco de luz en la pared o el piso, que pretenden perseguir mientras lo muevo. ¿El spot es un disco porque esa es la forma del sol, o porque es la forma de mi reloj? En otras palabras, ¿un reloj cuadrado haría una mancha cuadrada, o simplemente tenemos una imagen circular del sol circular, que será circular pase lo que pase?

15. Aplicar la ecuación\(M=d_i/d_o\) al caso de un espejo plano.

16. (solución en la versión pdf del libro) Utilice el método descrito en el texto para derivar la ecuación que relaciona la distancia del objeto con la distancia de la imagen para el caso de una imagen virtual producida por un espejo convergente.

17. Encuentra la distancia focal del espejo en problema 6. (consulta de respuesta disponible en lightandmatter.com)

d/Problema 18.

18. Clasificar las distancias focales de los espejos en la figura, de la más corta a la más larga. Explique.

19. (solución en la versión pdf del libro) (a) Se utiliza un espejo convergente con una distancia focal de 20 cm para crear una imagen, utilizando un objeto a una distancia de 10 cm. ¿La imagen es real, o es virtual? b) ¿Qué tal\(f=20\) cm y\(d_o=30\) cm? (c) ¿Y si se tratara de un espejo divergente con\(f=20\) cm y\(d_o=10\) cm? (d) Un espejo divergente con\(f=20\) cm y\(d_o=30\) cm?

20. a) Formular un ejemplo numérico de una imagen virtual formada por un espejo convergente con cierta distancia focal, y determinar el aumento. (Necesitarás el resultado del problema 16.) Asegúrese de elegir valores de\(d_o\) y\(f\) eso realmente produciría una imagen virtual, no una real. Ahora cambia un poco la ubicación del objeto y vuelve a determinar la ampliación, mostrando que cambia. En mi tienda departamental local, el departamento de cosméticos vende espejos de mano anunciados como dando una ampliación de 5 veces. ¿Cómo interpretarías esto?

b) Supongamos que se está utilizando un telescopio newtoniano para la observación astronómica. Asumir por simplicidad que no se usa ningún ocular, y asumir un valor para la distancia focal del espejo que sería razonable para un instrumento amateur que es para caber en un armario. ¿El aumento angular es diferente para los objetos a diferentes distancias? Por ejemplo, podrías considerar dos planetas, uno de los cuales es el doble que el otro.

21. (a) Encontrar un caso donde el aumento de un espejo curvo sea infinito. ¿La ampliación angular es infinita desde cualquier posición de visualización realista? (b) Explicar por qué no se puede lograr una ampliación arbitrariamente grande al tener un valor suficientemente pequeño de\(d_o\).

22. Una superficie cóncava que refleja las ondas sonoras puede actuar como un espejo convergente. Supongamos que, de pie cerca de tal superficie, puedas encontrar un punto donde puedas colocar tu cabeza para que tus propios susurros se centren de nuevo en tu cabeza, para que te suenen fuerte. Dada su distancia a la superficie, ¿cuál es la distancia focal de la superficie?

e/Problema 23.

23. La figura muestra un dispositivo para construir una ilusión óptica realista. Dos espejos de igual distancia focal se colocan uno contra el otro con sus superficies plateadas orientadas hacia adentro. Un pequeño objeto colocado en el fondo de la cavidad tendrá su imagen proyectada en el aire de arriba. La forma en que funciona es que el espejo superior produce una imagen virtual, y el espejo inferior crea entonces una imagen real de la imagen virtual. (a) Mostrar que si la imagen se va a colocar como se muestra, en la boca de la cavidad, entonces la distancia focal de los espejos se relaciona con la dimensión a\(h\) través de la ecuación

\[\begin{equation*} \frac{1}{f} = \frac{1}{h}+\frac{1}{h+\left(\frac{1}{h}-\frac{1}{f}\right)^{-1}} . \end{equation*}\]

(b) Reafirmar la ecuación en términos de una sola variable\(x=h/f\), y mostrar que existen dos soluciones para\(x\). ¿Qué solución es físicamente consistente con los supuestos del cálculo?

24. (a) Se está utilizando un espejo convergente para crear una imagen virtual. ¿Cuál es el rango de posibles aumentos? (b) Hacer lo mismo para los otros tipos de imágenes que puedan estar formadas por espejos curvos (tanto convergentes como divergentes).

25. Un espejo divergente de distancia focal\(f\) es fijo y mira hacia abajo. Un objeto se deja caer de la superficie del espejo, y se aleja de él con aceleración\(g\). El objetivo del problema es encontrar la velocidad máxima de la imagen.
(a) Describir verbalmente el movimiento de la imagen, y explicar por qué debemos esperar que haya una velocidad máxima.
b) Utilizar argumentos basados en unidades para determinar la forma de la solución, hasta una constante multiplicativa sin unidades desconocida.
(c) Completar la solución determinando la constante sin unidades.

26. El diamante tiene un índice de refracción de 2.42, y parte de la razón por la que los diamantes brillan es que esto fomenta que un rayo de luz sufra muchas reflexiones internas totales antes de que emerja. (a) Calcular el ángulo crítico en el que se produce la reflexión interna total en el diamante. (consulta de respuesta disponible en lightandmatter.com) (b) Explica la interpretación de tu resultado: ¿Se mide desde lo normal, o desde la superficie? ¿Es un mínimo, o un máximo? ¿En qué se diferenciaría el ángulo crítico para una sustancia como el vidrio o el plástico, con un menor índice de refracción?

27. Supongamos que una lente convergente está construida de un tipo de plástico cuyo índice de refracción es menor que el del agua. ¿En qué se diferenciará el comportamiento de la lente si se coloca bajo el agua?

28. Hay dos tipos principales de telescopios, refractarios (usando una lente) y reflectantes (usando un espejo, como en la figura i en la p. 754). (Algunos telescopios utilizan una mezcla de los dos tipos de elementos: la luz primero se encuentra con un gran espejo curvo, y luego pasa a través de un ocular que es una lente. Para mantener las cosas simples, supongamos que no se usa ningún ocular.) ¿Qué implicaciones tendría la dependencia del color de la distancia focal para los méritos relativos de los dos tipos de telescopios? Describir el caso donde se forma una imagen de una estrella blanca. Puede resultarle útil dibujar un diagrama de rayos.

29. Con base en la ley de Snell, explica por qué los rayos de luz que pasan por los bordes de una lente convergente se doblan más que los rayos que pasan por partes más cercanas al centro. Podría parecer que debería ser al revés, ya que los rayos en el borde pasan por menos vidrio — ¿no deberían verse afectados menos? En su respuesta:

• Incluye un diagrama de rayos que muestre una vista enorme, de página completa, en primer plano de la parte relevante de la lente.
• Aprovecha el hecho de que las superficies frontal y posterior no siempre son paralelas; una lente en la que las superficies frontal y posterior son siempre paralelas no enfoca la luz en absoluto, por lo que si tu explicación no hace uso de este hecho, tu argumento debe ser incorrecto.
• Asegúrate de que tu argumento siga funcionando aunque los rayos no vengan en paralelo al eje.

30. Cuando tomas fotos con una cámara, se tiene que ajustar la distancia entre la lente y la película, dependiendo de la distancia a la que quieras enfocar. Esto se hace moviendo la lente. Si quieres cambiar tu enfoque para que puedas tomar una foto de algo más lejos, ¿de qué manera tienes que mover la lente? Explicar usando diagramas de rayos. [Basado en un problema de Eric Mazur.]

31. Al nadar bajo el agua, ¿por qué tu visión se hace mucho más clara al usar gafas con trozos planos de vidrio que atrapan el aire detrás de ellos? [Pista: Puedes simplificar tu razonamiento considerando el caso especial en el que estás mirando un objeto muy lejos, y a lo largo del eje óptico del ojo.]

32. (verificación de respuestas disponible en lightandmatter.com) Un objeto tiene más de una distancia focal de una lente convergente. (a) Dibujar un diagrama de rayos. b) Utilizando razonamientos como el desarrollado en la sección 12.3, determinar los signos positivos y negativos en la ecuación\(1/f=\pm1/d_i\pm1/d_o\). (c) Las imágenes de la rosa en la sección 4.2 se realizaron utilizando una lente con una distancia focal de 23 cm. Si la lente se coloca a 80 cm de la rosa, ubique la imagen.

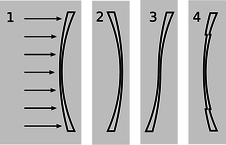
f/Problema 33.

33. La figura muestra cuatro lentes. La lente 1 tiene dos superficies esféricas. La lente 2 es la misma que la lente 1 pero da la vuelta. La lente 3 se fabrica cortando a través de la lente 1 y girando la parte inferior alrededor. La lente 4 se realiza cortando un círculo central de la lente 1 y rebajándola.

(a) Un haz de luz paralelo ingresa a la lente 1 desde la izquierda, paralelo a su eje. Razonamiento basado en la ley de Snell, ¿el haz que emerge de la lente se doblará hacia adentro o hacia afuera, o permanecerá paralelo al eje? Explica tu razonamiento. Como parte de tu respuesta, haz un dibujo enorme de una pequeña parte de la lente y aplica la ley de Snell en ambas interfaces. Recordemos que los rayos se doblan más si llegan a la interfaz en un ángulo mayor con respecto a la normal.

b) ¿Qué pasará con las lentes 2, 3 y 4? Explique. Los dibujos no son necesarios.

g/Problema 34.

34. El dibujo muestra la anatomía del ojo humano, al doble de tamaño natural. Encontrar el radio de curvatura de la superficie exterior de la córnea mediante mediciones en la figura, para luego derivar la distancia focal de la interfaz aire-córnea, donde se produce casi todo el enfoque de la luz. Necesitará usar el razonamiento físico para modificar la ecuación del fabricante de lentes para el caso en que solo haya una sola superficie refractante. Supongamos que el índice de refracción de la córnea es esencialmente el del agua.

35. (verificación de respuestas disponible en lightandmatter.com) Un objeto tiene menos de una distancia focal de una lente convergente. (a) Dibujar un diagrama de rayos. b) Utilizando razonamientos como el desarrollado en la sección 12.3, determinar los signos positivos y negativos en la ecuación\(1/f=\pm1/d_i\pm1/d_o\). (c) Las imágenes de la rosa en la sección 4.2 se realizaron utilizando una lente con una distancia focal de 23 cm. Si la lente se coloca a 10 cm de la rosa, ubique la imagen.

36. (consulta de respuesta disponible en lightandmatter.com) Las personas miopes usan anteojos cuyas lentes son divergentes. (a) Dibujar un diagrama de rayos. Por simplicidad finge que no hay ojo detrás de las gafas. b) Utilizando razonamientos como el desarrollado en la sección 12.3, determinar los signos positivos y negativos en la ecuación\(1/f=\pm1/d_i\pm1/d_o\). (c) Si la distancia focal de la lente es de 50.0 cm, y la persona está mirando un objeto a una distancia de 80,0 cm, localice la imagen.

37. a) La luz está siendo reflejada difusamente desde un objeto 1.000 m bajo el agua. La luz que llega a la superficie se refracta en la interfaz agua-aire. Si todos los rayos refractados parecen provenir del mismo punto, entonces habrá una imagen virtual del objeto en el agua, por encima de la posición real del objeto, que será visible para un observador sobre el agua. Considera tres rayos, A, B y C, cuyos ángulos en el agua con respecto a la normal son\(\theta_i=0.000°\),\(1.000°\) y\(20.000°\) respectivamente. Encuentra la profundidad del punto en el que las partes refractadas de A y B parecen haberse intersectado, y haz lo mismo para A y C. Demuestre que las intersecciones están casi a la misma profundidad, pero no del todo. [Comprobar: La diferencia de profundidad debe ser de unos 4 cm.]

(b) Como no parece que todos los rayos refractados hayan venido del mismo punto, técnicamente no se trata de una imagen virtual. En términos prácticos, ¿qué efecto tendría esto en lo que ves?

(c) En el caso de que todos los ángulos sean pequeños, utilice álgebra y trigonometría para mostrar que los rayos refractados sí parecen provenir del mismo punto, y encontrar una ecuación para la profundidad de la imagen virtual. No pongas ningún valor numérico para los ángulos o para los índices de refracción, solo manténgalos como símbolos. Necesitará la aproximación\(\sin\theta\approx \tan\theta\approx \theta\), la cual es válida para ángulos pequeños medidos en radianes.

38. Demostrar que el principio de menor tiempo lleva a la ley de Snell.

h/Problema 39.

39. (solución en la versión pdf del libro) Dos distancias focales estándar para lentes de cámara son de 50 mm (estándar) y 28 mm (gran angular). Para ver cómo se relacionan las distancias focales con el tamaño angular del campo de visión, es útil visualizar las cosas como se representa en la figura. En lugar de mostrar muchos rayos provenientes del mismo punto sobre un mismo objeto, como lo hacemos normalmente, la figura muestra dos rayos de dos objetos diferentes. Si bien la lente interceptará infinitamente muchos rayos de cada uno de estos puntos, solo hemos mostrado los que pasan por el centro de la lente, para que no sufran deflexión angular. (Cualquier deflexión angular en la superficie frontal de la lente se cancela por una deflexión opuesta en la parte posterior, ya que las superficies frontal y posterior son paralelas en el centro de la lente). Lo especial de estos dos rayos es que están dirigidos a los bordes de un marco de película de 35 mm de ancho; es decir, muestran los límites del campo de visión. A lo largo de este problema, asumimos que\(d_o\) es mucho mayor que\(d_i\). (a) Calcular el ancho angular del campo de visión de la cámara cuando se utilizan estos dos lentes. (b) Utilizar aproximaciones de ángulo pequeño para encontrar una ecuación simplificada para el ancho angular del campo de visión\(\theta \), en términos de la distancia focal\(f\), y el ancho de la película,\(w\). Tu ecuación no debe tener ninguna función trigonométrica en ella. Compare los resultados de esta aproximación con sus respuestas de la parte a. (c) Supongamos que estamos manteniendo constante la apertura (cantidad de área de superficie de la lente que se utiliza para recoger la luz). Al cambiar de una lente de 50 mm a una lente de 28 mm, ¿cuántas veces más larga o más corta debe ser la exposición para hacer una imagen correctamente desarrollada, es decir, una que no esté subexpuesta o sobreexpuesta? [Basado en un problema de Arnold Arons.]

40. Una persona miope es aquella cuyos ojos enfocan la luz con demasiada fuerza, y que por lo tanto es incapaz de relajar la lente dentro de su ojo lo suficiente como para formar una imagen en su retina de un objeto que está demasiado lejos.

(a) Dibujar un diagrama de rayos que muestre lo que sucede cuando la persona intenta, con visión no corregida, enfocar al infinito.

b) ¿Qué tipo de lentes tienen sus gafas? Explique.

(c) Dibujar un diagrama de rayos que muestre lo que sucede cuando usa anteojos. Localiza tanto la imagen formada por las gafas como la imagen final.

d) Supongamos que a veces usa lentes de contacto en lugar de sus anteojos. ¿La distancia focal de sus contactos tiene que ser menor, igual o mayor que la de sus gafas? Explique.

41. Los ojos de Fred son capaces de enfocarse en las cosas tan cerca como 5.0 cm. Fred sostiene una lupa con una distancia focal de 3.0 cm a una altura de 2.0 cm por encima de un gusano plano. (a) Localice la imagen y encuentre el aumento. (b) Sin la lupa, ¿a qué distancia querría Fred ver al gusano plano para ver sus detalles lo mejor posible? ¿Con la lupa? (c) Calcular el aumento angular.

i/Problema 42.

42. El panel 1 de la figura muestra la óptica dentro de un par de binoculares. Son esencialmente un par de telescopios, uno por cada ojo. Pero para hacerlos más compactos, y permitir que los oculares estén a la distancia adecuada para un rostro humano, incorporan un conjunto de ocho prismas, que pliegan el camino de la luz. Además, los prismas hacen que la imagen quede erguida. El panel 2 muestra uno de estos prismas, conocido como prisma de Porro. La luz entra a lo largo de una normal, experimenta dos reflexiones internas totales en ángulos de 45 grados con respecto a las superficies posteriores, y sale a lo largo de una normal. La imagen de la letra R ha sido volteada a través de la horizontal. El panel 3 muestra un par de estos prismas pegados entre sí. La imagen se volteará tanto en la horizontal como en la vertical, lo que la hace orientada de la manera correcta para el usuario de los binoculares.

a) Encontrar el índice mínimo posible de refracción para el vidrio utilizado en los prismas.
(b) Para un material de este índice mínimo de refracción, encuentre la fracción de la luz entrante que se perderá por reflexión en los cuatro prismas Porro a cada lado de un par de binoculares. (Ver sección 6.2.) En binoculares reales de alta calidad, las superficies ópticas de los prismas cuentan con recubrimientos antirreflectantes, pero realiza tu cálculo para el caso en que no exista tal recubrimiento.
(c) Discutir las razones por las que un diseñador de binoculares podría o no querer usar un material con exactamente el índice de refracción que se encuentra en la parte a.

43. Sería molesto que tus anteojos produjeran una imagen magnificada o reducida. Demostrar que cuando el ojo está muy cerca de una lente, y la lente produce una imagen virtual, la ampliación angular siempre es aproximadamente igual a 1 (independientemente de si la lente es divergente o convergente).

44. La figura muestra un patrón de difracción realizado por una doble rendija, junto con una imagen de una varilla métrica para mostrar la escala. Esboce el patrón de difracción de la figura en tu papel. Consideremos ahora las cuatro variables en la ecuación\(\lambda /d=\sin \theta /m\). ¿Cuáles de estos son los mismos para los cinco flecos y cuáles son diferentes para cada franja? ¿Qué variable usarías naturalmente para etiquetar qué franja era cuál? Etiquete los flecos en su boceto usando los valores de esa variable.

45. Haga coincidir las rejillas A-C con los patrones de difracción 1-3 que producen. Explique.

46. La siguiente figura muestra dos patrones de difracción. El de arriba se hizo con luz amarilla, y el inferior con rojo. ¿Podrían las hendiduras utilizadas para hacer los dos patrones haber sido las mismas?

j/Problemas 44 y 47.

47. La figura de la p. 805 muestra un patrón de difracción realizado por una doble hendidura, junto con una imagen de una varilla métrica para mostrar la escala. Las hendiduras estaban a 146 cm de distancia de la pantalla sobre la que se proyectó el patrón de difracción. El espaciamiento de las hendiduras fue de 0.050 mm. ¿Cuál era la longitud de onda de la luz? (consulta de respuesta disponible en lightandmatter.com)

48. ¿Por qué la luz azul o violeta sería la mejor para microscopía?

49. La siguiente figura muestra dos patrones de difracción, ambos hechos con la misma longitud de onda de luz roja. a) ¿Qué tipo de hendiduras hicieron los patrones? ¿Es una sola hendidura, rendijas dobles o algo más? Explique. (b) Comparar las dimensiones de las ranuras utilizadas para hacer el patrón superior e inferior. Dé una relación numérica y establezca en qué dirección está la relación, es decir, qué patrón de hendidura fue el más grande. Explique.

50. Cuando la luz blanca pasa a través de una rejilla de difracción, cuál es el valor más pequeño\(m\) para el cual el espectro visible de orden\(m\) se solapa con el siguiente, de orden\(m+1?\) (El espectro visible va desde aproximadamente 400 nm hasta aproximadamente 700 nm.)

k/Problema 51. Esta imagen del cúmulo estelar de las Pléyades muestra halos alrededor de las estrellas debido a la naturaleza ondulada de la luz.

51. Para imágenes de estrellas como las de la figura y, estime el ancho angular del punto de difracción debido a la difracción en la boca del telescopio. Supongamos un telescopio con un diámetro de 10 metros (el más grande actualmente en existencia), y luz con una longitud de onda en el medio del rango visible. Compara con el tamaño angular real de una estrella de diámetro\(10^9\) m vista desde una distancia de\(10^{17}\) m. ¿Qué te dice esto?

52. La siguiente figura muestra tres patrones de difracción. Todos se realizaron en idénticas condiciones, excepto que se utilizó un juego diferente de hendiduras dobles para cada una. Las hendiduras utilizadas para hacer el patrón superior tuvieron una separación de centro a centro\(d=0.50\) mm, y cada hendidura tenía\(w=0.04\) mm de ancho. (a) Determinar\(d\) y\(w\) para las hendiduras utilizadas para hacer el patrón en el medio. (b) Hacer lo mismo con las hendiduras utilizadas para hacer el patrón inferior.

53. (verificación de respuesta disponible en lightandmatter.com) El haz de un láser pasa a través de una rejilla de difracción, se abaniza e ilumina una pared que es perpendicular al haz original, que se encuentra a una distancia de 2.0 m de la rejilla. El haz es producido por un láser de helio-neón, y tiene una longitud de onda de 694.3 nm. La rejilla tiene 2000 líneas por centímetro. a) ¿Cuál es la distancia en la pared entre el máximo central y el máximo inmediatamente a su derecha e izquierda? (b) ¿Cuánto cambia tu respuesta cuando usas las aproximaciones de ángulo pequeño\(\theta\approx\sin\theta\approx\tan\theta\)?

54. El ultrasonido, es decir, las ondas sonoras con frecuencias demasiado altas para ser audibles, pueden usarse para obtener imágenes de fetos en el útero o para romper cálculos renales para que puedan ser eliminados por el cuerpo. Considera esta última aplicación. Se pueden construir lentes para enfocar las ondas sonoras, pero debido a que la longitud de onda del sonido no es tan pequeña en comparación con el diámetro de la lente, el sonido no se concentrará exactamente en el punto focal geométrico. En cambio, se creará un patrón de difracción con un punto central intenso rodeado de anillos más débiles. Alrededor del 85% de la potencia se concentra dentro del punto central. El ángulo del primer mínimo (rodeando el punto central) viene dado por\(\sin \theta =\lambda/b\), donde\(b\) está el diámetro de la lente. Esto es similar a la ecuación correspondiente para una sola hendidura, pero con un factor de 1.22 en frente que surge de la forma circular de la abertura. Deje que la distancia desde el cristalino hasta el cálculo renal del paciente sea\(L=20\) cm. Querrás\(f>20\) kHz, para que el sonido sea inaudible. Encontrar valores de\(b\) y\(f\) que resultarían en un diseño utilizable, donde el punto central es lo suficientemente pequeño como para estar dentro de un cálculo renal de 1 cm de diámetro.

55. ¿Bajo qué circunstancias podría uno obtener un resultado matemáticamente indefinido resolviendo la ecuación de difracción de doble rendija para\(\theta \)? Dar una interpretación física de lo que realmente se observaría.

56. Cuando se usa ultrasonido para imágenes médicas, la frecuencia puede ser tan alta como 5-20 MHz. Otra aplicación médica del ultrasonido es para el calentamiento terapéutico de los tejidos dentro del cuerpo; aquí, la frecuencia suele ser de 1-3 MHz. ¿Qué razones físicas fundamentales podría sugerir para el uso de frecuencias más altas para la obtención de imágenes?

l/Problema 57.

57. Supongamos que tenemos una habitación poligonal cuyas paredes son espejos, y hay una fuente de luz puntual en la habitación. En la mayoría de estos ejemplos, cada punto de la habitación termina siendo iluminado por la fuente de luz después de algún número finito de reflejos. Una cuestión matemática difícil, planteada por primera vez a mediados del siglo pasado, es si alguna vez es posible tener un ejemplo en el que no se ilumine toda la habitación. (Se supone que los rayos son absorbidos si chocan exactamente en un vértice del polígono, o si pasan exactamente a través del plano de un espejo).

El problema fue finalmente resuelto en 1995 por G.W. Tokarsky, quien encontró un ejemplo de una habitación que no era iluminable desde cierto punto. La figura 57 muestra un ejemplo un poco más sencillo encontrado dos años después por D. Castro. Si se coloca una fuente de luz en cualquiera de las ubicaciones mostradas con puntos, el otro punto permanece sin iluminar, aunque cada otro punto está iluminado. No es sencillo probar rigurosamente que la solución de Castro tiene esta propiedad. Sin embargo, la plausibilidad de la solución puede demostrarse de la siguiente manera.

Supongamos que la fuente de luz se coloca en el punto de la derecha. Localice todas las imágenes formadas por reflejos únicos. Tenga en cuenta que forman un patrón regular. Convénzase de que ninguna de estas imágenes ilumina el punto izquierdo. Debido al patrón regular, se vuelve plausible que aunque formemos imágenes de imágenes, imágenes de imágenes de imágenes, etc., ninguna de ellas iluminará nunca el otro punto.

Hay varias otras versiones del problema, algunas de las cuales permanecen sin resolver. El libro de Klee y Wagon da una buena introducción al tema, aunque es anterior a la obra de Tokarsky y Castro.

Referencias:
G.W. Tokarsky, “Habitaciones poligonales no iluminables desde todos los puntos”. Amer. Matemáticas. Mensual 102, 867-879, 1995.
D. Castro, “Correcciones”. Quantum 7, 42, ene. 1997.
V. Klee y S. Wagon, viejos y nuevos problemas sin resolver en geometría de plano y teoría de números. Asociación Matemática de América, 1991.

m/Problema 58.

58. Un varillaje mecánico es un dispositivo que cambia un tipo de movimiento en otro. El ejemplo más familiar ocurre en el motor de un automóvil de gasolina, donde una biela cambia el movimiento lineal del pistón en movimiento circular del cigüeñal. El panel superior de la figura muestra un varillaje mecánico inventado por Peaucellier en 1864, e independientemente por Lipkin aproximadamente al mismo tiempo. Consta de seis varillas unidas por bisagras, las cuatro cortas formando un rombo. El punto O se fija en el espacio, pero el aparato es libre de girar alrededor de O. El movimiento en P se transforma en un movimiento diferente en\(\text{P}'\) (o viceversa).

Geométricamente, el enlace es una implementación mecánica del antiguo problema de la inversión en un círculo. Considerando el caso en el que el rombo se pliega plano, deja que el\(k\) sea la distancia desde O hasta el punto donde P y\(\text{P}'\) coinciden. Formar el círculo de radio\(k\) con su centro en O. Como P y\(\text{P}'\) moverse dentro y fuera, los puntos en el interior del círculo siempre se mapean a puntos en su exterior, de tal manera que\(rr'=k^2\). Es decir, el enlace es un tipo de computadora analógica que resuelve exactamente el problema de encontrar la inversa de un número\(r\). La inversión en círculo tiene muchas propiedades geométricas notables, discutidas en H.S.M. Coxeter, Introducción a la geometría, Wiley, 1961. Si se inserta una pluma a través de un orificio en P, y\(\text{P}'\) se traza sobre una figura geométrica, se puede utilizar el enlace Peaucellier para dibujar una especie de imagen de la figura.

Un problema relacionado es la construcción de cuadros, como el del panel inferior de la figura, llamado anamorfos. El dibujo de la columna sobre el papel está muy distorsionado, pero cuando el cilindro reflectante se coloca en el lugar correcto en la parte superior de la página, se produce una imagen no distorsionada dentro del cilindro. (Las tecnologías de películas de gran formato como Cinemascope se basan en principios similares).

Mostrar que el enlace Peaucellier no convierte correctamente entre una imagen y su anamorfo, y diseñar una versión modificada del enlace que sí. Algunos conocimientos de geometría analítica serán útiles.

n/Problema 59.

59. La figura muestra una lente con superficies curvadas, pero cuyo grosor es constante a lo largo de cualquier línea horizontal. Usa la ecuación del fabricante de lentes para demostrar que esta “lente” no es realmente una lente en absoluto. (solución en la versión pdf del libro)

60. En condiciones ordinarias, los gases tienen índices de refracción sólo un poco mayores que los del vacío, es decir\(n=1+\epsilon\), donde\(\epsilon\) hay algún número pequeño. Supongamos que un rayo cruza un límite entre una región de vacío y una región en la que se encuentra el índice de refracción\(1+\epsilon\). Encuentra el ángulo máximo por el cual tal rayo puede ser desviado alguna vez, en el límite de los pequeños\(\epsilon\). \ hwhint {hwhint:muy débil-refracción}

61. Un espejo convergente tiene distancia focal\(f\). Un objeto se ubica a una\((1+\epsilon)f\) distancia del espejo, donde\(\epsilon\) es pequeño. Encuentra la distancia de la imagen del espejo, simplificando tu resultado tanto como sea posible usando la suposición de que\(\epsilon\) es pequeña. \ hwans {hwans:cerca de la longitud focal}

Contributors and Attributions

Template:ContribCrowell