14.4: El Átomo

Puedes aprender mucho desarmando un motor de auto, pero habrás aprendido mucho más si puedes volver a armarlo todo y hacerlo funcionar. La mitad del trabajo del reduccionismo es descomponer la naturaleza en sus partes más pequeñas y entender las reglas que esas partes obedecen. El segundo tiempo es mostrar cómo van juntas esas partes, y ese es nuestro objetivo en este capítulo. Hemos visto cómo ciertas características de todos los átomos pueden explicarse de manera genérica en términos de las propiedades de los estados ligados, pero este tipo de argumentos claramente no pueden decirnos ningún detalle del comportamiento de un átomo ni explicar por qué un átomo actúa de manera diferente a otro.

La mayor vergüenza para los reduccionistas es que el trabajo de volver a armar las cosas suele ser mucho más difícil que desarmarlas. Setenta años después de que se resolvieran los fundamentos de la física atómica, apenas comienza a ser posible calcular con precisión las propiedades de los átomos que tienen muchos electrones. Los sistemas que constan de muchos átomos son aún más duros. Los fabricantes de supercomputadoras señalan el plegado de grandes moléculas proteicas como un proceso cuyo cálculo apenas es factible con sus máquinas más rápidas. El objetivo de este capítulo es dar una guía suave y visualmente orientada a algunos de los resultados más simples sobre los átomos.

Clasificación de Estados

Centraremos nuestra atención primero en el átomo más simple, el hidrógeno, con un protón y un electrón. Sabemos de antemano un poco de lo que debemos esperar de la estructura de este átomo. Dado que el electrón está unido al protón por fuerzas eléctricas, debe mostrar un conjunto de estados discretos de energía, cada uno correspondiente a un cierto patrón de onda estacionaria. Necesitamos entender qué estados hay y cuáles son sus propiedades.

¿Qué propiedades debemos usar para clasificar los estados? El enfoque más sensato es el uso de cantidades conservadas. La energía es una cantidad conservada, y ya sabemos esperar que cada estado tenga una energía específica. Resulta, sin embargo, que la energía por sí sola no es suficiente. Diferentes patrones de onda estacionaria del átomo pueden tener la misma energía.

El impulso también es una cantidad conservada, pero no es particularmente apropiada para clasificar los estados del electrón en un átomo de hidrógeno. La razón es que la fuerza entre el electrón y el protón da como resultado el intercambio continuo de impulso entre ellos. (¿Por qué no fue esto un problema para la energía también? La energía cinética y el impulso están relacionados por\(K=p^2/2m\), por lo que el protón mucho más masivo nunca tiene mucha energía cinética. Estamos haciendo una aproximación asumiendo que toda la energía cinética está en el electrón, pero es una aproximación bastante buena).

El momento angular ayuda con la clasificación. No hay transferencia de momento angular entre el protón y el electrón, ya que la fuerza entre ellos es una fuerza de centro a centro, no produciendo par.

a/Ocho longitudes de onda encajan alrededor de este círculo (\(\ell=8\)).

Al igual que la energía, el momento angular se cuantifica en la física cuántica. Como ejemplo, consideremos una onda-partícula cuántica confinada a un círculo, como una ola en un foso circular que rodea un castillo. Una onda sinusoidal en tal “foso cuántico” no puede tener ninguna longitud de onda antigua, porque un número entero de longitudes de onda debe caber alrededor de la circunferencia\(C\),, del foso. Cuanto más grande es este número entero, más corta es la longitud de onda, y una longitud de onda más corta se relaciona con mayor momento y momento angular. Dado que este entero está relacionado con el momento angular, usamos el símbolo\(\ell\) para ello:

\[\begin{equation*} \lambda = C / \ell \end{equation*}\]

El momento angular es

\[\begin{equation*} L = rp . \end{equation*}\]

Aquí,\(r=C/2\pi \), y\(p=h/\lambda=h\ell/C\), entonces

\[\begin{align*} L &= \frac{C}{2\pi}\cdot\frac{h\ell}{C} \\ &= \frac{h}{2\pi}\ell \end{align*}\]

En el ejemplo del foso cuántico, el momento angular se cuantifica en unidades de\(h/2\pi \). Esto hace que sea\(h/2\pi \) un número bastante importante, así que definimos la abreviatura\(\hbar=h/2\pi \). Este símbolo se lee “h-bar”.

De hecho, este es un hecho completamente general en la física cuántica, no solo un hecho sobre el foso cuántico:

Cuantización del momento angular

El momento angular de una partícula debido a su movimiento a través del espacio se cuantifica en unidades de\(\hbar\).

Ejercicio\(\PageIndex{1}\)

¿Cuál es el momento angular de la función de onda que se muestra al inicio de la sección?

Contestar

(respuesta en la parte posterior de la versión PDF del libro)

Tres dimensiones

Nuestra discusión sobre el momento angular cuántico-mecánico se ha limitado hasta ahora a la rotación en un plano, para lo cual simplemente podemos usar signos positivos y negativos para indicar las direcciones de rotación en sentido horario y antihorario. Un átomo de hidrógeno, sin embargo, es inevitablemente tridimensional. El tratamiento clásico del momento angular en tres dimensiones se ha presentado en la sección 4.3; en general, el momento angular de una partícula se define como el producto cruzado vectorial\(\mathbf{r}\times\mathbf{p}\).

Aquí hay un problema básico: el momento angular del electrón en un átomo de hidrógeno depende tanto de su\(\mathbf{r}\) distancia del protón como de su momento\(\mathbf{p}\), por lo que para conocer su momento angular precisamente parecería que necesitaríamos conocer tanto su posición como su impulso simultáneamente con buena precisión. Esto, sin embargo, parece prohibido por el principio de incertidumbre de Heisenberg.

En realidad el principio de incertidumbre sí pone límites a lo que se puede saber sobre el vector de momento angular de una partícula, pero no nos impide conocer su magnitud como un múltiplo entero exacto de\(\hbar\). La razón es que en tres dimensiones, realmente hay tres principios de incertidumbre separados:

\[\begin{align*} \Delta p_x \Delta x &\gtrsim h \\ \Delta p_y \Delta y &\gtrsim h \\ \Delta p_z \Delta z &\gtrsim h \end{align*}\]

b/Conciliar el principio de incertidumbre con la definición de momento angular.

Consideremos ahora una partícula, b /1, que se mueve a lo largo del\(x\) eje en posición\(x\) y con impulso\(p_x\). Puede que no podamos conocer ambos\(x\) y\(p_x\) con precisión ilimitada, pero aún podemos conocer el momento angular de la partícula sobre el origen exactamente: es cero, porque la partícula se aleja directamente del origen.

Supongamos, por otro lado, una partícula se encuentra, b /2, en una posición\(x\) a lo largo del\(x\) eje, y se mueve paralela al\(y\) eje con impulso\(p_y\). Tiene momento angular\(xp_y\) alrededor del\(z\) eje, y nuevamente podemos conocer su momento angular con precisión ilimitada, porque el principio de incertidumbre solo se\(x\) relaciona con\(p_x\) y\(y\) con\(p_y\). No se\(x\) relaciona con\(p_y\).

Como muestran estos ejemplos, el principio de incertidumbre no restringe la precisión de nuestro conocimiento de los momentos angulares tan severamente como podría imaginarse. Sin embargo, sí nos impide conocer los tres componentes de un vector de momento angular simultáneamente. El enunciado más general al respecto es el siguiente teorema, que presentamos sin pruebas:

El vector de momento angular en la física cuántica

Lo más que se puede conocer sobre un vector de momento angular es su magnitud y uno de sus tres componentes vectoriales. Ambos se cuantifican en unidades de\(\hbar\).

c/Una sección transversal de una función de onda de hidrógeno.

El átomo de hidrógeno

Derivar las funciones de onda de los estados del átomo de hidrógeno a partir de los primeros principios sería matemáticamente demasiado complejo para este libro, pero no es difícil entender la lógica detrás de tal función de onda en términos visuales. Considera la función de onda desde el inicio de la sección, la cual se reproduce en la figura c. Aunque la gráfica parece tridimensional, en realidad es solo una representación de la parte de la función ondulada que se encuentra dentro de un plano bidimensional. La tercera dimensión (arriba-abajo) de la gráfica representa el valor de la función de onda en un punto dado, no la tercera dimensión del espacio. El plano elegido para la gráfica es el perpendicular al vector de momento angular.

Cada anillo de picos y valles tiene ocho longitudes de onda dando vueltas en círculo, así que este estado tiene\(L=8\hbar\), es decir, lo etiquetamos\(\ell=8\). La longitud de onda es más corta cerca del centro, y esto tiene sentido porque cuando el electrón está cerca del núcleo tiene una menor energía eléctrica, una mayor energía cinética y un mayor impulso.

Entre cada anillo de picos en esta función de onda hay un círculo nodal, es decir, un círculo en el que la función de onda es cero. La función de onda tridimensional completa tiene esferas nodales: una serie de superficies esféricas anidadas sobre las que es cero. Se llama al número de radios en los que ocurren los nodos\(r=\infty\), incluyendo\(n\), y\(n\) resulta estar estrechamente relacionado con la energía. El estado fundamental tiene\(n=1\) (un solo nodo solo en\(r=\infty\)), y los estados de mayor energía tienen\(n\) valores más altos. Existe una ecuación simple relativa\(n\) a la energía, que discutiremos en la subsección 13.4.4.

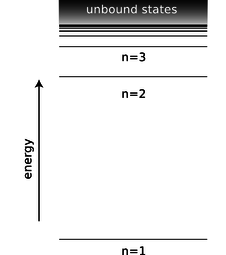
d/La energía de un estado en el átomo de hidrógeno depende únicamente de su número\(n\) cuántico.

Los números\(n\) y\(\ell\), que identifican al estado, se denominan sus números cuánticos. Un estado de un dado\(n\) y\(\ell\) puede orientarse en una variedad de direcciones en el espacio. Podríamos tratar de indicar la orientación usando los tres números cuánticos\(\ell_x=L_x/\hbar\),\(\ell_y=L_y/\hbar\), y\(\ell_z=L_z/\hbar\). Pero ya hemos visto que es imposible conocer los tres simultáneamente. Para dar la descripción más completa posible de un estado, elegimos un eje arbitrario, digamos el\(z\) eje, y etiquetamos el estado según\(n\),\(\ell\), y\(\ell_z\). ⁶

El momento angular requiere movimiento, y el movimiento implica energía cinética. Por lo tanto, no es posible tener una cantidad dada de momento angular sin tener una cierta cantidad de energía cinética también. Dado que la energía se relaciona con el número\(n\) cuántico, esto significa que para un\(n\) valor dado habrá un máximo posible. Resulta que este valor máximo de iguales\(n-1\).

En general, podemos enumerar las posibles combinaciones de números cuánticos de la siguiente manera:

n puede ser igual a 1, 2, 3,...

l puede variar de 0 a n − 1, en pasos de 1

l z puede variar desdeell toell, en pasos de 1

Aplicando estas reglas, tenemos la siguiente lista de estados:

n = 1,	l=0,	l z =0	un estado
n = 2,	l=0,	l z =0	un estado
n = 2,	l=1,	l z =-1, 0 o 1	tres estados

autocomprobación:

Continuar la lista para\(n=3\).

(respuesta en la parte posterior de la versión PDF del libro)

La figura e de la página 882 muestra los estados de menor energía del átomo de hidrógeno. La columna izquierda de gráficos muestra las funciones de onda en el\(x-y\) plano, y la columna derecha muestra la distribución de probabilidad en una representación tridimensional.

e/Los tres estados del átomo de hidrógeno que tienen las energías más bajas.

Preguntas de Discusión

◊ El número cuántico\(n\) se define como el número de radios en los que la función de onda es cero, incluyendo\(r=\infty\). Relacionar esto con las características de las figuras en la página anterior.

◊ Con base en la definición de\(n\), ¿por qué no puede existir tal cosa como un\(n=0\) estado?

◊ Relacionar las características de las gráficas de función de onda en la figura e con las características correspondientes de las imágenes de distribución de probabilidad.

◊ ¿Cómo se puede saber a partir de las gráficas de función de onda en la figura e cuáles tienen qué momento angular?

◊ Criticar la siguiente afirmación incorrecta: “La\(\ell=8\) función de onda en la figura c tiene una longitud de onda más corta en el centro porque en el centro el electrón está en un nivel de energía más alto”.

◊ Discutir las implicaciones del hecho de que la nube de probabilidad en el\(\ell=1\) estado\(n=2\), se divide en dos partes.

Energías de estados en hidrógeno

Historia

La técnica experimental para medir con precisión los niveles de energía de un átomo es la espectroscopia: el estudio del espectro de luz emitida (o absorbida) por el átomo. Sólo los fotones con ciertas energías pueden ser emitidos o absorbidos por un átomo de hidrógeno, por ejemplo, ya que la cantidad de energía ganada o perdida por el átomo debe ser igual a la diferencia de energía entre los estados inicial y final del átomo. La espectroscopia se había convertido en un arte altamente desarrollado varias décadas antes de que Einstein incluso propusiera el fotón, y el espectroscopista suizo Johann Balmer determinó en 1885 que había una ecuación simple que daba todas las longitudes de onda emitidas por el hidrógeno. En términos modernos, pensamos en las longitudes de onda de los fotones simplemente como evidencia indirecta sobre los niveles de energía subyacentes del átomo, y reelaboramos el resultado de Balmer en una ecuación para estos niveles de energía atómica:

\[\begin{equation*} E_n = -\frac{2.2\times10^{-18}\ \text{J}}{n^2} , \end{equation*}\]

Esta energía incluye tanto la energía cinética del electrón como la energía eléctrica. El nivel cero de la escala de energía eléctrica se elige para que sea la energía de un electrón y un protón que están infinitamente separados. Con esta elección, las energías negativas corresponden a los estados unidos y las energías positivas a los no unidos.

¿De dónde\(2.2\times10^{-18}\ \text{J}\) viene el misterioso factor numérico de? En 1913 el teórico danés Niels Bohr se dio cuenta de que era exactamente numéricamente igual a una cierta combinación de constantes físicas fundamentales:

\[\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}\]

donde\(m\) está la masa del electrón, y\(k\) es la constante de fuerza de Coulomb para las fuerzas eléctricas.

Bohr pudo preparar una derivación de esta ecuación basada en la versión incompleta de la física cuántica que se había desarrollado en ese momento, pero su derivación es hoy principalmente de interés histórico. Se supone que el electrón sigue una trayectoria circular, mientras que todo el concepto de un camino para una partícula se considera sin sentido en nuestra versión moderna más completa de la física cuántica. Si bien Bohr fue capaz de producir la ecuación correcta para los niveles de energía, su modelo también dio varios resultados erróneos, como predecir que el átomo sería plano, y que el estado fundamental tendría\(\ell=1\) más que el correcto\(\ell=0\).

Tratamiento aproximado

En lugar de saltar directamente a un tratamiento matemático completo, comenzaremos buscando alguna perspicacia física, lo que conducirá a un argumento aproximado que reproduce correctamente la forma de la ecuación de Bohr.

Un patrón típico de onda estacionaria para el electrón consiste en un área oscilante central rodeada por una región en la que la función de onda se apaga. Como se discute en la subsección 13.3.6, el tipo de patrón oscilante se encuentra típicamente en la región clásicamente permitida, mientras que el desprendimiento ocurre en la región clásicamente prohibida donde el electrón tiene energía cinética insuficiente para penetrar de acuerdo con la física clásica. Usamos el símbolo\(r\) para el radio del límite esférico entre las regiones clásicamente permitidas y clásicamente prohibidas. Clásicamente,\(r\) sería la distancia del protón a la que el electrón tendría que detenerse, darse la vuelta y volver a entrar.

Si\(r\) tuviera el mismo valor para cada patrón de onda estacionaria, entonces esencialmente estaríamos resolviendo el problema de partículas en una caja en tres dimensiones, siendo la caja una cavidad esférica. Considerar los niveles de energía de la partícula en una caja comparados con los del átomo de hidrógeno, f.

f/Los niveles de energía de una partícula en una caja, contrastados con los del átomo de hidrógeno.

Son cualitativamente diferentes. Los niveles de energía de la partícula en una caja se separan cada vez más a medida que aumentamos en energía, y esta característica ni siquiera depende de los detalles de si la caja es bidimensional o tridimensional, o su forma exacta. El motivo de la difusión es que la caja se toma para ser completamente impenetrable, por lo que su tamaño,\(r\), es fijo. Un patrón de onda con\(n\) jorobas tiene una longitud de onda proporcional a\(r/n\), y por lo tanto un impulso proporcional a\(n\), y una energía proporcional a\(n^2\). En el átomo de hidrógeno, sin embargo, la fuerza que mantiene el electrón unido no es una fuerza infinita que se encuentra cuando rebota en una pared, es la fuerza eléctrica atractiva del núcleo. Si ponemos más energía en el electrón, es como lanzar una pelota hacia arriba con una mayor energía —saldrá más lejos antes de volver a bajar. Esto quiere decir que en el átomo de hidrógeno, esperamos aumentar\(r\) a medida que vayamos a estados de mayor energía. Esto tiende a evitar que las longitudes de onda de los estados de alta energía se vuelvan demasiado cortas, reduciendo su energía cinética. El hacinamiento cada vez más cercano de los niveles de energía en el hidrógeno también tiene sentido porque sabemos que hay cierta energía que sería suficiente para hacer que el electrón escape por completo, y por lo tanto la secuencia de estados unidos no puede extenderse por encima de esa energía.

Cuando el electrón está a la distancia máxima permitida clásicamente\(r\) del protón, tiene cero energía cinética. Así, cuando el electrón está a distancia\(r\), su energía es puramente eléctrica:

\[\begin{equation*} E = -\frac{ke^2}{r} \tag{1} \end{equation*}\]

Ahora viene la aproximación. En realidad, la longitud de onda del electrón no puede ser constante en la región clásicamente permitida, pero pretendemos que lo es. Dado que\(n\) es el número de nodos en la función de onda, podemos interpretarlo aproximadamente como el número de longitudes de onda que se ajustan a lo largo del diámetro\(2r\). Ni siquiera estamos intentando una derivación que produzca todos los factores numéricos correctos como 2\(\pi \) y así sucesivamente, así que simplemente hacemos la aproximación

\[\begin{equation*} \lambda \sim \frac{r}{n} . \tag{2} \end{equation*}\]

Finalmente asumimos que la energía cinética típica del electrón está en el mismo orden de magnitud que el valor absoluto de su energía total. (Esto es cierto dentro de un factor de dos para un sistema clásico típico como un planeta en una órbita circular alrededor del sol). Entonces tenemos

\[\begin{align*} \text{absolute}&\text{ value of total energy} \\ &= \frac{ke^2}{r} \notag \\ &\sim K \notag = p^2/2m \notag \\ &= (h/\lambda)^2/2m \notag \\ &\sim h^2n^2/2mr^2 \tag{3} \end{align*}\]

Ahora resolvemos la ecuación\(ke^2/r \sim h^2n^2 / 2mr^2\)\(r\) y desechamos factores numéricos que no podemos esperar haber acertado, cediendo

\[\begin{equation*} r \sim \frac{h^2n^2}{mke^2} .\tag{4} \end{equation*}\]

La conexión\(n=1\) a esta ecuación da\(r=2\) nm, que de hecho está en el orden correcto de magnitud. Finalmente combinamos las ecuaciones (4) y (1) para encontrar

\[\begin{equation*} E \sim -\frac{mk^2e^4}{h^2n^2} , \end{equation*}\]

lo cual es correcto excepto por los factores numéricos que nunca pretendimos encontrar.

Tratamiento exacto del estado fundamental

La prueba general de la ecuación de Bohr para todos los valores de\(n\) está más allá del alcance matemático de este libro, pero es bastante sencillo verificarla para un particular\(n\), especialmente dada una suposición afortunada sobre qué forma funcional probar para la función de onda. La forma que funciona para el estado base es

\[\begin{equation*} \Psi = ue^{-r/a} , \end{equation*}\]

donde\(r=\sqrt{x^2+y^2+z^2}\) está la distancia del electrón desde el protón, y\(u\) prevé la normalización. En lo siguiente, el resultado\(\partial r/\partial x=x/r\) viene muy bien. Computando las derivadas parciales que ocurren en el Laplaciano, obtenemos para el\(x\) término

\[\begin{align*} \frac{\partial\Psi}{\partial x} &= \frac{\partial \Psi}{\partial r} \frac{\partial r}{\partial x} \\ &= -\frac{x}{ar} \Psi \\ \frac{\partial^2\Psi}{\partial x^2} &= -\frac{1}{ar} \Psi -\frac{x}{a}\left(\frac{\partial}{dx}\frac{1}{r}\right)\Psi+ \left( \frac{x}{ar}\right)^2 \Psi\\ &= -\frac{1}{ar} \Psi +\frac{x^2}{ar^3}\Psi+ \left( \frac{x}{ar}\right)^2 \Psi , \text{so} \nabla^2\Psi &= \left( -\frac{2}{ar} + \frac{1}{a^2} \right) \Psi . \end{align*}\]

La ecuación de Schrödinger da

\[\begin{align*} E\cdot\Psi &= -\frac{\hbar^2}{2m}\nabla^2\Psi + U\cdot\Psi \\ &= \frac{\hbar^2}{2m}\left( \frac{2}{ar} - \frac{1}{a^2} \right)\Psi -\frac{ke^2}{r}\cdot\Psi \end{align*}\]

Si requerimos que esta ecuación sostenga para todos\(r\), entonces debemos tener igualdad tanto para los términos de la forma\((\text{constant})\times\Psi\) como para los de la forma\((\text{constant}/r)\times\Psi\). Eso significa

\[\begin{align*} E &= -\frac{\hbar^2}{2ma^2} \\ \text{and} \\ 0 &= \frac{\hbar^2}{mar} -\frac{ke^2}{r} . \end{align*}\]

Estas dos ecuaciones se pueden resolver para las incógnitas\(a\) y\(E\), dando

\[\begin{align*} a &= \frac{\hbar^2}{mke^2} \\ \text{and}\\ E &= -\frac{mk^2e^4}{2\hbar^2} , \end{align*}\]

donde el resultado para la energía concuerda con la ecuación de Bohr para\(n=1\). El cálculo de la constante de normalización\(u\) queda relegado al problema de tarea 36.

Ejercicio\(\PageIndex{1}\)

Hemos verificado que la función\(\Psi = he^{-r/a}\) es una solución a la ecuación de Schrödinger, y sin embargo tiene una torcedura en ella en\(r=0\). ¿Qué está pasando aquí? ¿No discutía antes que las torceduras no son físicas?

Contestar

(respuesta en la parte posterior de la versión PDF del libro)

Ejemplo\(\PageIndex{1}\): Wave phases in the hydrogen molecule

En el ejemplo 16 de la página 861, argumenté que la existencia de la\(\text{H}_2\) molécula podría explicarse esencialmente por un argumento de partícula en una caja: la molécula es una caja más grande que un átomo individual, por lo que la longitud de onda de cada electrón puede ser más larga, su energía cinética menor. Ahora que estamos en posesión de una expresión matemática para la función ondulada del átomo de hidrógeno en su estado fundamental, podemos hacer que este argumento sea un poco más riguroso y detallado. Supongamos que dos átomos de hidrógeno están en una muestra relativamente fría de gas hidrógeno monoatómico. Debido a que el gas es frío, podemos suponer que los átomos están en sus estados terrestres. Ahora supongamos que los dos átomos se acercan entre sí. Haciendo uso nuevamente de la suposición de que el gas está frío, es razonable imaginar que los átomos se acercan lentamente. Ahora los átomos se acercan un poco, pero aún lo suficientemente separados como para que la región entre ellos esté clásicamente prohibida. Cada electrón puede hacer un túnel a través de esta región clásicamente prohibida, pero la probabilidad de tunelización es pequeña. Cada uno se encuentra ahora con, digamos, 99% de probabilidad en su hogar original, pero con 1% de probabilidad en el otro núcleo. Cada electrón se encuentra ahora en un estado que consiste en una superposición del estado fundamental de su propio átomo con el estado fundamental del otro átomo. Hay dos picos en la función de onda superpuesta, pero uno es un pico mucho más grande que el otro.

Ahora surge una pregunta interesante. ¿Cuáles son las fases relativas de los dos electrones? Como se discute en la página 855, la fase absoluta de la función de onda de un electrón no es realmente un concepto significativo. Supongamos que el átomo A contiene electrón Alice, y B electrón Bob. Justo antes de la colisión, Alice pudo haberse preguntado: “¿Mi fase es positiva en este momento, o es negativa? Pero claro que no debería hacerme preguntas tan tontas”, agrega tímidamente.

g/Ejemplo 23.

Pero las fases relativas están bien definidas. A medida que los dos átomos se acercan cada vez más, la probabilidad de tunelización aumenta, y eventualmente se vuelve tan alta que cada electrón está gastando esencialmente el 50% de su tiempo en cada átomo. Ahora es razonable imaginar que cualquiera de las dos posibilidades podría obtener. La función de onda de Alice podría verse como g /1, con los dos picos en fase entre sí, o podría parecer g /2, con fases opuestas. Debido a que las fases relativas de las funciones de onda están bien definidas, los estados 1 y 2 son físicamente distinguibles. En particular, la energía cinética del estado 2 es mucho mayor; en términos generales, es como el patrón de onda de dos jorobas de la partícula en una caja, a diferencia de 1, que se parece aproximadamente al patrón de una joroba con una longitud de onda mucho más larga. No sólo eso, sino que un electrón en estado 1 tiene una gran probabilidad de ser encontrado en la región central, donde tiene una gran energía eléctrica negativa debido a su interacción con ambos protones. El Estado 2, en cambio, tiene una baja probabilidad de existir en esa región. Así, el estado 1 representa la verdadera función de onda del estado fundamental de la\(\text{H}_2\) molécula, y poner tanto a Alice como a Bob en ese estado da como resultado una energía menor que su energía total cuando se separan, por lo que la molécula se une, y no se separará espontáneamente.

El estado g/3, por otro lado, no es físicamente distinguible de g /2, ni g /4 de g /1. Alice puede decirle a Bob: “¿No es maravilloso que estemos en el estado 1 o 4? Me encanta estar estable así”. Pero sabe que no tiene sentido preguntarse en un momento dado en qué estado se encuentra, 1 o 4.

Solución

Agrega texto aquí.

Preguntas de Discusión

• Los estados de hidrógeno con\(n\) más de aproximadamente 10 nunca se observan en el sol. ¿Por qué podría ser esto?
• Croquis gráficos de\(r\) y\(E\) versus\(n\) para el hidrógeno, y comparar con gráficas análogas para la partícula unidimensional en una caja.

Espín de electrones

Es desconcertante para el jugador novato de ping-pong encontrarse por primera vez con un jugador más hábil que pueda poner giro a la pelota. A pesar de que no se puede ver que la pelota está girando, se nota que algo está pasando por la forma en que interactúa con otros objetos en su entorno. De la misma manera, podemos decir por la forma en que los electrones interactúan con otras cosas que tienen un giro intrínseco propio. Los experimentos muestran que incluso cuando un electrón no se mueve a través del espacio, todavía tiene un momento angular que asciende a\(\hbar/2\).

h/La parte superior tiene momento angular tanto por el movimiento de su centro de masa a través del espacio como por su rotación interna. El espín electrónico es aproximadamente análogo al espín intrínseco de la parte superior.

Esto puede parecer paradójico porque el foso cuántico, por ejemplo, dio solo momentos angulares que eran múltiplos enteros de\(\hbar\), no medias unidades, y afirmé que el momento angular siempre se cuantificó en unidades de\(\hbar\), no solo en el caso del foso cuántico. Toda esa discusión, sin embargo, asumió que el momento angular vendría del movimiento de una partícula a través del espacio. El momento\(\hbar/2\) angular del electrón es simplemente una propiedad de la partícula, como su carga o su masa. No tiene nada que ver con si el electrón se mueve o no, y no proviene de ningún movimiento interno dentro del electrón. Nadie ha logrado nunca encontrar ninguna estructura interna dentro del electrón, e incluso si hubiera una estructura interna, sería matemáticamente imposible que resultara en una media unidad de momento angular.

Simplemente tenemos que aceptar este momento\(\hbar/2\) angular, llamado el “giro” del electrón — la Madre Naturaleza nos frota la nariz en él como un hecho observado.

Los protones y neutrones tienen el mismo\(\hbar/2\) giro, mientras que los fotones tienen un giro intrínseco de\(\hbar\). En general, los espines semienteros son típicos de las partículas de material. Se encuentran valores integrales para las partículas que portan fuerzas: los fotones, que encarnan los campos eléctricos y magnéticos de fuerza, así como los mensajeros más exóticos de las fuerzas nucleares y gravitacionales.

Como fue el caso del momento angular ordinario, podemos describir el momento angular de giro en términos de su magnitud, y su componente a lo largo de un eje dado. Escribimos\(s\) y\(s_z\) para estas cantidades, expresadas en unidades de\(\hbar\), así que un electrón tiene\(s=1/2\) y\(s_z=+1/2\) o\(-1/2\).

Teniendo en cuenta el espín electrónico, necesitamos un total de cuatro números cuánticos para etiquetar un estado de un electrón en el átomo de hidrógeno:\(n\),\(\ell\),\(\ell_z\), y\(s_z\). (Omitimos\(s\) porque siempre tiene el mismo valor.) Los símbolos e incluyen solo el momento angular que tiene el electrón porque se mueve a través del espacio, no su momento angular de giro. La disponibilidad de dos posibles estados de espín del electrón conduce a una duplicación de los números de estados:

n = 1,	l=0,	l z =0,	s z = + 1/2 o − 1/2	dos estados
n = 2,	l=0,	l z =0,	s z = + 1/2 o − 1/2	dos estados
n = 2,	l=1,	l z =-1, 0 o 1	s z = + 1/2 o − 1/2	seis estados

Una nota sobre la notación

Desafortunadamente, hay dos sistemas inconsistentes de notación para los números cuánticos que hemos estado discutiendo. La notación que he estado usando es la que se usa en física nuclear, pero hay otra diferente que se usa en física atómica.

física nuclear	física atómica
n	mismo
l	mismo
l x	sin notación
l y	sin notación
l z	m
s = 1/2	sin notación (a veces σ)
s x	sin notación
s y	sin notación
s z	s

la notación de física nuclear es más lógica (no darle un estatus especial al\(z\) eje) y más memorable (en\(\ell_z\) lugar de lo oscuro\(m\)), razón por la cual la uso consistentemente en este libro, aunque casi todas las aplicaciones que consideraremos son atómicas.

Además, estamos gravados con las siguientes etiquetas de letras derivadas históricamente, que merecen ser eliminadas en favor de las numéricas más simples:

l=0	l=1	l=2	l=3
s	p	d	f

n = 1	n = 2	n = 3	n = 4	n = 5	n = 6	n = 7
K	L	M	N	O	P	Q

Las etiquetas spdf se utilizan tanto en la física nuclear ⁷ como en la atómica, mientras que las letras KLMNOPQ se utilizan únicamente para referirse a estados de electrones.

Y por último, hay una pieza de notación que es buena y útil, pero que simplemente no he mencionado todavía. El vector\(\mathbf{j}=\v c{\ell}+\mathbf{s}\) representa el momento angular total de una partícula en unidades de\(\hbar\), incluyendo partes orbitales y espín. Este número cuántico resulta ser muy útil en la física nuclear, porque las fuerzas nucleares tienden a intercambiar momento angular orbital y giro, por lo que un nivel de energía dado a menudo contiene una mezcla de\(\ell\) y\(s\) valores, mientras que permanece bastante puro en términos de\(j\).

13.4.6 Átomos con más de un electrón

¿Qué pasa con otros átomos además del hidrógeno? Parecería que las cosas se volverían mucho más complejas con la adición de un segundo electrón. Un átomo de hidrógeno sólo tiene una partícula que se mueve mucho, ya que el núcleo es tan pesado y casi inmóvil. El helio, con dos, sería un desastre. En lugar de una función de onda cuyo cuadrado nos dice la probabilidad de encontrar un solo electrón en cualquier ubicación dada en el espacio, un átomo de helio necesitaría tener una función de onda cuyo cuadrado nos indicaría la probabilidad de encontrar dos electrones en cualquier combinación dada de puntos. ¡Ay! Además, tendríamos la complicación extra de la interacción eléctrica entre los dos electrones, en lugar de poder imaginar todo en términos de un electrón que se mueve en un campo estático de fuerza creado solo por el núcleo.

A pesar de todo esto, resulta que podemos obtener una descripción sorprendentemente buena de muchos átomos de electrones simplemente asumiendo que los electrones pueden ocupar los mismos patrones de onda estacionaria que existen en un átomo de hidrógeno. El estado fundamental del helio, por ejemplo, tendría ambos electrones en estados que son muy similares a los\(n=1\) estados del hidrógeno. El segundo estado de menor energía del helio tendría un electrón en un\(n=1\) estado, y el otro en un\(n=2\) estado. Los espectros relativamente complejos de elementos más pesados que el hidrógeno pueden entenderse como derivados del gran número de posibles combinaciones de estados para los electrones.

Algo sorprendente sucede, sin embargo, con el litio, el átomo de tres electrones. Esperaríamos que el estado fundamental de este átomo sea uno en el que los tres electrones se asienten en\(n=1\) estados. Lo que realmente sucede es que dos electrones van a\(n=1\) estados, pero el tercero se queda arriba en un\(n=2\) estado. Esto es consecuencia de un nuevo principio de la física:

El principio de exclusión de Pauli

Sólo un electrón puede ocupar un estado dado.

Hay dos\(n=1\) estados, uno con\(s_z=+1/2\) y otro con\(s_z=-1/2\), pero no hay un tercer\(n=1\) estado para que ocupe el tercer electrón del litio, por lo que se ve obligado a entrar en un\(n=2\) estado.

Se puede demostrar matemáticamente que el principio de exclusión de Pauli se aplica a cualquier tipo de partícula que tenga espín semientero. Así dos neutrones nunca podrán ocupar el mismo estado, e igualmente para dos protones. Los fotones, sin embargo, son inmunes al principio de exclusión porque su espín es un número entero.

Derivar la tabla periódica

i/El inicio de la tabla periódica.

Ahora podemos dar cuenta de la estructura de la tabla periódica, que le pareció tan misteriosa incluso a su inventor Mendeleev. La primera fila consiste en átomos con electrones solo en los\(n=1\) estados:

H	1 electrón en un estado n = 1
Él	2 electrones en los dos estados n = 1

La siguiente fila se construye llenando los niveles\(n=2\) de energía:

Li	2 electrones en n = 1 estados, 1 electrón en un estado n = 2
Be	2 electrones en n = 1 estados, 2 electrones en n = 2 estados
...
O	2 electrones en n = 1 estados, 6 electrones en n = 2 estados
F	2 electrones en n = 1 estados, 7 electrones en n = 2 estados
Ne	2 electrones en n = 1 estados, 8 electrones en n = 2 estados

En la tercera fila empezamos en los\(n=3\) niveles:

Na	2 electrones en n = 1 estados, 8 electrones en n = 2 estados, 1 electrón en un estado n = 3

Ahora podemos ver un vínculo lógico entre el llenado de los niveles de energía y la estructura de la tabla periódica. La columna 0, por ejemplo, consiste en átomos con el número correcto de electrones para llenar todos los estados disponibles hasta un cierto valor de\(n\). La columna I contiene átomos como el litio que tienen sólo un electrón más que eso.

Esto demuestra que las columnas se relacionan con el llenado de los niveles de energía, pero ¿por qué eso tiene algo que ver con la química? ¿Por qué, por ejemplo, los elementos de las columnas I y VII son peligrosamente reactivos?

j/El hidrógeno es altamente reactivo.

Consideremos, por ejemplo, el elemento sodio (Na), que es tan reactivo que puede estallar en llamas cuando se expone al aire. El electrón en el\(n=3\) estado tiene una energía inusualmente alta. Si dejamos que un átomo de sodio entre en contacto con un átomo de oxígeno, la energía puede liberarse transfiriendo el\(n=3\) electrón del sodio a uno de los\(n=2\) estados vacantes de menor energía en el oxígeno. Esta energía se transforma en calor. Cualquier átomo en la columna I es altamente reactivo por la misma razón: puede liberar energía regalando el electrón que tiene una energía inusualmente alta.

La columna VII es espectacularmente reactiva por la razón opuesta: estos átomos tienen una sola vacante en un estado de baja energía, por lo que la energía se libera cuando estos átomos roban un electrón de otro átomo.

Podría parecer que estos argumentos solo explicarían reacciones de átomos que se encuentran en distintas filas de la tabla periódica, porque solo en estas reacciones puede un electrón transferido pasar de un\(n\) estado superior a un\(n\) estado inferior. Esto es incorrecto. Un\(n=2\) electrón en flúor (F), por ejemplo, tendría una energía diferente a la de un\(n=2\) electrón en litio (Li), debido al diferente número de protones y electrones con los que interactúa. En términos generales, el\(n=2\) electrón en el flúor está más unido (menor en energía) debido al mayor número de protones que lo atraen. El efecto del aumento del número de protones atrayentes solo se contrarresta parcialmente por el aumento en el número de electrones repelentes, porque las fuerzas ejercidas sobre un electrón por los otros electrones están en muchas direcciones diferentes y cancelan parcialmente.

Colaboradores y Atribuciones

Template:ContribCrowell