14.6: Problemas

1. Si una sustancia radiactiva tiene una vida media de un año, ¿significa esto que se desintegrará por completo después de dos años? Explique.

2. ¿Cuál es la probabilidad de rodar un par de dados y obtener “ojos de serpiente”, es decir, ambos dados vienen con unos?

3. Se ha eliminado el problema 3.

4. Se ha eliminado el problema 4.

5. Consulte la distribución de probabilidad para las alturas de las personas en la figura f en la página 828.
(a) Demostrar que la gráfica está normalizada correctamente.
b) Estimar la fracción de la población que tiene alturas entre 140 y 150 cm. (consulta de respuesta disponible en lightandmatter.com)

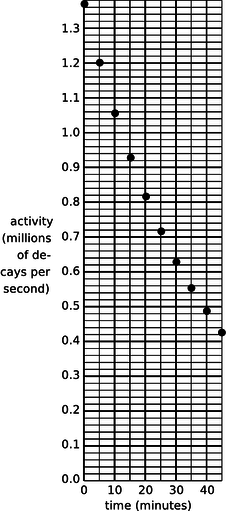
a/Problema 6.

6. a) Un físico nuclear está estudiando una reacción nuclear provocada en un experimento con acelerador, con un haz de iones del acelerador golpeando una delgada lámina metálica y provocando reacciones nucleares cuando un núcleo de uno de los iones del haz choca con uno de los núcleos del objetivo. Después de que el experimento ha estado funcionando durante algunas horas, se han producido unos pocos miles de millones de átomos radiactivos, incrustados en el objetivo. Ella no sabe qué núcleos se están produciendo, pero sospecha que son un isótopo de algún elemento pesado como Pb, Bi, Fr o U. Después de uno de esos experimentos, saca la lámina objetivo del acelerador, la pega frente a un detector, mide la actividad cada 5 min y hace una gráfica (figura). Los isótopos que cree que pueden haber sido producidos son:

isótopo	vida media (minutos)
^211 Pb	36.1
^214 Pb	26.8
214 Bi	19.7
^223 Fr	21.8
^239 U	23.5

¿Cuál es?
b) Habiendo decidido que las condiciones experimentales originales producían un isótopo específico, ahora intenta utilizar haces de iones que viajan a varias velocidades diferentes, lo que puede provocar reacciones diferentes. La siguiente tabla da la actividad de la diana 10, 20 y 30 minutos después del final del experimento, para tres velocidades de iones diferentes.

	actividad (millones de decais/s) tras...
	10 min	20 min	30 min
primera velocidad de iones	1.933	0.832	0.382
segunda velocidad de iones	1.200	0.545	0.248
tercera velocidad de iones	7.211	1.296	0.248

Dado que se está contando un número tan grande de decae, supongamos que los datos sólo son inexactos debido al redondeo al anotar la tabla. ¿Cuáles son consistentes con la producción de un solo isótopo, y que implican que se estaba creando más de un isótopo?

7. Diseñar un método para probar experimentalmente la hipótesis de que la oportunidad de un jugador de ganar a los dados es independiente de su récord anterior de victorias y derrotas. Si no invocas la definición de independencia estadística, entonces no has propuesto una prueba.

8. Una persona con los ojos vendados dispara un arma de fuego contra un objetivo circular de radio\(b\), y se le permite continuar disparando hasta que un disparo realmente lo golpea. Cualquier parte del objetivo es igualmente probable que sea golpeada. Medimos la distancia aleatoria\(r\) desde el centro del círculo hasta donde entró la bala.
(a) Demostrar que la distribución de probabilidad de\(r\) debe ser de la forma\(D(r)=kr\), donde\(k\) hay alguna constante. (Claro que tenemos\(D(r)=0\) para\(r>b\).)
b) Determinar\(k\) requiriendo\(D\) estar debidamente normalizado. (consulta de respuesta disponible en lightandmatter.com)

(c) Encuentra el valor promedio de\(r\). (consulta de respuesta disponible en lightandmatter.com)

(d) Interpretando tu resultado de la parte c, ¿cómo se compara con\(b/2\)? ¿Tiene sentido esto? Explique.

9. Se nos dan algunos átomos de cierto isótopo radiactivo, con vida media\(t_{1/2}\). Escogemos un átomo al azar, y lo observamos durante una vida media, comenzando en el tiempo cero. Si decae durante ese período de semivida, registramos el\(t\) momento en que ocurrió la decadencia. Si no es así, reiniciamos nuestro reloj a cero y seguimos intentándolo hasta conseguir un átomo que coopere. El resultado final es un tiempo\(0\le t\le t_{1/2}\), con una distribución que parece la curva de decaimiento exponencial habitual, pero con su cola cortada.
a) Encontrar la distribución\(D(t)\), con la debida normalización. (consulta de respuesta disponible en lightandmatter.com)

(b) Encuentra el valor promedio de\(t\). (consulta de respuesta disponible en lightandmatter.com)

(c) Interpretando tu resultado de la parte b, ¿cómo se compara con\(t_{1/2}/2\)? ¿Tiene sentido esto? Explique.

10. La velocidad,\(v\), de un átomo en un gas ideal tiene una distribución de probabilidad de la forma\(D(v) = bve^{-cv^2}\), donde\(0\le v \lt \infty\),\(c\) se relaciona con la temperatura, y\(b\) está determinada por la normalización.
a) Esbozar la distribución.
(b) Encontrar\(b\) en términos de\(c\). (consulta de respuesta disponible en lightandmatter.com)

(c) Encuentra la velocidad promedio en términos de\(c\), eliminando\(b\). (No trates de hacer la integral indefinida, porque no se puede hacer en forma cerrada. La integral definida relevante se puede encontrar en tablas o se puede hacer con software de computadora.) (consulta de respuesta disponible en lightandmatter.com)

11. Todo el helio en la tierra proviene de la desintegración de elementos radiactivos pesados de origen natural como el uranio. Cada partícula alfa que se emite termina reclamando dos electrones, lo que la convierte en un átomo de helio. Si el\(^{238}\text{U}\) átomo original está en roca sólida (a diferencia de las regiones fundidas de la tierra), los átomos de He son incapaces de difundirse fuera de la roca. Este problema implica fechar una roca utilizando las propiedades de desintegración conocidas del uranio 238. Supongamos que un geólogo encuentra una muestra de lava endurecida, la derrite en un horno y encuentra que contiene 1230 mg de uranio y 2.3 mg de helio. \(^{238}\text{U}\)decae por emisión alfa, con una vida media de\(4.5\times10^9\) años. La cadena posterior de decae alfa y electrón (beta) implica semividas mucho más cortas y termina en el núcleo estable\(^{206}\text{Pb}\). Casi todo el uranio natural es\(^{238}\text{U}\), y la composición química de esta roca indica que no hubo cadenas de desintegración involucradas aparte de la de\(^{238}\text{U}\).
a) ¿Cuántos alfas se emiten por cadena de decaimiento? [Pista: Utilice la conservación de la masa.]
b) ¿Cuántos electrones se emiten por cadena de decaimiento? [Pista: Usar conservación de carga.]
(c) ¿Cuánto tiempo ha pasado desde que la lava se endureció originalmente? (consulta de respuesta disponible en lightandmatter.com)

12. Cuando la luz se refleja desde un espejo, tal vez solo regresa el 80% de la energía. Se podría tratar de explicar esto de dos maneras diferentes: (1) 80% de los fotones se reflejan, o (2) todos los fotones se reflejan, pero cada uno pierde 20% de su energía. A partir de tus conocimientos cotidianos sobre los espejos, ¿cómo puedes saber qué interpretación es la correcta? [Basado en un problema de PSSC Physics.]

13. Supongamos que queremos construir un sensor de luz electrónico utilizando un aparato como el descrito en la sección sobre el efecto fotoeléctrico. ¿Cómo dependería su capacidad para detectar diferentes partes del espectro del tipo de metal utilizado en las placas del condensador?

14. El efecto fotoeléctrico puede ocurrir no solo para los cátodos metálicos sino para cualquier sustancia, incluido el tejido vivo. La ionización de moléculas de ADN puede causar cáncer o defectos congénitos. Si la energía requerida para ionizar el ADN es del mismo orden de magnitud que la energía requerida para producir el efecto fotoeléctrico en un metal, ¿cuál de los siguientes tipos de ondas electromagnéticas podría representar tal peligro? Explique.

Ondas de 60 Hz desde líneas eléctricas

Radio FM de 100 MHz

microondas de un horno de microondas

luz visible

luz ultravioleta

radiografías

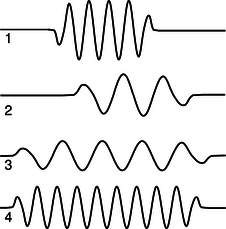
b/Problema 15.

15. (a) Ordene por rango los fotones según sus longitudes de onda, frecuencias y energías. Si dos son iguales, dígalo. Explique todas sus respuestas.
b) El fotón 3 fue emitido por un átomo de xenón que iba de su segundo estado de energía más baja a su estado de menor energía. ¿Cuáles de los fotones 1, 2 y 4 son capaces de excitar un átomo de xenón desde su estado de energía más baja a su segundo estado de energía más baja? Explique.

c/Problema 16.

16. ¿Qué cifra podría ser un electrón acelerando a medida que se mueve hacia la derecha? Explique.

17. El haz de un retroproyector de 100-W cubre un área de\(1\ \text{m}\times1\ \text{m}\) cuando golpea la pantalla a 3 m de distancia. Estimar el número de fotones que están en vuelo en un momento dado. (Dado que esto es sólo una estimación, podemos ignorar el hecho de que el haz no es paralelo). (consulta de respuesta disponible en lightandmatter.com)

18. En el efecto fotoeléctrico, los electrones se observan prácticamente sin retardo de tiempo (\(\sim10\)ns), incluso cuando la fuente de luz es muy débil. (Sin embargo, una fuente de luz débil solo produce un pequeño número de electrones expulsados). El propósito de este problema es mostrar que la falta de un retraso significativo en el tiempo contradice la teoría clásica de las ondas de la luz, por lo que a lo largo de este problema debes ponerte en la piel de un físico clásico y fingir que no sabes nada de fotones. En ese momento, se pensó que el electrón podría tener un radio del orden de\(10^{-15}\) m. (Experimentos recientes han demostrado que si el electrón tiene algún tamaño finito, es mucho más pequeño).
a) Estimar la potencia que sería absorbida por un solo electrón en un haz de luz con una intensidad de 1\(\text{mW}/\text{m}^2\). (answer check available at lightandmatter.com)
(b) La energía,\(E_s\), requerida para que el electrón escape a través de la superficie del cátodo es del orden de\(10^{-19}\) J. Encuentra cuánto tiempo tardaría el electrón en absorber esta cantidad de energía, y explica por qué tu resultado constituye fuerte evidencia de que hay algo mal con la teoría clásica. (consulta de respuesta disponible en lightandmatter.com)

19. En una televisión, supongamos que los electrones se aceleran desde el reposo a través de una diferencia de voltaje de\(10^4\) V. ¿Cuál es su longitud de onda final? (consulta de respuesta disponible en lightandmatter.com)

20. Utilice el principio de incertidumbre de Heisenberg para estimar la velocidad mínima de un protón o neutrón en un\(^{208}\text{Pb}\) núcleo, que tiene un diámetro de aproximadamente 13 fm (1 fm=\(10^{-15}\) m). Asumir que la velocidad es no relativista, y luego verificar al final si esta suposición estaba justificada. (consulta de respuesta disponible en lightandmatter.com)

21. Encuentra la energía de una partícula en una caja unidimensional de longitud\(L\), expresando tu resultado en términos de\(L\), la masa de la partícula\(m\), el número de picos y valles\(n\) en la función de onda, y constantes fundamentales. (consulta de respuesta disponible en lightandmatter.com)

22. Un electrón libre que contribuye a la corriente en un material óhmico normalmente tiene una velocidad de\(10^5\) m/s (mucho mayor que la velocidad de deriva).
a) Estimar su longitud de onda de Broglie, en nm. (verificación de respuesta disponible en lightandmatter.com)
(b) Si un chip de memoria de computadora contiene circuitos\(10^8\) eléctricos en un\(\text{cm}^2\) área 1, estime el tamaño lineal, en nm, de uno de esos circuitos. (verificación de respuesta disponible en lightandmatter.com)
(c) Basado en sus respuestas de las partes a y b, ¿un ingeniero eléctrico que diseña un chip de este tipo necesita preocuparse por los efectos de onda como la difracción?
d) Estimar el número máximo de circuitos eléctricos que pueden caber en un chip de\(\text{cm}^2\) computadora 1 antes de que los efectos cuántico-mecánicos sean importantes.

23. En la mecánica clásica, una energía de interacción de la forma\(U(x)=\frac{1}{2}kx^2\) da un oscilador armónico: la partícula se mueve hacia adelante y hacia atrás a una frecuencia\(\omega=\sqrt{k/m}\). Esta forma para\(U(x)\) es a menudo una buena aproximación para un átomo individual en un sólido, que puede vibrar alrededor de su posición de equilibrio en\(x=0\). (Por simplicidad, restringimos nuestro tratamiento a una dimensión, y tratamos al átomo como una sola partícula más que como un núcleo rodeado de electrones). El átomo, sin embargo, debe tratarse cuánto-mecánicamente, no clásicamente. Tendrá una función de onda. Esperamos que esta función de onda tenga uno o más picos en la región clásicamente permitida, y esperamos que siga en las regiones clásicamente prohibidas a derecha e izquierda. Dado que la forma de\(U(x)\) es una parábola, no una serie de escalones planos como en la figura m de la página 869, la parte ondulada en el medio no será una onda sinusoidal, y las colas no serán exponenciales.
(a) Demostrar que existe una solución a la ecuación de Schrödinger de la forma

\[\begin{equation*} \Psi(x)=e^{-bx^2} , \end{equation*}\]

y\(b\) relacionarse con\(k\),\(m\), y\(\hbar\). Para ello, calcule la segunda derivada, conecte el resultado a la ecuación de Schrödinger, y luego encuentre qué valor de\(b\) haría válida la ecuación para todos los valores de\(x\). Esta función de onda resulta ser el estado fundamental. Tenga en cuenta que esta función de onda no está normalizada correctamente, no se preocupe por eso. (verificación de respuesta disponible en lightandmatter.com)
(b) Dibuja un gráfico que muestre cómo es esta función de onda.
(c) Vamos a interpretar\(b\). Si cambiaste\(b\), ¿cómo se vería diferente la función de onda? Demostrar dibujando dos gráficas, una para un valor menor de\(b\), y otra para un valor mayor.
d) Hacer\(k\) mayor significa hacer que el átomo esté más unido. Matemáticamente, ¿qué pasa con el valor de\(b\) en tu resultado de la parte a si haces\(k\) mayor? ¿Esto tiene sentido físicamente cuando se compara con la parte c?

24. (a) Una escala de distancia se muestra debajo de las funciones de onda y densidades de probabilidad ilustradas en la figura e de la página 882. Compare esto con la estimación de orden de magnitud derivada en la subsección 13.4.4 para el radio\(r\) en el que la función de onda comienza a desprenderse. ¿Fue la estimación en el orden correcto de magnitud?
(b) Aunque normalmente decimos que la luna orbita la tierra, en realidad ambas orbitan alrededor de su centro de masa común, que está por debajo de la superficie terrestre pero no en su centro. Lo mismo ocurre con el átomo de hidrógeno. ¿El centro de masa se encuentra dentro del protón, o fuera de él?

d/Problema 25.

25. La figura muestra ocho de las posibles formas en que un electrón en un átomo de hidrógeno podría caer de un estado de mayor energía a un estado de menor energía, liberando la diferencia de energía como fotón. De estas ocho transiciones, solo D, E y F producen fotones con longitudes de onda en el espectro visible.
a) ¿Cuál de las transiciones visibles estaría más cerca del extremo violeta del espectro y cuál estaría más cerca del extremo rojo? Explique.
(b) ¿En qué parte del espectro electromagnético estarían los fotones de las transiciones A, B y C? ¿Qué pasa con G y H? Explique.
c) ¿Existe un límite superior en las longitudes de onda que podría emitir un átomo de hidrógeno que va de un estado unido a otro estado enlazado? ¿Hay un límite inferior? Explique.

26. Encuentra una ecuación para la longitud de onda del fotón emitido cuando el electrón en un átomo de hidrógeno hace una transición de nivel de energía\(n_1\) a nivel\(n_2\). (consulta de respuesta disponible en lightandmatter.com)

27. Estimar el momento angular de una básquetbol giratorio, en unidades de\(\hbar\). Explique cómo este resultado se relaciona con el principio de correspondencia.

28. Supongamos que la energía cinética de un electrón el\(n=1\) estado de un átomo de hidrógeno está en el mismo orden de magnitud que el valor absoluto de su energía total, y estime una velocidad típica a la que se estaría moviendo. (Realmente no puede tener una sola velocidad definida, porque su energía cinética y de interacción se compensan a diferentes distancias del protón, pero esto es solo una estimación aproximada de una velocidad típica). Con base en esta velocidad, ¿estábamos justificados al suponer que el electrón podría describirse de manera no relativista?

29. Antes de la teoría cuántica, los experimentalistas señalaron que en muchos casos, encontrarían tres líneas en el espectro del mismo átomo que satisfacían la siguiente regla misteriosa:\(1/\lambda_1=1/\lambda_2+1/\lambda_3\). Explique por qué ocurriría esto. No utilice el razonamiento que sólo funciona para el hidrógeno — tales combinaciones ocurren en los espectros de todos los elementos. [Pista: Reafirmar la ecuación en términos de las energías de los fotones.]

30. La función de onda del electrón en el estado fundamental de un átomo de hidrógeno es

\[\begin{equation*} \Psi = \pi^{-1/2} a^{-3/2} e^{-r/a} , \end{equation*}\]

donde\(r\) está la distancia desde el protón, y\(a=5.3\times10^{-11}\) m es una constante que establece el tamaño de la ola.
(a) Calcular simbólicamente, sin enchufar números, la probabilidad de que en cualquier momento, el electrón se encuentre dentro del protón. Supongamos que el protón es una esfera con un radio de\(b=0.5\) fm. [Pista: ¿Importa si conectas\(r=0\) o\(r=b\) entras en la ecuación para la función de onda?] (verificación de respuesta disponible en lightandmatter.com)
(b) Calcular la probabilidad numéricamente. (answer check available at lightandmatter.com)
(c) Basado en la ecuación para la función de onda, ¿es válido pensar que un átomo de hidrógeno tiene un tamaño finito? ¿\(a\)Se puede interpretar como el tamaño del átomo, más allá del cual no hay nada? ¿O hay algún límite sobre qué tan lejos puede estar el electrón del protón?

31. Utilizar el razonamiento físico para explicar cómo la ecuación para los niveles de energía del hidrógeno,

\[\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}\]

debe generalizarse al caso de un átomo con número atómico al\(Z\) que se le hayan quitado todos sus electrones excepto uno.

32. Un muón es una partícula subatómica que actúa exactamente como un electrón excepto que su masa es 207 veces mayor. Los muones pueden ser creados por rayos cósmicos, y puede suceder que uno de los electrones de un átomo sea desplazado por un muón, formando un átomo muónico. Si esto le sucede a un átomo de hidrógeno, el sistema resultante consiste simplemente en un protón más un muón.
a) Con base en los resultados de la sección 13.4.4, ¿cómo se compararía el tamaño de un átomo de hidrógeno muónico en su estado fundamental con el tamaño del átomo normal?
(b) Si estuvieras buscando átomos muónicos en el sol o en la atmósfera terrestre por espectroscopía, ¿en qué parte del espectro electromagnético esperarías encontrar las líneas de absorción?

33. Un fotón choca con un electrón y rebota de la colisión a 180 grados, es decir, retrocediendo por el camino por el que vino. El fotón de rebote tiene una energía diferente, y por lo tanto una frecuencia y longitud de onda diferentes. Demostrar que, con base en la conservación de la energía y el impulso, la diferencia entre las longitudes de onda inicial y final del fotón debe ser\(2h/mc\), donde\(m\) está la masa del electrón. La verificación experimental de este tipo de comportamiento de “bola de alberca” por Arthur Compton en 1923 se tomó como prueba definitiva de la naturaleza de partículas de la luz. Tenga en cuenta que no estamos haciendo ninguna aproximación no relativista. Para mantener el álgebra simple, debes usar unidades naturales —de hecho, es una buena idea usar unidades pares-más-naturales-que-naturales, en las que tenemos no solo\(c=1\) sino también\(h=1\), y\(m=1\) para la masa del electrón. También probablemente querrás usar la relación relativista\(E^2-p^2=m^2\), que se convierte\(E^2-p^2=1\) para la energía y el impulso del electrón en estas unidades.

34. Generalizar el resultado del problema 33 al caso donde el fotón rebota en un ángulo distinto de 180° con respecto a su dirección inicial de movimiento.

35. En la página 869 derivamos una expresión para la probabilidad de que una partícula haga un túnel a través de una barrera rectangular, es decir, una región en la que la energía de interacción\(U(x)\) tiene una gráfica que parece un rectángulo. Generalizar esto a una barrera de cualquier forma. [Consejos: Primero intente generalizar a dos barreras rectangulares seguidas, y luego use una serie de barreras rectangulares para aproximarse a la curva real de una función arbitraria\(U(x)\). Tenga en cuenta que el ancho y la altura de la barrera en la ecuación original ocurren de tal manera que lo único que importa es el área bajo la\(x\) curva\(U\) -versus-. Demostrar que esto sigue siendo cierto para una serie de barreras rectangulares, y generalizar utilizando una integral.] Si hubieras hecho este cálculo en la década de 1930 podrías haberte convertido en un famoso físico.

36. Demostrar que la función de onda dada en el problema 30 está normalizada correctamente.

37. Mostrar que una función de onda de la forma\(\Psi = e^{by} \sin ax \) es una posible solución de la ecuación de Schrödinger en dos dimensiones, con un potencial constante. ¿Podemos decir si se aplicaría a una región clásicamente permitida, o a una clásicamente prohibida?

38. Encuentre los niveles de energía de una partícula en una caja rectangular tridimensional con lados de longitud\(a\),\(b\), y\(c\). (consulta de respuesta disponible en lightandmatter.com)

39. Americio-241 es un isótopo artificial utilizado en detectores de humo. Se somete a desintegración alfa, con una vida media de 432 años. Como se discutió en el ejemplo 18 de la página 870, la desintegración alfa puede entenderse como un proceso de tunelización, y aunque la barrera no es de forma rectangular, la ecuación para la probabilidad de tunelización en la página 870 puede seguir siendo utilizada como una guía aproximada de nuestro pensamiento. Para americio-241, la probabilidad de tunelización es de aproximadamente\(1\times10^{-29}\). Supongamos que este núcleo iba a descomponerse emitiendo un núcleo de tritio (helio-3) en lugar de una partícula alfa (helio-4). Estimar la probabilidad de tunelización relevante, asumiendo que la energía total\(E\) sigue siendo la misma. Esta mayor probabilidad es contraria a la observación empírica de que no se observa que este núcleo se descompone por emisión de tritio con alguna probabilidad significativa, y en general la emisión de tritio es casi desconocida en la naturaleza; esto se debe principalmente a que el núcleo de tritio es mucho menos estable que el núcleo de helio 4, y la diferencia en la energía de unión reduce la energía disponible para la descomposición.

40. Por lo que sabemos, la masa del fotón es cero. Sin embargo, no es posible demostrar mediante experimentos que cualquier cosa es cero; todo lo que podemos hacer es poner un límite superior al número. A partir de 2008, el mejor límite superior experimental sobre la masa del fotón es de aproximadamente\(1\times 10^{-52}\) kg. Supongamos que la masa del fotón realmente no es cero, y que el valor está en la parte superior del rango que es consistente con la evidencia experimental actual. En este caso, lo\(c\) que ocurre en la relatividad ya no se interpretaría como la velocidad de la luz. Al igual que con las partículas materiales, la velocidad\(v\) de un fotón dependería de su energía, y nunca podría ser tan grande como\(c\). Estimar el tamaño relativo\((c-v)/c\) de la discrepancia de velocidad, en el caso de un fotón con una frecuencia de 1 kHz, que se encuentra en el rango de radio de muy baja frecuencia. \ hwans {hwans:foton-masa}

41. El hidrógeno es el único elemento cuyos niveles de energía pueden expresarse exactamente en una ecuación. Calcular la relación\(\lambda_E/\lambda_F\) de las longitudes de onda de las transiciones etiquetadas E y F en el problema 25 en la p. 898. Exprese su respuesta como una fracción exacta, no una aproximación decimal. En un experimento en el que se están midiendo longitudes de onda atómicas, esta relación proporciona una verificación natural y rigurosa de la precisión de los resultados. (consulta de respuesta disponible en lightandmatter.com)

42. Dar una comparación numérica del número de fotones por segundo emitidos por un transmisor de radio FM de cien vatios y una bombilla de cien vatios. (consulta de respuesta disponible en lightandmatter.com)

e/Problema 43.

43. En las pp. 884-885 de la subsección 13.4.4, se utilizó álgebra simple para derivar una expresión aproximada para las energías de los estados en hidrógeno, sin tener que resolver explícitamente la ecuación de Schrödinger. Como entrada al cálculo, se utilizó la proporcionalidad\(U \propto r^{-1}\), que es una característica de la interacción eléctrica. El resultado para la energía del\(n\) th patrón de onda estacionaria fue\(E_n \propto n^{-2}\).

Hay otros sistemas de interés físico en los que tenemos\(U \propto r^k\) para valores de\(k\) además\(-1\). El problema 23 discute el estado fundamental del oscilador armónico, con\(k=2\) (y una constante positiva de proporcionalidad). En la física de partículas, los sistemas llamados charmonium y bottomonium están hechos de pares de partículas subatómicas llamadas quarks, que interactúan según\(k=1\), es decir, una fuerza que es independiente de la distancia. (Aquí tenemos una constante positiva de proporcionalidad, y\(r>0\) por definición. El movimiento resulta no ser demasiado relativista, por lo que la ecuación de Schrödinger es una aproximación razonable). La figura muestra los niveles reales de energía para estos tres sistemas, dibujados con diferentes escalas de energía para que todos puedan mostrarse uno al lado del otro. La secuencia de energías en el hidrógeno se acerca a un límite, que es la energía requerida para ionizar el átomo. En el charmonio, sólo se conocen los tres primeros niveles. ⁸

Generalizar el método utilizado para\(k=-1\) a cualquier valor de\(k\), y encontrar el exponente\(j\) en la proporcionalidad resultante\(E_n \propto n^j\). Comparar el cálculo teórico con el comportamiento de las energías reales mostradas en la figura. Comentar el límite\(k\rightarrow\infty\). (consulta de respuesta disponible en lightandmatter.com)

44. El electrón, protón y neutrón fueron descubiertos, respectivamente, en 1897, 1919 y 1932. El neutrón llegó tarde a la fiesta, y algunos físicos consideraron que era innecesario considerarlo como fundamental. A lo mejor podría explicarse como simplemente un protón con un electrón atrapado en su interior. Las cargas se cancelarían, dando a la partícula compuesta la carga neutra correcta, y las masas al menos aproximadamente tenían sentido (un neutrón es más pesado que un protón). (a) Dado que el diámetro de un protón es del orden de\(10^{-15}\ \text{m}\), utilice el principio de incertidumbre de Heisenberg para estimar el impulso mínimo del electrón atrapado. (consulta de respuesta disponible en lightandmatter.com)
(b) Encuentra la energía cinética mínima del electrón. (answer check available at lightandmatter.com)
(c) Mostrar vía\(E=mc^2\) que la explicación propuesta falla, porque la contribución a la masa del neutrón a partir de la energía cinética del electrón sería muchos órdenes de magnitud demasiado grande.

45. Supongamos que un electrón, en una dimensión, está confinado a una cierta región del espacio de manera que su función de onda viene dada por

\[\begin{equation*} \Psi = \begin{cases} 0 & \text{if } x\lt0 \\ A \sin(2\pi x/L) & \text{if } 0\le x\le L \\ 0 & \text{if } x>L \end{cases} \end{equation*}\]

Determinar la constante\(A\) a partir de la normalización. (consulta de respuesta disponible en lightandmatter.com)

46. En lo siguiente,\(x\) y\(y\) son variables, while\(u\) y\(v\) son constantes. Computar (a)\(\partial(ux\ln (vy))/\partial x\), (b)\(\partial(ux\ln (vy))/\partial y\). (consulta de respuesta disponible en lightandmatter.com)

47. (a) Un radiotransmisor irradia energía\(P\) en todas las direcciones, de manera que la energía se propaga esféricamente. Encuentra la densidad de energía a distancia\(r\). (verificación de respuesta disponible en lightandmatter.com)
(b) Dejar que la longitud de onda sea\(\lambda\). Como se describe en el ejemplo 8 en la p. 842, encuentra el número de fotones en un volumen\(\lambda^3\) a esta distancia\(r\). (verificación de respuesta disponible en lightandmatter.com)
(c) Para una estación transmisora de radio AM de 1000 kHz, asumiendo valores razonables de\(P\) y\(r\), verificar, como se afirma en el ejemplo, que el resultado de la parte b es muy grande.

Contributors and Attributions

Template:ContribCrowell