12.1: La cadena de Markov más simple: el juego de voltear monedas

12.1.1 Descripción del juego

Antes de dar la descripción general de una cadena de Markov, estudiemos algunos ejemplos específicos de cadenas simples de Markov. Uno de los más simples es un juego de “monedero”. Supongamos que tenemos una moneda que puede estar en uno de dos “estados”: cabezas (H) o colas (T). En cada paso, volteamos la moneda, produciendo un nuevo estado que es H o T con igual probabilidad. De esta manera, generamos una secuencia como “HTTHTTHTHH...” Si volvemos a ejecutar el juego, generaríamos otra secuencia diferente, como “HTTTTHHHTTH...” Cada una de estas secuencias es una cadena de Markov.

Este proceso se puede visualizar usando un “diagrama de estados”:

Figura\(\PageIndex{1}\): Diagrama de estado para un juego justo de volteo de monedas.

Aquí, los dos círculos representan los dos estados posibles del sistema, “H” y “T”, en cualquier paso del juego de monedas. Las flechas indican los posibles estados a los que el sistema podría hacer la transición, durante el siguiente paso del juego. Se adjunta a cada flecha un número que da la probabilidad de esa transición. Por ejemplo, si estamos en el estado “H”, hay dos estados posibles a los que podríamos hacer la transición durante el siguiente paso: “T” (con probabilidad\(0.5\)), o “H” (con probabilidad\(0.5\)). Por conservación de la probabilidad, las probabilidades de transición que salgan de cada estado deben sumar hasta una.

A continuación, supongamos que el juego de voltear monedas es injusto. La moneda podría ser más pesada en un lado, por lo que en general es más probable que aterrice en H que en T. También podría ser un poco más probable que aterrice en la misma cara de la que se volteó (las monedas reales en realidad se comportan de esta manera). El diagrama de estado resultante puede verse así:

Figura\(\PageIndex{2}\): Diagrama de estado para un juego (particular) injusto de volteo de monedas.

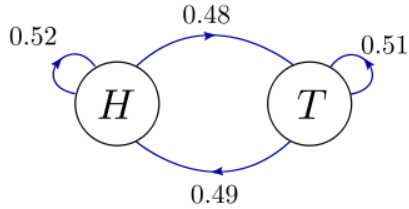
Observe que las probabilidades individuales de transición ya no son\(0.5\), reflejando los efectos injustos antes mencionados. No obstante, las probabilidades de transición que salen de cada estado siguen sumándose a\(1\) (\(0.52+0.48\)saliendo de “H”, y\(0.51+0.49\) saliendo de “T”).

12.1.2 Probabilidades del Estado

Si jugamos el juego injusto anterior muchas veces, H y T tenderán a ocurrir con probabilidades ligeramente diferentes, no exactamente iguales a\(0.5\). En un paso dado, vamos a\(p_{H}\) denotar la probabilidad de estar en el estado H, y\(p_{T}\) la probabilidad de estar en el estado T. Dejar\(P(T|H)\) denotar la probabilidad de transición para pasar de H a T, durante el siguiente paso; y de manera similar para las otras tres transiciones posibles. Según la regla de Bayes, podemos escribir la probabilidad de obtener H en el siguiente paso como

\[p_H' = P(H|H) p_H + P(H|T) p_T.\]

Del mismo modo, la probabilidad de obtener T en el siguiente paso es

\[p_T' = P(T|H) p_H + P(T|T) p_T.\]

Podemos combinarlos en una sola ecuación matricial:

\[\begin{bmatrix}p_H' \\ p_T'\end{bmatrix} = \begin{bmatrix}P(H|H) & P(H|T) \\ P(T|H) & P(T|T)\end{bmatrix} \begin{bmatrix}p_H \\ p_T\end{bmatrix} = \begin{bmatrix}0.52 & 0.49 \\ 0.48 & 0.51\end{bmatrix} \begin{bmatrix}p_H \\ p_T\end{bmatrix}.\]

La matriz de probabilidades de transición se llama matriz de transición. Al inicio del juego, podemos especificar el estado de la moneda para que sea (digamos) H, para que\(p_{H}=1\) y\(p_{T}=0\). Si multiplicamos el vector de probabilidades de estado por la matriz de transición, eso da las probabilidades de estado para el siguiente paso. La multiplicación por los\(K\) tiempos de la matriz de transición da las probabilidades de estado después de\(K\) los pasos.

Después de un gran número de pasos, las probabilidades de los estados podrían converger a una distribución “estacionaria”, de tal manera que ya no cambian significativamente en etapas posteriores. Que estas probabilidades estacionarias sean denotadas por\(\{\pi_H, \pi_T\}\). De acuerdo con la ecuación anterior para las probabilidades de transición, las probabilidades estacionarias deben satisfacer

\[\begin{bmatrix} \pi_H \\ \pi_T \end{bmatrix} = \begin{bmatrix}P(H|H) & P(H|T) \\ P(T|H) & P(T|T)\end{bmatrix} \begin{bmatrix}\pi_H \\ \pi_T\end{bmatrix}.\]

Este sistema de ecuaciones lineales puede resolverse por fuerza bruta (más adelante discutiremos un enfoque más sistemático). El resultado es

\[\pi_H = \frac{P(H|T)}{P(T|H) + P(H|T)}, \quad \pi_T = \frac{P(T|H)}{P(T|H) + P(H|T)} \qquad (\textrm{stationary}\;\textrm{distribution}).\]

Al enchufar los valores numéricos para las probabilidades de transición, terminamos con\(\pi_H = 0.50515, \; \pi_T = 0.49485\).