12.3: El modelo Ehrenfest

12.3.1 Descripción del modelo

El juego de voltear monedas es una cadena de Markov de “dos estados”. Para aplicaciones físicas, a menudo nos interesan las cadenas de Markov donde el número de estados posibles es enorme (por ejemplo, microestados termodinámicos). El modelo Ehrenfest es un ejemplo agradable y sencillo que ilustra muchas de las propiedades de tales cadenas de Markov. Este modelo fue introducido por el equipo físico marido y mujer de Paul y Tatyana Ehrenfest en 1907, con el fin de estudiar la física de la difusión.

Supongamos que tenemos dos cajas, etiquetadas A y B, y un total de partículas\(N\) distinguibles para distribuir entre las dos cajas. En un momento dado, dejar que haya\(n\) partículas en la caja A, y por lo tanto\(N-n\) partículas en la casilla B. Ahora, aplicamos repetidamente el siguiente procedimiento:

1. Escoge aleatoriamente una de las\(N\) partículas (con igual probabilidad).
2. Con probabilidad\(q\), mueva la partícula elegida de cualquier caja que pase a ser a la otra caja. De lo contrario (con probabilidad\(1-q\)), deje la partícula en su caja actual.

Figura\(\PageIndex{1}\): Esquema del modelo Ehrenfest.

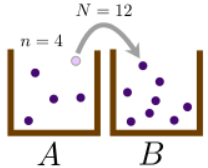
Si hay\(n\) partículas en la caja A, entonces tenemos probabilidad\(n/N\) de elegir una partícula en la casilla A, seguida de una probabilidad de mover esa partícula\(q\) a la caja B. Siguiendo una lógica similar para todas las demás posibilidades, llegamos a tres posibles resultados:

• Mover una partícula de A a B: probabilidad\(nq/N\)
• Mover una partícula de B a A: probabilidad\((N-n)q/N\)
• Dejar el sistema sin cambios: probabilidad\(1-q\)

Se puede comprobar que (i) las probabilidades suman\(1\), y (ii) este resumen es válido para los casos finales\(n=N\) y\(n=0\).

12.3.2 Descripción de la cadena Markov

Podemos etiquetar los estados del sistema usando un entero\(n \in \{0, 1, \dots, N\}\), correspondiente al número de partículas en la casilla A. Hay estados\(N+1\) posibles, y el diagrama de estados es el siguiente:

Figura\(\PageIndex{2}\): Diagrama estatal para el modelo Ehrenfest.

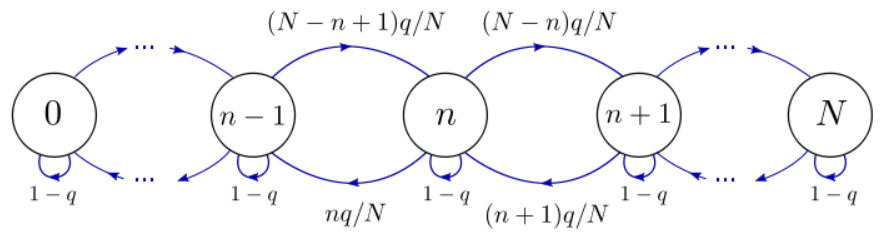
Supongamos que empezamos en estado\(n_{0}=N\), poniendo todas las partículas en la casilla A. A medida que aplicamos repetidamente el procedimiento de Ehrenfest, el sistema pasa por una secuencia de estados,\(\{n_0 = N, n_1, n_2, n_3, \dots\}\), que puede describirse como una cadena de Markov. Trazando el estado\(n_{k}\) versus el número de paso\(k\), vemos una trayectoria aleatoria como la siguiente:

Figura\(\PageIndex{3}\): Trayectoria muestral de un modelo de Ehrenfest con\(N=50\) y\(q=0.5\).

Observe que el sistema se aleja rápidamente de su estado inicial\(n=50\), y se asienta en un comportamiento donde fluctúa alrededor del estado del punto medio\(n=25\). Busquemos la distribución estacionaria, en la que la probabilidad de estar en cada estado no cambia en los pasos posteriores. Dejar\(\pi_{n}\) denotar la probabilidad estacionaria de estar en estado\(n\). Según la regla de Bayes, esta distribución de probabilidad necesita satisfacer

\[\begin{align} \pi_n &= P(n|n-1) \pi_{n-1} + P(n|n) \pi_n + P(n|n+1) \pi_{n+1} \\ & = \frac{N-n+1}{N} \,q\, \pi_{n-1} + (1-q) \pi_n + \frac{n+1}{N}\,q\, \pi_{n+1}. \end{align}\]

Podemos averiguarlo\(\pi_{n}\) usando dos métodos diferentes. El primer método consiste en utilizar nuestros conocimientos de mecánica estadística. En la distribución estacionaria, cada partícula individual debe tener las mismas posibilidades de estar en la casilla A o la caja B. Hay\(2^{N}\) posibles asignaciones de cajas, cada una de las cuales es energéticamente equivalente y por lo tanto tienen iguales probabilidades. De ahí que la probabilidad de encontrar\(n\) partículas en el recuadro A es el número de formas de recoger\(n\) partículas, es decir\(N \choose n\), dividido por el número de posibles asignaciones de cajas. Esto da

\[\pi_n = {N\choose n} \, 2^{-N}.\]

Sustituyendo a la fórmula de la regla de Bayes, podemos verificar que esta distribución es efectivamente estacionaria. Tenga en cuenta que\(\pi_{n}\) resulta ser independiente de\(q\) (la probabilidad de transferir una partícula elegida a la otra caja). Intuitivamente,\(q\) gobierna cuán “rápido” estamos transfiriendo partículas de una caja a otra. Por lo tanto, debería afectar la rapidez con la que el sistema alcanza su comportamiento estacionario o de “equilibrio”, pero no a la distribución estacionaria en sí misma.

12.3.3 Saldo detallado

Hay otra forma de averiguarlo\(\pi_{n}\), que no se basa en adivinar la respuesta de una sola vez. Supongamos que elegimos un par de estados vecinos,\(n\) y\(n+1\), y supongamos que la velocidad a la que se produce la\(n \rightarrow n+1\) transición es la misma que la velocidad a la que ocurre la transición opuesta\(n \rightarrow n+1\),,. No se garantiza que tal condición se mantenga, pero si se mantiene para cada par de estados, entonces la distribución de probabilidad es necesariamente estacionaria. A esta situación se le llama saldo detallado. En cuanto a las probabilidades estatales y probabilidades de transición, el balance detallado requiere

\[P(n+1|n) \, \pi_n = P(n|n+1) \, \pi_{n+1} \qquad \forall n \in \{0,\dots,N\},\]

para esta cadena de Markov. Al conectar las probabilidades de transición, obtenemos la relación de recursión

\[\pi_{n+1} = \frac{N-n}{n+1}\, \pi_{n}.\]

Lo conveniente de esta relación de recursión es que solo involucra\(\pi_{n}\) y\(\pi_{n+1}\), a diferencia de la relación de regla de Bayes que también incluía\(\pi_{n-1}\). Por inducción, ahora podemos demostrar fácilmente que

\[\pi_n = {N\choose n} \pi_0.\]

Por conservación de la probabilidad\(\sum_n \pi_n = 1\),, podemos demostrarlo\(\pi_0 = 2^{-N}\). Esto lleva a

\[\pi_n = {N\choose n} 2^{-N},\]

que es el resultado que antes habíamos adivinado usando argumentos puramente estadísticos.

Para cadenas de Markov más complicadas, puede que no sea posible adivinar la distribución estacionaria; en tales casos, el argumento detallado del equilibrio suele ser el mejor enfoque. Tenga en cuenta, sin embargo, que no se garantiza que se produzca la condición de saldo detallado. Hay algunas cadenas de Markov que no obedecen al balance detallado, por lo que siempre tenemos que verificar que el resultado de la condición de saldo detallado es autoconsistente (es decir, que efectivamente puede ser obedecido por cada par de estados).