3.1: Métrico Minkowski
- Page ID
- 126056
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dos observadores miden la separación temporal y la separación espacial de dos explosiones que ocurren en el espacio interestelar. Un observador encuentra que las explosiones están separadas por\(22\, s\) y\(5.5 \times 10^9\, m\).
- ¿Es posible que el otro observador detecte las dos explosiones como simultáneas? Si es así, ¿a qué distancia están los acontecimientos en este segundo fotograma?
- ¿Es posible que el otro observador detecte que las dos explosiones ocurren en el mismo punto? Si es así, ¿a qué distancia en el tiempo están las dos explosiones en este segundo fotograma?
En el espacio tridimensional clásico, la distancia entre dos eventos puede ser determinada por el Teorema de Pitágoras,
\[(dr)^2 = (dx)^2 + (dy)^2 + (dz)^3 \]
Esta distancia es la misma para dos observadores cualesquiera, incluso si sus mediciones individuales de\(x-\)\(y-\), y\(z\) -separación son diferentes. Esta relación forma un método para calcular la distancia en el espacio tridimensional y se conoce como la métrica del espacio plano tridimensional.
En Relatividad Especial, el Teorema de Pitágoras no es una forma válida de calcular la distancia entre dos eventos. Hermann Minkowski descubrió que si la separación temporal (\(dt\)) y espacial (\(dx\)\(dy\),,\(dz\)) entre dos eventos se combinan de la siguiente manera,
\[ (ds)^2 = (c\,dt )^2 -\left( (dx)^2 + (dy)^2 + (dz)^3 \right) \]
la cantidad resultante, el intervalo espacio-tiempo, es la misma para todos los observadores. Este resultado es la métrica del espacio-tiempo plano de cuatro dimensiones que obedece a la Relatividad Especial. Esta métrica se conoce como la métrica Minkowski.
Dado que esta combinación de separaciones espaciales y temporales es la misma para todos los observadores, podemos usarla para responder a la pregunta anterior. Etiquetar a los dos observadores #1 y #2, y, si los eventos son simultáneos para el observador #2, dt2=0.
Dado que la distancia entre eventos en el fotograma #2 no puede ser la raíz cuadrada de un número negativo, es imposible que ningún otro observador vea estos dos eventos como simultáneos.
Para la parte b, si los dos eventos van a ubicarse en el mismo punto,
Por lo tanto, es posible que otro observador pueda ver que las dos explosiones ocurren exactamente en el mismo punto en el espacio, separadas por 12.2 s de tiempo.
Resolver problemas de relatividad geométricamente
Los aceleradores de partículas aceleran rutinariamente las partículas para acercarse a la velocidad de la luz. Imagínese un electrón viajando a 0.9995c en un acelerador lineal de longitud 3.2 km. ¿Cuánto tiempo tarda el electrón en recorrer la longitud del acelerador, medido por el electrón?
Primero, encuentra el tiempo en el marco del laboratorio usando cinemática básica:
\[t =\dfrac{\Delta x}{v} = \dfrac{3200\,m}{0.9995c} = 1.07 \times 10^{-5} s\]
Este problema ahora podría resolverse fácilmente usando la relación de dilatación del tiempo de relatividad especial. Sin embargo, también se puede resolver mediante un enfoque puramente geométrico utilizando la métrica Minkowski.
Con el observador #1 el laboratorio y #2 el electrón, y los dos eventos el electrón comenzando su viaje y terminando su viaje (que ambos ocurren en el mismo punto en el marco del electrón),
La métrica Minkowski incorpora automáticamente todas las relaciones que discutimos mientras estudiamos la relatividad especial. Esas relaciones son propiedades del espacio-tiempo, no realmente relaciones entre objetos que ocupan el espacio-tiempo, y por lo tanto se construyen en la métrica básica del espacio-tiempo. Esta visión de examinar la métrica del espacio-tiempo para determinar qué sucede con los objetos en el espacio-tiempo forma el marco conceptual de la relatividad general.
Métrico Minkowski en coordenadas polares
Somos libres de expresar la métrica Minkowski en cualquier sistema de coordenadas que sea más útil para el problema que se está investigando. Por ejemplo, la métrica expresada en coordenadas polares es:
\[(ds)^2 = (c\,dt)^2 - (dr)^2 - r^2 (d \phi)^2\]
Observe (en la Figura\(\PageIndex{1}\)) que cada pequeño “paso” en la dirección radial,\(dr\), es exactamente de la misma longitud. La métrica refleja este hecho porque no hay factor multiplicativo frente al\(dr\) término.

Figura\(\PageIndex{1}\): Transformación a coordenadas polares, mostrando vectores de base unitaria. (CC BY-SA; Maksim).
No obstante, la longitud de un “paso” en la dirección tangencial,\(d \phi\), depende de lo lejos que se encuentre del origen. Cuanto más lejos estés del origen, más largo\(d\phi\) es un solo paso adentro. Esto se refleja en el factor multiplicativo de\(r\) '' en la parte tangencial de la métrica. (A medida que r se hace grande, un solo paso se\(d\phi\) hace grande.)
¿Qué significaría si hubiera factores multiplicativos similares frente a las partes temporal y radial de la métrica? Un factor frente a la parte dt de la métrica significaría que los pasos en dt (es decir, clics de un reloj) serían de diferente duración en diferentes lugares. Un factor frente a la parte radial significaría que los escalones radiales eran de diferentes longitudes en diferentes lugares. Sería como tomar la rejilla de coordenadas que se muestra arriba y estirarla en diferentes cantidades en diferentes lugares, dando como resultado un sistema de coordenadas (y espacio subyacente que el sistema de coordenadas está tratando de representar) que ya no es plano, sino más bien deformado o curvo (Figura\(\PageIndex{2}\)).
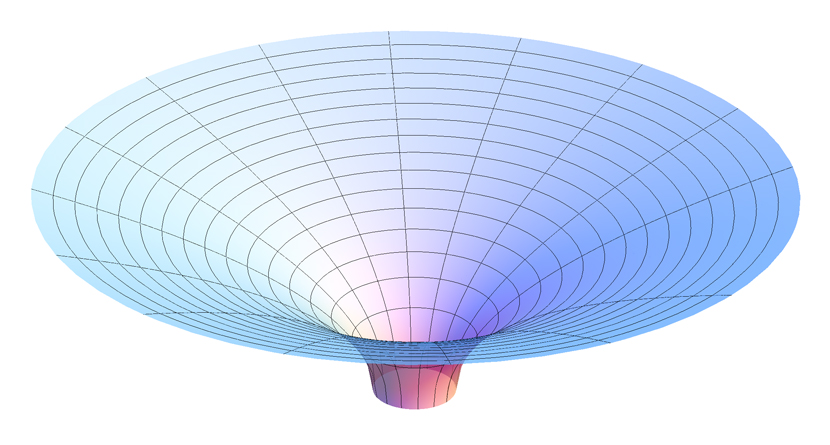
Figura\(\PageIndex{2}\): (CC BY-SA; )
Por ejemplo, si la parte radial de la métrica se multiplicaba por un factor que se volvía grande a medida que\(r\) se volvía pequeño, esto daría como resultado un sistema de coordenadas que se parecía más o menos al de la Figura\(\PageIndex{2}\). Observe que los escalones radiales se hacen cada vez más grandes a medida que la distancia radial se hace cada vez más pequeña. También observe que realmente no hay manera de dibujar adecuadamente este sistema de coordenadas sobre una superficie plana; el sistema de coordenadas es intrínsecamente curvado.


