02. Aplicación de la Relación Impulso-Momentum
- Page ID
- 132893
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aplicación de la Relación Impulso-Momentum
Reexaminemos la misma situación que examinamos al inicio del capítulo anterior, un cohete lanzado directamente hacia arriba con un empuje dependiente del tiempo.
Un cohete de juguete de 2.0 kg está equipado con un motor que proporciona un empuje aproximadamente modelado por la función F (t) = (60 N/s) t - (15 N/s 2) t 2, para 0 < t < 4.0 s, y cero a partir de entonces. El cohete se lanza directamente hacia arriba.
Para el análisis, aplicaremos la relación impulso-impulso entre:
Evento 1: El instante en que el cohete sale de la plataforma de lanzamiento
Evento 2: El instante en que el empuje cae a cero.


Recuerda del último capítulo que el cohete no sale de la plataforma de lanzamiento hasta 0.36 s después de que se encienda el motor.

Cuando el motor se apaga, el cohete viaja a 42.5 m/s hacia arriba.
También podríamos aplicar la relación impulso-impulso entre:
Evento 1: El instante en que el empuje cae a cero.
Evento 2: El instante en que el cohete alcanza su altura máxima.
Durante este intervalo, la única fuerza que actúa sobre el cohete es la fuerza de la gravedad, y la relación impulso-momento es:
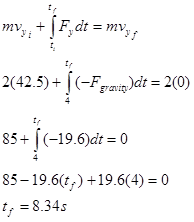
De esta manera, el cohete alcanza su mayor altitud 8.34 s después del lanzamiento.
Es importante señalar que cuando una fuerza es una función del tiempo, es relativamente fácil integrar la función y determinar el impulso. No obstante, debe quedar claro que no sería fácil determinar el trabajo realizado por una fuerza de este tipo. Dado que el trabajo se expresa como una integral de una fuerza con respecto a un desplazamiento (dr), la función de fuerza tiene que expresarse en términos de posición, r. En general, no es una tarea fácil (o a veces posible) “convertir” una función del tiempo en una función de posición, por lo que la energía-trabajo no es particularmente útil manera de analizar sistemas cuando las fuerzas que actúan dependen del tiempo. Sin embargo, si las fuerzas dependen de la posición del objeto, la energía de trabajo es una poderosa herramienta de análisis.
Aplicación de la relación trabajo-energía
Una bola de 0.15 kg se lanza verticalmente hacia arriba por medio de un émbolo accionado por resorte, se tira hacia atrás 8.0 cm y se libera. Se requiere una fuerza de aproximadamente 10 N para empujar el émbolo hacia atrás 8.0 cm.
La fuerza ejercida por un resorte

La fuerza que ejerce el resorte sobre la bola depende de la cantidad en la que se comprima el resorte. Cuanto más se comprime el resorte, mayor es la fuerza que ejerce sobre la pelota. Un modelo común es que la fuerza ejercida por un resorte es directamente proporcional a la cantidad de deformación del resorte, en este caso la compresión. La deformación (es) se define como la diferencia entre la longitud actual del resorte (L) y la longitud de equilibrio (L 0):

Si definimos la dirección de la coordenada positiva para apuntar en la misma dirección que la deformación positiva (estiramiento), entonces
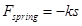
con la constante de proporcionalidad, k, referida como la constante de resorte.
Para el émbolo, ya que se necesitan 10 N para comprimir el resorte 8.0 cm,
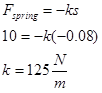
Para el análisis, aplicaremos la relación trabajo-energía entre:
Evento 1: El instante en que se libera el émbolo.
Evento 2: El instante en que la pelota alcanza su altura máxima.
Para estos dos eventos, trabajo-energía se ve así:

Para hacer la integral, debemos expresar F resorte en términos de la variable de integración, r. para el sistema de coordenadas elegido, s y r son idénticos. También tenga en cuenta que la fuerza del resorte y la dirección de movimiento de la bola apuntan en la misma dirección. Así, f = 0.
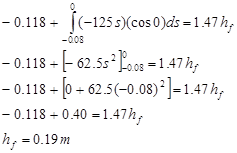
La bola alcanza una altura máxima de 19 cm por encima de la parte superior del émbolo.


