Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

4.2: Dispersión Compton

Última actualización

30 oct 2022
Guardar como PDF
- 4.1: La luz como una corriente de partículas
- 4.3: Producción por pares

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

La dispersión de Compton se refiere a la dispersión de la luz de los electrones libres. Experimentalmente, es imposible crear un objetivo de electrones completamente libres. Sin embargo, si los fotones incidentes tienen una energía mucho mayor que las energías de unión típicas de los electrones a los átomos, los electrones serán “derribados” de los átomos por los fotones y actuarán como partículas libres. Por lo tanto, la dispersión de Compton típicamente se refiere a la dispersión de fotones de alta energía fuera de objetivos atómicos.

Si la luz fuera puramente un fenómeno de onda, una onda entrante con una frecuencia específica haría que el electrón oscilara con la misma frecuencia. El electrón oscilante emitiría entonces ondas electromagnéticas de esta frecuencia. Así, la luz dispersada y la luz entrante tendrían, hasta dentro de una ligera variación debido al efecto Doppler para la luz, la misma frecuencia. Esto no es lo que se ve experimentalmente.

En cambio, imaginemos que la luz es una corriente de fotones y analicemos la colisión de un fotón y un electrón por la conservación de energía y momento. Considera un fotón incidente de longitud de onda $\lambda$ golpeando un electrón estacionario. El fotón se dispersa a ángulo $\theta'$ (y nueva longitud de onda $\lambda'$ ) y el electrón a ángulo $\phi$ .

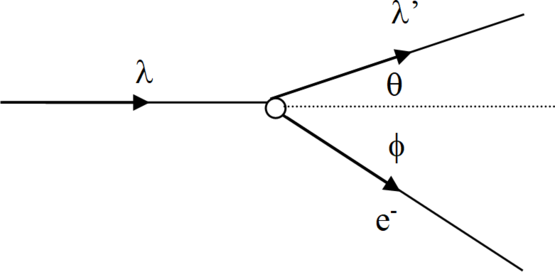
Para analizar, aplicar conservación de energía:

$E + mc^2 = E' + E_e$

$x$ -conservación de impulso:

$pc + 0 = p'c \cos \theta + p_e c \cos \phi$

y $y$ -conservación de impulso:

$0 + 0 = p'c \sin \theta + p_e c \sin \phi$

Para fotones, $E = pc$ , por lo que las ecuaciones de impulso se pueden escribir como:

$p_x: E = E' \cos \theta + p_e \cos \phi$

$p_x: 0 = E' \cos \theta - p_e \sin \phi$

Experimentalmente, es más fácil detectar el fotón disperso que el electrón disperso, por lo que eliminaremos los parámetros del electrón y derivaremos una interrelación entre los diversos parámetros del fotón. Para eliminar $\phi$ , resolver $x$ -momentum y $y$ -momentum para $\cos \phi$ y $\sin \phi$ , y luego cuadrar y sumarlos juntos:

Resolver la ecuación de conservación de energía para $E_e$ :

$E_e = E + mc^2 - E'$

$E_e^2 = ( E + mc^2 -E')^2 \label{eq20}$

Conecte los dos resultados anteriores en la Ecuación\ ref {eq20} para eliminar las variables de electrones:

$E_e^2 = (p_ec)^2 + (mc^2)^2$

$( E + mc^2 -E')^2 = E^2 - 2EE' \cos \theta E'^2 + (mc^2)^2$

Seis términos cancelan y la ecuación simplifica enormemente

$2Emc^2 - 2E'mc^2 - 2EE' = -2EE' \cos \theta$

Reorganizar ng rendimientos

Este resultado relaciona directamente la longitud de onda entrante con la longitud de onda dispersa y el ángulo de dispersión. Todos estos parámetros se miden fácilmente de manera experimental. Por su explicación teórica y verificación experimental de la dispersión de fotones de alta energía, el estadounidense Arthur Compton fue galardonado con el Premio Nobel en 1927.

Uso de la relación de dispersión de Compton

Un fotón de 800 keV choca con un electrón en reposo. Después de la colisión, el fotón se detecta con 650 keV de energía. Encuentra la energía cinética y el ángulo del electrón disperso.

La relación fundamental para la dispersión de Compton es

$\lambda' - \lambda = \dfrac{hc}{mc^2}( 1- \cos \theta)$

donde

$\lambda'$ es la longitud de onda dispersada del fotón,
$\lambda$ es la longitud de onda del fotón incidente,
y $\theta$ es el ángulo del fotón disperso.

Para encontrar la energía cinética del electrón disperso no se requiere usar la fórmula Compton. Si el fotón inicialmente tiene $800\, \text{keV}$ , y después de la dispersión ha $650 \text{keV}$ , entonces $150, \text{keV}$ debe haber sido transferido al electrón. Por lo tanto, $KE_{electron} = 150 \text{keV}$ .

Encontrar el ángulo del electrón disperso implica la relación Compton. Primero, convierte las energías fotónicas en longitudes de onda:

$\begin{align} E_{photon} &= \frac{hc}{\lambda} \\[5pt] \lambda &= \frac{hc}{E} \\[5pt] &= \frac{1240 \text{ eVnm}}{800 \text{ keV}} = 1.55 \times 10^{-3} \text{ nm} \\[5pt] & = \frac{1240 \text{ eVnm}}{650 \text{ keV}} = 1.91 \times 10^{-3} \text{ nm} \end{align}$

luego usa la relación

$\lambda' - \lambda = \frac{hc}{mc^2}(1-\cos\theta)$

$1.91\times 10^{-3} - 1.55 \times 10^{-3} = \lambda = \frac{1240 \text{ eVnm}}{511 \text{ keV}}(1-\cos\theta)$

$0.1484 = (1-\cos\theta)$

$\theta = 31.6°$

Sin embargo, ¡este es el ángulo de dispersión del fotón, no del electrón!

Para encontrar el ángulo de dispersión del electrón, aplique la conservación del momento en la dirección perpendicular a la dirección inicial del fotón.

$0 = p_{\text{scattered photon}}c(\sin\theta)-p_{electron}c(\sin\phi)$

$p_{\text{scattered photon}}c(\sin\theta) =p_{electron}c(\sin\phi)$

$E_{\text{scattered photon}}c(\sin\theta) = \sqrt{E_{electron}^2-(mc^2)^2}(\sin\theta)$

$650\sin(31.6)=\sqrt{(511+150)^2-(511)^2}(\sin\phi)$

$\sin\phi =0.813$

$\phi = 54.4$

Uso de la relación de dispersión de Compton

Support Center

How can we help?