Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

28.3: Trazado

Última actualización

30 oct 2022
Guardar como PDF
- 28.2: Arreglos
- 28.4: El paquete Python de QExpy para física experimental

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

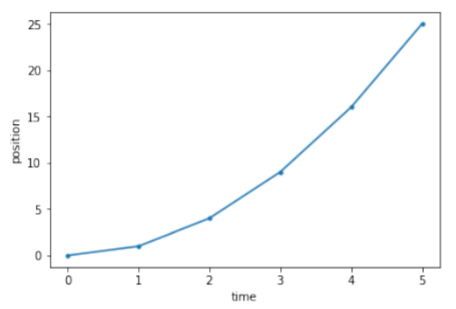
Varios módulos están disponibles en python para el trazado. Aquí mostraremos cómo usar el módulo pylab (que es equivalente al módulo matplotlib). Por ejemplo, podemos trazar fácilmente los datos en las dos matrices de la sección anterior para trazar la posición frente al tiempo para el objeto:

código python $\PageIndex{1}$

Trazado de dos matrices

01#import the pylab module
02import pylab as pl
03 
04#define an array of values for the position of the object
05position = [0 ,1 ,4 ,9 ,16 ,25]
06#define an array of values for the corresponding times
07time = [0 ,1 ,2 ,3 ,4 ,5]
08 
09#make the plot showing points and the line (.−)
10pl.plot(time, position, '.-')
11#add some labels:
12pl.xlabel("time") #label for x-axis
13pl.ylabel("position") #label for y-axis
14#show the plot
15pl.show()

Salida

Figura A4.3.1: Usando dos matrices y trazándolas.

Ejercicio $\PageIndex{1}$

¿Cómo modificarías el código Python anterior para mostrar solo los puntos, y no la línea?

Responder

Podemos usar Python para trazar cualquier función matemática que nos guste. Es importante darse cuenta de que las computadoras no tienen una representación de una función continua. Así, si quisiéramos trazar una función continua, primero necesitamos evaluar esa función en muchos puntos, y luego trazar esos puntos. El módulo numpy proporciona muchas características útiles para trabajar con matrices de números y aplicar funciones directamente a esas matrices.

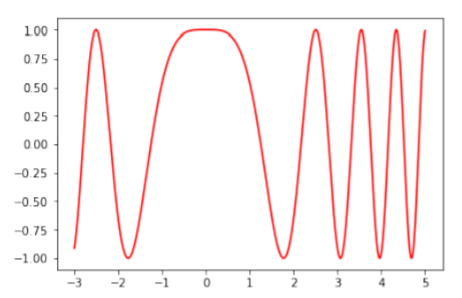
Supongamos que nos gustaría trazar la función $f(x) = cos(x^{2})$ entre $x = −3$ y $x = 5$ . Para hacer esto en Python, primero generaremos una matriz de muchos valores de $x$ entre $−3$ y $5$ usando el paquete numpy y la función linspace (min, max, N) que genera puntos $N$ linealmente espaciados entre min y max . Luego evaluaremos la función en todos esos puntos para crear una segunda matriz. Finalmente, trazaremos las dos matrices una contra la otra:

código python $\PageIndex{2}$

Trazar una función de 1 variable

01#import the pylab and numpy modules
02import pylab as pl
03import numpy as np
04 
05#Use numpy to generate 1000 values of x between -3 and 5.
06#xvals is an array with 1000 values in it:
07xvals = np.linspace(-3,5,1000)
08 
09#Now, evaluate the function for all of those values of x.
10#We use the numpy version of cos, since it allows us to take the cos
11#of all values in the array.
12#fvals will be an array with the 1000 corresponding cosines of the xvals squared
13fvals = np.cos(xvals**2)
14 
15#make the plot showing only a line, and color it
16pl.plot(xvals, fvals, color='red')
17#show the plot
18pl.show()

Salida

Figura A4.3.2: Trazar una función usando matrices.

Support Center

How can we help?