Saltar al contenido principal
LibreTexts Español

15.3: Movimiento periódico

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128134
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Practica la conversión entre frecuencia y periodo

    Periodo y Frecuencia

    La terminología física habitual para el movimiento que se repite una y otra vez es el movimiento periódico, y el tiempo requerido para una repetición se llama el período, a menudo expresado como la letra T. (El símbolo P no se usa debido a la posible confusión con el impulso) Una repetición completa del movimiento se llama ciclo. La frecuencia se define como el número de ciclos por unidad de tiempo. La frecuencia suele ser denotada por una letra latina f o por una letra griega ν (nu). Tenga en cuenta que el periodo y la frecuencia son recíprocos entre sí.

    imagen

    Ondas sinusoidales de frecuencias variables: ondas sinusoidales de diversas frecuencias; las ondas inferiores tienen frecuencias más altas que las anteriores. El eje horizontal representa el tiempo.

    \[\mathrm{f=\dfrac{1}{T}}\]

    Por ejemplo, si el corazón de un bebé recién nacido late a una frecuencia de 120 veces por minuto, su periodo (el intervalo entre latidos) es de medio segundo. Si calibres tu intuición para que esperes que las frecuencias grandes se emparejen con periodos cortos, y viceversa, puedes evitar algunos errores embarazosos en los exámenes de física.

    Unidades

    imagen

    Ruedas de locomotoras: Las ruedas de la locomotora giran a una frecuencia de f ciclos por segundo, lo que también puede describirse como ω radianes por segundo. Los enlaces mecánicos permiten la vibración lineal de los pistones de la máquina de vapor, a la frecuencia f, para accionar las ruedas.

    En unidades SI, la unidad de frecuencia es el hertz (Hz), llamado así por el físico alemán Heinrich Hertz: 1 Hz indica que un evento se repite una vez por segundo. Una unidad de medida tradicional utilizada con dispositivos mecánicos giratorios son las revoluciones por minuto, abreviadas RPM. 60 RPM equivale a un hercio (es decir, una revolución por segundo, o un período de un segundo). La unidad SI por periodo es la segunda.

    Frecuencia Angular

    A menudo, el movimiento periódico se expresa mejor en términos de frecuencia angular, representada por la letra griega ω (omega). La frecuencia angular se refiere al desplazamiento angular por unidad de tiempo (por ejemplo, en rotación) o la velocidad de cambio de la fase de una forma de onda sinusoidal (por ejemplo, en oscilaciones y ondas), o como la velocidad de cambio del argumento de la función sinusoidal.

    \[\mathrm{y(t)= \sin (θ(t))= \sin (ωt)= \sin (2πft)}\]

    \[\mathrm{ω=2πf}\]

    La frecuencia angular a menudo se representa en unidades de radianes por segundo (recuerde que hay 2π radianes en un círculo).

    Periodo de una Misa en un Muelle

    El período de una masa m sobre un resorte de constante de resorte k se puede calcular como\(\mathrm{T=2π \sqrt{\frac{m}{k}}}\).

    objetivos de aprendizaje

    • Identificar los parámetros necesarios para calcular el período y la frecuencia de una masa oscilante en el extremo de un resorte ideal

    Comprender la fuerza restauradora

    La primera ley de Newton implica que un objeto que oscila de un lado a otro está experimentando fuerzas. Sin fuerza, el objeto se movería en línea recta a una velocidad constante en lugar de oscilar. Es importante entender cómo la fuerza sobre el objeto depende de la posición del objeto. Si un objeto está vibrando hacia la derecha y hacia la izquierda, entonces debe tener una fuerza hacia la izquierda sobre él cuando está en el lado derecho, y una fuerza hacia la derecha cuando está en el lado izquierdo. En una dimensión, podemos representar la dirección de la fuerza usando un signo positivo o negativo, y dado que la fuerza cambia de positiva a negativa debe haber un punto en el medio donde la fuerza sea cero. Este es el punto de equilibrio, donde el objeto permanecería en reposo si se liberara en reposo. Es una convención común definir el origen de nuestro sistema de coordenadas para que x sea igual a cero en equilibrio.

    imagen

    Regla Oscilante: Cuando se desplaza de su posición de equilibrio vertical, esta regla de plástico oscila hacia adelante y hacia atrás debido a la fuerza restauradora que se opone al desplazamiento. Cuando el gobernante está a la izquierda, hay una fuerza a la derecha, y viceversa.

    Considera, por ejemplo, desplumar una regla de plástico que se muestra en la primera figura. La deformación de la regla crea una fuerza en la dirección opuesta, conocida como fuerza restauradora. Una vez liberada, la fuerza restauradora hace que la regla retroceda hacia su posición de equilibrio estable, donde la fuerza neta sobre ella es cero. No obstante, para cuando el gobernante llega, gana impulso y continúa moviéndose hacia la derecha, produciendo la deformación opuesta. Luego se fuerza hacia la izquierda, hacia atrás a través del equilibrio, y el proceso se repite hasta que las fuerzas disipativas (por ejemplo, fricción) amortiguan el movimiento. Estas fuerzas eliminan la energía mecánica del sistema, reduciendo gradualmente el movimiento hasta que la regla llega a descansar.

    imagen

    Restauración de fuerza, impulso y equilibrio: (a) La regla plástica ha sido liberada, y la fuerza restauradora está devolviendo la regla a su posición de equilibrio. (b) La fuerza neta es cero en la posición de equilibrio, pero el gobernante tiene impulso y continúa moviéndose hacia la derecha. c) La fuerza restauradora se encuentra en sentido contrario. Detiene al gobernante y lo mueve de nuevo hacia el equilibrio nuevamente. d) Ahora el gobernante tiene ímpetu a la izquierda. e) En ausencia de amortiguación (causada por fuerzas de fricción), la regla alcanza su posición original. A partir de ahí, la moción se repetirá.

    Ley de Hooke

    Las oscilaciones más simples ocurren cuando la fuerza restauradora es directamente proporcional al desplazamiento. El nombre que se le dio a esta relación entre fuerza y desplazamiento es la ley de Hooke:

    \[\mathrm{F=kx}\]

    Aquí, F es la fuerza restauradora, x es el desplazamiento del equilibrio o deformación, y k es una constante relacionada con la dificultad para deformar el sistema (a menudo llamada constante de resorte o constante de fuerza). Recuerde que el signo menos indica que la fuerza restauradora está en la dirección opuesta al desplazamiento. La constante de fuerza k está relacionada con la rigidez (o rigidez) de un sistema: cuanto mayor es la constante de fuerza, mayor es la fuerza restauradora y más rígido es el sistema. Las unidades de k son newtons por metro (N/m). Por ejemplo, k está directamente relacionado con el módulo de Young cuando estiramos una cuerda. Un ejercicio típico de laboratorio de física es medir las fuerzas restauradoras creadas por los resortes, determinar si siguen la ley de Hooke y calcular sus constantes de fuerza si lo hacen.

    Masa en un resorte

    Un ejemplo común de una objeción que oscila de un lado a otro según una fuerza restauradora directamente proporcional al desplazamiento del equilibrio (es decir, siguiendo la Ley de Hooke) es el caso de una masa en el extremo de un resorte ideal, donde “ideal” significa que ninguna variable desordenada del mundo real interfiere con el resultado imaginado.

    El movimiento de una masa sobre un resorte puede describirse como Movimiento Armónico Simple (SHM), el nombre que se le da al movimiento oscilatorio para un sistema donde la fuerza neta puede ser descrita por la ley de Hooke. Ahora podemos determinar cómo calcular el período y la frecuencia de una masa oscilante al final de un resorte ideal. El periodo T puede calcularse conociendo solo la masa, m, y la constante de fuerza, k:

    \[\mathrm{T=2π\sqrt{\frac{m}{k}}}\]

    Al tratar con\(\mathrm{f=\frac{1}{T}}\), la frecuencia viene dada por:

    \[\mathrm{f=\frac{1}{2π} \sqrt{\frac{k}{m}}}\]

    Podemos entender intuitivamente la dependencia de estas ecuaciones de m y k. Si uno aumentara la masa en un sistema de muelles oscilantes con una k dada, la masa incrementada proporcionará más inercia, provocando que disminuya la aceleración debida a la fuerza restauradora F (recuerda la Segunda Ley de Newton:\(\mathrm{F=ma}\)). Esto alargará el periodo de oscilación y disminuirá la frecuencia. En contraste, al aumentar la constante de fuerza k se incrementará la fuerza restauradora según la Ley de Hooke, provocando a su vez que la aceleración en cada punto de desplazamiento también aumente. Esto reduce el periodo y aumenta la frecuencia. El desplazamiento máximo desde el equilibrio se conoce como la amplitud X.

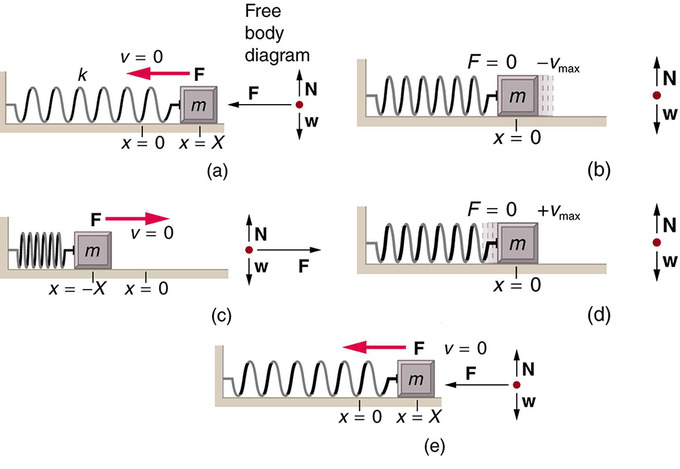
    imagen

    Movimiento de una masa en un resorte ideal: Un objeto unido a un resorte que se desliza sobre una superficie sin fricción es un oscilador armónico simple sin complicaciones. Cuando se desplaza del equilibrio, el objeto realiza un movimiento armónico simple que tiene una amplitud X y un periodo T. La velocidad máxima del objeto se produce a medida que pasa por el equilibrio. Cuanto más rígido es el resorte, menor es el periodo T. Cuanto mayor es la masa del objeto, mayor es el periodo T. (a) La masa ha logrado su mayor desplazamiento X hacia la derecha y ahora la fuerza restauradora hacia la izquierda está en su máxima magnitud. (b) La fuerza restauradora ha movido la masa de nuevo a su punto de equilibrio y ahora es igual a cero, pero la velocidad hacia la izquierda está en su máximo. c) El impulso de la masa la ha llevado a su máximo desplazamiento hacia la derecha. La fuerza restauradora está ahora a la derecha, igual en magnitud y opuesta en dirección en comparación con (a). d) El punto de equilibrio se vuelve a alcanzar, esta vez con ímpetu a la derecha. e) El ciclo se repite.

    Movimiento armónico simple

    El movimiento armónico simple es un tipo de movimiento periódico donde la fuerza restauradora es directamente proporcional al desplazamiento.

    objetivos de aprendizaje

    • Relacionar la fuerza restauradora y el desplazamiento durante el simple movimiento armónico

    Movimiento armónico simple

    El movimiento armónico simple es un tipo de movimiento periódico donde la fuerza restauradora es directamente proporcional al desplazamiento (es decir, sigue la Ley de Hooke). Puede servir como modelo matemático de una variedad de movimientos, como la oscilación de un resorte. Además, otros fenómenos pueden aproximarse por simple movimiento armónico, como el movimiento de un simple péndulo, o vibración molecular.

    Movimiento armónico simple: Una breve introducción al movimiento armónico simple para estudiantes de física basada en cálculo.

    El movimiento armónico simple se caracteriza por el movimiento de una masa sobre un resorte cuando está sujeto a la fuerza restauradora elástica lineal dada por la Ley de Hooke. Un sistema que sigue el movimiento armónico simple se conoce como un simple oscilador armónico.

    Dinámica de la oscilación armónica simple

    Para el movimiento armónico simple unidimensional, la ecuación del movimiento (que es una ecuación diferencial ordinaria lineal de segundo orden con coeficientes constantes) se puede obtener por medio de la segunda ley de Newton y la ley de Hooke.

    \[\mathrm{F_{net}=m\dfrac{d^2x}{dt^2}=−kx,}\]

    donde m es la masa del cuerpo oscilante, x es su desplazamiento desde la posición de equilibrio, y k es la constante elástica. Por lo tanto:

    \[\mathrm{\dfrac{d^2x}{dt^2}=−(\dfrac{k}{m})x.}\]

    Resolviendo la ecuación diferencial anterior, se obtiene una solución que es una función sinusoidal.

    \[\mathrm{x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)=A \cos (ωt−φ),}\]

    donde

    \[\mathrm{ω=\sqrt{\dfrac{k}{m}},}\]

    \[\mathrm{A=\sqrt{c_1^2+c_2^2},}\]

    \[\mathrm{\tan φ=(\dfrac{c_2}{c_1}).}\]

    En la solución, c 1 y c2 son dos constantes determinadas por las condiciones iniciales, y el origen se establece para ser la posición de equilibrio. Cada una de estas constantes lleva un significado físico del movimiento: A es la amplitud (desplazamiento máximo desde la posición de equilibrio),\(\mathrm{ω = 2πf}\) es la frecuencia angular y φ es la fase.

    Podemos usar cálculo diferencial y encontrar la velocidad y aceleración en función del tiempo:

    \[\mathrm{v(t)=\dfrac{dx}{dt}=−Aω \sin (ωt−φ)}\]

    \[\mathrm{a(t)=\dfrac{d^2x}{dt^2}=−Aω^2 \cos (ωt−φ).}\]

    La aceleración también se puede expresar en función del desplazamiento:

    \[\mathrm{a(t)=−ω^2x.}\]

    Entonces desde\(\mathrm{ω = 2πf}\),

    \[\mathrm{f=\dfrac{1}{2π}\sqrt{\dfrac{k}{m}}.}\]

    Recordando que\(\mathrm{T=\frac{1}{f}}\),

    \[\mathrm{T=2π \sqrt{\dfrac{m}{k}}.}\]

    Usando la Segunda Ley de Newton, la Ley de Hooke, y algún Cálculo diferencial, pudimos derivar el periodo y la frecuencia de la masa oscilando en un resorte que encontramos en la última sección. Tenga en cuenta que el periodo y la frecuencia son completamente independientes de la amplitud.

    La siguiente figura muestra el movimiento armónico simple de un objeto sobre un resorte y presenta gráficas de x (t), v (t) y a (t) versus tiempo. Debes aprender a crear conexiones mentales entre las ecuaciones anteriores, las diferentes posiciones del objeto en un resorte en la caricatura, y las posiciones asociadas en las gráficas de x (t), v (t) y a (t).

    imagen

    Visualización de Movimiento Armónico Simple: Gráficas de x (t), v (t) y a (t) versus t para el movimiento de un objeto sobre un resorte. La fuerza neta sobre el objeto puede ser descrita por la ley de Hooke, y así el objeto experimenta un simple movimiento armónico. Tenga en cuenta que la posición inicial tiene el desplazamiento vertical en su valor máximo X; v es inicialmente cero y luego negativo a medida que el objeto se mueve hacia abajo; y la aceleración inicial es negativa, de vuelta hacia la posición de equilibrio y convirtiéndose en cero en ese punto.

    Movimiento armónico simple y movimiento circular uniforme

    El movimiento armónico simple es producido por la proyección de un movimiento circular uniforme sobre uno de los ejes en el plano x-y.

    objetivos de aprendizaje

    • Describir la relación entre el movimiento armónico simple y el movimiento circular uniforme

    Movimiento Circular Uniforme

    El movimiento circular uniforme describe el movimiento de un cuerpo que atraviesa una trayectoria circular a velocidad constante. La distancia del cuerpo desde el centro del círculo permanece constante en todo momento. Aunque la velocidad del cuerpo es constante, su velocidad no es constante: la velocidad (una cantidad vectorial) depende tanto de la velocidad del cuerpo como de su dirección de desplazamiento. Dado que el cuerpo cambia constantemente de dirección a medida que viaja alrededor del círculo, la velocidad también está cambiando. Esta velocidad variable indica la presencia de una aceleración llamada aceleración centrípeta. La aceleración centrípeta es de magnitud constante y está dirigida en todo momento hacia el centro del círculo. Esta aceleración es, a su vez, producida por una fuerza centrípeta, una fuerza de magnitud constante, y dirigida hacia el centro.

    Velocity

    La figura anterior ilustra vectores de velocidad y aceleración para un movimiento uniforme en cuatro puntos diferentes de la órbita. Dado que la velocidad v es tangente a la trayectoria circular, no hay dos velocidades que apunten en la misma dirección. Aunque el objeto tiene una velocidad constante, su dirección siempre está cambiando. Este cambio de velocidad se debe a una aceleración, a, cuya magnitud se mantiene constante (como la de la velocidad), pero cuya dirección también está cambiando siempre. La aceleración apunta radialmente hacia adentro (centrípetamente) y es perpendicular a la velocidad. Esta aceleración se conoce como aceleración centrípeta.

    imagen

    Movimiento Circular Uniforme (en Cuatro Puntos Diferentes en la Órbita): Velocidad v y aceleración a en movimiento circular uniforme a velocidad angular ω; la velocidad es constante, pero la velocidad es siempre tangente a la órbita; la aceleración tiene magnitud constante, pero siempre apunta hacia el centro de rotación

    El desplazamiento alrededor de una trayectoria circular a menudo se da en términos de un ángulo θ. Este ángulo es el ángulo entre una línea recta dibujada desde el centro del círculo hasta la posición inicial de los objetos en el borde y una línea recta dibujada desde la posición final de los objetos en el borde hasta el centro del círculo. Consulte para una representación visual del ángulo donde el punto p comenzó en el eje x y se movió a su posición actual. El ángulo θ describe lo lejos que se movió.

    imagen

    Proyección de Movimiento Circular Uniforme: Un punto P que se mueve en una trayectoria circular con una velocidad angular constante ω está experimentando un movimiento circular uniforme. Su proyección en el eje x experimenta un simple movimiento armónico. También se muestra la velocidad de este punto alrededor del círculo, v−max, y su proyección, que es v. Obsérvese que estas velocidades forman un triángulo similar al triángulo de desplazamiento.

    Para una trayectoria alrededor de un círculo de radio r, cuando se barre un ángulo θ (medido en radianes), la distancia recorrida en el borde del círculo es s = rθ. Puedes probarlo tú mismo recordando que la circunferencia de un círculo es\(\mathrm{2 \pi r}\), así que si el objeto viajó alrededor de todo el círculo (una circunferencia) habrá pasado por un ángulo de\(\mathrm{2 \pi}\) radianes y viajado una distancia de\(\mathrm{2 \pi r}\). Por lo tanto, la velocidad de desplazamiento alrededor de la órbita es:

    \[\mathrm{v=r\dfrac{dθ}{dt}=rω,}\]

    donde la velocidad angular de rotación es ω. (Obsérvese que\(\mathrm{ω = \frac{v}{r}}\).) Así, v es una constante, y el vector de velocidad v también gira con magnitud constante v, a la misma velocidad angular ω.

    Aceleración

    La aceleración en movimiento circular uniforme siempre se dirige hacia adentro y viene dada por:

    \[\mathrm{a=v\dfrac{dθ}{dt}=vω=\dfrac{v^2}{r}.}\]

    Esta aceleración actúa para cambiar la dirección de v, pero no la velocidad.

    Movimiento armónico simple de movimiento circular uniforme

    Hay una manera fácil de producir un movimiento armónico simple mediante el uso de un movimiento circular uniforme. La siguiente figura demuestra una forma de utilizar este método. Una bola está unida a una plataforma giratoria vertical que gira uniformemente, y su sombra se proyecta sobre el piso como se muestra. La sombra experimenta un simple movimiento armónico.

    imagen

    Sombra de una bola que se somete a un movimiento armónico simple: La sombra de una bola que gira a velocidad angular constante ω en un plato giratorio va de un lado a otro en un movimiento armónico simple y preciso.

    La siguiente figura muestra la relación básica entre el movimiento circular uniforme y el movimiento armónico simple. El punto P se desplaza alrededor del círculo a velocidad angular constante ω. El punto P es análogo a la bola sobre una plataforma giratoria en la figura anterior. La proyección de la posición de P sobre un eje fijo experimenta un simple movimiento armónico y es análoga a la sombra del objeto. En un punto en el tiempo asumido en la figura, la proyección tiene la posición x y se mueve hacia la izquierda con velocidad v. La velocidad del punto P alrededor del círculo es igual a |v max |. La proyección de |v max | en el eje x es la velocidad v del movimiento armónico simple a lo largo del eje x.

    Para ver que la proyección experimenta un simple movimiento armónico, tenga en cuenta que su posición x viene dada por:

    \[\mathrm{x=X \cos θ,}\]

    donde θ=ωt, ω es la velocidad angular constante, y X es el radio de la trayectoria circular. Por lo tanto,

    \[\mathrm{x=X \cos ωt.}\]

    La velocidad angular ω está en radianes por unidad de tiempo; en este caso 2π radianes es el tiempo para una revolución T. Es decir,\(\mathrm{ω=\frac{2π}{T}}\). Sustituyendo esta expresión por ω, vemos que la posición x viene dada por:

    \[\mathrm{x(t)= \cos (\dfrac{2πt}{T})=\cos (2πft).}\]

    Nota: Esta ecuación debería resultar familiar a partir de nuestra discusión anterior sobre el movimiento armónico simple.

    El péndulo simple

    Un péndulo simple actúa como un oscilador armónico con un período que depende solo de L y g para amplitudes suficientemente pequeñas.

    objetivos de aprendizaje

    • Identificar parámetros que afectan el periodo de un péndulo simple

    El péndulo simple

    Un péndulo es un peso suspendido de un pivote para que pueda oscilar libremente. Cuando un péndulo es desplazado lateralmente desde su posición de equilibrio de reposo, está sujeto a una fuerza restauradora; una vez que alcanza su punto más alto en su oscilación, la gravedad lo acelerará de nuevo hacia la posición de equilibrio. Cuando se libera, la fuerza restauradora combinada con la masa del péndulo hace que oscile alrededor de la posición de equilibrio, balanceándose hacia adelante y hacia atrás.

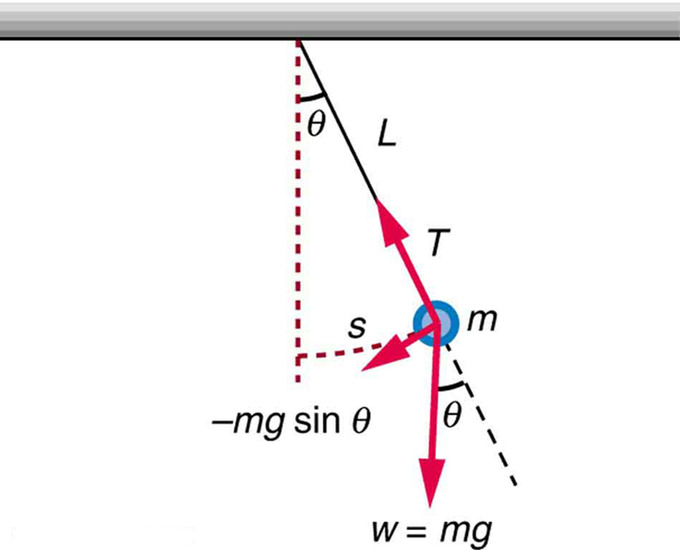
    imagen

    Péndulo simple: Un péndulo simple tiene un bob de diámetro pequeño y una cuerda que tiene una masa muy pequeña pero es lo suficientemente fuerte como para no estirarse apreciablemente. El desplazamiento lineal desde el equilibrio es s, la longitud del arco. También se muestran las fuerzas en el bob, que resultan en una fuerza neta de −mgsinθ hacia la posición de equilibrio, es decir, una fuerza restauradora.

    Para pequeños desplazamientos, un péndulo es un simple oscilador armónico. Un péndulo simple se define para tener un objeto que tiene una masa pequeña, también conocido como el bob de péndulo, el cual está suspendido de un alambre o cuerda de masa despreciable, como se muestra en la figura ilustrativa. Explorando un poco más el péndulo simple, podemos descubrir las condiciones bajo las cuales realiza un movimiento armónico simple, y podemos derivar una expresión interesante para su período.

    Péndulos: Una breve introducción a los péndulos (tanto ideales como físicos) para estudiantes de física basada en cálculo desde el punto de vista del movimiento armónico simple.

    Comenzamos definiendo el desplazamiento para que sea la longitud del arco s. Vemos de la figura que la fuerza neta sobre el bob es tangente al arco y es igual a − mg sin θ. (El peso mg tiene componentes mg cos θ a lo largo de la cuerda y mg sin θ tangente al arco.) La tensión en la cuerda cancela exactamente el componente mg cos θ paralelo a la cuerda. Esto deja una fuerza restauradora neta atrayendo el péndulo hacia la posición de equilibrio en θ = 0.

    Ahora bien, si podemos demostrar que la fuerza restauradora es directamente proporcional al desplazamiento, entonces tenemos un simple oscilador armónico. Al tratar de determinar si tenemos un oscilador armónico simple, debemos señalar que para ángulos pequeños (menores de aproximadamente 15º), sin θ ≈ θ (sin θ y θ difieren en aproximadamente 1% o menos en ángulos más pequeños). Por lo tanto, para ángulos menores de aproximadamente 15º, la fuerza de restauración F es

    \[\mathrm{F≈−mgθ.}\]

    El desplazamiento s es directamente proporcional a θ. Cuando θ se expresa en radianes, la longitud del arco en un círculo se relaciona con su radio (L en este caso) por:

    S=Lθs=Lθ

    para que

    \[\mathrm{θ=sL.}\]

    Para ángulos pequeños, entonces, la expresión para la fuerza restauradora es:

    \[\mathrm{F≈\dfrac{mgL}{s}.}\]

    Esta expresión es de la forma de la Ley de Hooke:

    \[\mathrm{F≈−kx}\]

    donde la constante de fuerza viene dada por k = mg/L y el desplazamiento viene dado por x = s. Para ángulos menores a aproximadamente 15º, la fuerza restauradora es directamente proporcional al desplazamiento, y el péndulo simple es un simple oscilador armónico.

    Usando esta ecuación, podemos encontrar el periodo de un péndulo para amplitudes menores a aproximadamente 15º. Para el péndulo simple:

    \[\mathrm{T=2π\sqrt{\dfrac{m}{k}}=2π\sqrt{\dfrac{m}{\dfrac{mg}{L}}}.}\]

    Por lo tanto,

    \[\mathrm{T=2π\sqrt{\dfrac{L}{g}}}\]

    o el periodo de un simple péndulo. Este resultado es interesante por su sencillez. Las únicas cosas que afectan el periodo de un simple péndulo son su longitud y la aceleración por gravedad. El periodo es completamente independiente de otros factores, como la masa. Incluso los relojes de péndulo simples se pueden ajustar finamente y ser precisos. Obsérvese la dependencia de T sobre g. Si se conoce con precisión la longitud de un péndulo, en realidad se puede utilizar para medir la aceleración debida a la gravedad. Si θ es menor que aproximadamente 15º, el periodo T para un péndulo es casi independiente de la amplitud, como ocurre con los osciladores armónicos simples. En este caso, el movimiento de un péndulo en función del tiempo puede modelarse como:

    \[\mathrm{θ(t)=θ_o \cos (\dfrac{2πt}{T})}\]

    Para amplitudes mayores a 15º, el periodo aumenta gradualmente con amplitud por lo que es más largo que lo dado por la ecuación simple para T anterior. Por ejemplo, a una amplitud de θ 0 = 23° es 1% más grande. El periodo aumenta asintóticamente (hasta el infinito) a medida que θ 0 se acerca a 180°, debido a que el valor θ 0 = 180° es un punto de equilibrio inestable para el péndulo.

    El péndulo físico

    El período de un péndulo físico depende de su momento de inercia alrededor de su punto de pivote y la distancia desde su centro de masa.

    objetivos de aprendizaje

    • Identificar parámetros que afectan el periodo de un péndulo físico

    El péndulo físico

    Recordemos que un péndulo simple consiste en una masa suspendida de una cuerda o varilla sin masa sobre un pivote sin fricción. En ese caso, somos capaces de descuidar cualquier efecto de la propia cuerda o varilla. Por el contrario, un péndulo físico (a veces llamado péndulo compuesto) puede estar suspendido por una varilla que no es sin masa o, más generalmente, puede ser un cuerpo rígido de forma arbitraria que se balancea por un pivote (ver). En este caso, el periodo del péndulo depende de su momento de inercia alrededor del punto de pivote.

    Péndulos — Péndulo Físico: Una breve introducción a los péndulos (tanto ideales como físicos) para estudiantes de física basada en cálculos desde el punto de vista del movimiento armónico simple.

    imagen

    Un péndulo físico: Un ejemplo que muestra cómo actúan las fuerzas a través del centro de masa. Podemos calcular el periodo de este péndulo determinando el momento de inercia del objeto alrededor del punto de pivote.

    La gravedad actúa a través del centro de masa del cuerpo rígido. De ahí que la longitud del péndulo utilizado en las ecuaciones sea igual a la distancia lineal entre el pivote y el centro de masa (h).

    La ecuación de par da:

    \[\mathrm{τ=Iα,}\]

    donde α es la aceleración angular, τ es el par, y I es el momento de inercia.

    El par se genera por gravedad así:

    \[\mathrm{τ=mgh \sin θ,}\]

    donde h es la distancia desde el centro de masa hasta el punto de pivote y θ es el ángulo desde la vertical.

    Por lo tanto, bajo la aproximación de ángulo pequeño sin\ theta\ approx\ theta,

    \[\mathrm{α≈−\dfrac{mghθ}{I}.}\]

    Esto es de la misma forma que el péndulo simple convencional y esto da un periodo de:

    \[\mathrm{T=2π\sqrt{\dfrac{I}{mgh}}.}\]

    Y una frecuencia de:

    \[\mathrm{f=\dfrac{1]{T}=\dfrac{1}{2π}\sqrt{\dfrac{mgh}{I}}.}\]

    En caso de que conozcamos el momento de inercia del cuerpo rígido, podemos evaluar la expresión anterior del periodo para el péndulo físico. Para ilustración, consideremos una varilla rígida uniforme, pivotada desde un marco como se muestra (ver). Claramente, el centro de masa está a una distancia L/2 del punto de suspensión:

    imagen

    Varilla Rígida Uniforme: Una varilla rígida con distribución uniforme de masa cuelga de un punto de pivote. Este es otro ejemplo de péndulo físico.

    \[\mathrm{h=\dfrac{L}{2}.}\]

    El momento de inercia de la varilla rígida alrededor de su centro es:

    \[\mathrm{I_c=\dfrac{mL^2}{12}.}\]

    Sin embargo, necesitamos evaluar el momento de inercia sobre el punto de pivote, no el centro de masa, por lo que aplicamos el teorema del eje paralelo:

    \[\mathrm{I_o=I_c+mh^2=\dfrac{mL^2}{12}+m(\dfrac{L}{2})^2=\dfrac{mL^2}{3}.}\]

    Al conectar este resultado a la ecuación para el período, tenemos:

    \[\mathrm{T=2π\sqrt{\dfrac{I}{mgh}}=2π\sqrt{\dfrac{2mL^2}{3mgL}}=2π\sqrt{\dfrac{2L}{3g}}.}\]

    Lo importante a destacar de esta relación es que el periodo sigue siendo independiente de la masa del cuerpo rígido. Sin embargo, no es independiente de la distribución de masa del cuerpo rígido. Un cambio en la forma, el tamaño o la distribución de la masa cambiará el momento de inercia. Esto, a su vez, cambiará el periodo.

    Al igual que con un péndulo simple, se puede utilizar un péndulo físico para medir g.

    Energía en un oscilador armónico simple

    La energía total en un simple oscilador armónico es la suma constante de las energías potenciales y cinéticas.

    objetivos de aprendizaje

    • Explicar por qué la energía total del oscilador armónico es constante

    Energía en un oscilador armónico simple

    Para estudiar la energía de un simple oscilador armónico, primero consideramos todas las formas de energía que puede tener. Recordemos que la energía potencial (PE), almacenada en una primavera que sigue a la Ley de Hooke es:

    \[\mathrm{PE=\dfrac{1}{2}kx^2,}\]

    donde PE es la energía potencial, k es la constante elástica y x es la magnitud del desplazamiento o deformación. Debido a que un simple oscilador armónico no tiene fuerzas disipativas, la otra forma importante de energía es la energía cinética (KE). La conservación de la energía para estas dos formas es:

    \[\mathrm{KE+PE=constant,}\]

    que se puede escribir como:

    \[\mathrm{\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=constant.}\]

    Esta declaración de conservación de energía es válida para todos los osciladores armónicos simples, incluidos aquellos en los que la fuerza gravitacional juega un papel importante. Por ejemplo, para un péndulo simple reemplazamos la velocidad por v = Lω, la constante de resorte con k = mg/L, y el término de desplazamiento con x = Lθ. Así:

    \[\mathrm{\dfrac{1}{2}mL^2ω^2+\dfrac{1}{2}mgLθ^2=constant.}\]

    En el caso del movimiento armónico simple y sin amortiguar, la energía oscila de un lado a otro entre cinética y potencial, yendo completamente de uno a otro a medida que el sistema oscila. Entonces, para el ejemplo simple de un objeto sobre una superficie sin fricción unida a un resorte, como se muestra nuevamente (ver), el movimiento comienza con toda la energía almacenada en el resorte. A medida que el objeto comienza a moverse, la energía potencial elástica se convierte en energía cinética, convirtiéndose en energía completamente cinética en la posición de equilibrio. Luego es convertida de nuevo en energía potencial elástica por el resorte, la velocidad se vuelve cero cuando la energía cinética se convierte completamente, y así sucesivamente. Este concepto proporciona una visión adicional aquí y en aplicaciones posteriores del movimiento armónico simple, como los circuitos de corriente alterna.

    imagen

    Energía en un oscilador armónico simple: La transformación de la energía en movimiento armónico simple se ilustra para un objeto unido a un resorte en una superficie sin fricción. a) La masa ha logrado el máximo desplazamiento desde el equilibrio. Toda la energía es energía potencial. (b) A medida que la masa pasa por el punto de equilibrio con velocidad máxima, toda la energía en el sistema se encuentra en energía cinética. (c) Una vez más, toda la energía está en la forma potencial, almacenada en la compresión del resorte (en el primer panel la energía se almacenó en la extensión del resorte). (d) Pasando nuevamente por el equilibrio toda la energía es cinética. e) La masa ha completado un ciclo completo.

    El principio de conservación de energía se puede utilizar para derivar una expresión de velocidad v. Si iniciamos nuestro movimiento armónico simple con velocidad cero y desplazamiento máximo (x =X), entonces la energía total es:

    \[\mathrm{E=\dfrac{1}{2}kX^2.}\]

    Esta energía total es constante y se desplaza de un lado a otro entre la energía cinética y la energía potencial, siendo compartida en la mayoría de las veces por cada una. La conservación de energía para este sistema en forma de ecuación es así:

    \[\mathrm{\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=\dfrac{1}{2}kX^2.}\]

    Resolviendo esta ecuación para v rendimientos:

    \[\mathrm{v=±\sqrt{\dfrac{k}{m}(X^2−x^2).}}\]

    La manipulación de esta expresión algebraicamente da:

    \[\mathrm{v=±\sqrt{\dfrac{k}{m}}X\sqrt{1−\dfrac{x^2}{X^2}},}\]

    y así:

    \[\mathrm{v=±v_{max}\sqrt{1−\dfrac{x^2}{X^2}},}\]

    donde:

    \[\mathrm{v_{max}=\sqrt{\dfrac{k}{m}}X.}\]

    A partir de esta expresión, vemos que la velocidad es máxima (v max) a x =0. Observe que la velocidad máxima depende de tres factores. Es directamente proporcional a la amplitud. Como se puede adivinar, cuanto mayor sea el desplazamiento máximo, mayor será la velocidad máxima. También es mayor para sistemas más rígidos porque ejercen mayor fuerza para el mismo desplazamiento. Esta observación se ve en la expresión para v max; es proporcional a la raíz cuadrada de la constante de fuerza k. Finalmente, la velocidad máxima es menor para los objetos que tienen masas mayores, debido a que la velocidad máxima es inversamente proporcional a la raíz cuadrada de m. Para una fuerza dada, los objetos que tienen grandes masas aceleran más lentamente.

    Un cálculo similar para el péndulo simple produce un resultado similar, a saber:

    \[\mathrm{ω_{max}=\sqrt{\dfrac{g}{L}}θ_{max}.}\]

    Experiencia con un simple oscilador armónico: Una masa conocida se cuelga de un resorte de constante elástica conocida y se le permite oscilar. Se mide el tiempo para una oscilación (periodo). Este valor se compara con un valor predicho, basado en la constante de masa y resorte.

    Naturaleza sinusoidal del movimiento armónico simple

    Las soluciones a las ecuaciones de movimiento de los osciladores armónicos simples son siempre sinusoidales, es decir, senos y cosenos.

    objetivos de aprendizaje

    • Revisar los factores responsables del comportamiento sinusoidal del movimiento circular uniforme

    Naturaleza sinusoidal del movimiento armónico simple

    ¿Por qué son tan comunes las ondas seno?

    Si se construyera el sistema de masa sobre un resorte discutido en secciones anteriores y su movimiento se midiera con precisión, su gráfica x — t sería una forma de onda sinusoidal casi perfecta, como se muestra en. Se llama “onda sinusoidal” o “sinusoidal” aunque sea un coseno, o un seno o coseno desplazado en alguna cantidad horizontal arbitraria. Puede que no sea sorprendente que sea un meneo de este tipo general, pero ¿por qué es una forma matemáticamente perfecta específica? ¿Por qué no es una forma de diente de sierra, como en (2); o alguna otra forma, como en (3)? Es notable que una gran cantidad de sistemas vibratorios aparentemente no relacionados muestran la misma característica matemática. Un diapasón, un retoño tirado hacia un lado y liberado, un automóvil rebotando sobre sus amortiguadores, todos estos sistemas exhibirán movimiento de onda sinusoidal bajo una condición: la amplitud del movimiento debe ser pequeña.

    imagen

    Vibraciones sinusoidales y no sinusoidales: Solo el gráfico superior es sinusoidal. Los otros varían con amplitud y período constantes, pero no describen el movimiento armónico simple.

    Ley de Hooke y generación de onda sinusoidal

    La clave para entender cómo vibra un objeto es saber cómo la fuerza sobre el objeto depende de la posición del objeto. Si un sistema sigue la Ley de Hooke, la fuerza restauradora es proporcional al desplazamiento. Como se mencionó en secciones anteriores, existe una ecuación diferencial de segundo orden que relaciona la aceleración y el desplazamiento.

    \[\mathrm{F_{net}=m\dfrac{d^2x}{dt^2}=−kx.}\]

    Cuando se resuelve esta ecuación general para la posición, velocidad y aceleración en función del tiempo:

    • \(\mathrm{x(t)=A \cos (ωt−φ)}\)
    • \(\mathrm{v(t)=\frac{dx}{dt}=−Aω \sin (ωt−φ)}\)
    • \(\mathrm{a(t)=\frac{d^2x}{dt^2}=−Aω^2 \cos (ωt−φ)}\)

    Todas estas son soluciones sinusoidales. Considera una masa en un resorte que tiene un pequeño bolígrafo en su interior que recorre una tira de papel en movimiento a medida que rebota, registrando sus movimientos.

    imagen

    Masa en onda sinusoidal productora de resorte: La posición vertical de un objeto que rebota sobre un resorte se registra en una tira de papel en movimiento, dejando una onda sinusoidal.

    Las ecuaciones anteriores se pueden reescribir en una forma aplicable a las variables para la masa en el sistema de muelles en la figura.

    • \(\mathrm{x(t)=X \cos (\frac{2πt}{T})}\)
    • \(\mathrm{v(t)=−v_{max} \sin (\frac{2πt}{T})}\)
    • \(\mathrm{a(t)=−\frac{kX}{m} \cos (\frac{2πt}{T})}\)

    Recordemos que la proyección de movimiento circular uniforme puede describirse en términos de un simple oscilador armónico. Por lo tanto, el movimiento circular uniforme también es sinusoidal, como se puede ver en.

    imagen

    Naturaleza Sinusoidal del Movimiento Circular Uniforme: La posición de la proyección de movimiento circular uniforme realiza un movimiento armónico simple, como indica esta gráfica ondulada de x versus t.

    Energía instantánea del movimiento armónico simple

    Las ecuaciones discutidas para los componentes de la energía total de los osciladores armónicos simples pueden combinarse con las soluciones sinusoidales para x (t), v (t) y a (t) para modelar los cambios en la energía cinética y potencial en el movimiento armónico simple.

    La energía cinética K del sistema en el tiempo t es:

    \[\mathrm{K(t)=\dfrac{1}{2}mv^2(t)=\dfrac{1}{2}mω^2A^2 \sin ^2 (ωt−φ)=\dfrac{1}{2}kA^2 \sin ^2 (ωt−φ).}\]

    La energía potencial U es:

    \[\mathrm{U(t)=\dfrac{1}{2}kx^2(t)==\dfrac{1}{2}kA^2 \cos ^2(ωt−φ).}\]

    Sumando K (t) y U (t) produce la energía mecánica total vista antes:

    \[\mathrm{E=K+U=\dfrac{1}{2}kA^2.}\]

    Puntos Clave

    • El movimiento que se repite regularmente se llama movimiento periódico. Una repetición completa del movimiento se llama ciclo. La duración de cada ciclo es el periodo.
    • La frecuencia se refiere al número de ciclos completados en un intervalo de tiempo. Es el recíproco del periodo y se puede calcular con la ecuación f=1/t.
    • Algo de movimiento se caracteriza mejor por la frecuencia angular (ω). La frecuencia angular se refiere al desplazamiento angular por unidad de tiempo y se calcula a partir de la frecuencia con la ecuación\(\mathrm{ω=2πf}\).
    • Si un objeto está vibrando hacia la derecha y hacia la izquierda, entonces debe tener una fuerza hacia la izquierda sobre él cuando está en el lado derecho, y una fuerza hacia la derecha cuando está en el lado izquierdo.
    • La fuerza restauradora hace que un objeto oscilante retroceda hacia su posición de equilibrio estable, donde la fuerza neta sobre él es cero.
    • Las oscilaciones más simples ocurren cuando la fuerza restauradora es directamente proporcional al desplazamiento. En este caso la fuerza puede calcularse como\(\mathrm{F=-kx}\), donde F es la fuerza restauradora, k es la constante de fuerza, y x es el desplazamiento.
    • El movimiento de una masa sobre un resorte puede describirse como Movimiento Armónico Simple (SHM): movimiento oscilatorio que sigue la Ley de Hooke.
    • El período de una masa en un resorte viene dado por la ecuación\(\mathrm{T=2π\sqrt{\frac{m}{k}}}\)
    • El movimiento armónico simple a menudo se modela con el ejemplo de una masa en un resorte, donde la fuerza restauradora obedece a la Ley de Hooke y es directamente proporcional al desplazamiento de un objeto desde su posición de equilibrio.
    • Cualquier sistema que obedezca al movimiento armónico simple se conoce como un simple oscilador armónico.
    • La ecuación de movimiento que describe el movimiento armónico simple se puede obtener combinando la Segunda Ley de Newton y la Ley de Hooke en una ecuación diferencial lineal ordinaria de segundo orden:\(\mathrm{F_{net}=m\frac{d^2x}{dt^2}=−kx.}\)
    • El movimiento circular uniforme describe el movimiento de un objeto que recorre una trayectoria circular con velocidad constante. La proyección unidimensional de este movimiento puede describirse como simple movimiento armónico.
    • En movimiento circular uniforme, el vector de velocidad v es siempre tangente a la trayectoria circular y constante en magnitud. La aceleración es constante en magnitud y apunta al centro de la trayectoria circular, perpendicular al vector de velocidad en cada instante.
    • Si un objeto se mueve con velocidad angular ω alrededor de un círculo de radio r centrado en el origen del plano x-y, entonces su movimiento a lo largo de cada coordenada es simple movimiento armónico con amplitud r y frecuencia angular ω.
    • Un simple péndulo se define como un objeto que tiene una masa pequeña, también conocida como el bob de péndulo, que está suspendido de un alambre o cuerda de masa insignificante.
    • Cuando se desplaza, un péndulo oscilará alrededor de su punto de equilibrio debido al impulso en equilibrio con la fuerza restauradora de la gravedad.
    • Cuando los columpios (amplitudes) son pequeños, menores de aproximadamente 15º, el péndulo actúa como un simple oscilador armónico con periodo\(\mathrm{T=2π\sqrt{\frac{L}{g}}}\), donde L es la longitud de la cuerda y g es la aceleración por gravedad.
    • Un péndulo físico es el caso generalizado del péndulo simple. Consiste en cualquier cuerpo rígido que oscile alrededor de un punto de pivote.
    • Para amplitudes pequeñas, el período de un péndulo físico solo depende del momento de inercia del cuerpo alrededor del punto de pivote y la distancia desde el pivote hasta el centro de masa del cuerpo. Se calcula como:\(\mathrm{T=2π\sqrt{\frac{I}{mgh}}}\).
    • El periodo sigue siendo independiente de la masa total del cuerpo rígido. Sin embargo, no es independiente de la distribución de masa del cuerpo rígido. Un cambio en la forma, tamaño o distribución de masa cambiará el momento de inercia y, por lo tanto, el período.
    • La suma de las energías cinéticas y potenciales en un simple oscilador armónico es una constante, es decir,\(\mathrm{KE+PE=constant}\). La energía oscila de un lado a otro entre la cinética y el potencial, yendo completamente de uno a otro a medida que el sistema oscila.
    • En un sistema de muelles, la ecuación de conservación se escribe como:\(\mathrm{\frac{1}{2}mv^2+\frac{1}{2}kx^2=constant=\frac{1}{2}kX^2}\), donde X es el desplazamiento máximo.
    • La velocidad máxima depende de tres factores: amplitud, factor de rigidez, y masa:\(\mathrm{v_{max}=\sqrt{\frac{k}{m}}X}\).
    • Para los osciladores armónicos simples, la ecuación de movimiento es siempre una ecuación diferencial de segundo orden que relaciona la aceleración y el desplazamiento. Las variables relevantes son x, el desplazamiento y k, la constante elástica.
    • Resolver la ecuación diferencial anterior siempre produce soluciones de naturaleza sinusoidal. Por ejemplo,\(\mathrm{x(t), v(t), a(t), K(t),}\) y\(\mathrm{U(t)}\) todos tienen soluciones sinusoidales para el movimiento armónico simple.
    • El movimiento circular uniforme también es sinusoidal porque la proyección de este movimiento se comporta como un simple oscilador armónico.

    Términos Clave

    • periodo: La duración de un ciclo en un evento repetitivo.
    • frecuencia angular: El desplazamiento angular por unidad de tiempo.
    • frecuencia: El cociente del número de veces n un fenómeno periódico se produce a lo largo del tiempo t en que ocurre: f = n/t.
    • Fuerza restauradora: Fuerza variable que da lugar a un equilibrio en un sistema físico. Si el sistema se perturbe lejos del equilibrio, la fuerza restauradora tenderá a llevar al sistema de nuevo hacia el equilibrio. La fuerza restauradora es una función únicamente de la posición de la masa o partícula. Siempre se dirige de nuevo hacia la posición de equilibrio del sistema
    • amplitud: El valor absoluto máximo de alguna cantidad que varía.
    • oscilador armónico simple: Un dispositivo que implementa la ley de Hooke, como una masa que está unida a un resorte, con el otro extremo del resorte conectado a un soporte rígido, como una pared.
    • oscilador: Un patrón que vuelve a su estado original, en la misma orientación y posición, después de un número finito de generaciones.
    • Aceleración centrípeta: Aceleración que hace que un cuerpo siga un camino curvo: siempre es perpendicular a la velocidad de un cuerpo y dirigido hacia el centro de curvatura del camino.
    • Movimiento circular uniforme: Movimiento alrededor de una trayectoria circular con velocidad constante.
    • péndulo simple: Un péndulo hipotético que consiste en un peso suspendido por una cuerda ingrávida.
    • péndulo físico: Un péndulo donde la varilla o cuerda no es sin masa, y puede tener un tamaño extendido; es decir, un cuerpo rígido de forma arbitraria que se balancea por un pivote. En este caso, el periodo del péndulo depende de su momento de inercia alrededor del punto de pivote.
    • distribución de masas: Describe la distribución espacial y define el centro de la masa en un objeto.
    • energía potencial elástica: La energía almacenada en un objeto deformable, como un resorte.
    • fuerzas disipativas: Fuerzas que provocan la pérdida de energía en un sistema en movimiento.
    • sinusoidal: En forma de onda, especialmente aquella cuya amplitud varía en proporción al seno de alguna variable (como el tiempo).

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 15.3: Movimiento periódico is shared under a not declared license and was authored, remixed, and/or curated by Boundless.