Saltar al contenido principal
LibreTexts Español

16.3: Efecto Doppler y Plumas sónicas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128367
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Identificar los parámetros necesarios para calcular la frecuencia percibida por el observador que se mueve hacia la fuente de sonido

    En este átomo, vamos a cubrir el efecto Doppler, pero específicamente cuando el observador es el que está en movimiento.

    El sonido y el efecto Doppler: Este video introduce las ondas sonoras. El primer video describe los fundamentos del sonido mientras que el segundo video mira el Efecto Doppler.

    imagen

    El Efecto Doppler: La misma fuente de sonido está irradiando ondas sonoras a una frecuencia constante en el mismo medio. Sin embargo, ahora la fuente de sonido se mueve hacia la derecha con una velocidad s = 0.7 c (Mach 0.7). Los frentes de onda se producen con la misma frecuencia que antes. Sin embargo, dado que la fuente se está moviendo, el centro de cada nuevo frente de onda ahora está ligeramente desplazado hacia la derecha. Como resultado, los frentes de onda comienzan a amontonarse en el lado derecho (frente a) y se separan más en el lado izquierdo (atrás) de la fuente.

    Cuando el observador se mueve hacia una fuente de sonido, cada onda sucesiva se encuentra antes que la onda anterior. De esta manera, el observador tardará apenas un poco menos de tiempo en escuchar al siguiente. Dado que se reduce el tiempo entre ondas, se incrementa la frecuencia. De manera similar, si el observador se aleja de la fuente de sonido, la frecuencia, y por lo tanto el tono, disminuye. Si bien la frecuencia cambiará si el observador o la fuente de sonido se mueve, es más fácil mostrarla con la fuente de sonido como la que se mueve. Esta figura demostró que la fuente de sonido se mueve:

    A menos que el observador se mueva directamente hacia la fuente de sonido, este ángulo debe tenerse en cuenta al calcular la frecuencia recién percibida. Antes de que podamos iniciar este cálculo, debemos saber:

    • La frecuencia de onda sonora original, f 0
    • La velocidad del observador, v r
    • La velocidad del sonido en el aire, o media, c
    • El ángulo de la línea de visión desde el observador hasta la fuente de sonido, θθ

    Aunque las ondas sonoras se están emitiendo desde la fuente de sonido a una frecuencia uniforme, el observador las percibe de manera diferente. La ecuación para la frecuencia de onda percibida es la siguiente:\(\mathrm{f=\frac{c±v_{r,new}}{c} \times f_0}\) Y la ecuación para v r, es:\(\mathrm{v_{r,new}=v_r \cos θ}\) Si el observador se mueve hacia la fuente de sonido, vas a usar un signo más frente a la velocidad de los observadores. Si el observador se aleja de la fuente de sonido, vas a usar un signo negativo frente a la velocidad de los observadores.

    Fuente móvil

    El efecto Doppler es el cambio aparente en la frecuencia de una onda cuando el observador y la fuente de la onda se mueven uno con relación al otro.

    objetivos de aprendizaje

    • Identificar los parámetros necesarios para calcular la frecuencia percibida de la fuente de sonido que se mueve hacia un observador

    El efecto Doppler: cuando la fuente de sonido está en movimiento

    imagen

    El Efecto Doppler: La misma fuente de sonido está irradiando ondas sonoras a una frecuencia constante en el mismo medio. Sin embargo, ahora la fuente de sonido se mueve hacia la derecha con una velocidad s = 0.7 c (Mach 0.7). Los frentes de onda se producen con la misma frecuencia que antes. Sin embargo, dado que la fuente se está moviendo, el centro de cada nuevo frente de onda ahora está ligeramente desplazado hacia la derecha. Como resultado, los frentes de onda comienzan a amontonarse en el lado derecho (frente a) y se separan más en el lado izquierdo (atrás) de la fuente.

    Cuando la fuente de sonido se mueve hacia un observador, cada onda sucesiva se emite más cerca del observador que la onda anterior y tarda apenas un poco menos de tiempo en llegar al observador que a la anterior. Dado que se reduce el tiempo entre ondas, se incrementa la frecuencia. Del mismo modo, si la fuente de sonido se aleja del observador, la frecuencia (y por lo tanto el tono) disminuye. Si bien la frecuencia cambiará si el observador o la fuente de sonido se mueve, el efecto es demostrado más fácilmente por la fuente de sonido. Este Efecto Doppler se ilustra en.

    A menos que el observador se mueva directamente hacia la fuente de sonido, este ángulo debe ser considerado al calcular la frecuencia recién percibida. Antes de intentar este cálculo, debemos saber:

    • La frecuencia de onda sonora original, f 0
    • La velocidad del observador, v r
    • La velocidad del sonido en el aire, o media, c
    • El ángulo de la línea de visión desde el observador hasta la fuente de sonido,\(\mathrm{θ}\)

    Aunque las ondas sonoras se están emitiendo desde la fuente de sonido a una frecuencia uniforme, el observador las percibe de manera diferente. La ecuación para la frecuencia de onda percibida es la siguiente:\(\mathrm{f=\frac{c}{c±v_{s,new}}∗f_0}\) Y la ecuación para v s, es:
    \[\mathrm{v_{s,new}=v_s \cos θ}\]

    Si la fuente de sonido se mueve hacia el observador, se usa un signo más frente a la velocidad de la fuente de sonido. Si la fuente de sonido se aleja del observador, entonces se usa un signo negativo frente a la velocidad de la fuente de sonido.

    Caso General

    El efecto Doppler es el cambio aparente en la frecuencia de una onda cuando el observador y la fuente de la onda se mueven uno con relación al otro.

    objetivos de aprendizaje

    • Comparar el cambio en la frecuencia debido al efecto Doppler cuando el objeto en movimiento se mueve hacia o lejos del otro objeto

    ¿Alguna vez te has preguntado por qué a medida que un camión de bomberos acelera, el sonido de la sirena parece cambiar? ¿O de dónde viene el sonido muy distinguible en una pista de carreras mientras los autos te baten? Bueno, créanlo o no, ¡esto es ciencia! El nombre de esto se llama el efecto Doppler, llamado así por el científico que lo descubrió. Su nombre era Christian Doppler, y lo descubrió alrededor de 1840 en Praga. Preformó el experimento en dos segmentos. En el primer experimento, hizo que una banda tocara música mientras estaba a bordo de un tren en movimiento, y haría que los observadores escucharan la música en un lugar estacionario mientras pasaba el tren. En el segundo experimento, hizo que un grupo de observadores se sentaran a bordo de un tren en movimiento, mientras la banda tocaba en un lugar estacionario. En ambos casos, los observadores notaron el fenómeno. El cambio en la percepción del sonido puede explicarse a través de la relatividad.

    Cuando la fuente de sonido se mueve hacia un observador, cada onda sucesiva se emite más cerca del observador que la onda anterior. De esta manera, tardará apenas un poco menos de tiempo en llegar al observador que al anterior. Dado que se reduce el tiempo entre ondas, se incrementa la frecuencia. De manera similar, si la fuente de sonido se aleja del observador, la frecuencia, y por lo tanto el tono, disminuye. Si el observador se aleja de la fuente de sonido, la frecuencia se reducirá, y si el observador se acerca a la fuente de sonido, la frecuencia aumenta. Si bien la frecuencia cambiará si el observador o la fuente de sonido se mueve, es más fácil mostrarla con la fuente de sonido como la que se mueve. Esta figura demostró que la fuente de sonido se mueve:

    imagen

    El Efecto Doppler: La misma fuente de sonido está irradiando ondas sonoras a una frecuencia constante en el mismo medio. Sin embargo, ahora la fuente de sonido se mueve hacia la derecha con una velocidad s = 0.7 c (Mach 0.7). Los frentes de onda se producen con la misma frecuencia que antes. Sin embargo, dado que la fuente se está moviendo, el centro de cada nuevo frente de onda ahora está ligeramente desplazado hacia la derecha. Como resultado, los frentes de onda comienzan a amontonarse en el lado derecho (frente a) y se separan más en el lado izquierdo (atrás) de la fuente.

    En la física clásica, donde las velocidades de la fuente y del receptor en relación con el medio son menores que la velocidad de las ondas en el medio, la relación entre la frecuencia observada (f) y la frecuencia emitida (f o) viene dada por:\(\mathrm{f=\frac{(c+vr)}{(c+vs)} \times f_0}\) donde c — velocidad del sonido ondas en el medio, v r — velocidad del observador o receptor, v s — velocidad de la fuente de sonido, y f 0 — frecuencia original de las ondas sonoras.

    La fórmula anterior supone que la fuente se aproxima directamente o retrocediendo del observador. Si la fuente se acerca al observador en ángulo (pero aún con una velocidad constante), la frecuencia observada que se escucha por primera vez es mayor que la frecuencia emitida por el objeto. A partir de entonces, hay una disminución monótona en la frecuencia observada a medida que se acerca al observador, a través de la igualdad cuando está más cerca del observador, y una disminución monotónica continua a medida que retrocede del observador. Cuando el observador está muy cerca de la trayectoria del objeto, la transición de alta a baja frecuencia es muy abrupta. Cuando el observador está lejos de la trayectoria del objeto, la transición de alta a baja frecuencia es gradual.

    Si las velocidades y son pequeñas en comparación con la velocidad de la onda, la relación entre la frecuencia observada y la frecuencia emitida es aproximadamente

    Frecuencia observada:\(\mathrm{f=(1+\frac{Δv}{c})f_0}\)

    Cambio de frecuencia:\(\mathrm{Δf=\frac{Δv}{c}f_0}\)

    donde\(\mathrm{Δv}\) es la velocidad del receptor con respecto a la fuente: es positiva cuando la fuente y el receptor se mueven uno hacia el otro.

    Aumas sónicos

    Un boom sónico es el sonido asociado con las ondas de choque creadas por un objeto que viaja por el aire más rápido que la velocidad del sonido.

    objetivos de aprendizaje

    • Identificar las condiciones que conducen a un boom sónico y discutir sus propiedades

    Aumas sónicos

    Un boom sónico es un sonido asociado con las ondas de choque creadas por un objeto que viaja por el aire más rápido que la velocidad del sonido. Se puede ver como un efecto Doppler sobre los esteroides; los auges sónicos generan una enorme cantidad de energía y suenan como explosiones. El primer objeto hecho por el hombre en crear este fenómeno fue un látigo. El 'crack' del látigo es resultado de este boom sónico. Esta versión de un efecto Doppler es demostrada por.

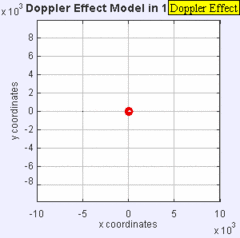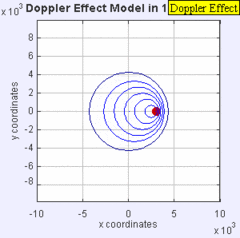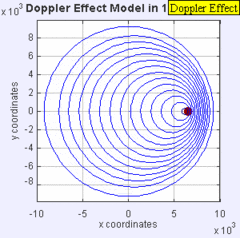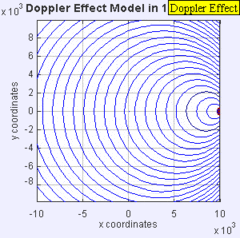
    imagen

    Sonic Boom Gif: La fuente de sonido ahora ha atravesado la barrera de la velocidad del sonido, y está viajando a 1.4 veces la velocidad del sonido, (Mach 1.4). Dado que la fuente se mueve más rápido (con una velocidad) que las ondas sonoras que crea, en realidad lidera el frente de onda que avanza. La fuente de sonido pasará por un observador estacionario (con una velocidad) antes de que el observador realmente escuche el sonido que crea.

    Cuando la fuente de sonido pasa a través del aire, crea una serie de ondas de presión. Estas ondas viajan a la velocidad del sonido, y a medida que aumenta la velocidad de la fuente de sonido, las ondas, al no poder salirse unas de otras, son forzadas juntas. Eventualmente se funden en una sola onda de choque que viaja a la velocidad del sonido. Esta es una velocidad crítica, conocida como Mach. Las ondas de choque irradian desde la fuente de sonido, y crean un “cono Mach”. El medio ángulo, αα, se puede encontrar usando la ecuación

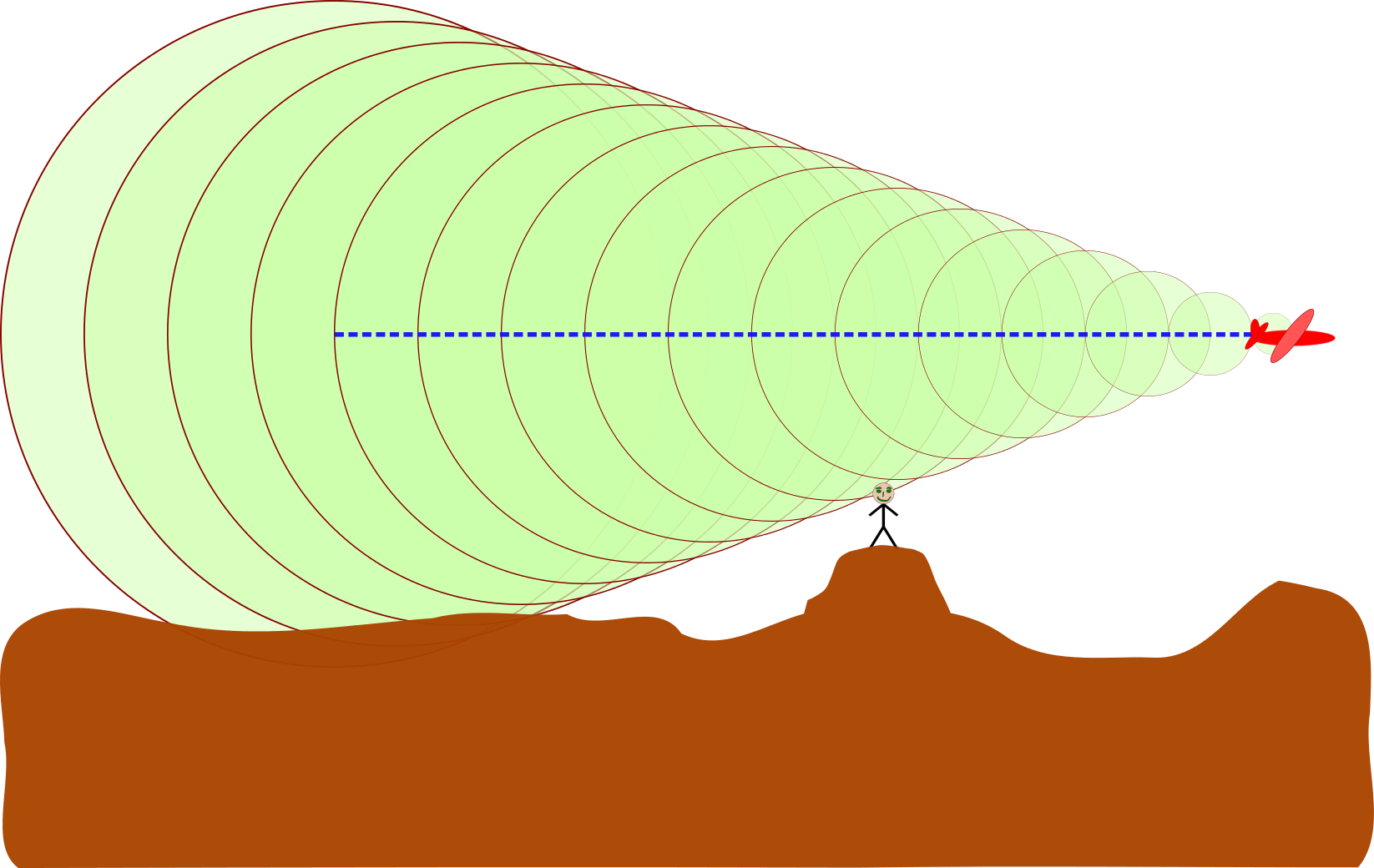
    imagen

    Sonic Boom: Un boom sónico producido por una aeronave que se mueve a M=2.92, calculada a partir del ángulo del cono de 20 grados. Un observador escucha el boom cuando la onda de choque, en los bordes del cono, cruza su ubicación

    \[\mathrm{\sin α= \dfrac{v_s}{v_r}.}\]

    De átomos anteriores, sabemos que\(\mathrm{\frac{v_s}{v_r}}\) es el número de Mach de la fuente de sonido.

    Al frente de la fuente de sonido, hay un aumento repentino de la presión, mientras que al final de la fuente hay una presión decreciente. Este 'perfil de sobrepresión' se conoce como onda N. Hay una gran pluma cuando hay un cambio repentino en la presión, y como la presión cambia dos veces, esta es una pluma doble.

    Puntos Clave

    • Cuando el objeto en movimiento se mueve hacia el otro, la frecuencia se incrementa debido a que se acorta el tiempo entre ondas sonoras sucesivas. Por lo tanto el tono es mayor.
    • Cuando el objeto en movimiento se aleja del otro, la frecuencia disminuye debido a que se alarga el tiempo entre ondas sonoras sucesivas. Por lo tanto, se baja el paso.
    • A menos que los objetos estén en el camino directo del otro, es necesario tener en cuenta el ángulo en el que están uno con relación al otro. La siguiente ecuación necesita ser sustituida por la velocidad de los 'motores'. El ángulo utilizado debe ser el ángulo desde la línea de visión del observador hasta la fuente de sonido. vradial=v*cosθvradial=v*cosθ.
    • Cuando el objeto en movimiento se mueve hacia el otro, la frecuencia se incrementa debido a que se acorta el tiempo entre ondas sonoras sucesivas (por lo tanto el tono es mayor).
    • Cuando el objeto en movimiento se aleja del otro, la frecuencia disminuye debido a que se alarga el tiempo entre ondas sonoras sucesivas (por lo tanto se baja el tono).
    • A menos que los objetos estén en el camino directo del otro, es necesario tener en cuenta su ángulo relativo entre sí. La siguiente ecuación debe ser sustituida por la velocidad de los 'motores'. El ángulo utilizado debe ser el ángulo desde la línea de visión del observador hasta la fuente de sonido.
    • Cuando el objeto en movimiento se mueve hacia el otro, la frecuencia se incrementa debido a que se acorta el tiempo entre ondas sonoras sucesivas. Por lo tanto el tono es mayor.
    • Cuando el objeto en movimiento se aleja del otro, la frecuencia disminuye debido a que se alarga el tiempo entre ondas sonoras sucesivas. Por lo tanto, se baja el paso.
    • Si las velocidades y son pequeñas en comparación con la velocidad de la onda, la relación entre la frecuencia observada y la frecuencia emitida es aproximadamente:\(\mathrm{f=(1+\frac{Δv}{c})f_0}\) dónde\(\mathrm{Δv} \) está la velocidad del receptor con respecto a la fuente: es positiva cuando la fuente y el receptor se mueven uno hacia el otro.
    • Un boom sónico ocurre cuando una fuente de sonido pasa a un observador a una velocidad muy cercana o más rápida que la velocidad del sonido.
    • Los auges sónicos generan una enorme cantidad de energía y suenan como explosiones.
    • El ángulo medio del cono de ondas sonoras producidas por el boom sónico se puede encontrar tomando el seno inverso del número Mach del objeto.

    Términos Clave

    • Efecto Doppler: Cambio aparente en la frecuencia de una onda cuando el observador y la fuente de la onda se mueven uno respecto al otro.
    • física clásica: Todos los aspectos de la física se desarrollaron antes del surgimiento de la mecánica cuántica.
    • frecuencia: El cociente del número de veces n un fenómeno periódico se produce a lo largo del tiempo t en que ocurre:\(\mathrm{f=n/t}\).
    • Número de Mach: La relación entre la velocidad de un cuerpo y la del sonido en el medio circundante.
    • boom sónico: El efecto audible de una onda de choque en el aire, especialmente una causada por un avión que vuela más rápido que la velocidad del sonido

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 16.3: Efecto Doppler y Plumas sónicas is shared under a not declared license and was authored, remixed, and/or curated by Boundless.