Saltar al contenido principal
LibreTexts Español

18.3: Carga puntual

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128011
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Expresar el potencial eléctrico generado por una sola carga puntual en una forma de ecuación

    Potencial eléctrico debido a una carga puntual

    Visión general

    Recordemos que el potencial eléctrico se define como la energía potencial eléctrica por unidad de carga

    \[\mathrm { V } = \frac { \mathrm { PE } } { \mathrm { q } }\]

    El potencial eléctrico te indica cuánta energía potencial tendrá una carga de un solo punto en una ubicación determinada. El potencial eléctrico en un punto es igual a la energía potencial eléctrica (medida en julios) de cualquier partícula cargada en esa ubicación dividida por la carga (medida en culombios) de la partícula. Dado que la carga de la partícula de prueba se ha dividido, el potencial eléctrico es una “propiedad” relacionada únicamente con el campo eléctrico en sí y no con la partícula de prueba. Otra forma de decir esto es que debido a que PE depende de q, el q en la ecuación anterior se cancelará, por lo que V no depende de q.

    La diferencia de potencial entre dos puntos ΔV a menudo se llama voltaje y viene dada por

    \[\mathrm{ΔV=V_B−V_A=\dfrac{ΔPE}{q}}\]

    Cargos puntuales

    Las cargas puntuales, como los electrones, se encuentran entre los bloques de construcción fundamentales de la materia. Además, las distribuciones de carga esféricas (como en una esfera metálica, ver figura abajo) crean campos eléctricos externos exactamente como una carga puntual. El potencial eléctrico debido a una carga puntual es, por lo tanto, un caso que debemos considerar. Usando cálculo para encontrar el trabajo necesario para mover una carga de prueba q desde una gran distancia a una distancia de r de una carga puntual Q, y observando la conexión entre trabajo y potencial (w=—QδV), se puede demostrar que el potencial eléctrico V de una carga puntual es

    \(\mathrm { V } = \frac { \mathrm { k } Q } { \mathrm { r } } \)(carga puntual)

    donde k es una constante igual a 9.0×10 9 Nm 2 /C 2.

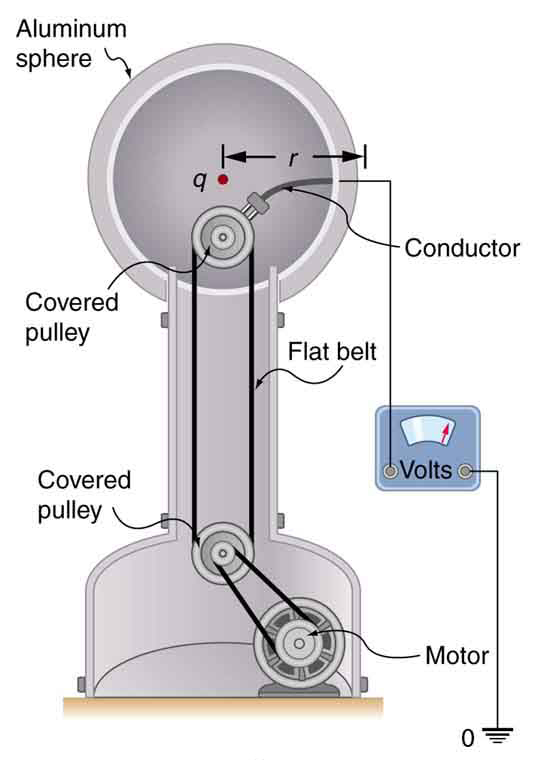
    imagen

    Generador Van de Graaff: El voltaje de esta demostración Generador Van de Graaff se mide entre la esfera cargada y tierra. El potencial de la Tierra se toma como cero como referencia. El potencial de la esfera conductora cargada es el mismo que el de una carga puntual igual en su centro.

    El potencial al infinito se elige para que sea cero. Así, V para una carga puntual disminuye con la distancia, mientras que E para una carga puntual disminuye con la distancia al cuadrado:

    \[\mathrm { E } = \frac { \mathrm { F } } { \mathrm { q } } = \frac { \mathrm { k Q} } { \mathrm { r } ^ { 2 } }\]

    El potencial eléctrico es un escalar mientras que el campo eléctrico es un vector. Observe la simetría entre el potencial eléctrico y el potencial gravitacional, ambos caen en función de la distancia a la primera potencia, mientras que los campos eléctrico y gravitacional caen en función de la distancia a la segunda potencia.

    Superposición de Potencial Eléctrico

    Para encontrar el potencial eléctrico total debido a un sistema de cargas puntuales, se agregan los voltajes individuales como números.

    objetivos de aprendizaje

    • Explicar cómo se encuentra el potencial eléctrico total debido a un sistema de cargas puntuales

    Superposición de Potencial Eléctrico

    Hemos visto que el potencial eléctrico se define como la cantidad de energía potencial por unidad de carga que tiene una partícula de prueba en una ubicación dada en un campo eléctrico, i.e.

    \[\mathrm { V } = \frac { \mathrm { PE } } { \mathrm { q } }\]

    También hemos visto que el potencial eléctrico debido a una carga puntual es

    donde k es una constante igual a 9.0×10 9 Nm 2 /C 2. La ecuación para el potencial eléctrico de una carga puntual es similar a la ecuación para el campo eléctrico generado para una partícula puntual

    \[\mathrm{E=\dfrac{F}{q}=\dfrac{kQ}{r^2}}\]

    con la diferencia de que el campo eléctrico cae con el cuadrado de la distancia mientras que el potencial cae linealmente con la distancia. Esto es análogo a la relación entre el campo gravitacional y el potencial gravitacional.

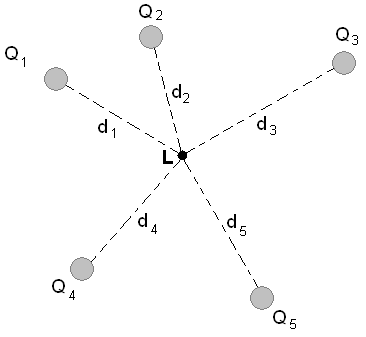
    imagen

    Superposición de Potencial Eléctrico: El potencial eléctrico en el punto L es la suma de voltajes de cada carga puntual (escalares).

    Recordemos que el potencial eléctrico V es un escalar y no tiene dirección, mientras que el campo eléctrico E es un vector. Para encontrar el voltaje debido a una combinación de cargas puntuales, agrega los voltajes individuales como números. Entonces, por ejemplo, en la cifra anterior el potencial eléctrico en el punto L es la suma de las contribuciones potenciales de los cargos Q 1, Q 2, Q 3, Q 4 y Q 5 de manera que

    \[\mathrm { V } _ { \mathrm { L } } = \mathrm { k } \left[ \dfrac { \mathrm{Q}_ { 1 } } { \mathrm { d } _ { 1 } } + \dfrac { \mathrm{Q} _ { 2 } } { \mathrm { d } _ { 2 } } + \dfrac { \mathrm{Q} _ { 3 } } { \mathrm { d } _ { 3 } } + \dfrac { \mathrm{Q} _ { 4 } } { \mathrm { d } _ { 4 } } + \dfrac { \mathrm{Q} _ { 5 } } { \mathrm { d } _ { 5 } } \right]\]

    Para encontrar el campo eléctrico total, se deben agregar los campos individuales como vectores, tomando en cuenta la magnitud y la dirección. Esto es consistente con el hecho de que V está estrechamente asociado con la energía, un escalar, mientras que E está estrechamente asociado con la fuerza, un vector.

    La suma de todas las contribuciones de voltaje para encontrar el campo de potencial total se denomina superposición de potencial eléctrico. Sumar voltajes en lugar de sumar el eléctrico simplifica los cálculos significativamente, ya que la adición de campos escalares potenciales es mucho más fácil que la adición de los campos de vectores eléctricos. Tenga en cuenta que hay casos en los que es posible que necesite sumar contribuciones potenciales de fuentes distintas a los cargos puntuales; sin embargo, eso está más allá del alcance de esta sección.

    Puntos Clave

    • Recordemos que el potencial eléctrico se define como la energía potencial por unidad de carga, i.e\(\mathrm{V=\frac{PE}{q}}\).
    • La diferencia de potencial entre dos puntos ΔV a menudo se llama voltaje y se da b\(\mathrm{ΔV=V_B−V_A=\frac{ΔPE}{q}}\). El potencial a una distancia infinita a menudo se toma como cero.
    • El caso del potencial eléctrico generado por una carga puntual es importante porque es un caso que a menudo se encuentra. Una esfera esférica de carga crea un campo externo al igual que una carga puntual, por ejemplo.
    • La ecuación para el potencial eléctrico debido a una carga puntual es\(\mathrm{V=\frac{kQ}{r}}\), donde k es una constante igual a 9.0×10 9 Nm 2 /C 2.
    • El potencial eléctrico V es un escalar y no tiene dirección, mientras que el campo eléctrico E es un vector.
    • Para encontrar el voltaje debido a una combinación de cargas puntuales, agrega los voltajes individuales como números. Entonces, por ejemplo, en el potencial eléctrico en el punto L está la suma de las contribuciones potenciales de los cargos Q 1, Q 2, Q 3, Q 4, y Q 5 así que eso\(\mathrm { V } _ { \mathrm { L } } = \mathrm { k } \left[ \frac { \mathrm { Q } _ { 1 } } { \mathrm { d } _ { 1 } } + \frac { \mathrm { Q } _ { 2 } } { \mathrm { d } _ { 2 } } + \frac { \mathrm { Q } _ { 3 } } { \mathrm { d } _ { 3 } } + \frac { \mathrm { Q } _ { 4 } } { \mathrm { d } _ { 4 } } + \frac { \mathrm { Q } _ { 5 } } { \mathrm { d } _ { 5 } } \right]\).
    • Para encontrar el campo eléctrico total, se deben agregar los campos individuales como vectores, tomando en cuenta la magnitud y la dirección. Esto es consistente con el hecho de que V está estrechamente asociado con la energía, un escalar, mientras que E está estrechamente asociado con la fuerza, un vector.
    • La suma de todas las contribuciones de voltaje para encontrar el campo de potencial total se denomina superposición de potencial eléctrico. Es mucho más fácil sumar escalares que vectores, por lo que a menudo el método preferido para resolver problemas con campos eléctricos implica la suma de voltajes.

    Términos Clave

    • potencial eléctrico: La energía potencial por unidad de carga en un punto en un campo eléctrico estático; voltaje.
    • voltaje: La cantidad de potencial electrostático entre dos puntos en el espacio.
    • vector: Una cantidad dirigida, una con magnitud y dirección; la entre dos puntos.
    • escalar: Una cantidad que tiene magnitud pero no dirección; comparar vector.
    • superposición: La suma de dos o más contribuciones de campo ocupando el mismo espacio.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 18.3: Carga puntual is shared under a not declared license and was authored, remixed, and/or curated by Boundless.