24.3: Lentes

objetivos de aprendizaje

• Describir las propiedades de una lente delgada y el propósito del trazado de rayos

Lentes Delgadas y Rayos

El trazado de rayos es la técnica de determinar o seguir (trazar) los caminos que toman los rayos de luz. Los experimentos, así como nuestras propias experiencias, muestran que cuando la luz interactúa con objetos varias veces más grandes que su longitud de onda, viaja en líneas rectas y actúa como un rayo. (Un rayo es simplemente una línea recta que se origina en un punto.) Sus características de onda no son pronunciadas en tales situaciones. Dado que la longitud de onda de la luz es inferior a una micra (una milésima de milímetro), actúa como un rayo en las muchas situaciones comunes en las que se encuentra con objetos mayores que una micra, como las lentes.

Para los rayos que pasan por la materia, se utiliza la ley de la refracción para trazar los caminos. Aquí utilizamos el trazado de rayos para ayudarnos a comprender la acción de las lentes en situaciones que van desde la formación de imágenes en película hasta la ampliación de letra pequeña y la corrección de la miopía. Si bien el trazado de rayos para lentes complicados, como los que se encuentran en cámaras sofisticadas, puede requerir técnicas informáticas, existe un conjunto de reglas simples para trazar los rayos a través de lentes delgadas. Una lente delgada se define como aquella cuyo espesor permite que los rayos se refracten, como se ilustra en, pero no permite propiedades como dispersión y aberraciones. Una lente delgada ideal tiene dos superficies refractantes pero la lente es lo suficientemente delgada como para suponer que los rayos de luz se doblan solo una vez. Otra forma de decir esto es que el grosor de la lente es mucho más pequeño que la distancia focal de la lente. Una lente simétrica delgada tiene dos puntos focales, uno a cada lado y ambos a la misma distancia de la lente. (Ver.) Otra característica importante de una lente delgada es que los rayos de luz a través de su centro son desviados en una cantidad insignificante, como se ve en los rayos centrales en las dos primeras figuras. El tratamiento de una lente como una lente delgada se conoce como la “aproximación de lente delgada”.

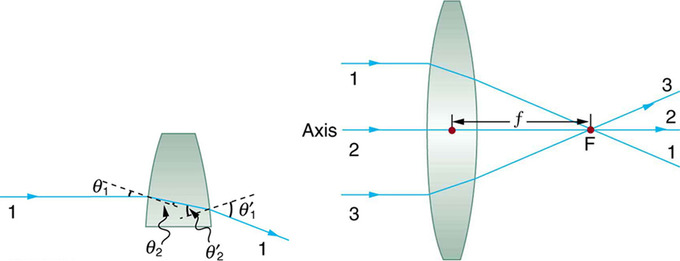
Lente convexa: Los rayos de luz que entran en una lente convergente paralela a su eje convergen en su punto focal F. (El rayo 2 se encuentra en el eje de la lente.) La distancia desde el centro de la lente hasta el punto focal es la distancia focal de la lente f. Una vista ampliada de la trayectoria tomada por el rayo 1 muestra la perpendiculares y los ángulos de incidencia y refracción en ambas superficies.

Lente Delgada: Las lentes delgadas tienen la misma distancia focal en cada lado. a) Rayos de luz paralelos que ingresan a una lente convergente desde la cruz derecha en su punto focal a la izquierda. b) Los rayos de luz paralelos que ingresan a una lente divergente desde la derecha parecen provenir del punto focal de la derecha.

Reglas para el trazado de rayos

Usando papel, lápiz y un borde recto, el trazado de rayos puede describir con precisión el funcionamiento de una lente. Las reglas para el trazado de rayos para lentes delgadas se basan en las ilustraciones incluidas en esta sección:

1. Un rayo que entra en una lente convergente paralela a su eje pasa a través del punto focal F de la lente en el otro lado. (Ver rayos 1 y 3 pulg.)
2. Un rayo que entra en una lente divergente paralela a su eje parece provenir del punto focal F. (Ver rayos 1 y 3 pulg.)
3. Un rayo que pasa por el centro de una lente convergente o divergente no cambia de dirección. (Ver rayo 2 pulgadas y.)
4. Un rayo que entra en una lente convergente a través de su punto focal sale paralelo a su eje. (El reverso de los rayos 1 y 3 pulg.)
5. Un rayo que entra en una lente divergente dirigiéndose hacia el punto focal en el lado opuesto sale paralelo al eje. (El reverso de los rayos 1 y 3 pulgadas).

Lente divergente: Los rayos de luz que entran en una lente divergente paralela a su eje son divergentes, y todos parecen originarse en su punto focal F. Las líneas discontinuas no son rayos, indican las direcciones de las que parecen provenir los rayos. La distancia focal f de una lente divergente es negativa. Una vista ampliada de la trayectoria tomada por el rayo 1 muestra las perpendiculares y los ángulos de incidencia y refracción en ambas superficies.

Diagramas de Rayos, Lente Cóncava y Espejo Convexo: Muestra cómo dibujar los diagramas de rayos para ubicar la imagen producida por una lente cóncava y un espejo convexo.

La ecuación y el aumento de la lente delgada

La ecuación de lente delgada relaciona la distancia d _o del objeto, la distancia d _i de la imagen y la distancia focal f.

objetivos de aprendizaje

• Formular cinco reglas básicas de trazado de rayos

La ecuación y el aumento de la lente delgada

Formación de Imagen por Lentes Delgadas

¿Cómo forma una lente una imagen de un objeto? Podemos utilizar la técnica del trazado de rayos para ilustrar cómo las lentes forman imágenes. También podemos desarrollar ecuaciones para describir las imágenes cuantitativamente. Recordemos las cinco reglas básicas del trazado de rayos:

1. Un rayo que entra en una lente convergente paralela a su eje pasa a través del punto focal F de la lente en el otro lado.
2. Un rayo que entra en una lente divergente paralela a su eje parece provenir del punto focal F.
3. Un rayo que pasa por el centro de una lente convergente o divergente no cambia de dirección.
4. Un rayo que entra en una lente convergente a través de su punto focal sale paralelo a su eje.
5. Un rayo que entra en una lente divergente dirigiéndose hacia el punto focal en el lado opuesto sale paralelo al eje.

Considere un objeto a cierta distancia de una lente convergente, como se muestra en. Para encontrar la ubicación y el tamaño de la imagen formada, trazamos los caminos de los rayos de luz seleccionados que se originan desde un punto en el objeto (en este caso la parte superior de la cabeza de la persona). La figura muestra tres rayos desde la parte superior del objeto que se pueden rastrear usando las cinco reglas de trazado de rayos. Los rayos dejan este punto yendo en muchas direcciones, pero nos concentramos solo en unos pocos con caminos que son fáciles de trazar. El primer rayo es aquel que ingresa a la lente paralelo a su eje y pasa por el punto focal del otro lado (regla 1). El segundo rayo pasa por el centro de la lente sin cambiar de dirección (regla 3). El tercer rayo pasa a través del punto focal más cercano en su camino hacia la lente y deja la lente paralela a su eje (regla 4). Los tres rayos se cruzan en el mismo punto del otro lado de la lente. En este punto se ubica la imagen de la parte superior de la cabeza de la persona. Todos los rayos que provienen de un mismo punto en la parte superior de la cabeza de la persona son refractados de tal manera que crucen en el punto que se muestra. Rayos de otro punto sobre el objeto, como la hebilla de su cinturón, también se cruzarán en otro punto común, formando una imagen completa, como se muestra. Si bien se trazan tres rayos, solo son necesarios dos para localizar la imagen. Lo mejor es trazar rayos para los cuales existen reglas simples de trazado de rayos. Antes de aplicar el trazado de rayos a otras situaciones, consideremos el ejemplo mostrado con más detalle.

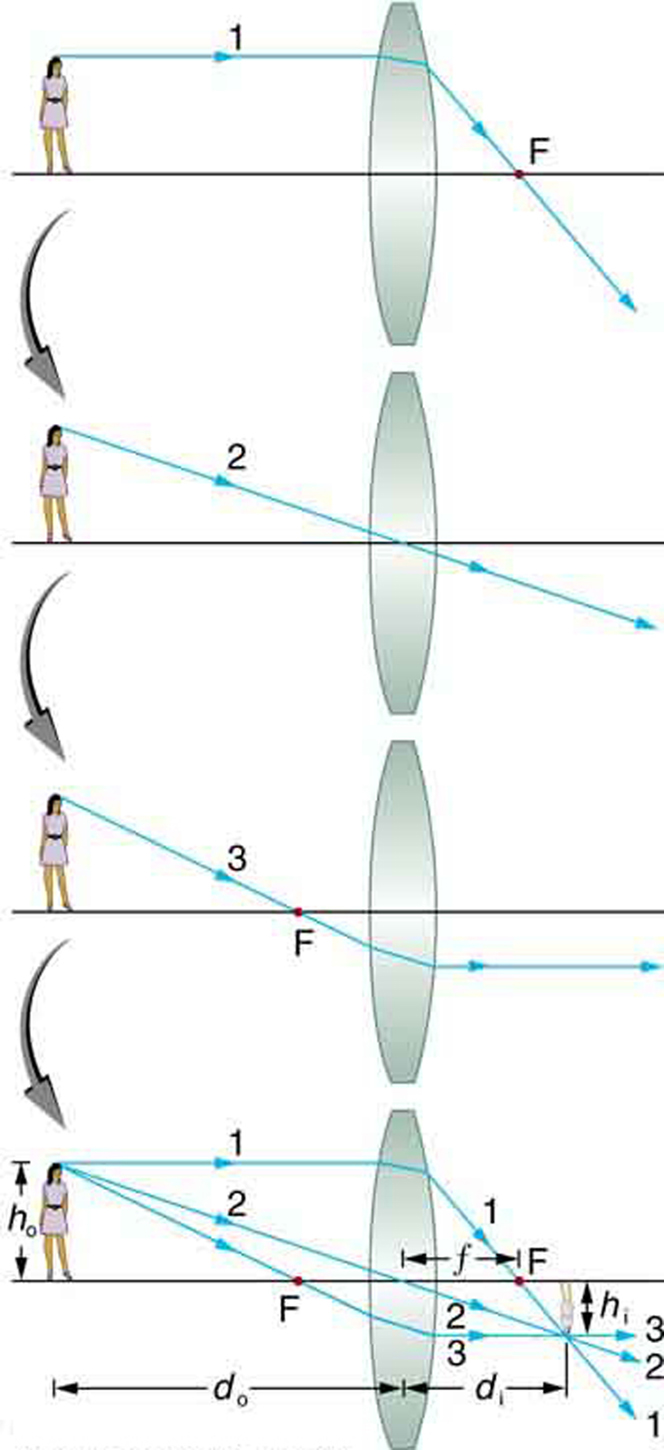
Formación de Imagen con Lente Delgada: El trazado de rayos se utiliza para localizar la imagen formada por una lente. Se trazan los rayos que se originan desde el mismo punto sobre el objeto; los tres rayos elegidos siguen cada uno una de las reglas para el trazado de rayos, de manera que sus caminos son fáciles de determinar. La imagen se ubica en el punto donde se cruzan los rayos. En este caso, se forma una imagen real, una que se puede proyectar en una pantalla.

Varias distancias importantes aparecen en. Definimos d _o como la distancia del objeto, la distancia de un objeto desde el centro de una lente. La distancia d _i de la imagen se define como la distancia de la imagen desde el centro de una lente. A la altura del objeto y la altura de la imagen se les dan los símbolos h _o y h _i, respectivamente. Las imágenes que aparecen verticales con relación al objeto tienen alturas que son positivas y las que están invertidas tienen alturas negativas. Usando las reglas del trazado de rayos y haciendo un dibujo a escala con papel y lápiz, así en, podemos describir con precisión la ubicación y el tamaño de una imagen. Pero el beneficio real del trazado de rayos está en visualizar cómo se forman las imágenes en una variedad de situaciones. Para obtener información numérica, utilizamos un par de ecuaciones que se pueden derivar de un análisis geométrico de trazado de rayos para lentes delgadas. La ecuación de lente delgada es:

\[\dfrac { 1 } { \mathrm { d } _ { o } } + \dfrac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \dfrac { 1 } { \mathrm { f } }\]

Definimos la relación entre la altura de la imagen y la altura del objeto (h _i/h _o) como la ampliación m. El aumento se relaciona con d _o, d _i, h _o y h _i por la siguiente relación:

\[\dfrac { \mathrm { h } _ { \mathrm { i } } } { \mathrm { h } _ { \mathrm { o } } } = - \dfrac { \mathrm { d } _ { \mathrm { i } } } { \mathrm { d } _ { \mathrm { o } } } = \mathrm { m }\]

En muchos casos, ambas ecuaciones se denominan juntas como las ecuaciones de lente delgada s. Las ecuaciones de lentes delgadas son ampliamente aplicables a todas las situaciones que involucran lentes delgadas (y espejos “delgados”).

Ecuaciones de Lente Delgada para una Lente Convexa: Muestra cómo usar la ecuación de lente delgada para calcular la distancia de la imagen, la altura de la imagen y la orientación de la imagen para lentes convexas cuando la distancia del objeto es mayor que la distancia focal (f).

Combinaciones de lentes

Una lente compuesta es una matriz de lentes simples con un eje común.

objetivos de aprendizaje

• Calcular la distancia focal para una lente compuesta a partir de las distancias focales de lentes simples

LENTES COMPUESTAS

A diferencia de una lente simple, que consiste en un solo elemento óptico, una lente compuesta es una matriz de lentes simples (elementos) con un eje común. El uso de múltiples elementos permite la corrección de más aberraciones ópticas, como la aberración cromática causada por el índice de refracción dependiente de la longitud de onda en vidrio, de lo que es posible usando una sola lente. En muchos casos estas aberraciones pueden compensarse en gran medida mediante el uso de una combinación de lentes simples con aberraciones complementarias.

El caso más simple es donde las lentes se colocan en contacto: si las lentes de las distancias focales f ₁ y f ₂ son “delgadas”, la distancia focal combinada f de las lentes viene dada por

\[\dfrac { 1 } { f } = \dfrac { 1 } { f _ { 1 } } + \dfrac { 1 } { f _ { 2 } }\]

Dado que 1/ f es el poder de una lente, se puede ver que los poderes de las lentes delgadas en contacto son aditivos.

Si dos lentes delgadas están separadas en el aire por alguna distancia d (donde d es menor que la distancia focal de la primera lente), la distancia focal para el sistema combinado viene dada por

\[\dfrac { 1 } { f } = \dfrac { 1 } { f _ { 1 } } + \dfrac { 1 } { f _ { 2 } } - \dfrac { d } { f _ { 1 } f _ { 2 } }\]

DISTANCIA FOCAL TRASERA

La distancia desde la segunda lente hasta el punto focal de las lentes combinadas se denomina distancia focal posterior (BFL).

\[\mathrm { BFL } = \dfrac { \mathrm { f } _ { 2 } \left( \mathrm { d } - \mathrm { f } _ { 1 } \right) } { \mathrm { d } - \left( \mathrm { f } _ { 1 } + \mathrm { f } _ { 2 } \right) }\]

Como d tiende a cero, el valor de la BFL tiende al valor de f dado para lentes delgadas en contacto.

Si la distancia de separación es igual a la suma de las distancias focales (d = f ₁ + f ₂), la distancia focal combinada y BFL son infinitas. Esto corresponde a un par de lentes que transforman un haz paralelo (colimado) en otro haz colimado (ver). Este tipo de sistema se denomina sistema afocal, ya que no produce convergencia neta ni divergencia del haz. Dos lentes en esta separación forman el tipo más simple de telescopio óptico. Aunque el sistema no altera la divergencia de una viga colimada, sí altera la anchura de la viga. La ampliación de dicho telescopio viene dada por

Telescopio Kepleriano: Todos los telescopios refractarios utilizan los mismos principios. La combinación de una lente objetivo 1 y algún tipo de ocular 2 se utiliza para reunir más luz de la que el ojo humano podría recoger por sí solo, enfocarla 5 y presentar al espectador una imagen virtual 6 más brillante, más clara y ampliada. El aumento se puede encontrar dividiendo la distancia focal de la lente objetivo por la distancia focal del ocular.

\[\mathrm { M } = - \dfrac { \mathrm { f } _ { 2 } } { \mathrm { f } _ { 1 } }\]

que es la relación entre el ancho del haz de entrada y el ancho del haz de salida. Observe la convención de signos: un telescopio con dos lentes convexas (f ₁ > 0, f ₂ > 0) produce un aumento negativo, lo que indica una imagen invertida. Una lente convexa más una cóncava (f ₁ > 0 > f ₂) produce un aumento positivo y la imagen es vertical.

ACROMATOS

Una lente acromática o acromática es una lente que está diseñada para limitar los efectos de la aberración cromática y esférica. Las lentes acromáticas se corrigen para enfocar dos longitudes de onda (típicamente rojo y azul/violeta) en el mismo plano.

El tipo más común de acromático es el doblete acromático, el cual se compone de dos lentes individuales hechas de vidrios con diferentes cantidades de dispersión Típicamente, un elemento es un elemento negativo (cóncavo) hecho de pedernal, que tiene una dispersión relativamente alta, y el otro es un elemento positivo (convexo) hecho de vidrio corona, que tiene menor dispersión. Los elementos de lente están montados uno al lado del otro, a menudo cementados entre sí, y conformados de manera que la aberración cromática de uno se contrapone con la del otro.

En el tipo más común (mostrado en), la potencia positiva del elemento de lente de corona no es igualada por la potencia negativa del elemento de lente de pedernal. Juntos forman una lente positiva débil que traerá dos longitudes de onda diferentes de luz a un foco común. También se hacen dobletes negativos, en los que predomina el elemento negativo-poder.

Doblete acromático: a) La aberración cromática es causada por la dependencia del índice de refracción de una lente en el color (longitud de onda). La lente es más potente para violeta (V) que para rojo (R), produciendo imágenes con diferentes ubicaciones y aumentos. (b) Los sistemas de lentes múltiples, como este doblete acromático, pueden corregir parcialmente las aberraciones cromáticas, pero pueden requerir lentes de diferentes materiales y sumar al gasto de sistemas ópticos como las cámaras.

La ecuación del fabricante de lentes

La fórmula del fabricante de lentes se utiliza para relacionar los radios de curvatura, el grosor, el índice de refracción y la distancia focal de una lente gruesa.

objetivos de aprendizaje

• Compara lentes finas idealizadas con lentes reales

La ecuación del fabricante de lentes

Lentes Gruesas

A diferencia de las lentes delgadas idealizadas, las lentes reales tienen un grosor finito entre sus dos superficies de curvatura. Una lente delgada ideal con dos superficies de igual curvatura tendría cero potencia óptica, lo que significa que no convergería ni divergiría la luz. Una lente cuyo grosor no es despreciable se llama lente gruesa. En este caso, no podemos simplemente suponer que un rayo de luz sólo se refracta una vez mientras viaja a través de la lente. En cambio, la extensión de la refracción debe depender del grosor de la lente.

Las lentes se clasifican por la curvatura de las dos superficies ópticas. Una lente es biconvexa (o doble convexa, o simplemente convexa) si ambas superficies son convexas. Si la lente es biconvexa, un haz de luz que viaja paralelo al eje de la lente y que pasa a través de la lente será convergido (o enfocado) a un punto en el eje, a cierta distancia detrás de la lente (es decir, la distancia focal). En este caso, la lente se denomina lente positiva o convergente. Consulte para ver un diagrama de una lente positiva (convergente).

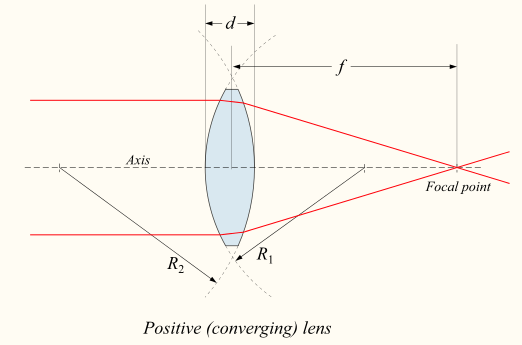
Lente Convergente Gruesa: Diagrama de una lente positiva (convergente). La fórmula del fabricante de lentes relaciona los radios de curvatura, el índice de refracción de la lente, el grosor de la lente y la distancia focal.

Si la lente es bicóncava, un haz de luz que pasa a través de la lente es divergido (extendido); la lente se denomina así lente negativa o divergente. El haz después de pasar a través de la lente parece estar emanando de un punto particular en el eje frente a la lente; la distancia desde este punto a la lente también se conoce como la distancia focal, aunque es negativa con respecto a la distancia focal de una lente convergente. Consulte para ver un diagrama de una lente negativa (divergente).

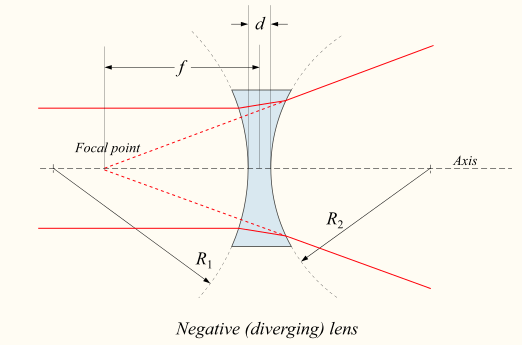
Lente divergente negativa: Diagrama de una lente negativa (divergente). La fórmula del fabricante de lentes relaciona los radios de curvatura, el índice de refracción de la lente, el grosor de la lente y la distancia focal.

La distancia focal de una lente gruesa en el aire se puede calcular a partir de la ecuación del fabricante de lentes:

\[\mathrm { P } = \dfrac { 1 } { \mathrm { f } } = ( \mathrm { n } - 1 ) \left[ \dfrac { 1 } { \mathrm { R } _ { 1 } } - \dfrac { 1 } { \mathrm { R } _ { 2 } } + \dfrac { ( \mathrm { n } - 1 ) \mathrm { d } } { \mathrm { nR } _ { 1 } \mathrm { R } _ { 2 } } \right]\]

donde

• P es la potencia de la lente,
• f es la distancia focal de la lente,
• n es el índice de refracción del material de la lente,
• _R1 es el radio de curvatura de la superficie de la lente más cercana a la fuente de luz,
• _R2 es el radio de curvatura de la superficie de la lente más alejada de la fuente de luz, d y es el grosor de la lente (la distancia a lo largo del eje de la lente entre los dos vértices de la superficie).

Firma convención de Radios R ₁ y R ₂

Los signos de los radios de curvatura de la lente indican si las superficies correspondientes son convexas o cóncavas. La convención de signos utilizada para representar esto varía, pero para nuestro tratamiento si _R1 es positivo la primera superficie es convexa, y si _R1 es negativa la superficie es cóncava. Los signos se invierten para la superficie posterior de la lente: si _R2 es positivo la superficie es cóncava, y si _R2 es negativa la superficie es convexa. Si cualquiera de los radios es infinito, la superficie correspondiente es plana. Con esta convención los signos están determinados por las formas de las superficies de la lente, y son independientes de la dirección en la que la luz viaja a través de la lente.

Aproximación de lente delgada

La ecuación anterior puede simplificarse en gran medida si el grosor d de la lente es muy pequeño en comparación con _R1 y _R2. En este caso, entonces se puede hacer la aproximación de lente delgada y la ecuación del fabricante de lentes se puede aproximar como

\[\mathrm { P } = \dfrac { 1 } { \mathrm { f } } \approx ( \mathrm { n } - 1 ) \left[ \dfrac { 1 } { \mathrm { R } _ { 1 } } - \frac { 1 } { \mathrm { R } _ { 2 } } \right]\]

La distancia focal f es positiva para lentes convergentes y negativa para lentes divergentes. El recíproco de la distancia focal, 1/ f, es la óptica de la lente. Si la distancia focal es en metros, esto da la potencia óptica en dioptrías (metros inversos).

Las lentes tienen la misma distancia focal cuando la luz viaja de atrás hacia adelante que cuando la luz va de adelante hacia atrás, aunque otras propiedades de la lente, como las aberraciones, no son necesariamente las mismas en ambas direcciones.

Refracción a través de lentes

Debido a que el índice de refracción de una lente es mayor que el aire, un rayo se mueve hacia la perpendicular a medida que entra y se aleja a medida que sale.

objetivos de aprendizaje

• Comparar el efecto de una lente convexa y una lente cóncava sobre los rayos de luz

Refracción a través de lentes

Las lentes se encuentran en una enorme variedad de instrumentos ópticos, que van desde la simple lupa hasta una lente de cámara y la lente del ojo humano. La palabra lente deriva de la palabra latina para frijol de lenteja, cuya forma es similar a la de la lente convexa (como se muestra en). La lente convexa está conformada de manera que todos los rayos de luz que entran en ella paralelos a su eje se cruzan entre sí en un solo punto en el lado opuesto de la lente. El eje se define como una línea normal a la lente en su centro (como se muestra en). Tal lente se llama lente convergente (o convexa) por el efecto correspondiente que tiene sobre los rayos de luz. La vista expandida de la trayectoria de un rayo a través de la lente ilustra cómo el rayo cambia de dirección tanto a medida que entra como a medida que sale de la lente.

Dado que el índice de refracción de la lente es mayor que el del aire, el rayo se mueve hacia la perpendicular a medida que entra, y alejándose de la perpendicular a medida que sale (esto es conforme a la ley de refracción). Debido a la forma de la lente, la luz se dobla hacia el eje en ambas superficies. El punto en el que se cruzan los rayos se define como el punto focal F de la lente. La distancia desde el centro de la lente hasta su punto focal se define como la distancia focal f de la lente. muestra cómo una lente convergente, como la de una lupa, puede concentrar (converger) los rayos de luz casi paralelos del sol hacia un pequeño punto.

Lupa: La luz solar enfocada por una lupa convergente puede quemar papel. Los rayos de luz del sol son casi paralelos y cruzan en el punto focal de la lente. Cuanto más potente sea la lente, más cerca de la lente cruzarán los rayos.

Cuanto mayor efecto tenga una lente sobre los rayos de luz, más potente se dice que es. Por ejemplo, una potente lente convergente enfocará los rayos de luz paralelos más cerca de sí mismo y tendrá una distancia focal más pequeña que una lente débil. La luz también se enfocará en un punto más pequeño, más intenso para una lente más potente. La potencia P de una lente se define como la inversa de su distancia focal. En forma de ecuación:

\[\mathrm { P } = \dfrac { 1 } { \mathrm { f } }\]

muestra el efecto de una lente cóncava sobre los rayos de luz que entran en ella paralela a su eje (la trayectoria tomada por el rayo 2 en la figura es el eje de la lente). La lente cóncava es una lente divergente, ya que hace que los rayos de luz se doblen (diverjan) de su eje. En este caso, la lente está conformada de manera que todos los rayos de luz que entran en ella paralelos a su eje parecen originarse desde el mismo punto F, definido como el punto focal de una lente divergente. La distancia desde el centro de la lente hasta el punto focal se llama de nuevo la distancia focal f de la lente. Tenga en cuenta que la distancia focal y la potencia de una lente divergente se definen como negativas. Por ejemplo, si la distancia a F in es de 5.00 cm, entonces la distancia focal es f=—5.00 cm y la potencia de la lente es P=—20 D. La vista expandida de la trayectoria de un rayo a través de la lente ilustra cómo la forma de la lente (dada la ley de refracción) hace que el rayo siga su trayectoria particular y sea divergido.

En secciones posteriores examinaremos la técnica de trazado de rayos para describir la formación de imágenes por lentes. Adicionalmente, exploraremos cómo se pueden cuantificar las ubicaciones y características de las imágenes con la ayuda de un conjunto de ecuaciones de óptica geométrica.

Puntos Clave

• Cuando la luz interactúa con objetos varias veces más grandes que su longitud de onda, viaja en líneas rectas y actúa como un rayo. Un rayo es simplemente una línea recta que se origina en un punto.
• El trazado de rayos es el método para determinar los caminos que la luz toma a través de la materia, como los sistemas ópticos que incluyen lentes.
• Una lente delgada se define como aquella con un grosor que permite que los rayos se refracten, como se ilustra en, pero que no permite propiedades como dispersión y aberraciones. Una lente delgada ideal tiene dos superficies refractantes pero la lente es lo suficientemente delgada como para asumir que los rayos de luz se doblan solo una vez.
• Existen cinco reglas básicas para trazar los rayos a través de una lente.
• El trazado de rayos se puede utilizar para construir una imagen a partir de los rayos de luz que se originan en un objeto que pasa a través de una lente. La imagen se ubica en el punto donde se cruzan los rayos. Al elegir varios puntos de un objeto se puede construir toda la imagen.
• Definimos do para ser la distancia del objeto, la distancia de un objeto desde el centro de una lente. La distancia de imagen di se define como la distancia de la imagen desde el centro de una lente. A la altura del objeto y la altura de la imagen se les dan los símbolos ho y hi, respectivamente.
• La ecuación de lente delgada proporciona rápidamente la relación entre d _i, d _o y la distancia focal f. Se puede derivar de un análisis geométrico de trazado de rayos para lentes delgadas y viene dada por\(\frac { 1 } { \mathrm { d } _ { \mathrm { o } } } + \frac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \frac { 1 } { \mathrm { f } }\).
• El aumento m de una imagen es la relación entre la imagen y la altura del objeto (h _i/h _o). El aumento se relaciona con d _o, d _i, h _o, y h _i por la siguiente relación:\(\frac { \mathrm { h } _ { \mathrm { i } } } { \mathrm { h } _ { \mathrm { o } } } = - \frac { \mathrm { d } _ { \mathrm { i } } } { \mathrm { d } _ { \mathrm { o } } } = \mathrm { m }\).
• El uso de múltiples elementos permite la corrección de más aberraciones ópticas, como la abberación cromática causada por el índice de refracción dependiente de la longitud de onda en vidrio, de lo que es posible usando una sola lente.
• Si las lentes de las distancias focales f ₁ y f ₂ son “delgadas”, la distancia focal combinada f de las lentes viene dada por\(\frac { 1 } { f } = \frac { 1 } { f _ { 1 } } + \frac { 1 } { f _ { 2 } }\) mientras que si las lentes están separadas por alguna distancia d entonces la distancia focal combinada viene dada por\(\frac { 1 } { f } = \frac { 1 } { f _ { 1 } } + \frac { 1 } { f _ { 2 } } - \frac { d } { f _ { 1 } f _ { 2 } }\).
• Si la distancia de separación es igual a la suma de las distancias focales (d = f ₁ + f ₂), la distancia focal combinada es infinita. Esto corresponde a un par de lentes que transforman un haz colimado en otro haz colimado. Este tipo de sistema se llama sistema afocal (un simple telescopio óptico).
• Un doblete acromático es un tipo de lente compuesta diseñada para enfocar dos longitudes de onda (típicamente rojo y azul/violeta) en el mismo plano. Esto corrige (parcialmente) la aberración cromática que se encuentra en una sola lente simple. Ver.
• Si una lente es biconvexa, un haz de luz que viaja paralelo al eje de la lente y que pasa a través de la lente se enfocará a un punto en el eje, a cierta distancia detrás de la lente (es decir, la distancia focal). En este caso, la lente se denomina lente positiva o convergente. Ver.
• Si una lente es bicóncava, un haz de luz que pasa a través de la lente es divergido (extendido); la lente se denomina así lente negativa o divergente. Ver.
• La distancia focal de una lente gruesa en el aire se puede calcular a partir de la ecuación del fabricante de lentes:\(\mathrm { P } = \frac { 1 } { \mathrm { f } } = ( \mathrm { n } - 1 ) \left[ \frac { 1 } { \mathrm { R } _ { 1 } } - \frac { 1 } { \mathrm { R } _ { 2 } } + \frac { ( \mathrm { n } - 1 ) \mathrm { d } } { \mathrm { nR } _ { 1 } \mathrm { R } _ { 2 } } \right]\).
• Los signos de los radios de curvatura de la lente indican si las superficies correspondientes son convexas o cóncavas. Los signos se invierten para la superficie posterior de la lente: si _R2 es positivo la superficie es cóncava, y si _R2 es negativa la superficie es convexa.
• La ecuación del fabricante de lentes puede simplificarse en gran medida si el grosor d de la lente es muy pequeño en comparación con _R1 y _R2. En este caso, entonces se puede hacer la aproximación de lente delgada y la ecuación del fabricante de lentes se puede aproximar como\(P = \frac { 1 } { f } \approx ( n - 1 ) \left[ \frac { 1 } { R _ { 1 } } - \frac { 1 } { R _ { 2 } } \right]\).
• Recordemos que el rayo a se doblará a medida que ingresa a un medio con un índice de refracción diferente. Dado que el índice de refracción de una lente es mayor que el aire, un rayo de luz se moverá hacia la perpendicular a medida que entra y se aleja a medida que sale.
• Se ha conformado una lente convexa de manera que todos los rayos de luz que entran en ella paralelos a su eje se cruzan entre sí en un solo punto en el lado opuesto de la lente (el punto focal). Tal lente se llama lente convergente (o convexa) por el efecto convergente que tiene sobre los rayos de luz. Ver.
• Una lente cóncava es una lente divergente, ya que provoca que los rayos de luz se doblen (diverjan) de su eje. muestra el efecto que tiene sobre los rayos de luz que entran en él paralelos a su eje (la trayectoria tomada por el rayo 2 en la figura es el eje de la lente).
• Cuanto mayor efecto tenga una lente sobre los rayos de luz, más potente se dice que es. Una potente lente convergente enfocará los rayos de luz paralelos más cerca de sí mismo y tendrá una distancia focal más pequeña que una lente débil. La potencia de una lente viene dada por la ecuación\(\mathrm { P } = \frac { 1 } { \mathrm { f } }\).

Términos Clave

• punto focal: Un foco, un punto en el que convergen los rayos de luz u otra radiación.
• trazado de rayos: Una técnica utilizada en óptica para el análisis de sistemas ópticos.
• lente delgada: Una lente delgada se define como aquella cuyo grosor permite que los rayos se refracten pero no permita propiedades como dispersión y aberraciones.
• ecuación de lente fina: relaciona la distancia del objeto do, la distancia de la imagen di y la distancia focal f:\( \frac { 1 } { \mathrm { d } _ { \mathrm { o } } } + \frac { 1 } { \mathrm { d } _ { \mathrm { i } } } = \frac { 1 } { \mathrm { f } }\)
• distancia de imagen: La distancia de la imagen desde el centro de la lente.
• magnificación: La aparente ampliación de un objeto en una imagen.
• aberración: La convergencia a diferentes focos, por una lente o espejo, de los rayos de luz que emanan de un mismo punto, o la desviación de dichos rayos de un solo foco; defecto en un mecanismo de enfoque que impide el punto focal pretendido.
• Sistema afocal: Un sistema óptico que no produce convergencia neta o divergencia del haz, es decir, tiene una distancia focal efectiva infinita. Este tipo de sistema se puede crear con un par de elementos ópticos donde la distancia entre los elementos es igual a la suma de la distancia focal de cada elemento (d = f1+f2).
• Doblete acromático: Un tipo de lente compuesto por dos lentes simples emparejados entre sí diseñados para que la aberración cromática de cada lente desplace parcialmente a la otra; de esta manera la luz en un rango de longitudes de onda puede llevarse al mismo foco.
• lente gruesa: Lentes cuyos grosores no son despreciables (es decir, no se puede hacer la simple suposición de que un rayo de luz se refracta solo una vez en la lente).
• vértices superficiales: Los puntos donde cada superficie cruza el eje óptico. Son importantes principalmente porque son los parámetros físicamente medibles para la posición de los elementos ópticos, por lo que las posiciones de los otros puntos cardinales deben conocerse con respecto a los vértices para describir el sistema físico.
• lente convexa: Una lente que tiene al menos una superficie convexa, de manera que la luz que pasa a través de ella, puede enfocarse.
• lente cóncava: Lente que tiene al menos una superficie cóncava, de manera que los rayos de luz que pasan a través de ella se doblan alejándose de su eje óptico

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• Colegio OpenStax, Colegio de Física. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42452/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/. Licencia: CC BY: Atribución
• Rory Adams, Proyecto gratuito de textos de ciencias de secundaria, Mark Horner, y Heather Williams, Óptica Geométrica - Grado 10. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m32826/latest/. Licencia: CC BY: Atribución
• Lente simple. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Simple_lens. Licencia: CC BY-SA: Atribución-CompartirIgual
• Lente (óptica). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lens_ (óptica). Licencia: CC BY-SA: Atribución-CompartirIgual
• Trazado de rayos (física). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Ray_Tracing_ (física). Licencia: CC BY-SA: Atribución-CompartirIgual
• Aproximación de lente fina. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Thin_Lens_Aproximación. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicada en: www.boundless.com//physics/'thin-lens. Licencia: CC BY-SA: Atribución-CompartirIgual
• trazado de rayos. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/ray_tracing. Licencia: CC BY-SA: Atribución-CompartirIgual
• punto focal. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/focal_point. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Diagramas de rayos, lente cóncava y espejo convexo. Ubicado en: http://www.youtube.com/watch?v=c2GFG6cvPew. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Aproximación de lente fina. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Thin_Lens_Aproximación. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ampliación. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Magnificación%23Calculando_la_magnificación_de_sistemas ópticos. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/definición/image-distancia. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/'final-lens-equation. Licencia: CC BY-SA: Atribución-CompartirIgual
• magnificación. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/magnification. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Diagramas de rayos, lente cóncava y espejo convexo. Ubicado en: http://www.youtube.com/watch?v=c2GFG6cvPew. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 30 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Ecuaciones de Lente Delgada para Lente Convexa. Ubicado en: http://www.youtube.com/watch?v=u4zhWFALZ-Q. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Acromático. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Achromat. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42292/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Doblete (lente). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/DoubleT_ (lente). Licencia: CC BY-SA: Atribución-CompartirIgual
• Lente (óptica). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lens_ (óptica) %23Lentes compuestos. Licencia: CC BY-SA: Atribución-CompartirIgual
• aberración. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/aberration. Licencia: CC BY-SA: Atribución-CompartirIgual
• doblete acromático. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Acromatic%20Doublet. Licencia: CC BY-SA: Atribución-CompartirIgual
• sistema afocal. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Afocal%20System. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Diagramas de rayos, lente cóncava y espejo convexo. Ubicado en: http://www.youtube.com/watch?v=c2GFG6cvPew. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 30 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Ecuaciones de Lente Delgada para Lente Convexa. Ubicado en: http://www.youtube.com/watch?v=u4zhWFALZ-Q. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 6 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42292/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Telescopio refractario. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Telescopio Refracting_. Licencia: Dominio Público: No Conocido Derechos de Autor
• Ecuación de Lensmaker. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lensmaker's_ecuation%23Lensmaker.27s_ecuation. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/fsic/c/thick-lens. Licencia: CC BY-SA: Atribución-CompartirIgual
• vértices de superficie. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Surface%20Vertices. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Diagramas de rayos, lente cóncava y espejo convexo. Ubicado en: http://www.youtube.com/watch?v=c2GFG6cvPew. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 30 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Ecuaciones de Lente Delgada para Lente Convexa. Ubicado en: http://www.youtube.com/watch?v=u4zhWFALZ-Q. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 6 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42292/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Telescopio refractario. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Refracting_telescope. Licencia: Dominio Público: No Conocido Derechos de Autor
• Ecuación de Lensmaker. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lensmaker's_ecuation%23Lensmaker.27s_ecuation. Licencia: Dominio Público: No Conocido Derechos de Autor
• Ecuación de Lensmaker. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lensmaker's_ecuation%23Lensmaker.27s_ecuation. Licencia: Dominio Público: No Conocido Derechos de Autor
• Refracción. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Refracción. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Lente (óptica). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lens_ (óptica). Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/fsic/c/concave-lens. Licencia: CC BY-SA: Atribución-CompartirIgual
• lente convexa. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/convex_lens. Licencia: CC BY-SA: Atribución-CompartirIgual
• punto focal. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/focal_point. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Colegio OpenStax, Formación de Imagen por Lentes. 29 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/#import-auto-id1625442. Licencia: CC BY: Atribución
• Diagramas de rayos, lente cóncava y espejo convexo. Ubicado en: http://www.youtube.com/watch?v=c2GFG6cvPew. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 30 de diciembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Ecuaciones de Lente Delgada para Lente Convexa. Ubicado en: http://www.youtube.com/watch?v=u4zhWFALZ-Q. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 6 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42292/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Telescopio refractario. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Refracting_telescope. Licencia: Dominio Público: No Conocido Derechos de Autor
• Ecuación de Lensmaker. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lensmaker's_ecuation%23Lensmaker.27s_ecuation. Licencia: Dominio Público: No Conocido Derechos de Autor
• Ecuación de Lensmaker. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Lensmaker's_ecuation%23Lensmaker.27s_ecuation. Licencia: Dominio Público: No Conocido Derechos de Autor
• Colegio OpenStax, Colegio de Física. 1 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42470/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución