24.4: Espejos

Última actualización
Guardar como PDF

Page ID: 127832

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

objetivos de aprendizaje

Describir la interacción de la luz con una superficie de espejo

Espejos Planos y Reflexión

Un espejo es una superficie reflectante que no permite el paso de la luz y en su lugar la rebota, produciendo así una imagen. Los espejos más comunes son planos y se llaman espejos planos. Estos espejos están hechos poniendo una fina capa de nitrato de plata o aluminio detrás de una pieza plana de vidrio.

Cuando colocas un objeto frente a un espejo, ves una imagen del mismo objeto en el espejo. El objeto es la fuente de los rayos incidentes, y la imagen está formada por los rayos reflejados. Una imagen formada por reflexión puede ser real o virtual. Una imagen “real” ocurre cuando los rayos de luz en realidad se cruzan con la imagen, y se vuelven invertidos, o al revés. Una imagen “virtual” ocurre cuando los rayos de luz no se encuentran realmente en la imagen. En cambio, “ves” la imagen porque tu ojo proyecta rayos de luz hacia atrás. ¡Te engaña para que veas una imagen! Una imagen virtual está a la derecha hacia arriba (vertical).

En espejos planos, o planos, la imagen es una imagen virtual, y está a la misma distancia detrás del espejo que el objeto está frente al espejo. La imagen también tiene el mismo tamaño que el objeto. Estas imágenes también son de paridad invertida, lo que significa que tienen una inversión izquierda-derecha.

Diagramas de rayos

La forma en que podemos predecir cómo se verá una reflexión es dibujando un diagrama de rayos. Estos diagramas se pueden utilizar para encontrar la posición y el tamaño de la imagen y si esa imagen es real o virtual. Estos son los pasos que sigue para dibujar un diagrama de rayos:

Dibuja el espejo plano como una línea recta sobre un eje principal. El eje principal es una línea imaginaria que se dibuja perpendicular al espejo.
Dibuja el objeto como una flecha frente al espejo.
Dibuja la imagen del objeto, utilizando el principio de que la imagen se coloca a la misma distancia detrás del espejo que el objeto está frente al espejo. El tamaño de la imagen es también el mismo que el tamaño del objeto. muestra estos tres primeros pasos.
Coloca un punto en el punto en el que se encuentra el ojo.
Escoge un punto en la imagen y dibuja el rayo reflejado que viaja al ojo como ve este punto. Recuerda agregar una punta de flecha.
Dibujar el rayo incidente para la luz que viaja desde el punto correspondiente sobre el objeto hasta el espejo, de tal manera que se obedece la ley de la reflexión.
Continuar por otros puntos extremos en el objeto (es decir, la punta y la base de la flecha). Un diagrama de rayos completo se muestra en

El ángulo en el que un rayo de luz incide sobre el espejo es el mismo ángulo en el que se reflejará de nuevo. Si, por ejemplo, un rayo de luz deja la parte superior de un objeto viajando paralelo al eje principal, golpeará el espejo en un ángulo de 0 grados, y se reflejará de nuevo a 0 grados. Cuando esto sucede, decimos que el rayo choca con normalidad en el espejo. Si el rayo de luz golpea el objeto en un ángulo de 30 grados, se reflejará de nuevo en un ángulo de 30 grados.

Formación de imágenes por espejos esféricos: convenciones de reflexión y signos

Un espejo es una superficie reflectante por la que no pasa la luz, hecha por una capa de nitrato de plata o aluminio detrás de una pieza de vidrio.

objetivos de aprendizaje

Distinguir las propiedades de los espejos cóncavos y convexos

Visión general

Un espejo es una superficie reflectante por la que la luz no pasa, sino que rebota y esto produce una imagen. Los espejos se hacen poniendo una fina capa de nitrato de plata o aluminio detrás de una pieza plana de vidrio.

Cuando colocas un objeto frente a un espejo, ves el mismo objeto en el espejo. Esta imagen que parece estar detrás del espejo se llama la imagen. El objeto es la fuente de los rayos incidentes, y la imagen está formada por los rayos reflejados. Una imagen formada por reflexión puede ser real o virtual. Una imagen real ocurre cuando los rayos de luz realmente se cruzan con la imagen, y se invierte, o al revés. Una imagen virtual ocurre cuando los rayos de luz no se encuentran realmente en la imagen. En cambio, “ves” la imagen porque tu ojo proyecta rayos de luz hacia atrás. Una imagen virtual está a la derecha hacia arriba (vertical).

Esta sección cubrirá los espejos esféricos. Los espejos esféricos pueden ser cóncavos o convexos. El centro de curvatura es el punto en el centro de la esfera y describe cuán grande es la esfera. Estos conceptos se muestran en.

imagen

Espejos Esféricos: Esta figura muestra la diferencia entre un espejo cóncavo y convexo.

Espejos cóncavos

En un espejo cóncavo, el eje principal es una línea que es perpendicular al centro del espejo. La forma más fácil de visualizar cómo se verá una imagen en este tipo de espejo es un diagrama de rayos. Antes de que eso se pueda hacer, primero se debe definir el punto focal. Este punto se encuentra a medio camino entre el espejo y el centro de curvatura en el eje principal. La distancia al punto focal desde el espejo se llama distancia focal. Podemos ver por la figura que esta distancia focal también es igual a la mitad del radio de la curvatura. muestra el diagrama de rayos de un espejo cóncavo.

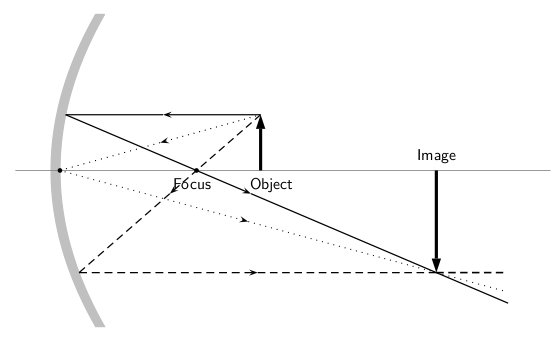
imagen

Diagrama de rayos cóncavos: Este es un diagrama de rayos de un espejo cóncavo Los pasos dados para dibujar son los mismos que los de un espejo plano.

A continuación se muestra un resumen de las propiedades de los espejos cóncavos:

convergente
imagen real
invertida
imagen delante del espejo

Espejos convexos

En los espejos convexos, el eje principal es el mismo que en un espejo plano o cóncavo, perpendicular al centro del espejo. En este caso, el punto focal está detrás del espejo. Un espejo convexo tiene una distancia focal negativa debido a esto. El punto focal está a la misma distancia del espejo que en un espejo cóncavo. Esto se muestra en.

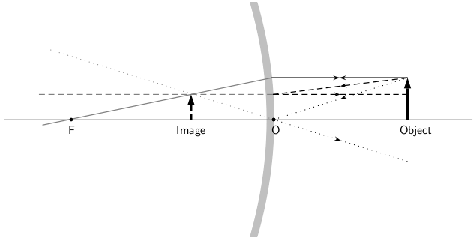
imagen

Diagrama de rayos de espejo convexo: Un espejo convexo con tres rayos dibujados para ubicar la imagen. Cada rayo incidente se refleja de acuerdo con la Ley de Reflexión. Los rayos reflejados divergen. Si los rayos reflejados se extienden detrás del espejo, entonces su intersección da la ubicación de la imagen detrás del espejo. Para un espejo convexo, la imagen es virtual y vertical.

A continuación se muestra un resumen de las propiedades de los espejos convexos:

divergente
imagen virtual
vertical
imagen detrás del espejo

Puntos Clave

Las imágenes reflejadas pueden ser reales o virtuales. En un espejo plano, las imágenes son virtuales.
Las imágenes virtuales en un espejo plano tienen una inversión izquierda-derecha.
Dibujar un diagrama de rayos es una forma de predecir cómo se verá una imagen reflejada.
Las imágenes en espejos pueden ser reales o virtuales.
A continuación se muestra un resumen de las propiedades de los espejos cóncavos: convergente imagen real invertida frente al espejo.
A continuación se muestra un resumen de las propiedades de los espejos convexos: imagen virtual divergente imagen vertical detrás del espejo.

Términos Clave

imagen virtual: Una imagen virtual ocurre cuando los rayos de luz no se encuentran realmente en la imagen
cóncavo: curvado como la superficie interna de una esfera o cuenco
convexo: curvado o inclinado hacia afuera como el exterior de un cuenco o esfera o círculo

Search

Text Color

Text Size

Margin Size

Font Type