Saltar al contenido principal
LibreTexts Español

26.1: Superposición e interferencia

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    127829

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Contraste los efectos de la interferencia constructiva y destructiva

    Condiciones para la interferencia de onda

    La interferencia es un fenómeno en el que dos ondas se superponen para formar una onda resultante de mayor o menor amplitud. Sus efectos se pueden observar en todo tipo de ondas (por ejemplo, luz, ondas acústicas y ondas de agua). La interferencia generalmente se refiere a la interacción de ondas que están correlacionadas (coherentes) entre sí porque se originan de la misma fuente, o tienen la misma o casi la misma frecuencia. Cuando dos o más ondas inciden en un mismo punto, el desplazamiento total en ese punto es igual a la suma vectorial de los desplazamientos de las ondas individuales. Si una cresta de una onda se encuentra con una cresta de otra onda de la misma frecuencia en el mismo punto, entonces la magnitud del desplazamiento es la suma de las magnitudes individuales. Esto es interferencia constructiva y ocurre cuando la diferencia de fase entre las ondas es un múltiplo de 2π. La interferencia destructiva ocurre cuando la cresta de una ola se encuentra con un canal de otra onda. En este caso, la magnitud de los desplazamientos es igual a la diferencia en las magnitudes individuales, y ocurre cuando esta diferencia es un múltiplo impar de π. Ejemplos de interferencia constructiva y destructiva se muestran en. Si la diferencia entre las fases es intermedia entre estos dos extremos, entonces la magnitud del desplazamiento de las ondas sumadas se encuentra entre los valores mínimo y máximo.

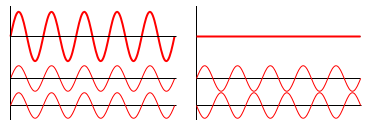
    imagen

    Interferencia de Onda: Ejemplos de interferencia de onda constructiva (izquierda) y destructiva (derecha).

    Interferencia de Onda: Una breve introducción a la interferencia de ondas constructivas y destructivas y al principio de superposición.

    Se observa una forma simple de interferencia de onda cuando dos ondas de la misma frecuencia (también llamada onda plana) se cruzan en ángulo, como se muestra en. Suponiendo que las dos ondas están en fase en el punto B, entonces la fase relativa cambia a lo largo del eje x. La diferencia de fase en el punto A viene dada por:

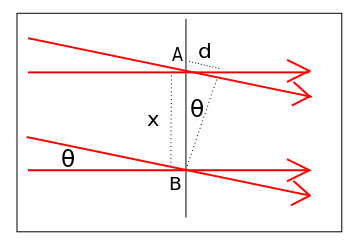
    imagen

    Interferencia de Ondas Planas: Disposición geométrica para interferencia de dos ondas planas.

    \[\Delta \varphi = \dfrac { 2 \pi \mathrm { d } } { \lambda } = \frac { 2 \pi \mathrm { x } \sin \theta } { \lambda }\]

    La interferencia constructiva ocurre cuando las ondas están en fase, o

    \[\dfrac { x \sin \theta } { \lambda } = 0 , \pm 1 , \pm 2 , \ldots \]

    La interferencia destructiva ocurre cuando las ondas están desfasadas medio ciclo, o

    \[\dfrac { x \sin \theta } { \lambda } = \pm \frac { 1 } { 2 } , \pm \frac { 3 } { 2 } , \ldots\]

    Reflexión por cambio de fase

    La luz exhibe características de onda en diversos medios así como en vacío. Cuando la luz pasa de un vacío a algún medio (como el agua) su velocidad y longitud de onda cambian, pero su frecuencia f sigue siendo la misma. La velocidad de la luz en un medio es v = c/n, donde n es el índice de refracción. Por ejemplo, el agua tiene un índice de refracción de n = 1.333. Cuando la luz se refleja en un medio con un índice de refracción más alto, las crestas se reflejan a medida que los abrevaderos y los canales se reflejan como crestas. En otras palabras, la onda sufre un cambio de fase de 180 grados tras la reflexión, y el rayo reflejado “salta” hacia adelante en media longitud de onda.

    Cuña de aire

    Una cuña de aire es un interferómetro simple que se utiliza para visualizar la perturbación del frente de onda después de la propagación a través de un objeto de prueba.

    objetivos de aprendizaje

    • Describir cómo se usa una cuña de aire para visualizar la perturbación de un frente de ola después de la proagación

    Cuña de aire

    Una cuña de aire es uno de los diseños más simples de interferómetros de cizallamiento utilizados para visualizar la perturbación del frente de onda después de la propagación a través de un objeto de prueba. Se puede usar una cuña de aire con casi cualquier fuente de luz, incluida la luz blanca no coherente. El interferómetro consiste en dos cuñas de vidrio óptico (~2-5 grados), empujadas juntas y luego ligeramente separadas de un lado para crear una cuña delgada de entrehierro. Un ejemplo de un interferómetro de cuña de aire se muestra en.

    imagen

    Cuña de aire: Ejemplo de interferómetro de cuña de aire

    El espacio de aire entre las dos placas de vidrio tiene dos propiedades únicas: es muy delgado (escala micrométrica) y tiene una planitud perfecta. Debido a este espacio de aire extremadamente delgado, el interferómetro de cuña de aire se ha utilizado con éxito en experimentos con láseres de alta potencia de femto-segundos.

    Un haz de luz incidente encuentra cuatro límites en los que cambia el índice de refracción de los medios, provocando cuatro haces reflejados (o reflejos de Fresnel) como se muestra en. La primera reflexión se produce cuando el haz entra en la primera placa de vidrio. La segunda reflexión ocurre cuando la viga sale de la primera placa y entra en la cuña de aire, y la tercera reflexión ocurre cuando la viga sale de la cuña de aire y entra en la segunda placa de vidrio. El cuarto haz se refleja cuando se encuentra con el límite de la segunda placa de vidrio. El ángulo de cuña de aire, entre la segunda y tercera reflexiones de Fresnel, se puede ajustar, haciendo que los haces de luz reflejados interfieran constructiva y destructivamente y creen un patrón de flecos. Para minimizar las aberraciones de imagen de las franjas resultantes, el plano angular de las cuñas de vidrio debe colocarse ortogonal al plano angular de la cuña de aire.

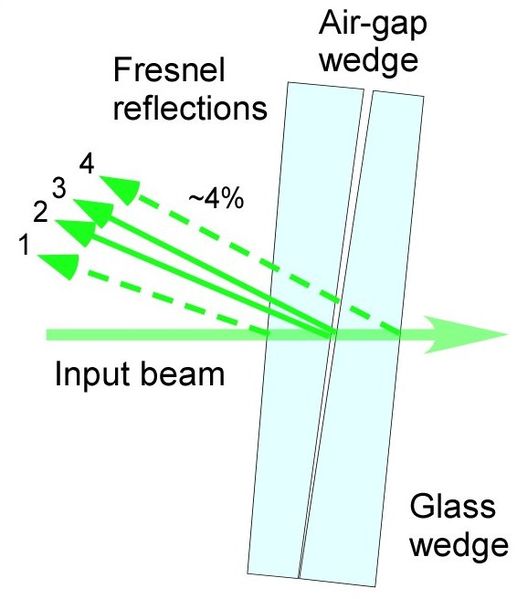
    imagen

    Reflejos de la luz dentro de un interferómetro de cuña de aire: trayectoria del haz dentro del interferómetro de cuña

    Anillos de Newton

    Los anillos de Newton son una serie de círculos concéntricos centrados en el punto de contacto entre una superficie esférica y una superficie plana.

    objetivos de aprendizaje

    • Aplicar anillos de Newton para determinar las características de luz de una lente

    Anillos de Newton

    En 1717, Isaac Newton analizó por primera vez un patrón de interferencia causado por el reflejo de la luz entre una superficie esférica y una superficie plana adyacente. Aunque fue observado por primera vez por Robert Hooke en 1664, este patrón se llama anillos de Newton, ya que Newton fue el primero en analizar y explicar los fenómenos. Los anillos de Newton aparecen como una serie de círculos concéntricos centrados en el punto de contacto entre las superficies esféricas y planas. Cuando se ven con luz monocromática, los anillos de Newton aparecen como anillos alternantes brillantes y oscuros; cuando se ven con luz blanca, se observa un patrón de anillos concéntricos de colores arcoíris. Un ejemplo de los anillos de Newton cuando se ven con luz blanca se muestra en la siguiente figura.

    imagen

    Anillos de Newton en una gota de agua: Anillos de Newton vistos en dos lentes plano-convexas con sus superficies planas en contacto. Una superficie es ligeramente convexa, creando los anillos. En luz blanca, los anillos son de color arcoíris, debido a que las diferentes longitudes de onda de cada color interfieren en diferentes ubicaciones.

    Los anillos de luz son causados por la interferencia constructiva entre los rayos de luz reflejados desde ambas superficies, mientras que los anillos oscuros son causados por interferencia destructiva. Los anillos exteriores están más espaciados que los internos porque la pendiente de la superficie curva de la lente aumenta hacia afuera. El radio del anillo brillante enésimo viene dado por:

    \[\mathrm { r } _ { \mathrm { N } } = \left[ \left( \mathrm { N } - \dfrac { 1 } { 2 } \lambda \mathrm { R } \right) \right] ^ { 1 / 2 }\]

    donde N es el número de anillo brillante, R es el radio de curvatura de la lente por la que pasa la luz, y λ es la longitud de onda de la luz que pasa a través del vidrio.

    Se coloca una lente esférica en la parte superior de una superficie de vidrio plana. Un rayo de luz incidente pasa a través de la lente curva hasta llegar al límite vidrio-aire, momento en el que pasa de una región de mayor índice de refracción n (el vidrio) a una región de menor n (aire). En este límite, algo de luz se transmite al aire, mientras que algo de luz se refleja. La luz que se transmite al aire no experimenta un cambio de fase y recorre una distancia, d, antes de que se refleje en la superficie plana de vidrio inferior. Este segundo límite de aire-vidrio imparte un desplazamiento de fase de medio ciclo al rayo de luz reflejado porque el aire tiene un n menor que el vidrio. Los dos rayos de luz reflejados ahora viajan en la misma dirección para ser detectados. A medida que uno se aleja del punto en el que las dos superficies se tocan, la distancia d aumenta porque la lente se curva alejándose de la superficie plana.

    imagen

    Formación de franjas de interferencia: Esta figura muestra cómo se forman las franjas de interferencia.

    Si la diferencia de longitud de trayectoria entre los dos haces de luz reflejados es un múltiplo impar de la longitud de onda dividido por dos, λ /2, las ondas reflejadas estarán 180 grados fuera de fase e interferirán destructivamente, causando una franja oscura. Si la diferencia de longitud de trayectoria es un múltiplo par de λ /2, las ondas reflejadas estarán en fase entre sí. La interferencia constructiva de las dos ondas reflejadas crea una franja brillante.

    Puntos Clave

    • Cuando dos o más ondas inciden en un mismo punto, el desplazamiento total en ese punto es igual a la suma vectorial de los desplazamientos de las ondas individuales.
    • La luz exhibe características de onda en diversos medios así como en vacío. Cuando la luz pasa de un vacío a algún medio, como el agua, su velocidad y longitud de onda cambian, pero su frecuencia f sigue siendo la misma.
    • Cuando la luz se refleja en un medio con un índice de refracción más alto, las crestas se reflejan a medida que los abrevaderos y los canales se reflejan como crestas. En otras palabras, la onda sufre un cambio de fase de 180 grados tras la reflexión, y el rayo reflejado “salta” hacia adelante en media longitud de onda.
    • Un interferómetro de cuña de aire consiste en dos cuñas de vidrio óptico (~2-5 grados), empujadas juntas y luego ligeramente separadas de un lado para crear una cuña delgada de espacio de aire.
    • El espacio de aire entre las dos placas de vidrio tiene dos propiedades únicas: es muy delgado (escala micrométrica) y tiene una planitud perfecta.
    • Para minimizar las aberraciones de imagen de las franjas resultantes, el plano angular de las cuñas de vidrio debe colocarse ortogonal al plano angular de la cuña de aire.
    • Cuando se ven con luz monocromática, los anillos de Newton aparecen como anillos alternantes brillantes y oscuros; cuando se ven con luz blanca, se observa un patrón de anillos concéntricos de colores arcoíris.
    • Si la diferencia de longitud de trayectoria entre los dos haces de luz reflejados es un múltiplo impar de la longitud de onda dividido por dos, λ/2, las ondas reflejadas estarán 180 grados fuera de fase e interferirán destructivamente, causando una franja oscura.
    • Si la diferencia de longitud de trayectoria es un múltiplo par de λ/2, las ondas reflejadas estarán en fase entre sí. La interferencia constructiva de las dos ondas reflejadas crea una franja brillante.

    Términos Clave

    • coherente: De ondas que tienen la misma dirección, longitud de onda y fase, que la luz en un láser.
    • onda plana: Una onda de frecuencia constante cuyos frentes de onda (superficies de fase constante) son planos paralelos infinitos de amplitud pico a pico constante normal al vector de velocidad de fase.
    • ortogonal: De dos objetos, en ángulo recto; perpendiculares entre sí.
    • interferómetro: Cualquiera de varios instrumentos que utilizan la interferencia de las ondas para determinar longitudes de onda y velocidades de onda, determinar índices de refracción y medir pequeñas distancias, cambios de temperatura, tensiones y muchas otras mediciones útiles.
    • longitud de onda: La longitud de un solo ciclo de una onda, medida por la distancia entre un pico o canal de una onda y el siguiente; a menudo se designa en física como λ, y corresponde a la velocidad de la onda dividida por su frecuencia.
    • lente: un objeto, generalmente hecho de vidrio, que enfoca o desenfoca la luz que pasa a través de él
    • monocromático: Describe un haz de luz con una sola longitud de onda (es decir, de un color o frecuencia específicos).

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    26.1: Superposición e interferencia is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.