26.2: Difracción

objetivos de aprendizaje

• Formular el principio de Huygens

Visión general

El principio Huygens-Fresnel establece que cada punto en un frente de onda es una fuente de ondículas. Estas ondículas se extienden en la dirección hacia adelante, a la misma velocidad que la onda fuente. El nuevo frente de onda es una línea tangente a todas las ondículas.

Antecedentes

Christiaan Huygens fue un científico holandés que desarrolló una técnica útil para determinar cómo y dónde se propagan las olas. En 1678, propuso que cada punto que toca una perturbación luminosa se convierta en fuente de una onda esférica. La suma de las ondas secundarias (ondas que son resultado de la perturbación) determina la forma de la nueva onda. muestra ondas secundarias viajando hacia adelante desde su punto de origen. Pudo llegar a una explicación de la propagación de ondas lineales y esféricas, y derivar las leyes de reflexión y refracción (cubiertas en átomos anteriores) utilizando este principio. No pudo, sin embargo, explicar lo que comúnmente se conoce como efectos de difracción. Los efectos de difracción son las desviaciones de la propagación rectilínea que ocurre cuando la luz se encuentra con bordes, pantallas y aberturas. Estos efectos fueron explicados en 1816 por el físico francés Augustin-Jean Fresnel.

Frente de onda recto: principio de Huygens aplicado a un frente de onda recto. Cada punto en el frente de onda emite una ondícula semicircular que se mueve una distancia s=vt. El nuevo frente de onda es una línea tangente a las ondículas.

Principio de Huygens

La Figura 1 muestra un ejemplo sencillo del Principio de Difracción de Huygens. El principio se puede mostrar con la siguiente ecuación:

\[\mathrm { s } = \mathrm { v } \mathrm { t }\]

donde s es la distancia, v es la velocidad de propagación y t es el tiempo.

Cada punto en el frente de onda emite una onda a velocidad, v. Las ondas emitidas son semicirculares, y ocurren a t, tiempo después. El nuevo frente de onda es tangente a las ondículas. Este principio funciona para todos los tipos de onda, no solo para las ondas de luz. El principio es útil para describir la reflexión, la refracción y la interferencia. muestra visualmente cómo se puede usar el Principio de Huygens para explicar la reflexión, y muestra cómo se puede aplicar a la refracción.

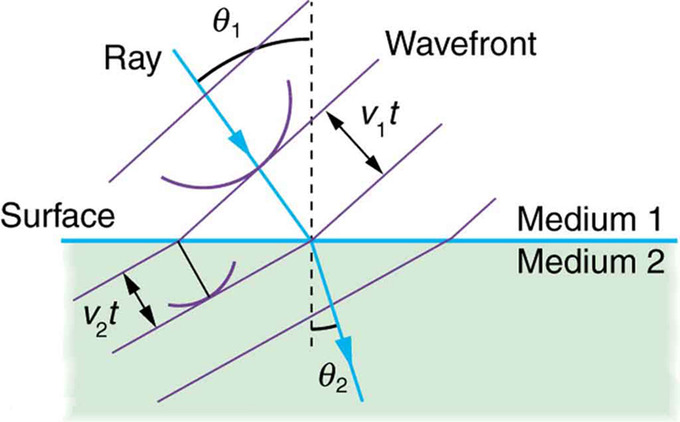
Refracción de Huygens: principio de Huygens aplicado a un frente de onda recto que viaja de un medio a otro donde su velocidad es menor. El rayo se dobla hacia la perpendicular, ya que las ondículas tienen una velocidad menor en el segundo medio.

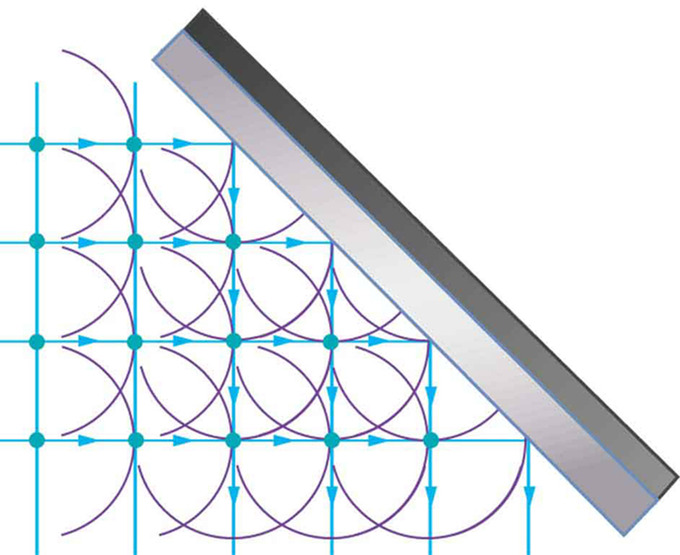
Reflexión: El principio de Huygens aplicado a un frente de onda recto golpeando un espejo. Las ondículas mostradas se emitieron a medida que cada punto en el frente de onda golpeó el espejo. La tangente a estas ondículas muestra que el nuevo frente de onda se ha reflejado en un ángulo igual al ángulo incidente. La dirección de propagación es perpendicular al frente de onda, como lo muestran las flechas que apuntan hacia abajo.

Ejemplo\(\PageIndex{1}\):

Este principio es en realidad algo que has visto o experimentado a menudo, pero simplemente no te das cuenta. Si bien este principio se aplica a todo tipo de ondas, es más fácil de explicar usando ondas sonoras, ya que las ondas sonoras tienen longitudes de onda más largas. Si alguien está tocando música en su habitación, con la puerta cerrada, es posible que no puedas oírla mientras pasas por la habitación. Sin embargo, si esa persona donde abrir su puerta mientras toca música, se puede escuchar no sólo cuando directamente frente a la apertura de la puerta, sino también a una distancia considerable abajo del pasillo a cada lado. Es un efecto directo de difracción. Cuando la luz pasa a través de aberturas mucho más pequeñas, llamadas hendiduras, el principio de Huygens muestra que la luz se dobla de manera similar a la forma en que lo hace el sonido, solo en una escala mucho menor. Examinaremos en átomos posteriores la difracción de rendija simple y la difracción de doble rendija, pero por ahora solo es importante que entendamos el concepto básico de difracción.

Difracción

Como explicamos en el párrafo anterior, la difracción se define como la flexión de una onda alrededor de los bordes de una abertura o un obstáculo.

Experimento de doble raja de Young

El experimento de doble rendija, también llamado experimento de Young, muestra que la materia y la energía pueden mostrar características tanto de onda como de partículas.

objetivos de aprendizaje

• Explicar por qué el experimento de Young es más creíble que el de Huygens

El experimento de doble rendija, también llamado experimento de Young, muestra que la materia y la energía pueden mostrar características tanto de onda como de partículas. Como discutimos en el átomo sobre el principio Huygens, Christiaan Huygens demostró en 1628 que la luz era una onda. Pero algunas personas no estaban de acuerdo con él, sobre todo Isaac Newton. Newton consideró que los efectos de color, interferencia y difracción necesitaban una mejor explicación. La gente no aceptó la teoría de que la luz era una ola hasta 1801, cuando el físico inglés Thomas Young realizó su experimento de doble rendija. En su experimento, envió luz a través de dos hendiduras verticales muy próximas y observó el patrón resultante en la pared detrás de ellas. El patrón que resultó se puede ver en.

Experimento de doble hendidura de Young: La luz se envía a través de dos ranuras verticales y se difracta en un patrón de líneas verticales extendidas horizontalmente. Sin difracción e interferencia, la luz simplemente haría dos líneas en la pantalla.

Dualidad Onda-Partícula

Las características de onda de la luz hacen que la luz pase a través de las hendiduras e interfiera consigo misma, produciendo las áreas claras y oscuras en la pared detrás de las hendiduras. La luz que aparece en la pared detrás de las hendiduras es dispersada y absorbida por la pared, que es característica de una partícula.

Experimento de Young

¿Por qué el experimento de Young fue mucho más creíble que el de Huygens? Porque, si bien Huygens tenía razón, no pudo demostrar que la luz actuara como una onda, mientras que el experimento de doble rendija lo demuestra muy claramente. Dado que la luz tiene longitudes de onda relativamente cortas, para mostrar los efectos de onda debe interactuar con algo pequeño: las pequeñas hendiduras de Young, poco espaciadas funcionaron.

El ejemplo en utiliza dos fuentes de luz coherentes de una sola longitud de onda monocromática para simplificar. (Esto significa que las fuentes de luz estaban en la misma fase.) Las dos hendiduras hacen que las dos fuentes de luz coherentes interfieran entre sí ya sea constructiva o destructivamente.

Interferencia de ondas constructivas y destructivas

La interferencia constructiva de las olas ocurre cuando las ondas interfieren entre sí de cresta a cresta (pico a pico) o canal a valle (valle a valle) y las olas están exactamente en fase entre sí. Esto amplifica la onda resultante. La interferencia destructiva de las ondas ocurre cuando las ondas interfieren entre sí de cresta a valle (pico a valle) y están exactamente desfasadas entre sí. Esto cancela cualquier onda y no da como resultado luz. Estos conceptos se muestran en. Cabe señalar que este ejemplo utiliza una sola longitud de onda monocromática, lo que no es común en la vida real; en el que se muestra un ejemplo más práctico.

Interferencia práctica de ondas constructivas y destructivas: Las rendijas dobles producen dos fuentes coherentes de ondas que interfieren. (a) La luz se extiende (difracta) de cada hendidura porque las hendiduras son estrechas. Estas ondas se superponen e interfieren constructivamente (líneas brillantes) y destructivamente (regiones oscuras). Esto sólo podemos ver si la luz cae sobre una pantalla y se dispersa en nuestros ojos. b) Los patrones de interferencia de doble rendija para las olas de agua son casi idénticos a los de la luz. La acción de las olas es mayor en regiones de interferencia constructiva y menos en regiones de interferencia destructiva. (c) Cuando la luz que ha pasado por hendiduras dobles cae sobre una pantalla, vemos un patrón como este.

Interferencia teórica constructiva y destructiva de ondas: Las amplitudes de las ondas se suman. (a) La interferencia constructiva pura se obtiene cuando ondas idénticas están en fase. (b) La interferencia destructiva pura ocurre cuando ondas idénticas están exactamente desfasadas (desplazadas en media longitud de onda).

El patrón que resulta de la difracción de doble rendija no es aleatorio, aunque puede parecer así. Cada hendidura está a una distancia diferente de un punto dado en la pared detrás de ella. Para cada distancia diferente, un número diferente de longitudes de onda encajan en esa trayectoria. Todas las olas comienzan en fase (emparejando cresta a cresta), pero dependiendo de la distancia del punto en la pared desde la hendidura, podrían estar en fase en ese punto e interferir constructivamente, o podrían terminar fuera de fase e interferir destructivamente entre sí.

Rejillas de Difracción: Rayos X, Rejilla, Reflexión

La rejilla de difracción tiene una estructura periódica que divide y difracta la luz en varios haces que viajan en diferentes direcciones.

objetivos de aprendizaje

• Describir la función de la rejilla de difracción

Rejilla de difracción

Una rejilla de difracción es un componente óptico con una estructura periódica que divide y difracta la luz en varios haces que viajan en diferentes direcciones. Las direcciones de estos haces dependen del espaciamiento de la rejilla y la longitud de onda de la luz para que la rejilla actúe como el elemento dispersivo. Debido a esto, las rejillas se utilizan a menudo en monocromadores, espectrómetros, dispositivos de multiplexación por división de longitud de onda, dispositivos de compresión de pulsos ópticos y muchos otros instrumentos ópticos.

Una diapositiva fotográfica con un patrón fino de líneas moradas forma una compleja rejilla. Para aplicaciones prácticas, las rejillas generalmente tienen crestas o reglas en su superficie en lugar de líneas oscuras. Dichas rejillas pueden ser transmisivas o reflectantes. También se producen rejillas que modulan la fase en lugar de la amplitud de la luz incidente, frecuentemente usando holografía.

Los medios de CD y DVD prensados ordinarios son ejemplos cotidianos de rejillas de difracción y se pueden usar para demostrar el efecto reflejando la luz solar sobre una pared blanca. (ver). Esto es un efecto secundario de su fabricación, ya que una superficie de un CD tiene muchos pequeños pozos en el plástico, dispuestos en espiral; esa superficie tiene una fina capa de metal aplicada para hacer los pozos más visibles. La estructura de un DVD es ópticamente similar, aunque puede tener más de una superficie deshuesada, y todas las superficies picadas están dentro del disco. En un disco de vinilo prensado estándar cuando se ve desde un ángulo bajo perpendicular a las ranuras, se puede ver un efecto similar, pero menos definido, al de un CD/DVD. Esto se debe al ángulo de visión (menor que el ángulo crítico de reflexión del vinilo negro) y la trayectoria de la luz que se refleja por ser cambiada por las ranuras, dejando atrás un patrón de relieve arcoíris.

Superficie legible de un CD: La superficie legible de un disco compacto incluye una pista en espiral enrollada lo suficientemente apretada como para hacer que la luz difracte en un espectro visible completo.

Algunas plumas de aves utilizan rejillas de difracción naturales que producen interferencia constructiva, dando a las plumas un efecto iridiscente. La iridiscencia es el efecto donde las superficies parecen cambiar de color cuando se cambia el ángulo de iluminación. Un ópalo es otro ejemplo de rejilla de difracción que refleja la luz en diferentes colores.

Difracción de rayos X

La cristalografía de rayos X es un método para determinar la estructura atómica y molecular de un cristal, en el que los átomos cristalinos hacen que un haz de rayos X difracte en muchas direcciones específicas. Al medir los ángulos e intensidades de estos haces difractados, un cristalógrafo puede producir una imagen tridimensional de la densidad de electrones dentro del cristal. A partir de esta densidad electrónica, se pueden determinar las posiciones medias de los átomos en el cristal, así como sus enlaces químicos, su desorden y otra información diversa.

En una medición de difracción de rayos X, se monta un cristal sobre un goniómetro y se gira gradualmente mientras se bombardea con rayos X, produciendo un patrón de difracción de puntos regularmente espaciados conocidos como reflexiones (ver). Las imágenes bidimensionales tomadas a diferentes rotaciones se convierten en un modelo tridimensional de la densidad de electrones dentro del cristal utilizando el método matemático de las transformadas de Fourier, combinado con datos químicos conocidos para la muestra.

Reflexiones en patrones de difracción: Cada punto, llamado reflejo, en este patrón de difracción se forma a partir de la interferencia constructiva de rayos X dispersos que pasan a través de un cristal. Los datos pueden ser utilizados para determinar la estructura cristalina.

Difracción de hendidura simple

La difracción de hendidura simple es el fenómeno que ocurre cuando las ondas pasan a través de un hueco estrecho y se doblan, formando un patrón de interferencia.

objetivos de aprendizaje

• Formular el principio de Huygens

Difracción

Como explicamos en un átomo anterior, la difracción se define como la flexión de una onda alrededor de los bordes de una abertura u obstáculo. La difracción es un fenómeno que todos los tipos de onda pueden experimentar. Se explica por el Principio Huygens-Fresnel, y el principio de superposición de olas. El primero afirma que cada punto en un frente de onda es una fuente de ondículas. Estas ondículas se extienden en la dirección hacia adelante, a la misma velocidad que la onda fuente. El nuevo frente de onda es una línea tangente a todas las ondículas. El principio de superposición establece que en cualquier momento, el resultado neto de múltiples estímulos es la suma de todos los estímulos.

Difracción de hendidura simple

En la difracción de hendidura simple, el patrón de difracción está determinado por la longitud de onda y por la longitud de la hendidura. La Figura 1 muestra una visualización de este patrón. Esta es la forma más simplista de usar el Principio Huygens-Fresnel, que estaba cubierto en un átomo anterior, y aplicarlo a la difracción de hendidura. Pero, ¿qué sucede cuando la hendidura NO es la longitud exacta (o cercana a la exacta) de una sola onda?

Difracción de hendidura simple: una longitud de onda: visualización de difracción de hendidura única cuando la hendidura es igual a una longitud de onda.

Una hendidura que es más ancha que una sola onda producirá efectos similares a interferencias aguas abajo de la hendidura. Es más fácil de entender pensando en la hendidura no como una hendidura larga, sino como una serie de fuentes puntuales espaciadas uniformemente a lo largo del ancho de la hendidura. Esto se puede ver en la Figura 2.

Difracción de hendidura simple: cuatro longitudes de onda: Esta figura muestra la difracción de una sola rendija, pero la ranura tiene una longitud de 4 longitudes de onda.

Para examinar mejor este efecto, consideremos una sola longitud de onda monocromática. Esto producirá un frente de onda que está todo en la misma fase. Aguas abajo de la hendidura, la luz en cualquier punto dado se compone de contribuciones de cada una de estas fuentes puntuales. Las diferencias de fase resultantes son causadas por las diferentes longitudes de trayectoria que las porciones contribuyentes de los rayos viajaron desde la hendidura.

La variación en la intensidad de onda se puede modelar matemáticamente. Desde el centro de la hendidura, las ondas difractantes se propagan radialmente. El ángulo de la intensidad mínima (θ _min) puede estar relacionado con la longitud de onda (λ) y el ancho de la hendidura (d) de tal manera que:

\[\mathrm { d } \sin \theta _ { \min } = \lambda\]

La intensidad (I) de las ondas en cualquier ángulo también se puede calcular como una relación con el ancho de la hendidura, la longitud de onda y la intensidad de las ondas originales antes de pasar por la hendidura:

\[\mathrm { I } ( \theta ) = \mathrm { I } _ { 0 } \left( \dfrac { \sin ( \pi \mathrm { x } ) } { \pi \mathrm { x } } \right) ^ { 2 }\]

donde x es igual a:

\[\dfrac { \mathrm { d } } { \lambda } \sin \theta\]

El criterio de Rayleigh

El criterio de Rayleigh determina el ángulo de separación entre dos fuentes de luz que son distinguibles entre sí.

objetivos de aprendizaje

• Explicar el significado del criterio de Rayleigh

Límites de Resolución

Junto con los efectos de difracción que hemos discutido en átomos anteriores, la difracción también limita el detalle que podemos obtener en las imágenes. muestra tres circunstancias diferentes de límites de resolución debido a la difracción:

Límites de resolución: a) La luz monocromática que pasa a través de una pequeña abertura circular produce este patrón de difracción. b) Dos fuentes puntuales de luz cercanas entre sí producen imágenes superpuestas debido a la difracción. c) Si están más cerca, no pueden resolverse ni distinguirse.

• (a) muestra una luz que pasa a través de una pequeña abertura circular. No se ve un contorno circular nítido, sino una mancha con bordes borrosos. Esto se debe a una difracción similar a la de una sola hendidura.
• (b) muestra dos fuentes puntuales juntas, produciendo imágenes superpuestas. Debido a la difracción, apenas se puede distinguir entre las dos fuentes puntuales.
• (c) muestra dos fuentes puntuales que están tan juntas que ya no se pueden distinguir entre ellas.

Este efecto se puede ver con la luz que pasa a través de pequeñas aberturas o aperturas más grandes. Este mismo efecto ocurre cuando la luz pasa por nuestras pupilas, y es por ello que el ojo humano tiene una agudeza limitada.

Criterio de Rayleigh

En el siglo XIX, Lord Rayleigh inventó un criterio para determinar cuándo dos fuentes de luz se distinguían entre sí, o se resolvían. Según los criterios, dos fuentes puntuales se consideran simplemente resueltas (lo suficientemente distinguibles entre sí para reconocer dos fuentes) si el centro del patrón de difracción de una se solapa directamente con el primer mínimo del patrón de difracción de la otra. Si la distancia es mayor entre estos puntos, las fuentes están bien resueltas (es decir, son fáciles de distinguir entre sí). Si la distancia es menor, no se resuelven (es decir, no se pueden distinguir entre sí). La ecuación para determinar esto es:

\[\theta = 1.22 \dfrac { \lambda } { \mathrm { D } }\]

θ — ángulo los objetos están separados por, en radián λ — longitud de onda de la luz D — diámetro de apertura. muestra este concepto visualmente. Esta ecuación también da la dispersión angular de una fuente de luz que tiene un diámetro D.

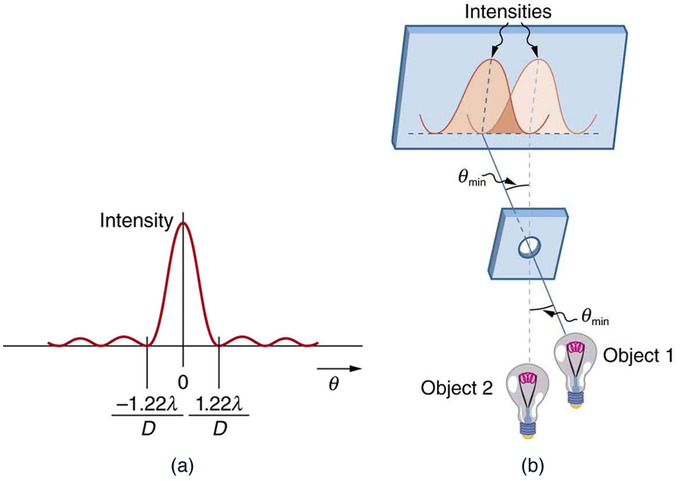
Criterio de Rayleigh: (a) Esta es una gráfica de intensidad del patrón de difracción para una abertura circular. Tenga en cuenta que, similar a una sola hendidura, el máximo central es más ancho y brillante que los de los lados. b) Dos objetos puntuales producen patrones de difracción superpuestos. Aquí se muestra el criterio de Rayleigh por ser simplemente resoluble. El máximo central de un patrón se encuentra en el primer mínimo del otro.

Puntos Clave

• La difracción es el concepto que se explica usando el Principio de Huygens, y se define como la flexión de una ola alrededor de los bordes de una abertura o un obstáculo.
• Este principio se puede utilizar para definir la reflexión, como se muestra en la figura. También se puede utilizar para explicar la refracción y la interferencia. Cualquier cosa que experimente este fenómeno es una ola. Al aplicar esta teoría a la luz que pasa por una hendidura, podemos demostrar que es una onda.
• El principio se puede mostrar con la siguiente ecuación: s=vt s — distancia v — velocidad de propagación t — tiempo Cada punto en el frente de onda emite una onda a velocidad, v. Las ondas emitidas son semicirculares, y ocurren en t, tiempo después. El nuevo frente de onda es tangente a las ondículas.
• Las características de onda de la luz hacen que la luz pase a través de las hendiduras e interfiera entre sí, produciendo las áreas claras y oscuras en la pared detrás de las hendiduras. La luz que aparece en la pared detrás de las hendiduras es parcialmente absorbida por la pared, característica de una partícula.
• La interferencia constructiva ocurre cuando las ondas interfieren entre sí de cresta a cresta y las ondas están exactamente en fase entre sí. La interferencia destructiva ocurre cuando las ondas interfieren entre sí de cresta a valle (pico a valle) y están exactamente desfasadas entre sí.
• Cada punto de la pared tiene una distancia diferente a cada hendidura; un número diferente de longitudes de onda encajan en esas dos trayectorias. Si las dos longitudes de trayectoria difieren en media longitud de onda, las ondas interferirán destructivamente. Si la longitud de la trayectoria difiere en una longitud de onda completa, las ondas interfieren constructivamente.
• Las direcciones de los haces difractados dependen del espaciamiento de la rejilla y la longitud de onda de la luz para que la rejilla actúe como elemento dispersivo.
• Las rejillas se utilizan comúnmente en monocromadores, espectrómetros, dispositivos de multiplexación por división de longitud de onda, dispositivos de compresión de pulsos ópticos y otros instrumentos ópticos.
• La difracción de rayos X se utiliza en cristalografía para producir la imagen tridimensional de la densidad de electrones dentro del cristal.
• El Principio de Huygens establece que cada punto en un frente de onda es una fuente de ondículas. Estas ondículas se extienden en la dirección hacia adelante, a la misma velocidad que la onda fuente. El nuevo frente de onda es una línea tangente a todas las ondículas.
• Si una hendidura es más larga que una sola longitud de onda, piense en ello como una serie de fuentes puntuales espaciadas uniformemente a través del ancho de la hendidura.
• Aguas abajo de una hendidura que es más larga que una sola longitud de onda, la luz en cualquier punto dado se compone de contribuciones de cada una de estas fuentes puntuales. Las diferencias de fase resultantes son causadas por las diferentes longitudes de trayectoria que las porciones contribuyentes de los rayos viajaron desde la hendidura.
• La difracción juega un papel importante en la resolución a la que podemos ver las cosas. Hay un punto donde dos fuentes de luz pueden estar tan cerca una de la otra que no podemos distinguirlas.
• Cuando dos fuentes de luz están cerca una de la otra, pueden ser: no resueltas (es decir, no capaces de distinguir una de la otra), simplemente resueltas (es decir, solo capaces de distinguirlas unas de otras), y un poco bien resueltas (es decir, fáciles de distinguir entre sí).
• Para que dos fuentes de luz se resuelvan, el centro de un patrón de difracción debe superponerse directamente con el primer mínimo del otro patrón de difracción.

Términos Clave

• difracción: La flexión de una onda alrededor de los bordes de una abertura o un obstáculo.
• interferencia constructiva: Ocurre cuando las olas interfieren entre sí cresta a cresta y las olas están exactamente en fase entre sí.
• interferencia destructiva: Ocurre cuando las olas interfieren entre sí de cresta a valle (pico a valle) y están exactamente desfasadas entre sí.
• interferencia: Un efecto causado por la superposición de dos sistemas de ondas, como una distorsión en una señal de difusión debido a efectos atmosféricos u otros efectos.
• iridiscencia: La condición o estado de ser iridiscente; exhibición de colores como los del arco iris; un juego prismático de color.
• difracción: La flexión de una onda alrededor de los bordes de una abertura o un obstáculo.
• monocromático: Describe un haz de luz con una sola longitud de onda (es decir, de un color o frecuencia específicos).
• resolución: El grado de finura con el que se puede grabar o producir una imagen, a menudo expresado como el número de píxeles por unidad de longitud (típicamente una pulgada).

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• OpenStax College, Principio de Huygens: Difracción. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• Huygensu2013Principio de Fresnel. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Huygens%e 2% 80% 93Fresnel_principle. Licencia: CC BY-SA: Atribución-CompartirIgual
• difracción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/diffraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• Experimento de doble rendija de Youngs. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Youngs_Double-slit_experiment. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/definition/ destructive-interferencia-. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/definitivo-interferencia-constructiva. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• Rejilla de difracción. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Diffraction_Grating. Licencia: CC BY-SA: Atribución-CompartirIgual
• Difracción de rayos X. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/X-Ray_Difracción. Licencia: CC BY-SA: Atribución-CompartirIgual
• Radiografías. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/X-rays. Licencia: CC BY-SA: Atribución-CompartirIgual
• Iridiscente. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Iridescent. Licencia: CC BY-SA: Atribución-CompartirIgual
• Difracción. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Difrfracción%23Difrfracción_Grating. Licencia: CC BY-SA: Atribución-CompartirIgual
• Rejilla de difracción. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Diffraction_Grating%23Natural_Gratings. Licencia: CC BY-SA: Atribución-CompartirIgual
• Cristalografía de rayos X. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/X-Ray_Cristalografía. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Difracción de hendidura múltiple. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42512/latest/. Licencia: CC BY: Atribución
• difracción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/diffraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• iridiscencia. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/iridiscence. Licencia: CC BY-SA: Atribución-CompartirIgual
• interferencia. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/interferencia.wiki/Interference Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• Patrón de difracción de rayos X 3clpro. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:X-Ray_Diffraction_Pattern_3clpro.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/d/d0/Compact_disc.svg/500px-compact_disc.svg.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Paul Padley, Difracción de hendidura simple. 18 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m12915/latest/. Licencia: CC BY: Atribución
• Difracción de hendidura simple. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Single_Slit_Diffracción%23Single-slit_diffraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/[/] monocromática. Licencia: CC BY-SA: Atribución-CompartirIgual
• difracción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/diffraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• Patrón de difracción de rayos X 3clpro. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:X-Ray_Diffraction_Pattern_3clpro.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/d/d0/Compact_disc.svg/500px-compact_disc.svg.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• WaveLongth=slitWidthSpectrum. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Wavelength=slitWidthSpectrum.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Difracción Onda 4Lambda Raja Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Onda_Difrfracción_4lambda_slit.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Criterio de Rayleigh. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Rayleigh_Criterion%23Explicación. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Límites de Resolución: El Criterio de Rayleigh. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42517/latest/. Licencia: CC BY: Atribución
• difracción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/diffraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• resolución. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/resolution. Licencia: CC BY-SA: Atribución-CompartirIgual
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Principio de Huygens: Difracción. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42505/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• OpenStax College, Youngu2019s Experimento de Doble Ranura. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42508/latest/. Licencia: CC BY: Atribución
• Patrón de difracción de rayos X 3clpro. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:X-Ray_Diffraction_Pattern_3clpro.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/d/d0/Compact_disc.svg/500px-compact_disc.svg.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• WaveLongth=slitWidthSpectrum. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Wavelength=slitWidthSpectrum.gif. Licencia: CC BY-SA: Atribución-CompartirIgual
• Difracción Onda 4Lambda Raja Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:Onda_Difrfracción_4lambda_slit.png. Licencia: Dominio Público: No Conocido Derechos de Autor
• OpenStax College, Límites de Resolución: El Criterio de Rayleigh. 12 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42517/latest/. Licencia: CC BY: Atribución
• OpenStax College, Límites de Resolución: El Criterio de Rayleigh. 11 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42517/latest/. Licencia: CC BY: Atribución