Saltar al contenido principal
LibreTexts Español

27.2: Consecuencias de la Relatividad Especial

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128448

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Formular conclusiones de la teoría de la relatividad especial, señalando los supuestos que se hicieron al derivarla

    La relatividad de la simultaneidad es el concepto de que la simultaneidad, ya sea que ocurran dos eventos al mismo tiempo, no es absoluta, sino que depende del marco de referencia del observador.

    Según la teoría de la relatividad especial, es imposible decir en sentido absoluto si dos eventos distintos ocurren al mismo tiempo si esos eventos están separados en el espacio, como un accidente automovilístico en Londres y otro en Nueva York. La cuestión de si los eventos son simultáneos es relativa: en algunos marcos de referencia los dos accidentes pueden ocurrir al mismo tiempo, en otros marcos (en un estado de movimiento diferente en relación con los eventos) el accidente en Londres puede ocurrir primero, y aún en otros fotogramas, el accidente de Nueva York puede ocurrir primero. Si los dos eventos están conectados causalmente (“el evento A causa el evento B”), entonces la relatividad de la simultaneidad preserva el orden causal (es decir, “el evento A causa el evento B” en todos los marcos de referencia).

    Si imaginamos que un marco de referencia asigna precisamente el mismo tiempo a dos eventos que se encuentran en diferentes puntos en el espacio, un marco de referencia que se mueve en relación con el primero generalmente asignará diferentes tiempos a los dos eventos. Esto se ilustra en la paradoja de la escalera, un experimento de pensamiento que utiliza el ejemplo de una escalera que se mueve a gran velocidad a través de un garaje.

    Una forma matemática de la relatividad de la simultaneidad (“hora local”) fue introducida por Hendrik Lorentz en 1892, e interpretada físicamente (a primer orden en v/c) como resultado de una sincronización usando señales de luz por Henri Poincaré en 1900. Sin embargo, tanto Lorentz como Poincaré basaron sus concepciones en el aether como marco de referencia preferido pero indetectable, y continuaron distinguiendo entre “tiempo verdadero” (en el éter) y tiempos “aparentes” para observadores en movimiento.

    En 1905, Albert Einstein abandonó el (clásico) etéreo y enfatizó la importancia de la relatividad de la simultaneidad para nuestra comprensión del espacio y el tiempo. Dedujo el fracaso de la simultaneidad absoluta a partir de dos supuestos declarados: 1) el principio de relatividad—la equivalencia de los marcos inerciales, tal que las leyes de la física se aplican por igual en todos los sistemas de coordenadas inerciales; 2) la constancia de la velocidad de la luz detectada en el espacio vacío, independiente de la movimiento relativo de su fuente.

    imagen

    Observador de pie sobre la plataforma: Marco de referencia de un observador parado en la plataforma (contracción de longitud no representada).

    imagen

    Observador a bordo del tren: El experimento de tren y plataforma a partir del marco de referencia de un observador a bordo del tren.

    Dilatación del tiempo

    La dilatación del tiempo es una diferencia real del tiempo transcurrido entre dos eventos medidos por observadores que se mueven uno con relación al otro.

    objetivos de aprendizaje

    • Explicar por qué la dilatación del tiempo puede ser ignorada en la vida diaria

    La dilatación del tiempo es una diferencia real del tiempo transcurrido entre dos eventos medidos por observadores que se mueven uno con relación al otro.

    Por ejemplo, dos cohetes (A y B) pasando a exceso de velocidad uno junto al otro en el espacio experimentarían dilatación en el tiempo. Si de alguna manera tuvieran una visión clara de los barcos del otro, cada tripulación vería los relojes y el movimiento de los demás como que iban demasiado despacio. Es decir, dentro del marco de referencia de la Nave A, todo se mueve normalmente, pero todo sobre la Nave B parece estar moviéndose más lento (y viceversa).

    Desde una perspectiva local, el tiempo registrado por relojes que están en reposo con respecto al marco de referencia local (y lejos de cualquier masa gravitacional) siempre parece pasar al mismo ritmo. Es decir, si un barco nuevo, el Barco C, viaja junto al Buque A, está “en reposo” relativo al Buque A. Desde el punto de vista del Buque A, el tiempo del nuevo Barco C también parecería normal.

    La fórmula para determinar la dilatación del tiempo es:\(\mathrm{\Delta t ^ { \prime } = \gamma \Delta t = \frac { \Delta t } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }}\)

    donde Δt es el intervalo de tiempo entre dos eventos co-locales (es decir, que ocurren en el mismo lugar) para un observador en algún marco inercial (por ejemplo, ticks en su reloj), esto se conoce como el tiempo adecuado, Δt' es el intervalo de tiempo entre esos mismos eventos, medido por otro observador, moviéndose inercialmente con velocidad v con respecto al observador anterior, v es la velocidad relativa entre el observador y el reloj en movimiento, c es la velocidad de la luz, y\(\mathrm{\gamma = \frac { 1 } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }}\)

    es el factor Lorentz. Así, se encuentra que la duración del ciclo de reloj de un reloj en movimiento se incrementa: se mide como “funcionando lento”. Tenga en cuenta que para velocidades inferiores a 1/10 la velocidad de la luz, el factor Lorentz es aproximadamente 1. Así, los efectos de dilatación del tiempo y extremadamente pequeños y pueden ser ignorados de manera segura en una vida diaria. Se vuelven importantes solo cuando un objeto se acerca a velocidades del orden de 30,000 km/s (1/10 la velocidad de la luz).

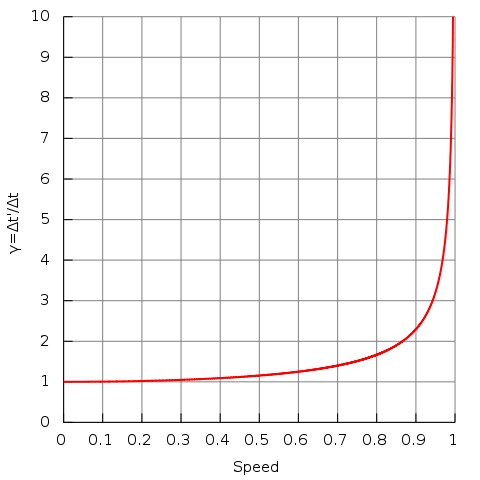
    imagen

    Factor Lorentz: Factor Lorentz en función de la velocidad (en unidades naturales donde c = 1). Observe que para velocidades pequeñas (menos de 0.1), γ es aproximadamente 1.

    Efectos de la dilatación del tiempo: La paradoja gemela y la decadencia del muón

    La paradoja de los gemelos es un experimento de pensamiento: un gemelo hace un viaje al espacio y regresa a casa para encontrar que el gemelo permaneció más envejecido.

    objetivos de aprendizaje

    • Explicar la paradoja gemela dentro del marco estándar de la relatividad especial

    La paradoja de los gemelos es un experimento mental en relatividad especial que involucra a gemelos idénticos, uno de los cuales realiza un viaje al espacio en un cohete de alta velocidad y regresa a casa para descubrir que el gemelo que permaneció en la Tierra ha envejecido más.

    Esto ocurre porque la relatividad especial muestra que cuanto más rápido viaja uno, más lento se mueve el tiempo para ellos.

    Este resultado parece desconcertante porque cada gemelo ve al otro gemelo viajando, y así, de acuerdo con una aplicación ingenua de dilatación del tiempo, cada uno debería encontrar paradójicamente que el otro haya envejecido más lentamente. Es decir, desde la perspectiva del cohete, la tierra se aleja del barco y desde la perspectiva de la tierra, el cohete se aleja.

    Sin embargo, este escenario puede resolverse dentro del marco estándar de la relatividad especial (porque los gemelos no son equivalentes; el gemelo espacial experimentó una aceleración asimétrica adicional al cambiar de dirección para regresar a casa), y por lo tanto no es una paradoja en el sentido de una contradicción lógica.

    La Tierra y la nave no están en una relación simétrica: independientemente de si vemos la situación desde la perspectiva de la Tierra o de la nave, la nave experimenta fuerzas de aceleración adicionales. La nave tiene un giro en el que acelera y cambia de dirección mientras que la tierra no. Como no hay simetría, no es paradójico que un gemelo sea más joven que el otro. Sin embargo, la paradoja gemela es útil como demostración de que la relatividad especial es autoconsistente.

    En el diagrama espacio-tiempo, dibujado para el marco de referencia del gemelo basado en la Tierra, la línea mundial de ese gemelo coincide con el eje vertical (su posición es constante en el espacio, moviéndose solo en el tiempo). En el primer tramo del viaje, el segundo gemelo se mueve hacia la derecha (línea inclinada negra); y en el de vuelta, de vuelta a la izquierda. Las líneas azules muestran los planos de simultaneidad para el gemelo viajero durante el primer tramo del viaje; líneas rojas, durante el segundo tramo. Justo antes del cambio, el gemelo viajero calcula la edad del gemelo basado en la Tierra midiendo el intervalo a lo largo del eje vertical desde el origen hasta la línea azul superior. Justo después del cambio, si recalcula, medirá el intervalo desde el origen hasta la línea roja inferior. En cierto sentido, durante el giro en U el plano de simultaneidad salta de azul a rojo y muy rápidamente barre sobre un gran segmento de la línea mundial del gemelo terrestre. El gemelo viajero reconoce que ha habido una discontinuidad de salto en la era del gemelo con base en la Tierra.

    imagen

    Diagrama espacio-tiempo de la paradoja gemela: diagrama espacio-tiempo de la paradoja gemela. El tiempo es relativo, pero ambos gemelos no son equivalentes (el barco experimenta aceleración adicional para cambiar la dirección de desplazamiento).

    Contracción de Longitud

    Los objetos que se mueven sufren una contracción de longitud a lo largo de la dimensión del movimiento; este efecto solo es significativo a velocidades relativistas.

    objetivos de aprendizaje

    • Explicar por qué la contracción de longitud puede ignorarse en la vida diaria

    La contracción de longitud es el fenómeno físico de una disminución en la longitud detectada por un observador de objetos que viajan a cualquier velocidad distinta de cero en relación con ese observador. La contracción de longitud surge debido a que la velocidad de la luz en un vacío es constante en cualquier marco de referencia. Al tomar esto en cuenta, así como algunas consideraciones geométricas, mostraremos cómo se ven afectados el tiempo y la duración percibidos.

    Ejemplo\(\PageIndex{1}\):

    Imaginemos un sencillo sistema de reloj que consta de dos espejos A y B en un vacío. Un pulso de luz rebota entre los dos espejos. La separación de los espejos es L, y el reloj marca una vez cada vez que el pulso de luz golpea un espejo dado. Ahora imagina que el reloj está en reposo. El tiempo que tardará el pulso de luz en pasar del espejo A al espejo B y luego de vuelta al espejo A puede describirse mediante:

    \[\Delta t = \dfrac { 2 \mathrm { L } } { c }\]

    donde c es la velocidad de la luz. Ahora imagina que el reloj se mueve en la dirección horizontal con relación a un observador estacionario. El pulso de luz se emite desde el espejo A. Para el observador estacionario, parece que el pulso de luz tiene una trayectoria más larga para recorrer porque para cuando la luz llega al espejo B el reloj ya se ha movido algo en la dirección horizontal. Este es el mismo caso para el pulso de luz en su camino de regreso. El observador estacionario percibirá que tomará la luz un total de:

    imagen

    Geometría para un reloj en reposo: Esto ilustra el camino que la luz debe recorrer cuando el reloj está en reposo.

    \[\Delta t ^ { \prime } = \frac { 2 D } { c }\]

    para recorrer su camino. Podemos ver que D es más largo que L, así que eso significa que.

    imagen

    Geometría para un reloj en movimiento: Esto ilustra la trayectoria que la luz debe recorrer cuando el reloj se mueve desde la perspectiva de un observador estacionario.

    Ejemplo\(\PageIndex{2}\):

    Hemos establecido que en un marco de referencia que se mueve con relación al reloj (el observador estacionario se mueve en el marco de referencia del reloj), el reloj parece correr más lentamente. Ahora imaginemos que queremos medir la longitud de una regla. Esta vez imaginemos que te estás moviendo con velocidad v. Puedes determinar matemáticamente la longitud de la regla en tu marco de referencia (L ') multiplicando tu velocidad (v) por el tiempo que percibes que te lleva pasar por la regla (t'). Expresando esto en forma de ecuación, L '= vt'. Ahora bien, si alguien en el marco de descanso del gobernante quisiera determinar la longitud de la regla, podría hacer lo siguiente. Podrían determinar matemáticamente la longitud de la regla en su marco de referencia (L) multiplicando tu velocidad (v) por el tiempo que perciben que te lleva pasar por la regla (t). Esto se expresa en la siguiente ecuación: L = vt. Al igual que en la explicación del reloj, la regla parece estar moviéndose en su marco de referencia, por lo que t será más larga que t '(su intervalo de tiempo). En consecuencia, la longitud de la regla parecerá ser más corta en su marco de referencia (ocurrió el fenómeno de contracción de longitud).

    El efecto de la contracción de la longitud es insignificante a las velocidades diarias y puede ignorarse para todos los propósitos regulares. La contracción de la longitud se hace notable a una fracción sustancial de la velocidad de la luz (como se ilustra en) con la contracción solo en la dirección paralela a la dirección en la que viaja el cuerpo observado.

    imagen

    Longitud observada de un objeto: longitud observada de un objeto en reposo y a diferentes velocidades

    Ejemplo\(\PageIndex{3}\):

    Por ejemplo, a una velocidad de 13,400,000 m/s (30 millones de mph, .0447 c), la longitud es 99.9 por ciento de la longitud en reposo; a una velocidad de 42,300,000 m/s (95 millones de mph, 0.141 c), la longitud sigue siendo del 99 por ciento. A medida que la magnitud de la velocidad se acerca a la velocidad de la luz, el efecto se vuelve dominante. La fórmula matemática para la contracción de la longitud es:

    \[\mathrm { L } = \dfrac { \mathrm { L } _ { 0 } } { \gamma ( v ) } = \mathrm { L } _ { 0 } \sqrt { 1 - \dfrac { v ^ { 2 } } { \mathrm { c } ^ { 2 } } }\]

    donde L 0 es la longitud apropiada (la longitud del objeto en su cuadro de reposo); L es la longitud observada por un observador en movimiento relativo con respecto al objeto; v es la velocidad relativa entre el observador y el objeto en movimiento; c es la velocidad de la luz; y el factor Lorentz se define como:

    \[\gamma ( v ) = \dfrac { 1 } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }\]

    En esta ecuación se supone que el objeto es paralelo a su línea de movimiento. Para el observador en movimiento relativo, la longitud del objeto se mide restando las distancias medidas simultáneamente de ambos extremos del objeto. Un observador en reposo viendo un objeto viajando muy cerca de la velocidad de la luz observaría la longitud del objeto en la dirección del movimiento como muy cercana a cero.

    Puntos Clave

    • Según la teoría de la relatividad especial, es imposible decir en sentido absoluto si dos eventos distintos ocurren al mismo tiempo si esos eventos están separados en el espacio.
    • Una forma matemática de la relatividad de la simultaneidad fue introducida por Hendrik Lorentz e interpretada físicamente por Henri Poincaré. Las concepciones se basaron en el aether como marco de referencia preferido pero indetectable.
    • Albert Einstein dedujo el fracaso de la simultaneidad absoluta a partir de dos supuestos: 1) el principio de relatividad; 2) la constancia de la velocidad de la luz detectada en el espacio vacío, independiente del movimiento relativo de su fuente.
    • Los efectos de dilatación del tiempo son extremadamente pequeños para velocidades inferiores a 1/10 de la velocidad de la luz y pueden ignorarse con seguridad en la vida diaria.
    • Los efectos de dilatación del tiempo se vuelven importantes cuando un objeto se acerca a velocidades del orden de 30,000 km/s (1/10 la velocidad de la luz).
    • La fórmula para determinar la dilatación del tiempo es:\(\mathrm{\Delta t ^ { \prime } = \frac { \Delta t } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } }} }\).
    • A partir de una aplicación ingenua de la dilatación del tiempo, cada gemelo debe encontrar paradójicamente que el otro haya envejecido más lentamente.
    • El escenario se resuelve dentro del marco estándar de la relatividad especial: los gemelos no son equivalentes, el gemelo espacial experimenta una aceleración asimétrica adicional al cambiar de dirección para regresar a casa.
    • La paradoja gemela es útil como demostración de que la relatividad especial es autoconsistente.
    • La contracción de la longitud es insignificante a las velocidades diarias y puede ignorarse para todos los propósitos regulares.
    • La contracción de la longitud se hace notable a una fracción sustancial de la velocidad de la luz con la contracción solo en la dirección paralela a la dirección en la que viaja el cuerpo observado.
    • Un observador en reposo viendo un objeto viajando muy cerca de la velocidad de la luz observaría la longitud del objeto en la dirección del movimiento como muy cerca de cero.

    Términos Clave

    • aether: Sustancia o campo de relleno espacial, considerado necesario como medio de transmisión para la propagación de fuerzas electromagnéticas o gravitacionales.
    • relatividad especial: Una teoría que (descuidando los efectos de la gravedad) reconcilia el principio de relatividad con la observación de que la velocidad de la luz es constante en todos los marcos de referencia.
    • velocidad de la luz: la velocidad de la radiación electromagnética en un vacío perfecto: exactamente 299.792.458 metros por segundo por definición
    • dilatación del tiempo: La ralentización del paso del tiempo que experimentan los objetos en movimiento en relación con un observador; medible solo a velocidades relativistas.
    • Factor Lorentz: El factor, utilizado en la relatividad especial, para calcular el grado de dilatación temporal, contracción de longitud y masa relativista de un objeto que se mueve en relación con un observador.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    27.2: Consecuencias de la Relatividad Especial is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.