27.3: Cantidades relativistas

objetivos de aprendizaje

• Expresar fórmulas de adición de velocidad para objetos a velocidades mucho menores y acercándose a la velocidad de la luz

Una fórmula de adición de velocidad es una ecuación que relaciona las velocidades de objetos en movimiento en diferentes marcos de referencia.

Como observó Galileo Galilei en el siglo XVII, si un barco se mueve con relación a la costa a velocidad vv, y una mosca se mueve con la velocidad uu medida en el barco, calcular la velocidad de la mosca medida en la orilla es lo que se entiende por la adición de las velocidades vv y uu. Cuando tanto la mosca como la nave se mueven lentamente en comparación con la velocidad de la luz, es lo suficientemente precisa como para usar el vector sum s=u+vs=u+v donde ss es la velocidad de la mosca relativa a la orilla.

De acuerdo con la teoría de la relatividad especial, el marco de la nave tiene una frecuencia de reloj y medida de distancia diferentes, y se altera la noción de simultaneidad en la dirección del movimiento, por lo que se cambia la ley de adición para las velocidades.

Dado que la relatividad especial dicta que la velocidad de la luz es la misma en todos los marcos de referencia, la luz que brillaba desde la parte delantera de un automóvil en movimiento no puede ir más rápido que la luz de una lámpara estacionaria. Dado que esto va en contra de lo que Galileo solía agregar velocidades, es necesario que haya una nueva ley de adición de velocidad.

Este cambio no se nota a bajas velocidades pero a medida que la velocidad aumenta hacia la velocidad de la luz se vuelve importante. La ley de adición también se llama una ley de composición para las velocidades. Para los movimientos colineales, la velocidad de la mosca con respecto a la costa viene dada por la siguiente ecuación:

\[\mathrm { s } = \frac { \mathrm { v } + \mathrm { u } } { 1 + \mathrm { vu } / \mathrm { c } ^ { 2 } }\]

La ley de composición para las velocidades dio la primera prueba de la cinemática de la teoría especial de la relatividad. Utilizando un interferómetro Michelson, Hyppolite Fizeau midió la velocidad de la luz en un fluido que se movía paralelo a la luz en 1851. La velocidad de la luz en el fluido es más lenta que la velocidad de la luz en el vacío, y cambia si el fluido se mueve junto con la luz. La velocidad de la luz en un fluido colineal en movimiento se predice con precisión por el caso colineal de la fórmula relativista.

Configuración del experimento Fizeau: Un rayo de luz que emana de la fuente S' es reflejado por un divisor de haz G y es colimado en un haz paralelo por la lente L. Después de pasar las hendiduras O1 y O2, dos rayos de luz viajan a través de los tubos A1 y A2, a través de los cuales el agua está fluyendo de un lado a otro como mostrado por las flechas. Los rayos se reflejan en un espejo m en el foco de la lente L', de manera que un rayo siempre se propaga en la misma dirección que la corriente de agua, y el otro rayo opuesto a la dirección de la corriente de agua. Después de pasar de un lado a otro a través de los tubos, ambos rayos se unen en S, donde producen franjas de interferencia que se pueden visualizar a través del ocular ilustrado. El patrón de interferencia se puede analizar para determinar la velocidad de la luz que viaja a lo largo de cada pata del tubo.

Momentum relativista

El impulso relativista se da como\(\gamma \mathrm { m } _ { 0 } \mathrm { v }\) dónde\(\mathrm { m_0 }\) está la masa invariante del objeto y\(\gamma\) es la transformación de Lorentz.

objetivos de aprendizaje

• Compara Momentos newtonianos y relativistas para objetos a velocidades mucho menores y acercándose a la velocidad de la luz

Momentum relativista

La física newtoniana asume que el tiempo absoluto y el espacio existen fuera de cualquier observador. Esto da lugar a la relatividad galileana, que establece que las leyes del movimiento son las mismas en todos los marcos inerciales. También da como resultado una predicción de que la velocidad de la luz puede variar de un marco de referencia a otro. Sin embargo, esto es contrario a la observación. En la teoría de la relatividad especial, Albert Einstein mantiene el postulado de que las ecuaciones de movimiento no dependen del marco de referencia, sino que asume que la velocidad de la luz c es invariante. Como resultado, la posición y el tiempo en dos marcos de referencia se relacionan por la transformación de Lorentz en lugar de la transformación galileana.

Albert Einstein: Albert Einstein en 1921

Considere, por ejemplo, un marco de referencia que se mueve en relación con otro a velocidad v en la dirección x. La transformación galileana da las coordenadas del marco móvil como

\[\mathrm { t } ^ { \prime } = \mathrm { t }\]

\[\mathrm { x } ^ { \prime } = \mathrm { x } - \mathrm { v } \mathrm{ t } \]

mientras que la transformación de Lorentz da

\[\mathrm{t ^ { \prime } = \gamma \left( t - \dfrac { v x } { c ^ { 2 } } \right)}\]

\[\mathrm { x } ^ { \prime } = \gamma ( \mathrm { x } - \mathrm { v t} )\]

donde\(γ\) está el factor Lorentz:

\[\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } } }\]

Las leyes de conservación en física, como la ley de conservación del impulso, deben ser invariantes. Es decir, la propiedad que necesita ser conservada debe permanecer inalterada independientemente de los cambios en las condiciones de medición. Esto significa que la ley de conservación necesita sostenerse en cualquier marco de referencia. La segunda ley de Newton [con masa fijada en la expresión de impulso (p=m*v)], no es invariante bajo una transformación de Lorentz. Sin embargo, puede hacerse invariante haciendo que la masa inercial m de un objeto sea una función de la velocidad:

\[\mathrm { m } = \gamma \mathrm { m } _ { 0 }\]

donde\(\mathrm { m } _ { 0 }\) está la masa invariante del objeto.

El impulso modificado,

\[\mathrm { p } = \gamma \mathrm { m } _ { 0 } \mathrm { v }\]

obedece la segunda ley de Newton:

\[\mathrm { F } = \dfrac { \mathrm { d } \mathrm { p } } { \mathrm { d } t }\]

Es importante señalar que para velocidades mucho menores que la velocidad de la luz, el impulso newtoniano y el impulso relativista son aproximadamente los mismos. A medida que uno se acerca a la velocidad de la luz, sin embargo, el impulso relativista se vuelve infinito mientras que el impulso newtoniano continúa aumentando linealmente. Por lo tanto, es necesario emplear la expresión de impulso relativista cuando se trata de velocidades cercanas a la velocidad de la luz.

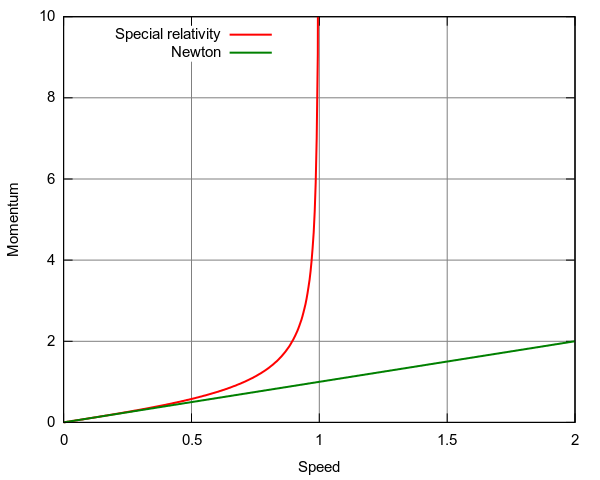
Momentum relativista y newtoniano: Esta figura ilustra que el impulso relativista se acerca al infinito a medida que se acerca la velocidad de la luz. El impulso newtoniano aumenta linealmente con la velocidad.

Energía Relativista y Masa

En la relatividad especial, a medida que el objeto se acerca a la velocidad de la luz, la energía y el impulso del objeto aumentan sin ataduras.

objetivos de aprendizaje

• Evaluar la posibilidad de que un objeto viaje a la velocidad de la luz

Energía Relativista y Masa

En la relatividad especial, un objeto que tiene una masa no puede viajar a la velocidad de la luz. A medida que el objeto se acerca a la velocidad de la luz, la energía y el impulso del objeto aumentan sin ataduras. Es necesario hacer correcciones relativistas de energía y masa debido a que la velocidad de la luz en el vacío es constante en todos los marcos de referencia. La conservación de la masa y la energía son leyes bien aceptadas de la física. Para que estas leyes se mantengan en todos los marcos de referencia, se debe aplicar la relatividad especial. Es importante señalar que para los objetos con velocidades que están muy por debajo de la velocidad de la luz, las expresiones para energía relativista y masa producen valores que son aproximadamente iguales a sus contrapartes newtonianas.

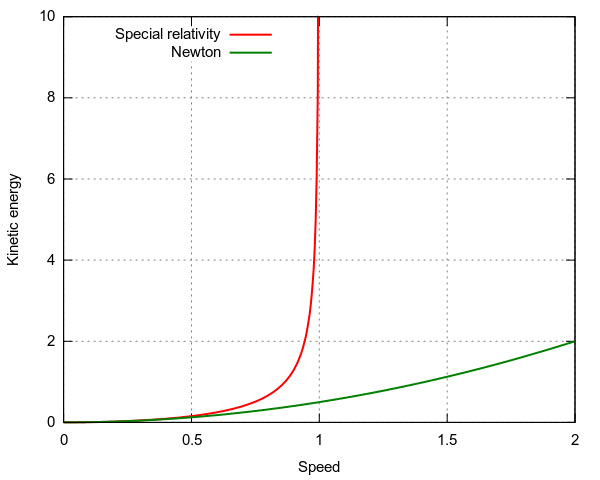
Energía cinética relativista y newtoniana: Esta figura ilustra cómo la energía cinética relativista y newtoniana se relacionan con la velocidad de un objeto. La energía cinética relativista aumenta hasta el infinito cuando un objeto se acerca a la velocidad de la luz, esto indica que ningún cuerpo con masa puede alcanzar la velocidad de la luz. Por otro lado, la energía cinética newtoniana sigue aumentando sin ataduras a medida que aumenta la velocidad de un objeto.

Misa relativista

La masa relativista fue definida por Richard C. Tolman fotografiado a la izquierda de Albert Einstein aquí en 1934 como la que sostiene para todas las partículas, incluidas las que se mueven a la velocidad de la luz. Para una partícula más lenta que la ligera, una partícula con una masa de reposo distinta de cero, la fórmula se convierte en donde está la masa de reposo y es el factor Lorentz. El factor Lorentz es igual a:\(\gamma = \frac { 1 } { \sqrt { 1 - \mathrm { v } ^ { 2 } / c ^ { 2 } } }\), donde v es la velocidad relativa entre los marcos de referencia inerciales y c es la velocidad de la luz.

Richard C. Tolman y Albert Einstein: Richard C. Tolman (1881 — 1948) con Albert Einstein (1879 — 1955) en Caltech, 1932

Cuando la velocidad relativa es cero, es simplemente igual a 1, y la masa relativista se reduce a la masa restante. A medida que la velocidad aumenta hacia la velocidad de la luz (c), el denominador del lado derecho se acerca a cero, y consecuentemente se acerca al infinito.

En la fórmula para el impulso la masa que ocurre es la masa relativista. En otras palabras, la masa relativista es la constante de proporcionalidad entre la velocidad y el momento.

Si bien la segunda ley de Newton sigue siendo válida en la forma la forma derivada no es válida porque en general no es una constante.

Energía Relativista

La energía relativista (\(\mathrm { E } _ { \mathrm { r } } = \sqrt { \left( \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } \right) ^ { 2 } + ( \mathrm { pc } ) ^ { 2 } }\)) se conecta con la masa de reposo a través de la siguiente ecuación:\(m = \frac { \sqrt { ( E ^ { 2 } - ( p c ) ^ { 2 } } } { c ^ { 2 } }\). Aquí el término representa el cuadrado de la norma euclidiana (longitud total del vector) de los diversos vectores de momento en el sistema, lo que reduce al cuadrado de la magnitud de impulso simple, si sólo se considera una sola partícula. Esta ecuación se reduce a cuando el término de impulso es cero. Para fotones donde la ecuación se reduce a.

Hoy en día, las predicciones de energía relativista y masa se confirman rutinariamente a partir de los datos experimentales de aceleradores de partículas como el Colisionador Relativista de Iones Pesados. El incremento del impulso relativista y la energía no sólo se mide con precisión sino que también es necesario para entender el comportamiento de los ciclotrones y sincrotrón, que aceleran las partículas hasta cerca de la velocidad de la luz.

Materia y Antimateria

La antimateria está compuesta por antipartículas, que tienen la misma masa que las partículas de materia ordinaria pero carga opuesta y espín cuántico.

objetivos de aprendizaje

• Describir las propiedades de las antipartículas

La antimateria es un material compuesto por antipartículas, que tienen la misma masa que las partículas de materia ordinaria pero tienen carga opuesta y espín cuántico. Las antipartículas se unen entre sí para formar antimateria de la misma manera que las partículas normales se unen para formar materia normal. Por ejemplo, un positrón (la antipartícula del electrón, con símbolo e ⁺) y un antiprotón (símbolo p ^—) pueden formar un átomo antihidrógeno. Además, mezclar materia y antimateria puede conducir a la aniquilación de ambas, de la misma manera que la mezcla de antipartículas y partículas lo hace. Esto da lugar a fotones de alta energía (rayos gamma) y otros pares de partículas-antipartículas. El resultado final de la materia de encuentro de antimateria es una liberación de energía proporcional a la masa, como se muestra en la ecuación de equivalencia masa-energía, E = mc ².

Antihidrógeno y Átomos de Hidrógeno: El antihidrógeno consiste en un antiprotón y un positrón; el hidrógeno consiste en un protón y un electrón.

Casi toda la materia observable desde la tierra parece estar hecha de materia más que de antimateria. Si existieran regiones del espacio dominadas por antimateria, los rayos gamma producidos en las reacciones de aniquilación a lo largo del límite entre la materia y las regiones de antimateria serían detectables.

La antimateria aún puede existir en cantidades relativamente grandes en galaxias lejanas debido a la inflación cósmica en la época primordial del universo. Se espera que las galaxias de antimateria, si existen, tengan la misma química y espectros de absorción y emisión que las galaxias de materia normal, y sus objetos astronómicos serían observacionalmente idénticos, dificultando su distinción de las galaxias de materia normal.

Se especula considerable sobre por qué el universo observable aparentemente está compuesto casi en su totalidad de materia (a diferencia de una mezcla de materia y antimateria), si existen otros lugares que están compuestos casi en su totalidad de antimateria en su lugar, y qué tipo de tecnología podría ser posible si la antimateria podría ser aprovechada. En este momento, la aparente asimetría de materia y antimateria en el universo visible es uno de los mayores problemas sin resolver de la física.

Energía cinética relativista

La energía cinética relativista se puede expresar como:\(\mathrm { E } _ { \mathrm { k } } = \frac { \mathrm { mc } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } ) } } - \mathrm { mc } ^ { 2 }\) donde mm es masa de reposo,\(\mathrm{v}\) es velocidad,\(\mathrm{c}\) es velocidad de la luz.

objetivos de aprendizaje

• Comparar energías cinéticas clásicas y relativistas para objetos a velocidades mucho menores y acercándose a la velocidad de la luz

En la mecánica clásica, la energía cinética de un objeto depende de la masa de un cuerpo así como de su velocidad. La energía cinética es igual a la masa multiplicada por el cuadrado de la velocidad, multiplicada por la constante 1/2. La ecuación se da como:

\[\mathrm { E } _ { \mathrm { k } } = \dfrac { 1 } { 2 } \mathrm { m } \mathrm { v } ^ { 2 }\]

donde mm es la masa y vv es la velocidad (o la velocidad) del cuerpo.

La energía cinética clásica de un objeto se relaciona con su impulso por la ecuación:

\[\mathrm { E } _ { \mathrm { k } } = \dfrac { \mathrm { p } ^ { 2 } } { 2 \mathrm { m } }\]

donde pp es momentum.

Si la velocidad de un cuerpo es una fracción significativa de la velocidad de la luz, es necesario emplear una relatividad especial para calcular su energía cinética. Es importante saber cómo aplicar relatividad especial a problemas con partículas de alta velocidad. En la relatividad especial, debemos cambiar la expresión de impulso lineal. Usando mm para la masa de reposo,\(\mathrm{v}\) y\(\mathcal { V }\) para la velocidad y velocidad del objeto respectivamente, y cc para la velocidad de la luz en vacío, la expresión relativista para el momento lineal es:

Revista Time — 1 de julio de 1946: La conexión popular entre Einstein,\(\mathrm{E = mc^2}\), y la bomba atómica fue señalada de manera destacada en la portada de la revista Time (julio de 1946) por la escritura de la ecuación sobre la propia nube de hongos.

\(\mathrm { p } = \mathrm { m } \gamma \mathrm { v }\), donde\(γ\) está el factor Lorentz:

\(\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm{ v } / \mathrm { c } ) ^ { 2 } } }\)

Dado que la energía cinética de un objeto está relacionada con su impulso, sabemos intuitivamente que la expresión relativista de la energía cinética también será diferente de su contraparte clásica. En efecto, la expresión relativista de la energía cinética es:

\[\mathrm { E } _ { \mathrm { k } } = \dfrac { \mathrm { mc } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } ) } } - \mathrm { mc } ^ { 2 }\]

La ecuación muestra que la energía de un objeto se acerca al infinito a medida que la velocidad vv se acerca a la velocidad de la luz cc. Por lo tanto, es imposible acelerar un objeto a través de esta frontera.

El subproducto matemático de este cálculo es la fórmula de equivalencia masa-energía (a la que se hace referencia en). El cuerpo en reposo debe tener un contenido energético igual a:

\[\mathrm { E } _ { \mathrm { rest } } = \mathrm { E } _ { 0 } = \mathrm { mc } ^ { 2 }\]

La expresión general de la energía cinética de un objeto que no está en reposo es:

\(\mathrm { KE } = \mathrm { mc } ^ { 2 } - \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 }\), donde m es la masa relativista del objeto y m ₀ es la masa restante del objeto.

A baja velocidad (v<<cv<<c), la energía cinética relativista puede aproximarse bien por la energía cinética clásica. Podemos demostrar que esto es cierto usando una expansión de Taylor para la raíz cuadrada recíproca y manteniendo los dos primeros términos de la ecuación relativista de energía cinética. Cuando hacemos esto obtenemos:

\[\mathrm { E } _ { \mathrm { k } } \approx \mathrm { mc } ^ { 2 } \left( 1 + \frac { 1 } { 2 } \mathrm { v } ^ { 2 } / \mathrm { c } ^ { 2 } \right) - \mathrm { mc } ^ { 2 } = \dfrac { 1 } { 2 } \mathrm { mv } ^ { 2 }\]

Así, la energía total se puede dividir en la energía de la masa de reposo más la energía cinética clásica tradicional a bajas velocidades.

Puntos Clave

• Cuando dos objetos se mueven lentamente en comparación con la velocidad de la luz, es lo suficientemente preciso como para usar la suma vectorial de velocidades:\(\mathrm{s=u+v}\).
• A medida que la velocidad aumenta hacia la velocidad de la luz, la suma vectorial de velocidades se reemplaza por:\(\mathrm { s } = \frac { \mathrm { v } + \mathrm { u } } { 1 + \mathrm { vu } / \mathrm { c } ^ { 2 } }\).
• La ley de composición para las velocidades dio la primera prueba de la cinemática de la teoría especial de la relatividad cuando, utilizando un interferómetro Michelson, Hyppolite Fizeau midió la velocidad de la luz en un fluido que se mueve paralelo a la luz.
• La física newtoniana asume que el tiempo absoluto y el espacio existen fuera de cualquier observador, lo que resulta en una predicción de que la velocidad de la luz puede variar de un marco de referencia a otro.
• En la teoría de la relatividad especial, las ecuaciones de movimiento no dependen del marco de referencia mientras que la velocidad de la luz (c) es invariante.
• Dentro del dominio de la mecánica clásica, el impulso relativista se aproxima estrechamente al impulso newtoniano. A baja velocidad γm0vγm0v es aproximadamente igual a m0vm0v, la expresión newtoniana para el momento.
• En la relatividad especial, un objeto que tiene una masa no puede viajar a la velocidad de la luz.
• La masa relativista se define como\(\mathrm { m } _ { \mathrm { rel } } = \frac { \mathrm { E } } { \mathrm { c } ^ { 2 } }\) y puede verse como la constante de proporcionalidad entre la velocidad y el momento.
• La energía relativista se conecta con la masa de reposo a través de la siguiente ecuación:\(\mathrm { E } _ { \mathrm { r } } = \sqrt { \left( \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } \right) ^ { 2 } + ( \mathrm { pc } ) ^ { 2 } }\).
• El resultado final de la materia de encuentro de antimateria es una liberación de energía proporcional a la masa, como se muestra en la ecuación de equivalencia masa-energía,\(\mathrm{E = mc^2}\).
• Aunque casi toda la materia observable desde la Tierra parece estar hecha de materia en lugar de antimateria, la antimateria todavía puede existir en cantidades relativamente grandes en galaxias lejanas.
• No existe explicación alguna para la aparente asimetría de materia y antimateria en el universo visible.
• La ecuación relativista de energía cinética muestra que la energía de un objeto se acerca al infinito a medida que la velocidad se acerca a la velocidad de la luz. Por lo tanto, es imposible acelerar un objeto a través de esta frontera.
• Los cálculos de energía cinética conducen a la fórmula de equivalencia masa-energía:\(\mathrm { E } _ { \mathrm { rest } } = \mathrm { E } _ { 0 } = \mathrm { mc } ^ { 2 }\).
• A baja velocidad (\(\mathrm { v } < < \mathrm { C }\)), la energía cinética relativista puede ser aproximada por la energía cinética clásica. Así, la energía total se puede dividir en la energía de la masa de reposo más la energía cinética newtoniana tradicional a bajas velocidades.

Términos Clave

• relatividad especial: Una teoría que (descuidando los efectos de la gravedad) reconcilia el principio de relatividad con la observación de que la velocidad de la luz es constante en todos los marcos de referencia.
• interferómetro: Cualquiera de varios instrumentos que utilizan la interferencia de las ondas para determinar longitudes de onda y velocidades de onda, determinar índices de refracción y medir pequeñas distancias, cambios de temperatura, tensiones y muchas otras mediciones útiles.
• velocidad de la luz: la velocidad de la radiación electromagnética en un vacío perfecto: exactamente 299.792.458 metros por segundo por definición
• Transformación galileana: una transformación utilizada para transformar entre las coordenadas de dos marcos de referencia que difieren solo por el movimiento relativo constante dentro de los constructos de la física newtoniana.
• Transformación de Lorentz: una transformación que relaciona las coordenadas espacio-tiempo de un marco de referencia con otro en relatividad especial
• Factor Lorentz: El factor, utilizado en la relatividad especial, para calcular el grado de dilatación temporal, contracción de longitud y masa relativista de un objeto que se mueve en relación con un observador.
• masa de reposo: la masa de un cuerpo cuando no se mueve en relación con un observador
• aniquilación: el proceso de una partícula y su correspondiente antipartícula combinándose para producir energía
• positrón: El equivalente de antimateria de un electrón, que tiene la misma masa pero una carga positiva.
• antimateria: materia que se compone de las antipartículas de las que constituyen materia normal
• mecánica clásica: Todas las leyes físicas de la naturaleza que dan cuenta del comportamiento del mundo normal, pero que se descomponen al tratar con lo muy pequeño (ver mecánica cuántica) o lo muy rápido o muy pesado (ver relatividad).

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• Fórmula de adición de velocidad. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/velocidad-adición_fórmula. Licencia: CC BY-SA: Atribución-CompartirIgual
• Fórmula de adición de velocidad. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/velocidad-adición_fórmula. Licencia: CC BY-SA: Atribución-CompartirIgual
• interferómetro. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/interferómetro. Licencia: CC BY-SA: Atribución-CompartirIgual
• relatividad especial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/special_relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• velocidad de la luz. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/speed_of_light. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/thumb/a/a7/Fizeau-Mascart1_retouched.png/799px-Fizeau-Mascart1_retouched.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Invariante (física). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Invariant_ (física). Licencia: CC BY-SA: Atribución-CompartirIgual
• Momentum. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Momentum. Licencia: CC BY-SA: Atribución-CompartirIgual
• Cuatro ímpetu. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Four-Momentum. Licencia: CC BY-SA: Atribución-CompartirIgual
• Transformación galileana. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Galilean%20Transformación. Licencia: CC BY-SA: Atribución-CompartirIgual
• Transformación de Lorentz. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/Lorentz_Transformation. Licencia: CC BY-SA: Atribución-CompartirIgual
• relatividad especial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/special_relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/thumb/a/a7/Fizeau-Mascart1_retouched.png/799px-Fizeau-Mascart1_retouched.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/f/f5/Einstein_1921_Portrait2.jpg/480px-einstein_1921_Portrait2.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Misa en relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Mass_en_especial_relativity%23Relativistic_Mass. Licencia: CC BY-SA: Atribución-CompartirIgual
• relatividad especial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/special_relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Misa. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Masa%23Masa_y_Energy_en_Especial_Relatividad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Pruebas de relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Special_Relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Misa en relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Mass_en_Special_Relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Equivalencia masa-energía. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Masa-Energy_Equivalencia. Licencia: CC BY-SA: Atribución-CompartirIgual
• Misa en relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Mass_en_especial_relativity%23Relativistic_Mass. Licencia: CC BY-SA: Atribución-CompartirIgual
• masa de descanso. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/rest_mass. Licencia: CC BY-SA: Atribución-CompartirIgual
• Factor Lorentz. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/Lorentz_Factor. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/thumb/a/a7/Fizeau-Mascart1_retouched.png/799px-Fizeau-Mascart1_retouched.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/f/f5/Einstein_1921_Portrait2.jpg/480px-einstein_1921_Portrait2.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/c/c7/Tolman_&_Einstein.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Antimateria. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Antimatter. Licencia: CC BY-SA: Atribución-CompartirIgual
• Tomografía por emisión de positrones. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Positron_Emission_Tomography. Licencia: CC BY-SA: Atribución-CompartirIgual
• antimateria. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/antimateria. Licencia: CC BY-SA: Atribución-CompartirIgual
• aniquilación. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/aniquilación. Licencia: CC BY-SA: Atribución-CompartirIgual
• positrón. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/positron. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/thumb/a/a7/Fizeau-Mascart1_retouched.png/799px-Fizeau-Mascart1_retouched.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/f/f5/Einstein_1921_Portrait2.jpg/480px-einstein_1921_Portrait2.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/c/c7/Tolman_&_Einstein.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/b/b8/3d_image_of_antihidrogeno.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• relatividad especial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/special_relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Energía cinética. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Kinetic_Energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• Principio de correspondencia. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Correspondence_principle. Licencia: CC BY-SA: Atribución-CompartirIgual
• Energía cinética. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Kinetic_Energy. Licencia: CC BY-SA: Atribución-CompartirIgual
• mecánica clásica. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/classical_mecanics. Licencia: CC BY-SA: Atribución-CompartirIgual
• Factor Lorentz. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/Lorentz_Factor. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/thumb/a/a7/Fizeau-Mascart1_retouched.png/799px-Fizeau-Mascart1_retouched.png. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/thumb/f/f5/Einstein_1921_Portrait2.jpg/480px-einstein_1921_Portrait2.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Pruebas de energía relativista e impulso. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tests_of_Relativistic_Energy_Y_Momentum. Licencia: CC BY: Atribución
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/c/c7/Tolman_&_Einstein.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/commons/b/b8/3d_image_of_antihidrogeno.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual
• Proporcionado por: Wikimedia. Ubicado en: Upload.wikimedia.org/wikipedia/es/5/57/Einstein_-_time_magazine_-_july_1, _1946.jpg. Licencia: CC BY-SA: Atribución-CompartirIgual