27.4: Implicaciones de la Relatividad Especial

objetivos de aprendizaje

• Formular cambios importantes en la comprensión del tiempo, el espacio, la masa y la energía que fueron introducidos por la teoría de la Relatividad Especial

La teoría de la Relatividad Especial y sus implicaciones impulsaron un cambio de paradigma en nuestra comprensión de la naturaleza del universo, cuyo tejido fundamental es el espacio y el tiempo. Antes de 1905, los científicos consideraban el espacio y el tiempo como objetos completamente independientes. El tiempo no podía afectar el espacio y el espacio no podía afectar el tiempo. Después de 1905, sin embargo, la Teoría Especial de la Relatividad destruyó esta visión vieja pero intuitiva. Específicamente, la Relatividad Especial nos mostró que el espacio y el tiempo no son independientes entre sí sino que pueden mezclarse entre sí y por lo tanto deben considerarse como el mismo objeto, al que denotaremos como espacio-tiempo. Las consecuencias de la mezcla espacio/tiempo son:

• dilatación del tiempo
• y contracción de longitud.

Otras consecuencias importantes que se discutirán en otra sección son:

• Relatividad de Simultaneidad (para ciertos eventos, la secuencia en la que ocurren depende del observador)
• Nada puede moverse más rápido que la velocidad de la luz (denotaremos el valor de la velocidad de la luz como cc)

¿Por qué hay una mezcla entre el espacio y el tiempo? Para examinar esto debemos conocer los principios fundacionales de la relatividad. Ellos son:

1. El principio de relatividad: Las leyes de la física para los observadores que no se aceleran entre sí deberían ser las mismas.
2. El principio de la velocidad de la luz invariante: Todos los observadores, moviéndose a velocidad constante, miden la misma velocidad de la luz independientemente de lo rápido que se muevan.

Si uno acepta el segundo principio como hecho entonces inmediatamente sigue que el espacio y el tiempo no son independientes. ¿Por qué? Veamos el experimento en el que hay una fuente de luz, un observador fijo y un cohete que se mueve hacia la fuente de luz. Los dos observadores están relacionados por una transformación coordenada, o espacio-tiempo. El segundo principio nos dice entonces que no importa cuán rápido se mueva el cohete, ambos observadores deben medir la misma velocidad de la luz que emana de la fuente. La única forma en que esto puede suceder es si el reloj del observador de cohetes está marcando a un ritmo diferente al del observador estacionario. ¿Qué tan diferente? Esto se puede expresar en la ecuación de dilatación temporal:

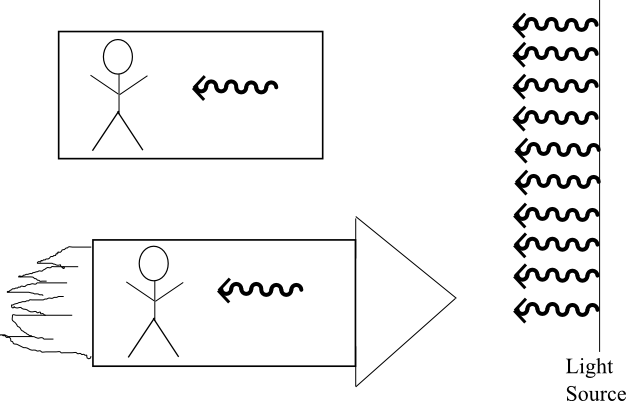
Medición de la luz: Un observador estacionario medirá la misma velocidad de la luz que un observador que se mueve en un cohete incluso si ese cohete se está moviendo cerca de la velocidad de la luz.

\[\mathrm { t } _ { \mathrm { s } } = \dfrac { \mathrm { t } _ { \mathrm { m } } } { \sqrt { 1 - \left( \dfrac { \mathrm{v} ^ { 2 } } { \mathrm { c } ^ { 2 } } \right) } }\]

Donde tsts es el tiempo transcurrido para el observador estacionario, tmtm es el tiempo transcurrido para el observador en movimiento, y vv es la velocidad del cohete medida desde el marco estacionario. Entonces se puede ver que como\(\mathrm { V } \rightarrow \mathrm { C }\) entonces el tiempo transcurrido en el marco estacionario va al infinito. Para colocar algunos números, dejar\(\mathrm { v } = 0.99986 \mathrm { c }\), y\(\mathrm { t } _ { \mathrm { m } } = \mathrm { 1 \; sec } \). El tiempo transcurrido en el marco estacionario es entonces de una hora. Así por cada segundo vivido en el cohete, ¡el hombre estacionario vive una hora!

Uno de los resultados más radicales de la dilatación del tiempo es la llamada “paradoja de los gemelos”. La paradoja de los gemelos es un experimento mental en relatividad especial que involucra a gemelos idénticos. Uno de los gemelos emprende un viaje al espacio en un cohete que tiene una velocidad cercana a la velocidad de la luz. Al regresar a casa el gemelo encuentra que el gemelo que permaneció en la Tierra ha envejecido más. Esta consecuencia alteró la percepción de que el envejecimiento es necesariamente constante.

El factor raíz cuadrada en la ecuación de dilatación temporal es muy importante y lo denotamos como:

Este factor aparece frecuentemente en la relatividad especial. Por ejemplo, la fórmula de contracción de longitud es:

\[\mathrm { L } = \mathrm { L } _ { 0 } \sqrt { 1 - \left( \dfrac { \mathrm{v} } { \mathrm{c} } \right) } = \dfrac { \mathrm { L } _ { 0 } } { \gamma }\]

donde\(\mathrm{L_0}\) es la longitud de reposo, la longitud de un objeto medida en el marco de movimiento conjunto del objeto, y\(\mathrm{L}\) es la longitud del objeto medida por el observador que ve el objeto moviéndose a velocidad\(\mathrm{v}\). En nuestro ejemplo de cohete, el observador estacionario mide la longitud del cohete como menor de lo que mediría alguien que se estaba moviendo con el cohete. Esto alteró la percepción de que la longitud de un objeto aparecería igual independientemente del marco de referencia del observador.

Otro hallazgo radical que fue posible gracias al descubrimiento de la relatividad especial es la equivalencia de energía y masa. Combinados con otras leyes de la física, los postulados de la relatividad especial predicen que la masa y la energía están relacionadas por:\(\mathrm{E=mc^2}\), donde c es la velocidad de la luz en el vacío. Esto alteró la percepción de que la masa y la energía son cosas completamente diferentes y allanó el camino para la energía nuclear y las armas nucleares.

Como nota final es importante señalar cuán grande es la velocidad de la luz comparada con la vida cotidiana. La velocidad de la luz es:

\[\mathrm { c } = 3 \times 10 ^ { 8 } \mathrm { m } / \mathrm { s }\]

Así, en la vida cotidiana\(\mathrm{γ≈1}\) y no experimentamos dilatación significativa en el tiempo o contracción de la longitud. Si lo hiciéramos, la vida sería muy diferente.

Espacio-tiempo de cuatro dimensiones

Vivimos en el espacio-tiempo de cuatro dimensiones, en el que el orden de ciertos eventos puede depender del observador.

objetivos de aprendizaje

• Formular los principales resultados de la relatividad especial

Trabajo en cuatro dimensiones

Examinemos a dos observadores que se mueven uno con relación al otro a una velocidad constante. Los denotaremos como observador A y observador A'. El observador A establece un sistema de coordenadas espacio-tiempo (t, x, y, z); de manera similar, A' establece su propio sistema de coordenadas espacio-tiempo (t', x', y', z'). (Véase un ejemplo) Por lo tanto, ambos observadores viven en un mundo de cuatro dimensiones con tres dimensiones espaciales y una dimensión temporal.

Dos sistemas de coordenadas: Dos sistemas de coordenadas en los que el marco cebado se mueve con velocidad v con respecto al marco no cebado

No debería resultarle extraño trabajar con cuatro dimensiones; cada vez que tenga que encontrarse con su amigo en algún lugar hay que decirle cuatro variables: dónde (tres coordenadas espaciales) y cuándo (una coordenada de tiempo). Es decir, siempre hemos vivido en cuatro dimensiones, pero hasta ahora probablemente hayas pensado en el espacio y el tiempo como completamente separados.

El movimiento de la luz en cuatro dimensiones

Volvamos a nuestro ejemplo: supongamos que en algún momento del espacio-tiempo hay un haz de luz que emerge. Ambos observadores miden hasta qué punto ha recorrido la viga en cada punto del tiempo y cuánto tiempo tardó en viajar para recorrer esa distancia. Es decir, el observador A mide:

\(\mathrm{( \Delta t , \Delta x , \Delta y , \Delta z )}\)

donde, por ejemplo,\(\mathrm{\Delta t = t - t _ { 0 }}\); t es el momento en que tuvo lugar la medición; y t ₀ es el momento en que se encendió la luz.

De igual manera, el observador A' mide:

\(\left( \Delta t ^ { \prime } , \Delta x ^ { \prime } , \Delta y ^ { \prime } , \Delta z ^ { \prime } \right)\)

donde establecemos el sistema de tal manera que ambos observadores estén de acuerdo\(\left( \mathrm { t } _ { 0 } , \mathrm { x } _ { 0 } , \mathrm { y } _ { 0 } , \mathrm { z } _ { 0 } \right)\). Debido a la invarianza de la velocidad de la luz ambos observadores acordarán:

\[\dfrac { \Delta \mathrm { X } ^ { 2 } + \Delta \mathrm { Y } ^ { 2 } + \Delta \mathrm { Z } ^ { 2 } } { \Delta \mathrm { T } ^ { 2 } } = \mathrm { c } ^ { 2 } \rightarrow 0 = - \mathrm { c } ^ { 2 } \Delta \mathrm { T } ^ { 2 } + \Delta \mathrm { X } ^ { 2 } + \Delta \mathrm { Y } ^ { 2 } + \Delta \mathrm { Z } ^ { 2 }\]

donde\(\mathrm{(T,X,Y,Z)}\) se refiere a las coordenadas en cualquiera de los fotogramas. Por lo tanto, existe una regla específica que todos los caminos de luz deben seguir. Para eventos generales podemos definir la cantidad:

\[\mathrm{s} ^ { 2 } = - \mathrm{c} ^ { 2 } \Delta t ^ { 2 } + \Delta \mathrm{x} ^ { 2 } + \Delta \mathrm{y} ^ { 2 } + \Delta \mathrm{z} ^ { 2 }\]

Esto se conoce como el elemento de línea y es el mismo para todos los observadores. (Usando los principios de la relatividad, puedes probar esto para separaciones generales, no solo rayos de luz). El conjunto de todas las transformaciones de coordenadas que dejan invariante la cantidad anterior se conoce como Transformaciones de Lorentz. De ello se deduce que los sistemas de coordenadas de todos los observadores físicos están relacionados entre sí por Lorentz Transformaciones. (El conjunto de todas las transformaciones de Lorentz forman lo que los matemáticos llaman un grupo, y el estudio de la teoría de grupos ha revolucionado la física). Para la transformación de coordenadas en, las transformaciones son:

\[\left. \begin{array} { l } { \mathrm { t } ^ { \prime } = \gamma \left( \mathrm { t } - \mathrm { vx } / \mathrm { c } ^ { 2 } \right) } \\ { \mathrm { x } ^ { \prime } = \gamma ( \mathrm { x } - \mathrm { vt } ) } \\ { \mathrm { y } ^ { \prime } = \mathrm { y } } \\ { \mathrm { z } ^ { \prime } = \mathrm { z } } \end{array} \right.\]

donde

\[\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm{ v } / \mathrm { c } ) ^ { 2 } } }\]

Definimos la separación entre puntos espacio-tiempo de la siguiente manera:

\[\mathrm { s } ^ { 2 } > 0 : \text { space-like }\]

\[\mathrm { s } ^ { 2 } < 0 : \text { time-like }\]

\[\mathrm { s } ^ { 2 } = 0 : \text { null }\]

Separamos estos eventos porque son muy diferentes. Por ejemplo, para una separación espacial siempre se puede encontrar una transformación de coordenadas que revierta el orden de tiempo de los eventos (intente probarlo para el ejemplo en). Este fenómeno se conoce como la relatividad de la simultaneidad y puede ser contradictorio.

Separaciones Espacio-Tiempo

Examinemos dos choques automovilísticos, uno en Nueva York y otro en Londres, de tal manera que ocurren al mismo tiempo en un solo marco. En esta situación, la separación espacio-tiempo entre los dos eventos es similar al espacio. La cuestión de si los eventos son simultáneos es relativa: en algunos marcos de referencia los dos accidentes pueden ocurrir al mismo tiempo; en otros marcos (en un estado de movimiento diferente en relación con los eventos) el accidente en Londres puede ocurrir primero; y en otros fotogramas más el accidente de Nueva York puede ocurrir primero. (En la práctica, esto no nos afecta porque los fotogramas que cambian el orden de los eventos deben moverse a velocidades inalcanzables).

Separaciones espacio-tiempo nulas y espacio-tiempo nulas

Los eventos que son similares al tiempo o nulos no comparten esta propiedad y, por lo tanto, existe un ordenamiento causal entre eventos similares al tiempo. En otras palabras, si dos eventos están separados como en el tiempo, entonces pueden afectarse entre sí. La razón es que si dos puntos espacio-tiempo son similares al tiempo o separados nulos, uno siempre puede enviar una señal luminosa de un punto a otro.

Relatividad Especial

Finalmente, discutamos un resultado importante de la relatividad especial: que la energía EE de un objeto que se mueve con velocidad vv es:

\[\mathrm { E } = \frac { \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } } } = \mathrm { mc } ^ { 2 }\]

donde m0m0 es la masa del objeto en reposo y m=γm0m=γm0 es la masa cuando el objeto se mueve. La fórmula anterior muestra inmediatamente por qué es imposible viajar más rápido que la velocidad de la luz. As\(\mathrm { v } \rightarrow \mathrm { c } , \mathrm { m } \rightarrow \infty \), y se necesita una cantidad infinita de energía para acelerar aún más el objeto.

El universo relativista

La gravedad es un efecto geométrico en el que una matriz métrica juega un papel especial, y el movimiento de los objetos se ve alterado por el espacio curvo.

objetivos de aprendizaje

• Identificar factores que afectan el movimiento cerca de objetos masivos

Relatividad

La relatividad especial indica que los humanos viven en un espacio-tiempo de cuatro dimensiones donde la 'distancia' ssbetween puntos en el espacio-tiempo puede considerarse como:

\ [\ mathrm {s} ^ {2} = -\ mathrm {c} ^ {2}\ Delta\ mathrm {t} ^ {2} +\ Delta\ mathrm {x} ^ {2} +\ Delta\ mathrm {y} ^ {2} +\ Delta\ mathrm {z} ^ {2} =\ mathrm {X} ^ {\ mathrm {T}} eta\ mathrm {X}

La última ecuación es una relación matricial en la que TT denota transposición (para vectores\(\mathrm { A } ^ { \mathrm { T } } \mathrm { B } = \mathrm { A } \cdot \mathrm { B }\)),\(\mathrm{X}\) es el vector\) (\ mathrm {c}\ Delta\ mathrm {t},\ Delta\ mathrm {x},\ Delta\ mathrm {y},\ Delta\ mathrm {z})\), y\(\mathrm{η}\) es la matriz:

\[\eta = \left( \begin{array} { c c c c } { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 1 } \end{array} \right)\]

Una matriz que va entre dos vectores para dar una longitud se llama métrica. En matemáticas, una función métrica o distancia es una función que define una distancia entre elementos de un conjunto. En este caso, el conjunto es el espacio-tiempo y los elementos son puntos en ese espacio-tiempo. Un espacio-tiempo con la métrica ηη se llama espacio Minkowski y ηη es la métrica Minkowski.

El espacio-tiempo de Minkowski de cuatro dimensiones es solo uno de los muchos espacio-tiempos diferentes posibles (geometrías) que difieren en su matriz métrica. Una matriz métrica arbitraria se puede denotar como gg, lo que plantea preguntas sobre lo que representan los espacio-tiempos con diferentes métricas. En 1916, Einstein encontró la importancia de estos espacio-tiempos en su teoría de la relatividad general.

Relatividad General

La relatividad general, o la teoría general de la relatividad, es la teoría geométrica de la gravitación publicada por Albert Einstein en 1916. Es la descripción actual de la gravitación en la física moderna. La relatividad general generaliza la relatividad especial y la ley de Newton de la gravitación universal, proporcionando una descripción unificada de la gravedad como propiedad geométrica del espacio y el tiempo, o espacio-tiempo. En particular, la curvatura del espacio-tiempo está directamente relacionada con la energía y el impulso de cualquier materia y radiación que estén presentes. La relación es especificada por las ecuaciones de campo de Einstein, un sistema de ecuaciones diferenciales parciales.

\[\text { g } \leftrightarrow \text { curvature } \leftrightarrow \text { Energy and Momentum }\]

Las personas pueden usar la métrica para calcular la curvatura y luego usar las ecuaciones de campo de Einstein para relacionar la curvatura con la energía y el impulso del espacio-tiempo. Yendo en el orden inverso, la energía y el impulso afectan la curvatura y el espacio-tiempo. Así, la energía y el momento curvan espacio-tiempo. El espacio Minkowski es el espacio especial desprovisto de materia, y como resultado, es completamente plano. La definición precisa de curvatura requiere conocimientos de matemáticas avanzadas, pero una manera intuitiva de entenderla es que la definición de una línea recta cambia en el espacio-tiempo curvo.

Un ejemplo pictórico se muestra en la siguiente figura, donde cualquier cosa que esté cerca de la Tierra tiene su movimiento alterado debido al espacio-tiempo curvo. Esta alteración del movimiento afecta a los satélites, la luna, e incluso a los humanos. Si el espacio alrededor de la Tierra fuera plano, los humanos simplemente flotarían si saltaran hacia arriba. Dado que la Tierra altera el espacio-tiempo, los humanos son arrastrados hacia la Tierra. En esencia, la gravedad es un efecto geométrico.

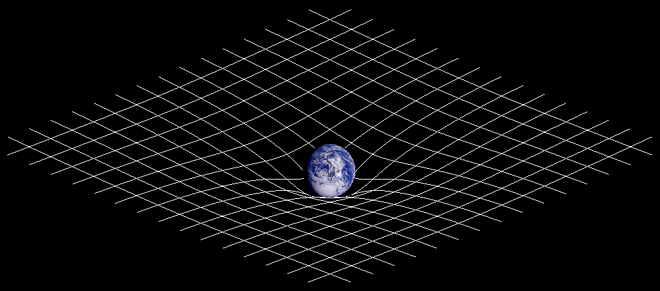
Curvatura del espacio-tiempo: La Tierra masiva está alterando la curvatura del espacio-tiempo.

Puntos Clave

• El tiempo es relativo.
• Las longitudes de los objetos en movimiento son diferentes que si sus longitudes se midieran en un marco de movimiento conjunto.
• El tiempo y el espacio no son independientes.
• Vivimos en un universo de cuatro dimensiones; las tres primeras dimensiones son espaciales, y la cuarta es el tiempo.
• El sistema de coordenadas de observadores físicos se relaciona entre sí a través de transformaciones de Lorentz.
• Nada puede viajar más rápido que la velocidad de la luz.
• La matriz métrica se puede utilizar para calcular la curvatura del espacio-tiempo.
• La curvatura puede relacionarse con la energía y el impulso a través de las ecuaciones de Einstein.
• Debido a la curvatura del espacio-tiempo, el movimiento de los objetos se altera cerca de objetos masivos.

Términos Clave

• relatividad especial: Una teoría que (descuidando los efectos de la gravedad) reconcilia el principio de relatividad con la observación de que la velocidad de la luz es constante en todos los marcos de referencia.
• dilatación del tiempo: La ralentización del paso del tiempo que experimentan los objetos en movimiento en relación con un observador; medible solo a velocidades relativistas.
• contracción de longitud: Los observadores miden la longitud de un objeto en movimiento como menor de lo que sería si estuviera estacionario.
• elemento de línea: Una cantidad invariante en relatividad especial
• Transformación de Lorentz: una transformación que relaciona las coordenadas espacio-tiempo de un marco de referencia con otro en relatividad especial
• relatividad de la simultaneidad: Para puntos espacio-temporales separados similares al espacio, el orden de tiempo entre eventos es relativo.
• relatividad general: Una teoría que extiende la relatividad especial y da cuenta uniformemente de la gravedad y los marcos de referencia acelerados, postulando que el espacio-tiempo se curva en presencia de masa.
• Espacio Minkowski: Un espacio-tiempo plano de cuatro dimensiones. Porque es plano, está desprovisto de materia.
• metric: Una función métrica, o distancia, es una función que define una distancia entre elementos de un conjunto.

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• relatividad especial. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/special_relativity. Licencia: CC BY-SA: Atribución-CompartirIgual
• Relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Especial_Relatividad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Velocidad de sonido. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Speed_of_Sound. Licencia: CC BY-SA: Atribución-CompartirIgual
• Dilatación del tiempo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Tiempo_Dilation%23Muon_Lifetime. Licencia: CC BY-SA: Atribución-CompartirIgual
• contracción de longitud. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Length%20Contraction. Licencia: CC BY-SA: Atribución-CompartirIgual
• dilatación del tiempo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/time_dilation. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Amazon Web Services. Ubicado en: s3.amazonaws.com/figures.boundless.com/50947657e4b0b4558d8e4fac/sr_lightmeasure. png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Relatividad especial. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Especial_Relatividad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Relatividad de simultaneidad. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/relatividad_de_simultaneidad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/products/line-element. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/definición/relatividad-de-simultaneidad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Transformación de Lorentz. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/Lorentz_Transformation. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Amazon Web Services. Ubicado en: s3.amazonaws.com/figures.boundless.com/50947657e4b0b4558d8e4fac/sr_lightmeasure. png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Archivo:Marcos de referencia en relativo motion.svg - Wikipedia, la enciclopedia libre. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/w/index. php*title=file:frames_of_reference_in_relative_motion.svg&page=1. Licencia: CC BY-SA: Atribución-CompartirIgual
• Relatividad general. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/General_Relatividad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Métrica (matemáticas). Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Metric_ (matemáticas). Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//physics/minkowski-space—2. Licencia: CC BY-SA: Atribución-CompartirIgual
• métrico. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Metric. Licencia: CC BY-SA: Atribución-CompartirIgual
• relatividad general. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/general_relatividad. Licencia: CC BY-SA: Atribución-CompartirIgual
• Sin límites. Proporcionado por: Amazon Web Services. Ubicado en: s3.amazonaws.com/figures.boundless.com/50947657e4b0b4558d8e4fac/sr_lightmeasure. png. Licencia: Dominio Público: No Conocido Derechos de Autor
• Archivo:Marcos de referencia en relativo motion.svg - Wikipedia, la enciclopedia libre. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/w/index. php*title=file:frames_of_reference_in_relative_motion.svg&page=1. Licencia: CC BY-SA: Atribución-CompartirIgual
• Curvatura espacio-tiempo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Archivo:SpaceTime_Curvature.png. Licencia: CC BY-SA: Atribución-CompartirIgual