4.2: Fuerza y Masa

Última actualización
Guardar como PDF

Page ID: 127952

Boundless
Boundless

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Fuerza

La fuerza es cualquier influencia que hace que un objeto cambie, ya sea con respecto a su movimiento, dirección o construcción geométrica.

objetivos de aprendizaje

Desarrollar la relación entre masa y aceleración en la determinación de la fuerza

Descripción general de las fuerzas

En física, una fuerza es cualquier influencia que provoca que un objeto sufra un cierto cambio, ya sea en lo que respecta a su movimiento, dirección o construcción geométrica. Se mide con la unidad SI de Newtons. Una fuerza es aquella que puede hacer que un objeto con masa cambie su velocidad, es decir, que se acelere, o que pueda hacer que un objeto flexible se deforme. La fuerza también se puede describir mediante conceptos intuitivos como empujar o tirar. Una fuerza tiene tanto magnitud como dirección, convirtiéndola en una cantidad vectorial.

¿Qué es una fuerza? : Describe qué son las fuerzas y qué hacen.

Cualidades de la Fuerza

La forma original de la segunda ley de Newton establece que la fuerza neta que actúa sobre un objeto es igual a la velocidad a la que cambia su impulso. Esta ley se da además para significar que la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre el objeto, está en la dirección de la fuerza neta, y es inversamente proporcional a la masa del objeto.

Como mencionamos, la fuerza es una cantidad vectorial. Un vector es una matriz unidimensional con elementos tanto de magnitud como de dirección. En un vector de fuerza, la masa\(\mathrm{m}\), es la componente de magnitud y la aceleración,\(\mathrm{a}\), es la componente direccional. La ecuación para la fuerza está escrita:

\[\mathrm{F=m⋅a}\]

Los conceptos relacionados con la fuerza incluyen empuje, que aumenta la velocidad de un objeto; arrastre, que disminuye la velocidad de un objeto; y par que produce cambios en la velocidad de rotación de un objeto. Las fuerzas que no actúan uniformemente sobre todas las partes de un cuerpo también causarán tensiones mecánicas, término técnico para influencias que causan deformación de la materia. Si bien la tensión mecánica puede permanecer incrustada en un objeto sólido, deformándolo gradualmente, la tensión mecánica en un fluido determina los cambios en su presión y volumen.

Dinámica

La dinámica es el estudio de las fuerzas que hacen que los objetos y sistemas se muevan. Para entender esto, necesitamos una definición de trabajo de fuerza. Nuestra definición intuitiva de fuerza, es decir, un empuje o un tirón, es un buen lugar para comenzar. Sabemos que un push o pull tiene tanto magnitud como dirección (por lo tanto, es una cantidad vectorial) y puede variar considerablemente en cada aspecto.

muestra algunos ejemplos de la naturaleza “push-pull” de la fuerza. El ejemplo superior izquierdo es el de un sistema de poleas. La fuerza que alguien tendría que tirar hacia abajo sobre el cable tendría que igualar y superar la fuerza que hace la masa el objeto y los efectos de la gravedad sobre esos objetos para que el sistema se mueva hacia arriba. El ejemplo superior derecho muestra que cualquier objeto que descanse sobre una superficie seguirá ejerciendo fuerza sobre esa superficie. El ejemplo inferior es el de dos imanes que son atraídos entre sí debido a la fuerza magnética.

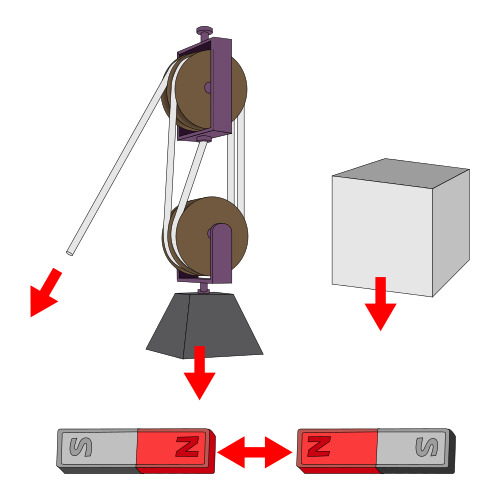
imagen

Ejemplos de Fuerza: Algunas situaciones en las que las fuerzas están en juego.

Masa

La masa es una propiedad física de la materia que depende del tamaño y forma de la materia, y es expresada en kilogramos por el sistema SI.

objetivos de aprendizaje

Justificar la importancia de comprender la masa en la física

¿Qué es la misa?

Todos los elementos tienen propiedades físicas cuyos valores pueden ayudar a describir un estado físico de los elementos. Los cambios en estas propiedades pueden describir transformaciones elementales. Las propiedades físicas no cambian la naturaleza química de la materia. La propiedad física que estamos cubriendo en este átomo se llama masa.

La masa se define como una medida cuantitativa de la resistencia de un objeto a la aceleración. Los términos masa y peso a menudo se intercambian, sin embargo es incorrecto hacerlo. El peso es una propiedad diferente de la materia que, si bien está relacionada con la masa, no es la masa, sino la cantidad de fuerza gravitacional que actúa sobre un determinado cuerpo de materia. La masa es una propiedad intrínseca que nunca cambia.

Unidades de Masa

Para medir algo, se debe establecer un valor estándar para utilizarlo en relación con el objeto de medición. A esta relación se le llama unidad. El Sistema Internacional de Unidades (SI) mide la masa en kilogramos, o kg. Existen otras unidades de masa, entre ellas las siguientes (solo las dos primeras son aceptadas por el sistema SI):

t — Tonelada; 1t = 1000kg
u — unidad de masa atómica; 1u ~= 1.66×10 ^-27 kg
sl — babosa
lb — libra

Conceptos Usando Masa

Peso — ver
Newtons Segunda Ley — la masa tiene un papel central en la determinación del comportamiento de los cuerpos. Newtons Segunda Ley relaciona la fuerza f, ejercida en un cuerpo de masa m, con la aceleración del cuerpo a:\(\mathrm{F=ma}\)
Momento-masa relaciona el impulso de un cuerpo, p, con su velocidad lineal, v:\(\mathrm{p = mv}\)
Energía cinética: la masa relaciona la energía cinética, K con la velocidad, v:\(\mathrm{K=\frac{1}{2}m|v^2|}\)

Puntos Clave

La fuerza se establece como una cantidad vectorial, es decir, tiene elementos tanto de magnitud como de dirección. Masa y aceleración respectivamente.
En términos laicos, la fuerza es un empuje o un tirón que se puede definir en términos de diversos estándares.
La dinámica es el estudio de la fuerza que provoca que objetos y sistemas se muevan o deformen.
Las fuerzas externas son todas las fuerzas externas que actúan sobre un cuerpo, y las fuerzas internas son cualquier fuerza que actúa dentro de un cuerpo.
La masa se define como una medida cuantitativa de la resistencia de un objeto a la aceleración.
Según la segunda ley de movimiento de Newton, si un cuerpo de masa fija m es sometido a una sola fuerza F, su aceleración a viene dada por F/m.
La masa es central en muchos conceptos de la física, incluyendo:peso, impulso, aceleración y energía cinética.
Según la segunda ley de movimiento de Newton, si un cuerpo de masa fija m es sometido a una sola fuerza F, su aceleración a viene dada por F/m.

Términos Clave

fuerza: Una fuerza es cualquier influencia que provoca que un objeto sufra un cierto cambio, ya sea en lo que respecta a su movimiento, dirección o construcción geométrica.
velocidad: Una cantidad vectorial que denota la velocidad de cambio de posición con respecto al tiempo, o una velocidad con una componente direccional.
vector: Una cantidad dirigida, una con magnitud y dirección; la entre dos puntos.
masa: La cantidad de materia que contiene un cuerpo, independientemente de su volumen o volumen. Es una de las cuatro propiedades fundamentales de la materia. Se mide en kilogramos en el sistema de medición SI.

Search

Text Color

Text Size

Margin Size

Font Type