Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.4: Teorema de trabajo-energía

Última actualización

30 oct 2022
Guardar como PDF
- 6.3: Trabajo realizado por una Fuerza Variable
- 6.5: Energía Potencial y Conservación de la Energía

Boundless
Boundless

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Teorema de Energía Cinética y Energía de Trabajo

El teorema trabajo-energía establece que el trabajo realizado por todas las fuerzas que actúan sobre una partícula equivale al cambio en la energía cinética de la partícula.

objetivos de aprendizaje

Esbozar la derivación del teorema trabajo-energía

El teorema de la energía del trabajo

El principio de trabajo y energía cinética (también conocido como teorema trabajo-energía) establece que el trabajo realizado por la suma de todas las fuerzas que actúan sobre una partícula equivale al cambio en la energía cinética de la partícula. Esta definición se puede extender a cuerpos rígidos definiendo el trabajo del par y la energía cinética rotacional.

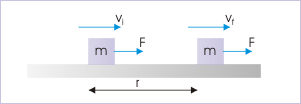
imagen

Energía cinética: Una fuerza sí funciona en el bloque. La energía cinética del bloque aumenta como resultado por la cantidad de trabajo. Esta relación se generaliza en el teorema trabajo-energía.

El trabajo W realizado por la fuerza neta sobre una partícula equivale al cambio en la energía cinética de la partícula K E:

$\mathrm{W=ΔKE=\dfrac{1}{2}mv_f^2−\dfrac{1}{2}mv_i^2}$

donde v _i y v _f son las velocidades de la partícula antes y después de la aplicación de la fuerza, y m es la masa de la partícula.

Derivación

En aras de la simplicidad, consideraremos el caso en el que la fuerza resultante F es constante tanto en magnitud como en dirección y es paralela a la velocidad de la partícula. La partícula se mueve con aceleración constante a a lo largo de una línea recta. La relación entre la fuerza neta y la aceleración viene dada por la ecuación F = ma (segunda ley de Newton), y el desplazamiento de la partícula d, se puede determinar a partir de la ecuación:

$\mathrm{v_f^2=v_i^2+2ad}$

obtener,

$\mathrm{d=\dfrac{v^2_f−v^2_i}{2a}}$

El trabajo de la fuerza neta se calcula como el producto de su magnitud (F=mA) y el desplazamiento de la partícula. Sustituyendo las ecuaciones anteriores rinde:

$\mathrm{W=Fd=ma\dfrac{v^2_f−v^2_i}{2a}=\dfrac{1}{2}mv^2_f−\dfrac{1}{2}mv^2_i=KE_f−KE_i=ΔKE}$

Puntos Clave

El trabajo W realizado por la fuerza neta sobre una partícula equivale al cambio en la energía cinética de la partícula K E: $\mathrm{W=ΔKE=\frac{1}{2}mv_f^2−\frac{1}{2}mv_i^2}$ .
El teorema trabajo-energía puede derivarse de la segunda ley de Newton.
El trabajo transfiere energía de un lugar a otro o de una forma a otra. En sistemas más generales que el sistema de partículas aquí mencionado, el trabajo puede cambiar la energía potencial de un dispositivo mecánico, la energía térmica en un sistema térmico, o la energía eléctrica en un dispositivo eléctrico.

Términos Clave

par: Un efecto de rotación o torsión de una fuerza; (unidad SI newton-metro o Nm; unidad imperial pie-libra o ft-lb)

Teorema de Energía Cinética y Energía de Trabajo

El teorema de la energía del trabajo

Derivación

Puntos Clave

Términos Clave

Support Center

How can we help?