3.2: Movimiento con Aceleración Constante

Hasta ahora, hemos considerado el movimiento donde la velocidad es una constante (es decir, donde la velocidad no cambia con el tiempo). Supongamos que deseamos describir la posición de un objeto que cae que liberamos del descanso en el tiempo\(t=0\text{s}\). El objeto comenzará con una velocidad de 0 m/s y se acelerará a medida que cae. Decimos que un objeto está “acelerando” si su velocidad no es constante. Como veremos en capítulos posteriores, los objetos que caen cerca de la superficie de la Tierra experimentan una aceleración constante (su velocidad cambia a un ritmo constante).

Formalmente, definimos la aceleración como la velocidad de cambio de velocidad. Recordemos que la velocidad es la velocidad de cambio de posición, por lo que la aceleración es a la velocidad lo que es la velocidad a la posición. En particular, vimos que si la velocidad,\(v_{x}\), es constante, entonces la posición en función del tiempo viene dada por:

\[x(t) = x_{0} + v_{x}t\]

En analogía, si la aceleración es constante, entonces la velocidad en función del tiempo viene dada por:

\[v_{x}(t) = v_{0x} + a_{x}t\]

donde\(a_{x}\) está la “aceleración” y\(v_{0x}\) es la velocidad del objeto a\(t=0\). Podemos elaborar las dimensiones de aceleración para que esta ecuación tenga sentido. Ya que estamos sumando\(v_{0x}\) y\(a_{x}t\), necesitamos que las dimensiones\(a_{x}t\) de ser velocidad:

\(\begin{aligned} \left[a_{x}t\right]&=\frac{L}{T} \\ \left[a_{x}\right]&=\frac{L}{T^{2}} \end{aligned}\)

Por lo tanto, la aceleración tiene dimensiones de longitud a lo largo del tiempo al cuadrado, con las correspondientes unidades S.I. de\(\text{m/s}^{2}\) (metros por segundo al cuadrado o metros por segundo por segundo). Para describir la posición de un objeto que se está acelerando, no podemos usar la Ecuación 3.2.1, ya que sólo es correcta si la velocidad es constante.

En la Sección 3.3 Usando cálculo para obtener aceleración desde la posición, mostraremos que la posición en función del tiempo,\(x(t)\), de un objeto con aceleración constante,\(a_{x}\), viene dada por:

\[x(t)=x_{0}+v_{0x}t+\frac{1}{2}a_{x}t^{2}\]

donde, a\(t = 0\), el objeto estaba en posición\(x = x_{0}\) y tenía una velocidad\(v_{0x}\).

Ejemplo\(\PageIndex{1}\)

Se lanza una pelota hacia arriba con una velocidad de\(10\text{m/s}\). ¿Después de qué distancia se detendrá la pelota antes de volver a caer? Supongamos que la gravedad provoca una aceleración descendente constante de\(9.8\text{m/s}^{2}\).

Solución:

Resolveremos este problema en los siguientes pasos:

1. Configurar un sistema de coordenadas (definir el\(x\) eje).
2. Identificar la condición que corresponde a que la pelota detenga su movimiento hacia arriba y caiga de nuevo hacia abajo.
3. Determinar la distancia a la que se detuvo la pelota.

Ya que lanzamos la pelota hacia arriba con una velocidad inicial hacia arriba, tiene sentido elegir un\(x\) -eje que apunte hacia arriba y tenga el origen en el punto donde soltamos la pelota. Con esta elección, haciendo referencia a las variables de la Ecuación 3.2.3, tenemos:

\(\begin{aligned} x_{0}&=0 \\ v_{0x}&=+10\text{m/s} \\ a_{x}&=-9.8\text{m/s}^{2} \end{aligned}\)

donde la velocidad inicial está en la dirección x positiva, y la aceleración,\(a_{x}\), está en la dirección negativa (la velocidad será cada vez más pequeña, por lo que su tasa de cambio es negativa).

La condición para que la pelota se detenga en la parte superior de la trayectoria es que su velocidad sea cero (eso es lo que significa detenerse). Podemos usar la Ecuación 3.2.2 para encontrar a qué hora corresponde:

\(\begin{aligned} v(t)&=v_{0x}+a_{x}t \\ 0&=(10\text{m/s})+(-9.8\text{m/s}^{2})t \\ \therefore t&=\frac{(10\text{m/s})}{(9.8\text{m/s}^{2})}=1.02\text{s} \end{aligned}\)

Ahora que sabemos que tardó en llegar\(1.02\text{s}\) a lo más alto de la trayectoria, podemos encontrar cuánta distancia se recorrió:

\(\begin{aligned} x(t)&=x_{0}+v_{0x}t+\frac{1}{2}a_{x}t^{2} \\ x&=(0\text{m})+(10\text{m/s})(1.02\text{s})+\frac{1}{2}(-9.8\text{m/s}^{2})(1.02\text{s})^{2}=5.10\text{m} \end{aligned}\)

y encontramos que la pelota se levantará\(5.10\text{m}\) antes de volver a caer.

Visualización del movimiento con aceleración constante

Cuando un objeto tiene una aceleración constante, su velocidad y posición en función del tiempo se describen mediante las dos ecuaciones siguientes:

\(\begin{aligned} v(t)&=v_{0x}+a_{x}t \\ x(t)&=x_{0}+v_{0x}t + \frac{1}{2}a_{x}t^{2} \end{aligned}\)

donde la velocidad cambia linealmente con el tiempo, y la posición cambia cuadráticamente con el tiempo (va como\(t^{2}\)). La figura\(\PageIndex{1}\) muestra la posición y la velocidad en función del tiempo para el balón del Ejemplo 3.2.1 para los tres primeros segundos del movimiento.

Figura\(\PageIndex{1}\): Posición y velocidad en función del tiempo para la pelota en el Ejemplo 3.2.1.

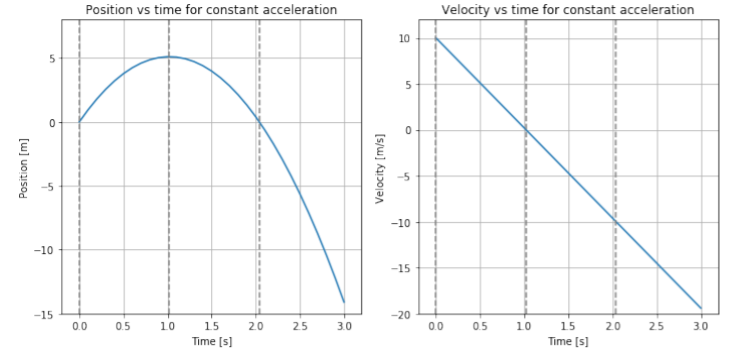
Podemos dividir el movimiento en tres partes (mostradas por las líneas discontinuas verticales en la Figura\(\PageIndex{1}\)):

1) Entre\(t=0\text{s}\) y\(t=1.02\text{s}\)

En el momento\(t=0\text{s}\), la pelota comienza en una posición de\(x=0\text{m}\) (panel izquierdo) y tiene una velocidad de\(v_{0x}=10\text{m/s}\) (panel derecho). Durante el primer segundo de movimiento, la posición,\((t)\), aumenta (la pelota se mueve hacia arriba), hasta que la posición deja de aumentar en\(t=1.02\text{s}\), como se encuentra en el Ejemplo 3.2.1. Durante ese tiempo, la velocidad disminuye linealmente de\(10\text{m/s}\) a\(0\text{m/s}\) debido a la constante aceleración negativa de la gravedad. A\(t=1.02\text{s}\), la velocidad es instantánea\(0\text{m/s}\) y la pelota está momentáneamente en reposo (ya que alcanza la parte superior de la trayectoria antes de volver a caer).

2) Entre\(t=1.02\text{s}\) y\(t=2.04\text{s}\)

A\(t=1.02\text{s}\), la velocidad continúa disminuyendo linealmente (se vuelve cada vez más negativa) a medida que la pelota comienza a caer de nuevo cada vez más rápido. La posición también comienza a disminuir justo después\(t=1.02\text{s}\), ya que la pelota vuelve a bajar al punto de liberación. At\(t=2.04\text{s}\), la pelota regresa al punto desde el que fue lanzada, y la pelota va con la\((10\text{m/s})\) misma velocidad que cuando fue liberada, pero la velocidad es negativa (movimiento hacia abajo).

3) Después\(t=2.04\text{s}\)

Si no hay nada que detenga la pelota, ésta continúa moviéndose hacia abajo con una velocidad cada vez mayor. La posición sigue volviéndose más negativa y la velocidad sigue siendo mayor en magnitud y más negativa.

Ejercicio\(\PageIndex{1}\)

Realizar un boceto de la aceleración en función del tiempo correspondiente a la posición y velocidad que se muestran en la Figura\(\PageIndex{1}\).

Contestar

Velocidad versus velocidad

En el ejemplo anterior, nuestro lenguaje no era tan preciso como debería ser a la hora de dirigir la ciencia. Específicamente, necesitamos una manera de distinguir la situación cuando la velocidad está disminuyendo (volviéndose más negativa), mientras que el objeto en realidad va cada vez más rápido (después\(t=1.02\text{s}\)). Utilizaremos el término velocidad para referirnos a qué tan rápido se mueve un objeto (cuánta distancia cubre por unidad de tiempo), y usaremos el término velocidad para indicar también la dirección del movimiento. En otras palabras, la velocidad es el valor absoluto de la velocidad. La velocidad es así siempre positiva, mientras que la velocidad también puede ser negativa.

Con este vocabulario, la velocidad de la pelota disminuye entre\(t=0\text{s}\) y\(t=1.02\text{s}\), y aumenta a partir de entonces. Por otro lado, la velocidad disminuye continuamente (siempre es cada vez más negativa). Velocidad es así el término más general ya que nos dice tanto la velocidad como la dirección del movimiento.