7.6: Problemas y soluciones de la muestra
- Page ID
- 129456
Ejercicio\(\PageIndex{1}\)
Una lata de salto de esquí se modela como una rampa de altura\(h=5\text{m}\), como se muestra en la Figura\(\PageIndex{1}\). El área de aterrizaje se encuentra a la misma altura que la parte inferior de la rampa. Un esquiador de masa\(m=80\text{kg}\) se mueve a una velocidad\(v_i=15\text{m/s}\) cuando llega al fondo de la rampa. Cuando el esquiador aterriza el salto, su velocidad se mide para ser\(v_f=12\text{m/s}\). Ignorar resistencia al aire.
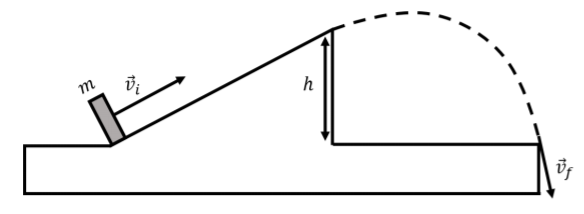
- ¿Cuál es la velocidad del esquiador en el instante en que dejan el salto de esquí, en la parte superior de la rampa?
- Usa la respuesta de la parte (a) para encontrar el trabajo realizado por fricción la fricción entre la rampa y el esquiador.
- Contestar
-
Comenzamos definiendo un sistema de coordenadas. Elegimos el\(x\) eje para que sea horizontal y positivo en la dirección del movimiento, y elegimos el\(y\) eje para que sea vertical y la dirección positiva hacia arriba.
Determinaremos la velocidad en la parte superior de la rampa\(v_t\), utilizando el Teorema de Trabajo-Energía:
\ begin {alinear*} W^ {net} =\ frac {1} {2} mv_f^2-\ frac {1} {2} mv_t^2\ end {align*}
donde\(W^{net}\) esta el trabajo de red realizado en el esquiador mientras “vuela” por el aire. Mientras el esquiador está en el aire, la única fuerza que actúa sobre ellos es la gravedad,\(\vec F=-mg\hat y\). El camino del esquiador es una parábola, de manera que el vector de desplazamiento cambia de dirección continuamente.
El trabajo realizado por gravedad viene dado por:
\ begin {align*} W =\ int\ vec f_g\ cdot d\ vec l\ end {alinear*}
donde\(d\vec l\) es un desplazamiento infinitesimal a lo largo de la trayectoria, como se muestra en la Figura\(\PageIndex{2}\).
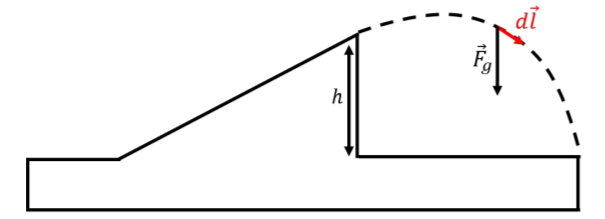
Figura\(\PageIndex{2}\): Desplazamiento infinitesimal a lo largo de la trayectoria del salto. El vector de desplazamiento tendrá\(x\) y\(y\) componentes:
\ start {alinear*} d\ vec l = dx\ hat x + dy\ hat y\ end {alinear*}
El producto escalar con la fuerza de la gravedad es así:
\ begin {alinear*}\ vec f_g\ cdot d\ vec l &= (-mg\ hat y)\ cdot (dx\ hat x + dy\ hat y) = -mgdy\ end {align*}
El trabajo realizado por gravedad puede convertirse así en una integral over\(y\) (para la cual conocemos los valores de inicio y final), y viene dado por:
\ begin {alinear*} W =\ int\ vec f_g\ cdot d\ vec l =\ int_h^0 -mgdy = [-mgy] _h^0 = mgh\ end {alinear*}
El trabajo realizado por gravedad es positivo, lo cual tiene sentido, ya que la fuerza de gravedad generalmente se encuentra en la misma dirección que el desplazamiento neto (hacia abajo). No fue necesario tomar en cuenta la forma específica de la trayectoria, porque la fuerza fue constante en magnitud y dirección (ver Ejemplo 7.1.4).
Ahora podemos encontrar la velocidad del esquiador cuando abandona el salto usando el teorema de Trabajo-Energía:
\ begin {align*} W^ {net} &=\ frac {1} {2} mv_f^2-\ frac {1} {2} mv_t^2\\ mgh &=\ frac {1} {2} mv_f^2-\ frac {1} {2} mv_t^2\\\ por lo tanto v_t&=\ sqrt {v_f^2-2gh} =\ sqrt {(12\ texto {m/s}) ^2 - 2 (9.8\ texto {m/s} ^ {2}) (5\ texto {m})} =6.8\ texto {m/s}\ end {alinear*}
b. podemos utilizar de nuevo el Teorema de Trabajo-Energía para determinar el trabajo realizado por fricción a medida que el esquiador se desliza por la rampa. Sabemos que la velocidad del esquiador en la parte inferior de la rampa es\(v_i\), y acabamos de encontrar que la velocidad del esquiador en la parte superior de la rampa es\(v_t=\sqrt{v_f^2-2gh}\). El trabajo neto realizado en el esquiador que sube por la rampa es igual a:
\ begin {align*} W^ {net} &=\ frac {1} {2} mv_t^2-\ frac {1} {2} mv_i^2\\ &=\ frac {1} {2} m (v_t^2-v_i^2) =\ frac {1} {2} m (v_f^2-2gh -v_i^2)\\ &=\ frac {1} {2} m (v_f^2-v_i^2) -mgh\ end {alinear*}
El trabajo neto realizado es también la suma del trabajo realizado por cada una de las fuerzas que actúan sobre el esquiador a medida que se deslizan por la rampa. Las fuerzas sobre el esquiador son la fuerza de gravedad, la fuerza de fricción y la fuerza normal. La fuerza normal no funciona, ya que siempre es perpendicular al desplazamiento. El trabajo neto es así la suma del trabajo realizado por la fuerza gravedad\(W_g\), y el trabajo realizado por la fuerza de fricción\(W_f\), sobre el desplazamiento correspondiente a la longitud de la rampa:
\ begin {align*} W^ {net} =w_g+w_f\ end {align*}
El trabajo realizado por gravedad es:
\ begin {alinear*} w_g =\ vec f_g\ cdot\ vec d = (-mg\ hat y)\ cdot (d_x\ hat x + h\ hat y) = -mgh\ end {alinear*}
donde\(\vec d\) está el vector de desplazamiento hacia arriba de la rampa (distancia horizontal desconocida\(d_x\), y distancia vertical,\(h\)). Ahora podemos determinar el trabajo realizado por la fuerza de fricción:
\ begin {align*} W^ {net} &=W_g+W_F\\\ frac {1} {2} m (v_f^2-v_i^2) -mgh &= -mgh + w_f\\ por lo tanto w_f &=\ frac {1} {2} m (v_f^2-v_i^2) =\ frac {1} {2} (80\ texto {kg}) ((12\ texto {m/s}) ^2- (15\ texto {m/s}) ^2) =-3240\ texto {J}\ final {alinear*}
Y encontramos que la fuerza de fricción hizo trabajo negativo (redujo la energía cinética del esquiador).
Discusión:
A lo largo del salto, el esquiador arrancó en la parte inferior de la rampa con una energía cinética dada, luego perdió parte de esa energía subiendo por la rampa (en forma de pérdida por fricción y trabajo negativo realizado por gravedad). Durante la fase aerotransportada, la gravedad hizo un trabajo positivo y el esquiador recuperó parte de la energía cinética que habían perdido subiendo por la rampa. Así, el trabajo neto realizado por la fuerza de fricción es la diferencia de energías cinéticas entre el punto de aterrizaje final y el inicio de la rampa, ya que la fricción es la única fuerza que realizó una cantidad neta de trabajo (negativo) a lo largo de toda la trayectoria (la gravedad no hizo trabajo neto en toda la trayectoria). Este ejemplo muestra cómo podemos empezar a pensar en la energía como algo que se “conserva”, lo que exploraremos con más detalle en el próximo capítulo.
Ejercicio\(\PageIndex{2}\)
Un niño de masa\(m\) se sienta en un columpio de longitud\(L\), como en la Figura\(\PageIndex{3}\). Empujas al niño con una fuerza horizontal\(\vec F\). Se aplica la fuerza de tal manera que el niño se mueve a una velocidad constante (nota que no\(\vec F\) tendrá una magnitud constante).}
- ¿Cuánto trabajo haces para mover al niño de\(\theta=0\) a\(\theta=\theta_1\)?
- Utilice un diagrama detallado para mostrar que el trabajo realizado por\(\vec F\) es igual a\(mgh\), donde\(h\) está el cambio de altura del niño.
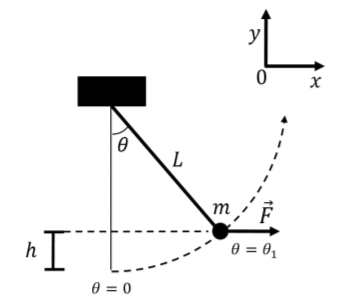
- Contestar
-
a. queremos encontrar el trabajo realizado por la fuerza aplicada\(\vec F\). Primero necesitamos encontrar una expresión para la magnitud de\(\vec F\), con base en el hecho de que el niño no está acelerando. Las fuerzas sobre el niño son:
- \(\vec F_g\), su peso, con magnitud\(mg\).
- \(\vec F_T\), la tensión en la cuerda, que cambia con el ángulo,\(\theta\).
- \(\vec F\), la fuerza aplicada, que cambia de magnitud a medida que cambia el ángulo\(\theta\),,.
Las fuerzas se ilustran en la Figura\(\PageIndex{4}\).
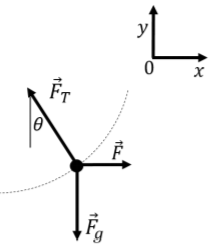
Figura\(\PageIndex{4}\): Diagrama de cuerpo libre de las fuerzas ejercidas sobre el niño. El niño se mueve a una velocidad constante, por lo que la fuerza neta es igual a cero. La suma de las\(x\) y\(y\) componentes de las fuerzas es igual a cero (Segunda Ley de Newton):
\ begin {align*}\ suma F_x &= F-F_T\ sin\ theta =0\\\ suma F_y &= F_T\ cos\ theta -mg = 0\ end {align*}
La reordenación de estas ecuaciones da:
\ begin {align*} F&=F_T\ sin\ theta\\ mg&=F_T\ cos\ theta\ end {align*}
Queremos una expresión para\(F\) que no dependa de\(F_T\) (ya que\(F_T\) se desconoce), así podemos dividir una ecuación entre la otra:
\ begin {alinear*}\ frac {F} {mg} &=\ frac {F_T\ sin\ theta} {F_T\ cos\ theta} =\ tan\ theta\\ por lo tanto F (\ theta) &=mg\ tan\ theta\ end {alinear*}
donde indicamos que la fuerza\(\vec F(\theta)\) depende del ángulo\(\theta\). El trabajo realizado por la fuerza,\(\vec F\), viene dado por:
\ begin {align*} W_F=\ int_a^b\ vec F (\ theta)\ cdot d\ vec l\ end {align*}
\(d\vec l\)es el “elemento path” a lo largo de parte del arco de círculo sobre el que se mueve el niño, como se ilustra en la Figura\(\PageIndex{5}\). Tenemos una expresión de cómo\(\vec F\) cambia de magnitud en función del ángulo\(\theta\), y así sería conveniente realizar la integral sobre el ángulo\(\theta\).
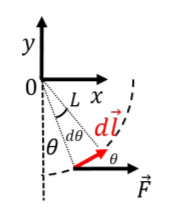
Figura\(\PageIndex{5}\): Un elemento de trayectoria a lo largo de la trayectoria circular del columpio. Podemos usar coordenadas polares,\((r,\theta)\), en lugar de coordenadas cartesianas para describir el vector de desplazamiento,\(d\vec l\). Si el vector subtiende un arco en el círculo que forma un ángulo infinitesimal\(d\theta\), como se ilustra, entonces la longitud del vector\(d\vec l\) viene dada por:
\ comenzar {alinear*} dl = L d\ theta\ final {alinear*}
donde\(L\) está el radio del círculo. El vector\(d\vec l\) hace un ángulo\(\theta\) con la horizontal, y por lo tanto con el vector,\(\vec F\). El producto punto entre\(\vec F\) y, por lo tanto, se\(d\vec l\) puede escribir como:
\ start {alinear*}\ vec F (\ theta)\ cdot d\ vec l = Fdl\ cos\ theta= (mg\ tan\ theta) (Ld\ theta)\ cos\ theta=mgl\ sin\ theta d\ theta\ end {align*}
Ahora podemos escribir la integral para la obra usando límite que se basan en el ángulo\(\theta\), desde\(\theta=0\) hasta\(\theta=\theta_1\):
\ begin {align*} W&=\ int_0^ {\ theta_1} mGL\ sin\ theta d\ theta\\ &=mgL [-\ cos\ theta] _0^ {\ theta_1} =mGL (1-\ cos\ theta_1)\ end {align*}
b. Sabemos que el trabajo realizado por\(\vec F\) es\(W=mgL(1-\cos\theta_1)\). Entonces, queremos demostrar que\(L(1-\cos\theta_1)\) es igual a\(h\). Ampliando\(L(1-\cos\theta_1)\) da:
\ begin {align*} L (1-\ cos\ theta_1) &=L-L\ cos\ theta_1\ end {align*}
Esto se puede ilustrar en un diagrama, como en la Figura\(\PageIndex{6}\), que muestra que\(h\) es igual a\(L-L\cos\theta\).
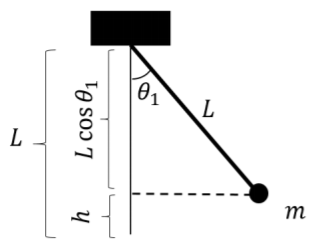
Figura\(\PageIndex{6}\): Diagrama que muestra la geometría del problema. Discusión:
La fuerza neta que actúa sobre la masa es igual a cero, por lo que el trabajo neto debe ser igual a cero. Las dos fuerzas que sí trabajan sobre la masa son la fuerza aplicada\(\vec F\), y la gravedad. El trabajo realizado por la fuerza aplicada si\(mgh\), así debe ser el trabajo realizado por gravedad\(-mgh\).