14.3: Olas en una cuerda

En esta sección, modelamos el movimiento de las ondas transversales sobre una cuerda, ya que esto proporciona una visión de muchas propiedades de las olas que se extienden a ondas que se propagan en otros medios.

Un pulso en una cuerda

Comenzamos modelando cómo un solo pulso se propaga por una cuerda horizontal que está bajo una tensión,$F_T$¹. Generalmente se considera que una onda es una serie regular de pulsos alternantes hacia arriba y hacia abajo que se propagan por la cuerda. Modelar la propagación de un pulso es así equivalente a modelar la propagación de una onda. La figura$\PageIndex{1}$ muestra cómo se puede generar un pulso en una cuerda horizontal enseñada levantando (y luego bajando) un extremo de la cuerda.

Figura$\PageIndex{1}$: (Izquierda:) Tirando hacia arriba y luego hacia abajo sobre una cuerda horizontal provoca que se forme un pulso y se propague. Después de un corto periodo de tiempo, se ve un pulso propagándose por la cuerda (derecha).

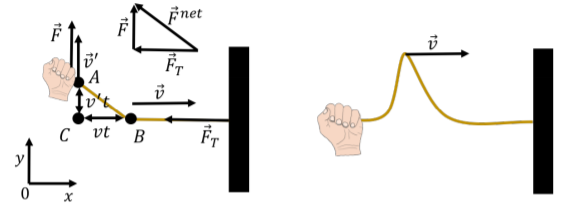
Podemos modelar la velocidad de propagación del pulso considerando la velocidad,$v$, del punto$B$ que se muestra en el panel izquierdo de la Figura$\PageIndex{1}$. Tenga en cuenta que el punto no$B$ es una partícula de la cuerda, y es, en cambio, la ubicación del “frente” de la perturbación que el pulso provoca en la cuerda. Modelamos la cuerda como estando bajo una fuerza horizontal de tensión,$\vec F_T$, y el pulso se inicia ejerciendo una fuerza vertical,$\vec F$, para mover el extremo (punto$A$) de la cuerda hacia arriba con una velocidad,$v'$. Así, al tirar hacia arriba de la cuerda con una fuerza,$\vec F$, a una velocidad$v'$, podemos iniciar una perturbación en la cuerda que se propagará con la velocidad$v$.

En poco tiempo,$t$, el punto$A$ de la cuerda se habrá movido hacia arriba una distancia$v't$, mientras que el punto se$B$ habrá movido a la derecha por una distancia$vt$. Si$t$ es lo suficientemente pequeño, podemos considerar los puntos$A$,$B$, y$C$ para formar las esquinas de un triángulo. Ese triángulo es similar al triángulo que se hace sumando vectorialmente la fuerza aplicada$\vec F$ y la tensión$\vec F_T$, como se muestra en la parte superior izquierda de la Figura$\PageIndex{1}$. En este caso, nos referimos al término de geometría “similar”, que describe dos triángulos que tienen los mismos ángulos. Así podemos escribir: $$\begin{aligned} \frac{F}{F_T}&=\frac{v't}{vt}=\frac{v'}{v}\\[4pt] \therefore F&= F_T \frac{v'}{v}\end{aligned}$$ Considera la sección de cuerda con longitud$vt$ que hemos levantado aplicando esa fuerza (suponemos que la distancia$AB$ es aproximadamente igual a la distancia$BC$). Si la cuerda tiene una masa por unidad de longitud$\mu$, entonces la masa del elemento de cuerda que se elevó (entre puntos$A$ y$B$) tiene una masa$m$,, dada por: $$\begin{aligned} m = \mu vt\end{aligned}$$ La componente vertical del impulso de esa sección de cuerda, con velocidad vertical dada por$v'$, es así: $$\begin{aligned} p = mv' = \mu vt v'\end{aligned}$$ Si la fuerza vertical,$\vec F$, se ejerció durante un periodo de tiempo$t$,, sobre el elemento de masa, le dará un impulso vertical$Ft$,, igual al cambio en la vertical momentum del elemento masa: $$\begin{aligned} Ft &= \Delta p \\[4pt] Ft &= \mu vt v'\\[4pt] \therefore F &= \mu v v'\end{aligned}$$ Podemos equiparar esta expresión$F$ con la obtenida de los triángulos similares para obtener una expresión para la velocidad,$v$, del pulso: $$\begin{aligned} \mu v v' &= F_T \frac{v'}{v}\\[4pt] \therefore v&= \sqrt{\frac{F_T}{\mu}}\end{aligned}$$ La velocidad de un pulso (y onda) que se propaga a través de una cuerda con lineal densidad de masa$\mu$, bajo una tensión,$F_T$, viene dada por:

$$v=\sqrt{\frac{F_{T}}{\mu}}$$

Si la tensión en la cuerda es mayor, el pulso se propagará más rápido. Si la densidad de masa lineal de la cuerda es mayor, entonces el pulso se propagará más lento.

Reflexión y transmisión

En esta sección, examinamos qué sucede cuando un pulso que viaja por una cuerda llega al final de la cuerda. Primero, considere el caso ilustrado en la Figura$\PageIndex{2}$ donde el extremo de la cuerda está fijado a una pared.

Figura$\PageIndex{2}$: Cuando el extremo de la cuerda se mantiene fijo, se invertirá el pulso reflejado.

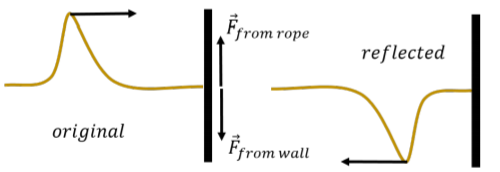
Cuando el pulso llega a la pared, la cuerda ejercerá una fuerza ascendente sobre la pared,$\vec F_{from\; rope}$. Por la Tercera Ley de Newton, el muro ejercerá entonces una fuerza hacia abajo sobre la cuerda,$\vec F_{from\; wall}$. La fuerza hacia abajo ejercida sobre la cuerda provocará que se forme un pulso descendente, y el pulso reflejado se invertirá en comparación con el pulso inicial que llegó a la pared.

Ahora, consideremos el caso cuando el extremo de la cuerda tiene un anillo unido a ella, de manera que pueda deslizarse libremente hacia arriba y hacia abajo de un poste, como se ilustra en la Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$: Cuando el extremo de la cuerda esté libre, el pulso reflejado estará en posición vertical.

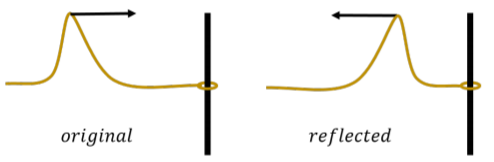
En este caso, el extremo de la cuerda se moverá hacia arriba a medida que llegue el pulso, lo que luego creará un pulso reflejado que está en la misma orientación que el pulso entrante.

Por último, considera un pulso que se propaga por una cuerda de masa por unidad de longitud$\mu_1$ que se ata a una segunda cuerda con masa por unidad de longitud$\mu_2$, que tienen la misma tensión. Cuando el pulso llega a la interfaz entre los dos medios (las dos cuerdas), parte del pulso se reflejará de nuevo, y parte se transmitirá al segundo medio (Figura$\PageIndex{4}$).

Figura$\PageIndex{4}$: Un pulso puede reflejarse y transmitirse a medida que cambia de medio. Panel izquierdo: El pulso se transmite de una cuerda más ligera a una cuerda más pesada. Panel derecho: El pulso se transmite de una cuerda más pesada a una cuerda más ligera.

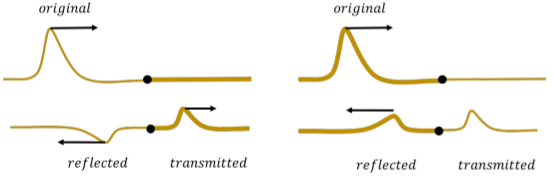
Al considerar las condiciones límite, se puede derivar el coeficiente de reflexión,$R$ (ver Ejercicio 14.10.2 para la derivación). Este coeficiente es la relación entre la amplitud del pulso reflejado y la amplitud del pulso inicial. Se encuentra que la relación es: $$\begin{aligned} R=\frac{\sqrt{\mu_1}-\sqrt{\mu_2}}{\sqrt{\mu_1}+\sqrt{\mu_2}}\end{aligned}$$ Cuando el pulso se mueve de una cuerda más ligera a una cuerda más pesada ($\mu_1<\mu_2$), el pulso reflejado se invertirá ($R<0$). Cuando el pulso pasa de una cuerda más pesada a una cuerda más ligera ($\mu_1>\mu_2$), el pulso reflejado permanecerá en posición vertical ($R>0$).

Cuando el extremo de la cuerda se fija a una pared (como en la Figura$\PageIndex{2}$), esto representa un caso limitante en el que la densidad de masa lineal del segundo material se acerca al infinito ($\mu_2 \rightarrow \infty$): $$\begin{aligned} R=\lim_{\mu_2\to \infty}\frac{\sqrt{\mu_1}-\sqrt{\mu_2}}{\sqrt{\mu_1}+\sqrt{\mu_2}}=\frac{-\sqrt{\mu_2}}{\sqrt{\mu_2}}=-1\end{aligned}$$ lo que significa que la amplitud del pulso reflejado tendrá la misma magnitud que el pulso inicial pero será en sentido contrario. Cuando el extremo de la cuerda está libre (Figura$\PageIndex{3}$), esto representa otro caso limitante, donde$\mu_2\rightarrow 0$: $$\begin{aligned} R=\lim_{\mu_2\to 0}\frac{\sqrt{\mu_1}-\sqrt{\mu_2}}{\sqrt{\mu_1}+\sqrt{\mu_2}}=\frac{\sqrt{\mu_1}}{\sqrt{\mu_1}}=1\end{aligned}$$ lo que significa que la amplitud del pulso reflejado estará en la misma dirección y tendrá la misma amplitud que el pulso inicial.

Ejercicio$\PageIndex{1}$

Una onda se propaga de una cuerda ligera a una cuerda más pesada que se une a la cuerda ligera (como el pulso ilustrado en la Figura$\PageIndex{4}$). ¿Qué puedes decir sobre la longitud de onda de la onda a ambos lados de la interfaz?

1. Es lo mismo en ambas secciones de cuerda.
2. La longitud de onda en la sección pesada de la cuerda es más larga.
3. La longitud de onda en la sección de luz de la cuerda es más larga.

Contestar

La ecuación de onda para una cuerda

En esta sección, mostramos cómo usar la Segunda Ley de Newton para derivar la ecuación de onda para ondas transversales que viajan por una cuerda con densidad de masa lineal$\mu$,, bajo tensión,$F_T$. Considere una pequeña sección de la cuerda, con masa y longitud$dm$$dx$, a medida que una ola pasa por esa sección de la cuerda, como se ilustra en la Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: Una pequeña sección de cuerda bajo tensión a medida que pasa una ola.

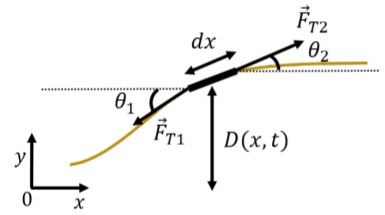
Suponemos que el peso del elemento de masa es insignificante en comparación con la fuerza de tensión que se encuentra en la cuerda. Así, las únicas fuerzas ejercidas sobre el elemento de masa son las de la tensión en la cuerda, tirando del elemento de masa desde cada lado, con fuerzas,$\vec F_{T1}$ y$\vec F_{T2}$. En general, las fuerzas de tensión a cada lado del elemento de masa tendrán diferentes direcciones y harán diferentes ángulos,$\theta$, con la horizontal, aunque su magnitud es la misma. Dejar$D(x,t)$ ser el desplazamiento vertical del elemento de masa ubicado en posición$x$. Podemos escribir el componente$y$ (vertical) de la Segunda Ley de Newton para el elemento de masa$dm$, como:

$$\begin{aligned} \sum F_y = F_{T2y} - F_{T1y} &= (dm)a_y\\[4pt] F_T\sin\theta_2 - F_T\sin\theta_1 &= dm \frac{\partial ^{2}D}{\partial t^{2}}\\[4pt] F_T(\sin\theta_2 - \sin\theta_1) &= dm \frac{\partial ^{2}D}{\partial t^{2}}\end{aligned}$$

donde se utilizó el hecho de que la fuerza de tensión tiene una magnitud,$F_T$, a cada lado del elemento de masa, y que la aceleración de la masa en la dirección vertical es la segunda derivada en el tiempo de$D(x,t)$, ya que para una onda transversal, esto corresponde a la $y$posición de una partícula. Ahora hacemos la aproximación de ángulo pequeño:

$$\begin{aligned} \sin\theta\approx \tan\theta = \frac{\partial D}{\partial x}\end{aligned}$$

en el que el seno del ángulo es aproximadamente igual a la tangente del ángulo, que es igual a la pendiente de la cuerda. Aplicando esta aproximación a la Segunda Ley de Newton:

$$\begin{aligned} F_T\left(\frac{\partial D}{\partial x}\Bigr|_{right} - \frac{\partial D}{\partial x}\Bigr|_{left}\right) &= dm \frac{\partial ^{2}D}{\partial t^{2}}\end{aligned}$$

donde indicamos que el término entre paréntesis es la diferencia en la pendiente de la cuerda entre el lado derecho y el lado izquierdo del elemento de masa. Si la cuerda tiene densidad de masa lineal$\mu$, entonces la masa del elemento de cuerda se puede expresar en términos de su longitud,$dx$: $$\begin{aligned} dm = \mu dx\end{aligned}$$

Reemplazar$dm$ en la ecuación da:

$$\begin{aligned} F_T\left(\frac{\partial D}{\partial x}\Bigr|_{right} - \frac{\partial D}{\partial x}\Bigr|_{left}\right) &= \mu dx \frac{\partial ^{2}D}{\partial t^{2}}\\[4pt] F_T\left(\frac{\frac{\partial D}{\partial x}\Bigr|_{right} - \frac{\partial D}{\partial x}\Bigr|_{left}}{dx}\right) &= \mu \frac{\partial ^{2}D}{\partial t^{2}}\end{aligned}$$

El término entre paréntesis es la diferencia en las primeras derivadas de$D(x,t)$ con respecto a$x$, dividida por la distancia,$dx$, entre las que se evalúan esas derivadas. Esta es precisamente la definición de la segunda derivada con respecto a$x$, por lo que podemos escribir:

$$\begin{aligned} F_T \frac{\partial ^{2}D}{\partial x^{2}} &= \mu \frac{\partial ^{2}D}{\partial t^{2}}\\[4pt] \therefore \frac{\partial ^{2}D}{\partial x^{2}} &= \frac{\mu}{F_T} \frac{\partial ^{2}D}{\partial t^{2}}\\[4pt]\end{aligned}$$

que es precisamente la ecuación de onda:

$$\begin{aligned} \frac{\partial ^{2}D}{\partial x^{2}} &= \frac{1}{v^2} \frac{\partial ^{2}D}{\partial t^{2}}\\[4pt]\end{aligned}$$

con velocidad: $$\begin{aligned} v&= \sqrt{\frac{F_T}{\mu}}\end{aligned}$$ como encontramos anteriormente. Así, encontramos que la velocidad de propagación de la onda está relacionada con la dinámica de modelar el sistema, y no está relacionada con la onda misma.

Notas al pie

1. No utilizamos T para la tensión, para no confundir con el periodo de una ola.