14.5: Energía Transportada por una Ola

En esta sección, examinamos cómo modelar la energía que es transportada por las olas. Aunque ningún material se mueve junto con una ola, la energía mecánica puede ser transportada por una ola, como lo demuestra el daño causado por las olas de un sismo.

Una onda como estar hecha de simples osciladores armónicos

Considera una onda que se propaga a través de un medio. Podemos modelar el movimiento de una de las partículas en el medio como si fuera el movimiento de un simple oscilador armónico ¹. Esto se ilustra en la Figura\(\PageIndex{1}\), que muestra el desplazamiento en función del tiempo para un punto en el medio ubicado en el origen cuando una ola pasa por ese punto. El desplazamiento de ese punto, en\(x=0\), si así lo elegimos\(\phi=0\), viene dado por:

\[\begin{aligned} D(x=0,t) = A\sin(-\omega t)\end{aligned}\]

Figura\(\PageIndex{1}\): El desplazamiento en función del tiempo para una partícula en el medio (at\(x = 0\)) es idéntico al movimiento de un simple oscilador armónico.

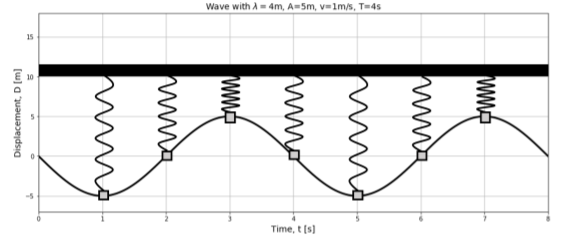
El desplazamiento de la partícula en el medio se describe mediante la misma ecuación que la posición de un oscilador armónico simple, con la misma frecuencia angular\(\omega\), que la de la onda.

También podemos ver una instantánea de la onda en el tiempo, y modelar los diferentes puntos en el medio como diferentes osciladores que tienen diferentes desplazamientos. Esto se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): El desplazamiento en función de la posición para diferentes puntos en un medio. Cada punto en el medio se puede modelar como un simple oscilador armónico.

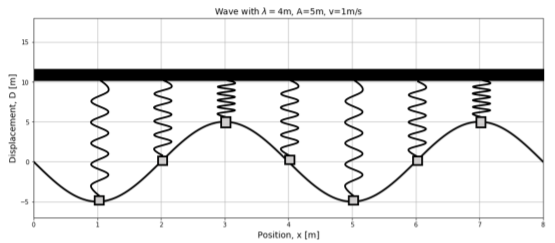
Energía transportada en una onda unidimensional

En esta sección, mostramos cómo describir la energía transportada por una ola unidimensional a lo largo de una cuerda. Modelamos cada partícula en la cuerda a través de la cual la onda se propaga como un pequeño oscilador armónico simple con masa\(m\), unido a un resorte con una constante de resorte efectiva,\(k_s\)².

Por supuesto, no hay resorte real, pero aún podemos determinar una constante de resorte efectiva,\(k_s\), a partir de la frecuencia angular:\[\begin{aligned} \omega &= \sqrt{\frac{k_s}{m}}\\ \therefore k_s &= \omega^2 m\end{aligned}\] que corresponde a la constante de resorte que daría la frecuencia angular correcta para la partícula de masa\(m\).

La energía mecánica total de un oscilador,\(E_m\), se puede evaluar cuando el oscilador se encuentra en su desplazamiento máximo,\(A\), desde su equilibrio, donde su energía cinética es cero:\[\begin{aligned} E_m = \frac{1}{2}k_s A^2 = \frac{1}{2}\omega^2 m A^2\end{aligned}\]

Si la cuerda es infinitamente larga, y lleva una onda continua, tendrá una cantidad infinita de energía, ya que corresponderá a un número infinito de osciladores. En cambio, calculemos cuánta energía,\(E_\lambda\), se almacena en la onda a lo largo de una longitud de onda,\(\lambda\). Para ello, necesitamos evaluar cuántos osciladores efectivos están contenidos en la cuerda, a una distancia\(\lambda\), para que podamos sumar todas sus energías juntas para obtener la energía almacenada en una longitud de onda:\[\begin{aligned} E_\lambda = \sum \frac{1}{2}\omega^2 m A^2\end{aligned}\] donde la suma está sobre el número de osciladores en una longitud de onda. Por supuesto, la cuerda en realidad no está hecha de osciladores, pero podemos modelar cada sección de cuerda de longitud que\(dx\) tiene siendo un oscilador de masa\(dm=\mu dx\), donde\(\mu\) está la densidad de masa lineal de la cuerda. La suma (integral) de la energía de los osciladores sobre una longitud de onda se puede escribir así como:\[\begin{aligned} E_\lambda = \int_0^\lambda \frac{1}{2}\omega^2 \mu A^2 dx = \frac{1}{2}\omega^2 \mu A^2 \lambda\end{aligned}\] La energía almacenada en una longitud de onda no es una propiedad muy útil de una onda, ya que la energía total en la onda depende de la longitud de la onda. Podemos describir la velocidad a la que la energía es transmitida por la onda (su potencia), ya que sabemos cuánto tiempo,\(T\), le llevará a la onda viajar una longitud de onda, y solo determinamos cuánta energía se almacena en una longitud de onda. La potencia promedio con la que la energía es transportada por una ola viene dada por:\[\begin{aligned} P = \frac{E_\lambda}{T} = \frac{\frac{1}{2}\omega^2 \mu A^2 \lambda}{T}=\frac{1}{2}\omega^2 \mu A^2 v\end{aligned}\] dónde\(T\) está el periodo de la ola, y\(v=\lambda/T\) es la velocidad de la ola. La potencia transmitida por una ola en una cuerda viene dada por:

\[P=\frac{1}{2}\omega ^{2}\mu A^{2}v\]

Podemos ver que la potencia transmitida por una onda va como la amplitud,\(A\), de la onda al cuadrado. Se necesita así cuatro veces más energía para duplicar la amplitud de las olas que se envían por una cuerda.

Energía transportada en una onda esférica, tridimensional

En esta sección, te mostramos cómo modelar la velocidad a la que se transporta la energía en ondas tridimensionales esféricas, como las ondas sonoras que se generan al aplaudir. Una onda sonora esférica es una perturbación de presión en el aire que se propaga esféricamente hacia afuera desde un punto de emisión. Podemos pensar en conchas esféricas delgadas que contienen aire que se expanden y contraen sobre su posición de equilibrio a medida que la ola se mueve a través de las conchas El movimiento de cada proyectil es similar al de un simple oscilador armónico de masa\(dm\), donde\(dm\) está la masa de aire en la concha oscilante.

Figura\(\PageIndex{3}\): Izquierda: Dividimos el aire en conchas esféricas delgadas. Aquí representamos tres conchas (los círculos negros). Centro: Cuando aplaudes, se le da energía al caparazón más interior y se expande. Derecha: La energía se transfiere al siguiente proyectil, que se expande a medida que se contrae el primer proyectil. Es así como la onda se propaga hacia afuera. Cuando los proyectiles están más cerca entre sí, las moléculas de aire están más cerca entre sí y ejercen una presión que intenta expandir el caparazón.

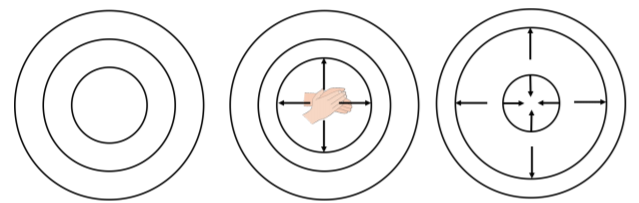
Considere un caparazón en una posición radial\(r\),, desde la fuente, con espesor\(dr\) y masa\(dm\):

Figura\(\PageIndex{4}\): Una concha esférica en posición radical\(r\) con espesor\(dr\).

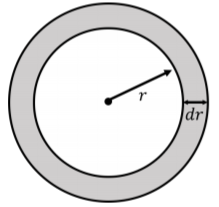
Si el medio tiene una densidad\(\rho\), entonces la masa de la concha viene dada por:\[\begin{aligned} dm = \rho dV = \rho 4\pi r^2 dr\end{aligned}\] donde\(dV = 4\pi r^2 dr\) esta el volumen de la concha. Nuevamente, si modelamos cada shell como un simple oscilador armónico con masa\(dm\), entonces la energía\(dE\),, almacenada en esa concha oscilante viene dada por:\[\begin{aligned} dE = \frac{1}{2}k_s A^2 = \frac{1}{2}\omega^2 dm A^2 = \frac{1}{2}\omega^2 A^2 \rho 4\pi r^2 dr=2\pi\rho \omega^2 A^2 r^2 dr\end{aligned}\] dónde\(\omega\) está la frecuencia angular de la onda, y\(A\) es la amplitud de la ola. Expresamos la constante de resorte efectiva\(k_s\), en términos de la frecuencia angular del oscilador armónico simple y su masa, como hicimos en el apartado anterior. Ahora tiene menos sentido determinar la energía que se almacena en una longitud de onda de la onda porque la energía,\(dE\), almacenada en un caparazón depende de la ubicación,\(r\), de esa concha. Este no fue el caso de una onda unidimensional, donde la energía almacenada en un oscilador no dependía de la posición de ese oscilador.

La velocidad a la que la energía es transportada por la ola viene dada por:\[\begin{aligned} P = \frac{dE}{dt}\end{aligned}\] Podemos usar la Regla de Cadena para cambiarla en una derivada sobre\(r\):\[\begin{aligned} P = \frac{dE}{dr}\frac{dr}{dt}=\frac{dE}{dr}v\end{aligned}\] dónde\(\frac{dr}{dt}=v\) está la velocidad de la ola (la tasa de cambio del radio de una concha). La potencia transmitida por la onda esférica viene así dada por:\[\begin{aligned} P &=\frac{dE}{dr}v =2\pi\rho \omega^2 A^2 r^2 v\end{aligned}\] donde la potencia parece depender de qué tan lejos estés de la fuente (\(r\)).

Supongamos que tiene un\(50\text{W}\) altavoz emitiendo sonido; cada carcasa radial que emana del altavoz debe transportar energía a una velocidad de\(50\text{W}\). Esto es simplemente una afirmación de que la energía irradiada por el hablante tiene que pasar de un caparazón a otro y ser conservada. Dado que la potencia transportada por un proyectil parece depender del radio del proyectil, si la potencia transmitida por cada proyectil es la misma, entonces la amplitud de la onda en cada proyectil debe disminuir, de manera que la potencia no dependa realmente del radio del proyectil. En particular, para una onda esférica, la amplitud disminuirá en función de la distancia desde la fuente:\[\begin{aligned} P& = \text{constant}\\ \therefore A&=\frac{1}{r}\sqrt{\frac{P}{2\pi\rho \omega^2 v}}\end{aligned}\] Esto es muy diferente de la propagación de una onda unidimensional, en la que la amplitud no cambia con la distancia. En la práctica, si hay pérdidas de energía por, digamos, fricción, entonces la amplitud de una onda unidimensional también disminuiría con la distancia desde la fuente, pero este es un efecto diferente.

Pensamientos de Olivia

Aquí hay una forma ligeramente diferente de pensar por qué la amplitud de la onda disminuye a medida que se aleja de la fuente. Cuando una onda esférica viaja hacia afuera, la energía pasa de un caparazón a otro. Las conchas exteriores son más grandes que las conchas internas, por lo que contendrán más partículas. Debido a la conservación de la energía, cuando la energía se transfiere de un caparazón a otro, la energía total permanece igual. En las envolturas externas, la energía debe ser compartida entre un mayor número de partículas, por lo que cada partícula obtiene menos energía, y por lo tanto oscila con una amplitud menor que las partículas de la capa anterior.

Para recordar esto, imagina que las conchas en Figura\(\PageIndex{3}\) son círculos de niños parados uno al lado del otro. El círculo más íntimo tiene\(10\) hijos y el círculo más externo tiene\(100\) hijos. Si tienes\(100\) caramelos, y se los das a los niños en el círculo más íntimo, cada uno conseguirá\(10\) así que se pondrán muy hiper y comenzarán a saltar mucho. Si en cambio le das\(100\) los caramelos a los niños del círculo más externo, cada uno solo obtendrá uno. Los niños solo se pondrán un poco hiper y saltarán menos.

La “intensidad de una onda”,\(I\), se define como la potencia por unidad de área que es transmitida por la onda. Para un frente de onda esférica en posición radial\(r\), con área\(4\pi r^2\), la intensidad de la onda se define como:\[\begin{aligned} I = \frac{P}{4\pi r^2} = \frac{1}{2}\rho \omega^2 A^2 v\end{aligned}\]

Por lo general, la intensidad de una ola es algo que se puede medir, ya que corresponde a la potencia entregada a algún dispositivo de medición con una superficie conocida. Por ejemplo, no podemos medir directamente la potencia total que transportan las olas de un sismo, ya que necesitaríamos un instrumento que pudiera abarcar toda la onda resultante. En cambio, podemos medir la intensidad de las olas del terremoto midiendo cuánta energía se entrega a algún instrumento con una superficie conocida. Al conocer nuestra distancia del sismo, podríamos entonces determinar la potencia total de salida del sismo.

La intensidad es una medida de cuánta energía es entregada por unidad de área por una ola y baja como el cuadrado de la distancia desde la fuente (ya\(A\propto 1/r\)). Si la fuente de la ola es un terremoto, entonces tu casa tendrá cuatro veces menos daños que la de tu amigo, si tu casa está ubicada solo el doble del epicentro que la de tu amigo.Te causarás cuatro veces menos daños en tus oídos si te mueves solo el doble del escenario en un concierto de rock.

Notas al pie

1. Si el medio tiene una fuerza restauradora lineal o si la amplitud de las oscilaciones es pequeña.

2. Utilizamos\(k_{s}\) para la constante de resorte, para distinguirla\(k\), el número de onda.