17.3: Cargos en un Conductor

Podemos usar la Ley de Gauss para entender cómo se arreglan los cargos en un conductor. Consideremos (de nuevo) un plano infinito que lleve una carga total por unidad de área,\(\sigma\), similar a lo que consideramos en el Ejemplo 17.2.3. En este caso, consideramos explícitamente que el plano es un conductor y tiene un espesor finito. Si nos acercamos al plano, podemos ilustrar que las cargas se encuentran en la superficie del plano, como se ilustra en la Figura\(\PageIndex{1}\), donde se ve el plano de borde en. Así, la densidad de carga en la superficie es la mitad de la densidad de carga total del plano.

Figura\(\PageIndex{1}\): Sección transversal de un plano conductor donde las cargas migran a la superficie. También se muestra una superficie gaussiana en forma de caja vista desde el lado (la tercera dimensión de la caja es perpendicular al plano de la página).

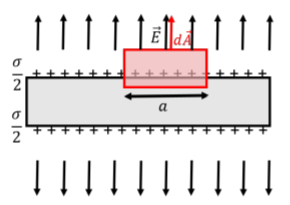
Para determinar el campo eléctrico cerca del plano, elegimos una superficie gaussiana que sea una caja (como en el Ejemplo 17.2.3), pero requerimos que el extremo inferior de la caja pase por el plano, como se ilustra en la Figura\(\PageIndex{1}\). Con esta elección de superficie gaussiana, solo la superficie superior (área\(a^2\)) tendrá flujo a través de ella, ya que el campo eléctrico dentro de un conductor debe ser cero ¹. El flujo total viene dado por:\[\begin{aligned} \oint \vec E\cdot d\vec A&= \int_{top} EdA=Ea^2\end{aligned}\] La carga encerrada viene dada por:\[\begin{aligned} Q^{enc}=\frac{\sigma}{2}a^2\end{aligned}\] donde utilizamos el hecho de que solo la mitad de las cargas están dentro del volumen encerrado por nuestra superficie gaussiana, de manera que la carga por unidad de área es la mitad (\(\frac{\sigma}{2}\)) de eso para todo el plano. Aplicando la Ley de Gauss, encontramos que el campo eléctrico viene dado por:\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\ Ea^2&= \frac{\sigma a^2}{2\epsilon_0}\\ \therefore E&= \frac{\sigma}{2\epsilon_0}\quad \text{(Field above an infinite plane)}\end{aligned}\] como antes, pero el factor de 2 ahora vino de la densidad de carga, más que del hecho de que dos de las caras de la caja tenían flujo distinto de cero (como fue el caso en el Ejemplo 17.2.3). Podemos generalizar este resultado para determinar el campo eléctrico cerca de la superficie de cualquier conductor. Muy cerca de la superficie de cualquier objeto, se puede considerar que la superficie es similar a un plano infinito. Si esa superficie lleva carga por unidad de área\(\sigma\), entonces el campo eléctrico justo encima de la superficie viene dado por:\[\begin{aligned} E&= \frac{\sigma}{\epsilon_0} \quad \text{(Field near a conducting surface)}\end{aligned}\] En este caso, no hay factor de 2, porque la densidad de carga en esta ecuación es la densidad de carga del conductor (no la densidad de carga a un lado del superficie). En la ecuación anterior, la densidad de carga en la superficie del plano conductor fue\(\frac{\sigma}{2}\).

Consideremos, ahora, un caparazón conductor esférico neutro, como se muestra desde el lado en el panel izquierdo de la Figura\(\PageIndex{2}\). Cuando una carga,\(+Q\), se coloca en el centro del proyectil (panel derecho), las cargas dentro del proyectil se moverán hasta que el campo dentro del material conductor del proyectil sea idéntico cero. Las cargas negativas se moverán hacia la superficie interna (ya que son atraídas\(+Q\)) y las cargas positivas serán repelidas sobre la superficie exterior, bajo la influencia del campo eléctrico creado por\(+Q\) (mostrado en el diagrama como\(\vec E_{Q}\)). Eventualmente, la separación de cargas conducirá a un campo eléctrico (mostrado en el diagrama como\(\vec E_{\sigma}\)) en la dirección opuesta. Las cargas dejarán de moverse una vez que el campo eléctrico total en el conductor sea cero (cuando los dos campos se cancelan exactamente en todas partes del conductor).

Figura\(\PageIndex{2}\): Izquierda: un caparazón esférico conductor neutro (visto borde encendido). Derecha: Una carga positiva\(+Q\),, colocada en el centro del caparazón. Las cargas en el caparazón se separarán para mantener el campo eléctrico dentro del conductor cero.

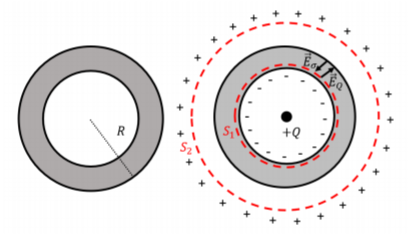
Podemos usar la Ley de Gauss para determinar la cantidad de carga que se ha acumulado en la superficie interna. Considera la superficie esférica gaussiana\(S_1\),, en la Figura\(\PageIndex{2}\), que es concéntrica con la concha y tiene un radio tal que la superficie se encuentra justo dentro de la concha. Dado que el campo eléctrico es cero dentro de la carcasa, el flujo que sale de la superficie gaussiana debe ser cero. Por Ley de Gauss, la cantidad de carga encerrada por la superficie también debe ser cero. Así, una carga total,\(-Q\), se habrá acumulado en la superficie interna del conductor (ya que\(Q^{enc}=-Q+Q=0\)). Debido a que no se puede simplemente crear carga a partir de la nada, debe haber una cantidad igual de carga opuesta\(+Q\),, en la superficie exterior del caparazón. Esto es cierto para cualquier material conductor con una cavidad en su interior: si colocas una carga\(+Q\) en la cavidad, una carga,\(-Q\) se acumulará en la superficie interna y una carga,\(+Q\), se acumulará en la superficie exterior.

Si ahora consideramos el flujo que sale de la superficie,\(S_2\), fuera del caparazón, la carga neta encerrada será\(Q^{enc}=+Q-Q+Q=+Q\). El flujo que sale de la superficie esférica del radio, digamos\(r\), viene dado entonces por:\[\begin{aligned} \oint \vec E\cdot d\vec A &= E(4\pi r^2)\\\end{aligned}\] y el campo eléctrico, de la Ley de Gauss, es simplemente el de una carga puntual,\(+Q\):\[\begin{aligned} E&=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\end{aligned}\] y la concha no tiene ningún efecto sobre el campo en regiones donde no hay material conductor del caparazón. Justo en la superficie de la concha (radio exterior,\(R\)), la densidad de carga superficial viene dada por:\[\begin{aligned} \sigma=\frac{Q}{4\pi r^2}\end{aligned}\] Arriba, encontramos el campo eléctrico en la superficie de un conductor que transporta carga por unidad de área\(\sigma\),, ser:\[\begin{aligned} E&= \frac{\sigma}{\epsilon_0}\end{aligned}\] que es claramente el mismo resultado que obtuvimos usando la superficie esférica,\(S_2\):\[\begin{aligned} E&= \frac{\sigma}{\epsilon_0}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\end{aligned}\] Obsérvese que encontramos el campo eléctrico usando la Ley de Gauss solo en este último caso, y encontramos que era igual al campo eléctrico que se obtiene de la ley de Coulomb. Así, la Ley de Gauss sólo funciona si el campo tiene una dependencia de “ley cuadrada inversa”. Si la Ley de Gauss no proporciona el campo eléctrico correcto, entonces la fuerza no depende de ello\(1/r^2\). La Ley de Gauss se puede utilizar para hacer pruebas extremadamente estrictas de si la fuerza va como\(1/r^2\) o se desvía de este modelo.

Notas al pie

1. Dado que las cargas pueden moverse libremente en un conductor, se moverán hasta que no haya razón para moverse. Eventualmente, las cargas se acumulan de tal manera que el campo neto en el conductor es cero. Para un avión, esto significa que la mitad de las cargas se moverán a cada lado, como se ilustra.