20.8: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

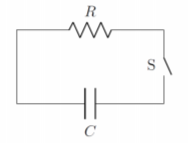
Un circuito RC simple como se muestra en la Figura\(\PageIndex{1}\) contiene un condensador cargado de capacitancia desconocida\(C\),, en serie con una resistencia,\(R=2\Omega\). Cuando se carga, la diferencia de potencial entre los terminales del condensador es\(9\text{V}\).

En el momento\(t=0\text{s}\), el interruptor,\(S\), está cerrado, permitiendo que el condensador se descargue a través de la resistencia. Luego se mide la corriente para que esté\(I = 0.05\text{A}\) en\(t = 5\text{s}\) después de abrir el interruptor.

1. ¿Cuál es la capacitancia del condensador?
2. ¿A qué carga aguantó el condensador\(t = 2\text{s}\)?

Figura\(\PageIndex{1}\): Un circuito simple con una resistencia y un condensador.

Contestar

a. En este caso, el condensador se está descargando en función del tiempo. En el momento\(t=0\), el voltaje a través del condensador es\(\Delta V=9\text{V}\). Podemos modelar este circuito de descarga de manera similar a como modelamos el circuito de carga.

Comenzamos con la regla de unión de Kirchhoff, que conduce a una ecuación diferencial para la carga almacenada en el condensador\(Q(t)\),, en función del tiempo:\[\begin{aligned} \Delta V - IR &=0\\ \frac{Q}{C} - IR &=0\\ \frac{Q}{C} - \frac{dQ}{dt}R &=0\\ \therefore \frac{dQ}{dt} = -\frac{1}{RC}Q\end{aligned}\] Esta ecuación diferencial es sencilla de resolver, ya que dice que la derivada de\(Q(t)\) es igual a un constante multiplicada por\(Q(t)\). Así,\(Q(t)\), debe ser una función exponencial:\[\begin{aligned} Q(t) = Q_0 e^{-\frac{t}{RC}}\end{aligned}\] donde,\(Q_0\), es la carga (desconocida) en el condensador a\(t=0\). Se puede verificar fácilmente que tomar la derivada de esta ecuación dará como resultado que la ecuación diferencial sea satisfecha.

La corriente,\(I(t)\), en función del tiempo viene dada por:\[\begin{aligned} I &=\frac{dQ}{dt}=-\frac{1}{RC}Q=\frac{Q_0}{RC} e^{-\frac{t}{RC}}=I_0e^{-\frac{t}{RC}}\end{aligned}\] donde\(I_0=\frac{Q_0}{RC}\) esta la corriente en\(t=0\).

También sabemos que la corriente a través de la resistencia at\(t=0\) viene dada por la Ley de Ohm, ya que, en ese momento, el voltaje,\(\frac{Q_0}{C}=9\text{V}\):\[\begin{aligned} I_0=\frac{Q_0}{RC}=\frac{(9\text{V})}{(2\Omega)}=4.5\text{A}\end{aligned}\]

Entonces sabemos que la corriente, en el tiempo\(t=5\text{s}\), es igual a\(I(5)=0.05\text{A}\), lo que nos permite determinar la capacitancia:\[\begin{aligned} I(5)&=I_0e^{-\frac{t}{RC}}\\ \ln\left( \frac{I(5)}{I_0} \right)&=-\frac{t}{RC}\\ \therefore C&=\frac{t}{R \ln\left( \frac{I_0}{I(5)} \right)}=\frac{(5\text{s})}{(2\Omega)\ln\left( \frac{(4.5\text{A})}{(0.05\text{A})} \right)}=0.56\text{F}\end{aligned}\]

b. para encontrar la carga almacenada en el condensador en\(t = 2\text{s}\), podemos usar la función\(Q(t)\) que determinamos antes:\[\begin{aligned} Q(t=2\text{s})=Q_0 e^{-\frac{t}{RC}}\end{aligned}\] donde podemos determinar,\(Q_0\), ahora que conocemos la capacitancia. \(Q_0\)es la carga en el condensador en el momento\(t=0\), cuando el voltaje a través del condensador es\(9\text{V}\):\[\begin{aligned} Q_0=C\Delta V = (0.56\text{F})(9\text{V})=5.0\text{C}\end{aligned}\] At\(t = 2\text{s}\), la carga en el condensador es así:\[\begin{aligned} Q(t = 2\text{s})=(5.0\text{C})e^{-\frac{(2\text{s})}{(2\Omega)(0.56\text{F})}}=0.84\text{C}\end{aligned}\]

Ejercicio\(\PageIndex{2}\)

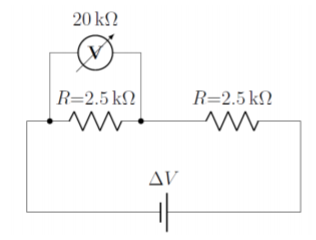
Un voltímetro con una resistencia de\(R_V = 20\text{k}\Omega\) está unido a un circuito con una batería de voltaje desconocido y dos resistencias con una resistencia de\(R = 2.5\text{k}\Omega\) como se muestra en la Figura\(\PageIndex{2}\). El voltímetro lee que la caída de voltaje sobre una de las resistencias es\(\Delta V_{vm} =5.647\text{V}\). ¿Cuál es la caída de voltaje\(V_R\),, sobre cada resistor cuando se retira el voltímetro del circuito?

Figura\(\PageIndex{2}\): Un circuito con una batería de voltaje desconocido.

Contestar

Para conocer el voltaje a través de una de las resistencias, necesitamos determinar el voltaje que está a través de la batería. Una vez que hayamos determinado el voltaje a través de la batería, el voltaje a través de una de las resistencias solo será la mitad de ese a través de la batería, ya que las dos resistencias tienen la misma resistencia.

Podemos modelar el circuito con el voltímetro en su lugar, ya que conocemos el voltaje a través de la combinación paralela del voltímetro y la resistencia (ese voltaje que es leído por el voltímetro). Podemos combinar el voltímetro y una de las resistencias en una resistencia equivalente,\(R_{eff}\):\[\begin{aligned} R_{eff} &= \frac{1}{R_V^{-1}+R^{-1}}\\ R_{eff} &= \frac{1}{(20\text{k}\Omega)^{-1}+(2.5\text{k}\Omega)^{-1}}\\ R_{eff} &= 2.22\text{k}\Omega\\\end{aligned}\] Ahora que tenemos la resistencia efectiva así como la caída de voltaje a través de esa resistencia efectiva, podemos resolver la corriente a través del circuito:\[\begin{aligned} I &= \frac{\Delta V_{vm}}{R_{eff}}\\ I &= \frac{5.647\text{V}}{2.22\text{k}\Omega}\\ I &= 2.541\text{mA}\\\end{aligned}\] Ahora que tenemos la corriente a través del circuito, podemos determinar la caída de voltaje a través de la segunda resistencia. Al agregar esa caída de voltaje al voltaje conocido a través de la resistencia efectiva, podemos determinar el voltaje de la batería:\[\begin{aligned} \Delta V_{battery} &= I(R_{eff}+R)\\ \Delta V_{battery} &= (2.541\text{mA})(2.222\text{k}\Omega+2.5\text{k}\Omega)\\ \Delta V_{battery} &= 12\text{V}\\\end{aligned}\] Así, sin voltímetro presente, el voltaje a través de cada resistencia es\(6\text{V}\).