21.3: La fuerza magnética sobre un cable portador de corriente.

revisar temas

Sección 19.2 sobre el modelo microscópico de corriente.

En esta sección, examinamos la fuerza que ejerce un campo magnético sobre un cable que transporta corriente eléctrica. Dado que una corriente se forma por cargas móviles, es natural esperar que un cable que transporta corriente experimente una fuerza si se sumerge en un campo magnético.

Considere un alambre vertical con área de sección transversal,$A$, transportando corriente,$I$, hacia arriba que se sumerge en un campo magnético uniforme,$\vec B$, en la página, como se ilustra en la Figura$\PageIndex{1}$. Dentro del alambre, en promedio, los electrones tienen una velocidad de deriva$\vec v_d$,, en dirección descendente (ya que se mueven en dirección opuesta a la de la corriente convencional).

Figura$\PageIndex{1}$: Una sección de alambre lleva corriente convencional$I$, hacia arriba mientras se sumerge en un campo magnético uniforme,$\vec B$, en la página. Se introduce el vector,$\vec l$, para representar una sección de alambre de longitud$l$ transportando corriente en la dirección de$\vec l$.

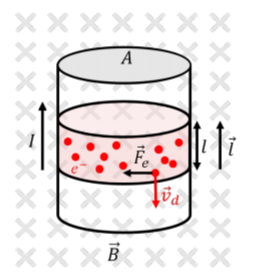
Un solo electrón (con carga$q=-e$) experimentará una fuerza magnética,$\vec F_e$, dada por:

$$\begin{aligned} \vec F_e = -e \vec v_d \times \vec B\end{aligned}$$ como se ilustra en la Figura$\PageIndex{1}$. Una sección de alambre de longitud,$l$, contendrá electrones$N=nAl$ a la deriva, donde$n$ está la densidad de electrones libres para el cable (el número de electrones por unidad de volumen que están disponibles para producir una corriente). Así, la fuerza magnética en esa sección de alambre será$N$ multiplicada por la fuerza sobre un solo electrón: $$\begin{aligned} \vec F = N\vec F_e = nAl (-e \vec v_d \times \vec B)=-nAle \vec v_d \times \vec B\end{aligned}$$ Recordemos el modelo microscópico de corriente para relacionar la velocidad de deriva con la corriente convencional en el cable: $$\begin{aligned} I &= -nAev_d\end{aligned}$$ donde el signo menos indica que los electrones negativos fluyen en dirección opuesta a la corriente convencional. También se introduce un vector,$\vec l$, con una magnitud igual a la longitud de la sección de alambre, y una dirección que es paralela a la corriente convencional (por lo tanto antiparalela a la velocidad de deriva de electrones). La fuerza sobre la sección de la longitud$l$,, del alambre viene así dada por:

$$\begin{aligned}\vec F=-nAle\vec v_{d}\times \vec B \end{aligned}$$

$$\vec F=I\vec l\times \vec B$$

Ejercicio$\PageIndex{1}$

Figura$\PageIndex{2}$: Un cable portador de corriente que se mueve a través de un campo magnético.

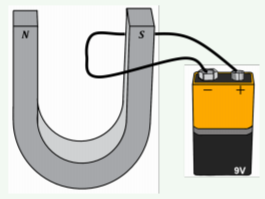
¿En qué dirección apunta la fuerza magnética sobre el cable portador de corriente que se coloca en el campo magnético entre los polos del imán de herradura que se muestra en la Figura$\PageIndex{2}$?

1. Arriba.
2. Abajo.
3. En la página.
4. Fuera de la página.

Contestar

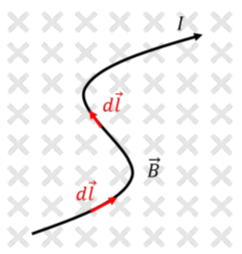
Tenga en cuenta que si el cable no es recto, entonces podemos modelar el cable como hecho de muchas secciones infinitesimalmente cortas (Figura$\PageIndex{3}$), de longitud$dl$, y sumar las fuerzas en esas secciones para obtener la fuerza total en una sección de longitud,$L$:

$$\begin{aligned} \vec F = \int_0^L I d\vec l \times \vec B\end{aligned}$$

Figura$\PageIndex{3}$ La fuerza magnética sobre un cable curvo portador de corriente se obtiene modelando las fuerzas ejercidas sobre secciones infinitesimales de alambre, cada una con longitud$d\vec l$, y sumando esas fuerzas para obtener la fuerza total sobre el alambre.

Ejemplo$\PageIndex{1}$

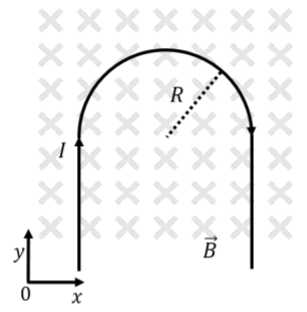
Un cable que transporta corriente$I$,, se dobla de manera que tenga una sección semicircular con radio$R$, como se muestra en la Figura$\PageIndex{4}$. El alambre se sumerge en un campo magnético uniforme$\vec B$,, que es perpendicular al plano del alambre, como se muestra. Usando el sistema de coordenadas dado, ¿cuál es la fuerza neta en el cable?

Figura$\PageIndex{4}$: Un cable portador de corriente con sección semicircular se sumerge en un campo magnético uniforme.

Solución:

Podemos modelar el alambre como hecho de tres secciones: una sección recta que transporta corriente en la$y$ dirección positiva, una sección curva y otra sección recta que transporta corriente en la$y$ dirección negativa.

Considera la primera sección recta, llevando corriente en la$y$ dirección positiva. La fuerza sobre esa sección de alambre, por la regla de la derecha, será hacia la izquierda ($x$dirección negativa):

$$\begin{aligned} F_S &= I \vec l \times \vec B\\ &= I (l\hat y) \times (-B\hat z)\\ &= -IlB (\hat y \times \hat z)=-IlB\hat x\end{aligned}$$ donde,$l$, es la longitud (desconocida) de esa sección de alambre. La fuerza ejercida sobre la otra sección recta del alambre tendrá la misma magnitud, pero la dirección opuesta (ya que la corriente, y por lo tanto el vector$\vec l$, está en la dirección opuesta). Así, las fuerzas de las dos secciones rectas del alambre se cancelan, como se ilustra en la Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: La fuerza magnética en diferentes secciones de alambre.

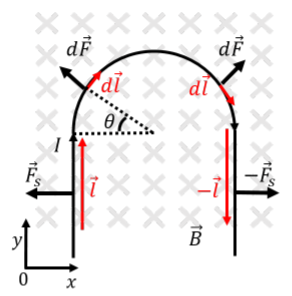
Para calcular la fuerza ejercida sobre la sección semicircular, necesitamos sumar las fuerzas ejercidas sobre las secciones infinitesimales del alambre que conforman esa sección. Consideremos la fuerza magnética sobre las dos secciones infinitesimales ilustradas en la Figura$\PageIndex{5}$. Los$x$ componentes de las fuerzas se cancelarán, mientras que los$y$ componentes se sumarán. Así, por simetría, anticipamos que la fuerza neta sobre la sección semicircular estará en la$y$ dirección positiva.

Considere la pequeña fuerza sobre la sección de alambre ubicada en ángulo,$\theta$, como se ilustra en la Figura$\PageIndex{5}$. Podemos escribir el vector$d\vec l$ como:

$$\begin{aligned} d\vec l = dl(\sin\theta\hat x + \cos\theta \hat y)\end{aligned}$$ Así, la fuerza infinitesimal en esa sección de alambre viene dada por: $$\begin{aligned} d\vec F &= I d\vec l \times \vec B = I dl(\sin\theta\hat x + \cos\theta \hat y)\times (-B\hat z)\\ &=-IBdl (\sin\theta\hat x \times \hat z + \cos\theta \hat y \times \hat z)\\ &=-IBdl (-\sin\theta \hat y + \cos\theta\hat x) \\ &= IBdl\sin\theta \hat y - IBdL\cos\theta \hat x = dF_y\hat y + dF_x \hat x\end{aligned}$$ donde, en la última línea, escribimos explícitamente el$y$ componente$x$ y del vector de fuerza infinitesimal. Para sumar estas fuerzas infinitesimales, lo más conveniente es usar el ángulo$\theta$ para identificar cada segmento. $d\theta$se relaciona con$dl$, ya que$dl$ es la longitud del círculo subtendida por el ángulo infinitesimal$d\theta$: $$\begin{aligned} dl = Rd\theta\end{aligned}$$ Sumando todos los$y$ componentes de las fuerzas infinitesimales: $$\begin{aligned} F_y = \int dF_y = \int_0^\pi IBR\sin\theta d\theta=IBR \int_0^\pi\sin\theta d\theta=2IBR\end{aligned}$$ Tenga en cuenta que los$x$ componentes suman a cero, como predijimos a partir de $$\begin{aligned} F_x = \int dF_x = -\int_0^\pi IBR\cos\theta d\theta=-IBR \int_0^\pi\cos\theta d\theta=0\end{aligned}$$ la simetría: La fuerza neta en el alambre viene dada por: $$\begin{aligned} \vec F = 2IBR\hat y\end{aligned}$$

Discusión:

En este ejemplo encontramos la fuerza magnética en una sección curva de alambre portador de corriente. El cálculo fue simplificado por argumentos de simetría, ya que podríamos usar la regla de la mano derecha para anticipar que la fuerza no tendría ningún componente en la$x$ dirección. Esto se debe a que hay tanta corriente fluyendo en la$y$ dirección positiva como hay en la$y$ dirección negativa, de manera que las fuerzas correspondientes cancelan. Sin embargo, hay un flujo neto de cargas en la$x$ dirección positiva, lo que lleva a una fuerza neta en la$y$ dirección positiva. Como corolario, la fuerza magnética neta en cualquier bucle cerrado de corriente debe ser cero.